基于反褶积广义S变换的流度属性提取方法在潜山储层预测中的应用

兰昀霖 , 文晓涛, 张超铭, 何易龙, 王锦涛

(成都理工大学 a.油气藏地质及开发工程国家重点实验室，b.地球物理学院，成都 610059)

0 引言

近年来，在高青、埕岛、车镇等地区古生界潜山风化壳中上百万吨产能油井的发现，表明潜山仍蕴含着较大的勘探潜力，潜山已成为重要的增储方向。草桥古潜山构造带位于山东省广饶县大营乡境内，北部为牛庄洼陷，南邻牛头镇洼陷，西接乐安油田，东北部为八面河油田，储层埋藏深度小于1 000 m，属于碳酸盐岩孔隙、裂缝、溶洞复合型油藏，具有油水性质复杂多变、储集空间多种多样的特点，多口完钻井均有良好的油气显示。该研究区属角度不整合型风化壳输导体系，即风化壳上的地层与风化层下的地层间呈角度不整合接触。上覆地层由北至南依次为孔店组—沙四段、馆陶组、明化镇组，形成如图1所示的复杂潜山披覆构造带。受风化、淋滤、溶蚀作用影响，古潜山下伏碳酸盐岩层的孔隙度和渗透率变大，能够形成裂隙或溶洞，成为油气聚集的空间。古岩溶剖面结构的垂向和侧向非均质性强，不同结构层的输导能力、储集物性差异明显，这种差异可能影响和控制输导体系中油气的运移和聚集。但是目前对风化壳古岩溶带结构缺少系统和精细地刻画，钻井资料显示，该地区潜山内幕地层划分和比对困难，成藏条件及油藏类型相当复杂，储层物性纵、横向变化大，成藏规律不易弄清；试油资料初步显示，岩性风动中的含油性差别较大，含油与含水情况不一。原油分析的相对密度、粘度受构造部位、埋藏深度的影响较大，表明油水关系和油水性质比较复杂[1]。为了更好地反映该储层的物性及其流体流动性，引入流度属性这一指标。流度属性是渗流力学中的概念，表示流体流动的难易程度，流度属性越大，表明流体流动性越强，能够为油气预测和勘探等提供帮助。Silin等[2]推导获得低频域中流体饱和多孔介质中地震信号反射系数的简化渐进表示；代双和等[3]首次利用流度属性预测优质储层集，在不依赖解释层位的条件下仍能得到准确预测结果；蔡涵鹏等[4]从实际生产的角度研究了低频振幅和流体流度属性的关系，并得到验证；陈学华等[5]将利用广义S变换计算瞬时地震谱的方法应用到流度属性计算中，通过纵波反射理论公式确定优势频率，结合流度属性来达到解释储层的含油气性的目的；张生强等[6]利用基于高分辨率反演谱分解的流体流度计算，得到的剖面具有高分辨率的特点，且能在无井的情况下进行定性分析，减少了流体识别中的多解性和不确定性；张懿疆等[7]通过反褶积广义S变换研究薄储层的低频阴影，克服了传统固定时窗的局限，得到更高的时频分辨率；杨吉鑫等[8]将稀疏自适应S变换应用到海上地震资料的流度属性计算，得到较高分辨率的储层流度显示，同时能有效克服测不准原理的影响。笔者将基于反褶积广义S变换的流体流度属性提取方法应用在草桥古潜山油藏储层，结果表明该方法不仅能够精确预测出含油层，还有效提高了流度属性剖面的分辨率，为该区域油藏储层的勘探开发提供有力依据。

图1 A1井——A7井南北向油藏剖面图Fig.1 Profile of N-S reservoir in well A1-A7

地震频谱分辨率的高低，取决于所选时频分析方法的优劣[9]，①短时傅里叶变换通过选取固定的窗函数进行变换，通常适用于平稳或近似平稳信号，但无法同时满足频率和时间分辨率的要求，且会受到测不准原理的限制；②小波变换在短时傅里叶变换的基础上采用长度变化的时窗来变换信号，可以更好地分析局部频率特征，但也具有和短时傅里叶变换同样的缺点[10]；③广义S变换的时频窗口能根据频率尺度自适应进行调整，具有更高的灵活性和适用性，但仍受到测不准原理的制约[11]；④Wigner-Ville分布避免了时频分辨率的相互牵制，具有更好的时频聚集性，但分析多分量信号时会受到交叉项的干扰[12]。⑤反褶积广义S变换是基于反褶积短时傅里叶变换提出的，保留了广义S变换优点的同时也有效避免了其缺点,该方法能够自适应地调整时窗，在处理非平稳地震信号时仍有较高的时频分辨率。

笔者通过仿真实验比较多种时频分析方法验证反褶积广义S变换为最优法，采用基于该方法的流体流度属性提取方法应用在草桥古潜山油藏储层，并通过实际应用验证了该方法的有效性，为该地区的油藏勘探开发提供有力依据。

1 方法原理

1.1 流体流度属性

Silin推导的平面纵波反射系数R在某个角频率ω下的渐进表达式为式(1)。

(1)

式中：i是虚数单位；R0和R1是和孔隙度、密度、弹性系数相关的流体和岩石力学性质的无量纲参数；ρb是流体密度；k是相流体有效渗透率；η是流体粘滞系数；ω是地震波角频率。

对式(1)中的ω求导，得式(2)。

(2)

再令

(3)

Golohubin在低频渐进分析理论的基础上提出成像属性，即：

(4)

式中，dS(ωlow)是地震频谱。通过式(2)和式(4)可得式(5)，式(5)表明流度属性能够反映储层的渗透率，C是一个与多孔岩石系数有关的复函数，可以通过岩石物理测试得到[13]：

(5)

流体流度属性定义为式(6)。

M=k/η

(6)

通过式(6)可以看出，储层的渗透率越好，其所含的流体粘滞系数越低，则储层中流体的活动能力越大，含油气的可能性就越大。利用式(6)和式(5)改造对比，能够直观地反映储层所含流体的活动能力，由式(5)和式(6)可得式(7)。

(7)

时频分析中，将原始信号与窗函数各自的时频谱进行二维褶积能得到某一变换方法的变换谱，所以当已知该变换方法的频谱和窗函数的时频谱时，就能通过反褶积得到原始信号的时频分布[7]。

2.2 反褶积广义S变换原理

对信号x(t)做广义S变换，得到广义S变换谱：

式中：τ是时间位移；f是频率；高斯窗调节参数λ>0,p>0。

广义S变换谱为(原始信号的Wigner-Ville分布和高斯窗的Wigner-Ville分布的二维褶积)：

Wh(t-u,f-v)dudv

(9)

其中：Wx为原始信号x(t)的Wigner-Ville分布；Wh为高斯窗h(u)的Wigner-Ville分布。

将得到的广义S变换谱代入反褶积算法中，反褶积算法表达式为式(10)。

(10)

假设广义S变换谱和高斯窗的Wigner-Ville分布做褶积得到A1，广义S变换谱与A1的比值为B，B与高斯窗Wigner-Ville分布相关得到A2，将A2与广义S变换谱褶积得到新的A1，通过反复的迭代计算即可得到原始信号的时频分布A2。

WVD本质上是信号在时频面上的能量分布。如果信号是由两个分量组成，即：

x(t)=x1(t)+x2(t)

(11)

则Wigner-Ville分布

WVD11(t,f)+WVD22(t,f)+

WVD12(t,f)+WVD21(t,f)

(12)

式(12)是信号的交叉项，末尾两项是相等的分量，分量越多，表明信号的交叉项越多，从而影响信号的识别[13]。

通过上述对反褶积广义S变换和Wigner-Ville分布的描述可知，Wigner-Ville分布在处理地震信号这类典型非平稳信号时会产生交叉项，而通过对广义S变换进行反褶积处理能够有效地抑制这些分量，即交叉项的产生，从而提高信号识别的准确度[7]。基于反褶积广义S变换的流度属性计算流程图见图2。在流程中，影响效果的关键因素是时频分析方法的选取，适合的时频分析方法能够得到高分辨率、高汇聚度的剖面，反之则会大大降低剖面的成像能力，影响我们对其中信息的分析及判断。陈学华等[14]改造广义S变换的高斯窗函数，引入两个调节因子，使其具有更高的灵活性和时频分辨率。在仿真分析中，调节因子是影响分辨率及汇聚度的关键因素。

图2 基于反褶积广义S变换的流度属性计算流程图Fig.2 Flowchart of calculating mobility attributes based on deconvolution generalized S transform

2 仿真分析

首先利用合成信号，分别得到短时傅里叶变换、广义S变换、反褶积短时傅里叶变换和反褶积广义S变换的时频分析结果，并进行比较分析，以选取合适的时频分析方法。合成信号x(t)是由三个时变信号叠加而成：

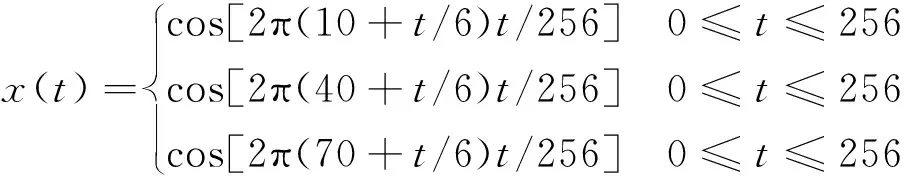
(13)

图3为合成信号，由3个倾斜的平行线性信号组成，可以模拟实际地震资料中的薄互层[15]。由于地震子波带限引起的薄互层调谐影响是地震资料中不可避免的缺陷[16]，这种缺陷常给信号分析带来严重的干扰，因此可通过对薄层识别的效果好坏来判别时频分析方法的优劣。

图3 仿真信号Fig.3 Original signal

图4(a)为对该信号做短时傅里叶变换得到的时频分布图，分辨率整体上较低，信号层之间干扰严重，且受到短时傅里叶变换固定时窗的影响，信号低频和高频部分两端(红色矩形框内)均有轻微延伸现象。图4(b)为对该信号做广义S变换得到的时频分布图，整体分辨率和图4(a)相当，且仍受到层与层之间调谐作用的影响，但相比于图4(a)不存在两端信号拉伸现象。图4(c)为对该信号做反褶积短时傅里叶变换得到的时频分布图，具有较高的时频分辨率，但能量较弱，且低频部分首端(红色矩形框内)有缺失。图4(d)为对该信号做反褶积广义S变换得到的时频分布图，具有较高的时频分辨率，且不存在层间调谐作用。将以上四种时频分析方法对信号处理的结果进行对比可知，反褶积广义S变换的时频谱相较于短时傅里叶变换、广义S变换、反褶积短时傅里叶变换等具有较高的分辨率和频率汇聚度，且有效克服了傅里叶变换固定时窗的局限性，避免了薄层之间的调谐效应。适用于处理实际地震资料中的非平稳信号，故采用基于反褶积广义S变换的流度属性提取方法,在理论上具有较高的适用性和有效性。

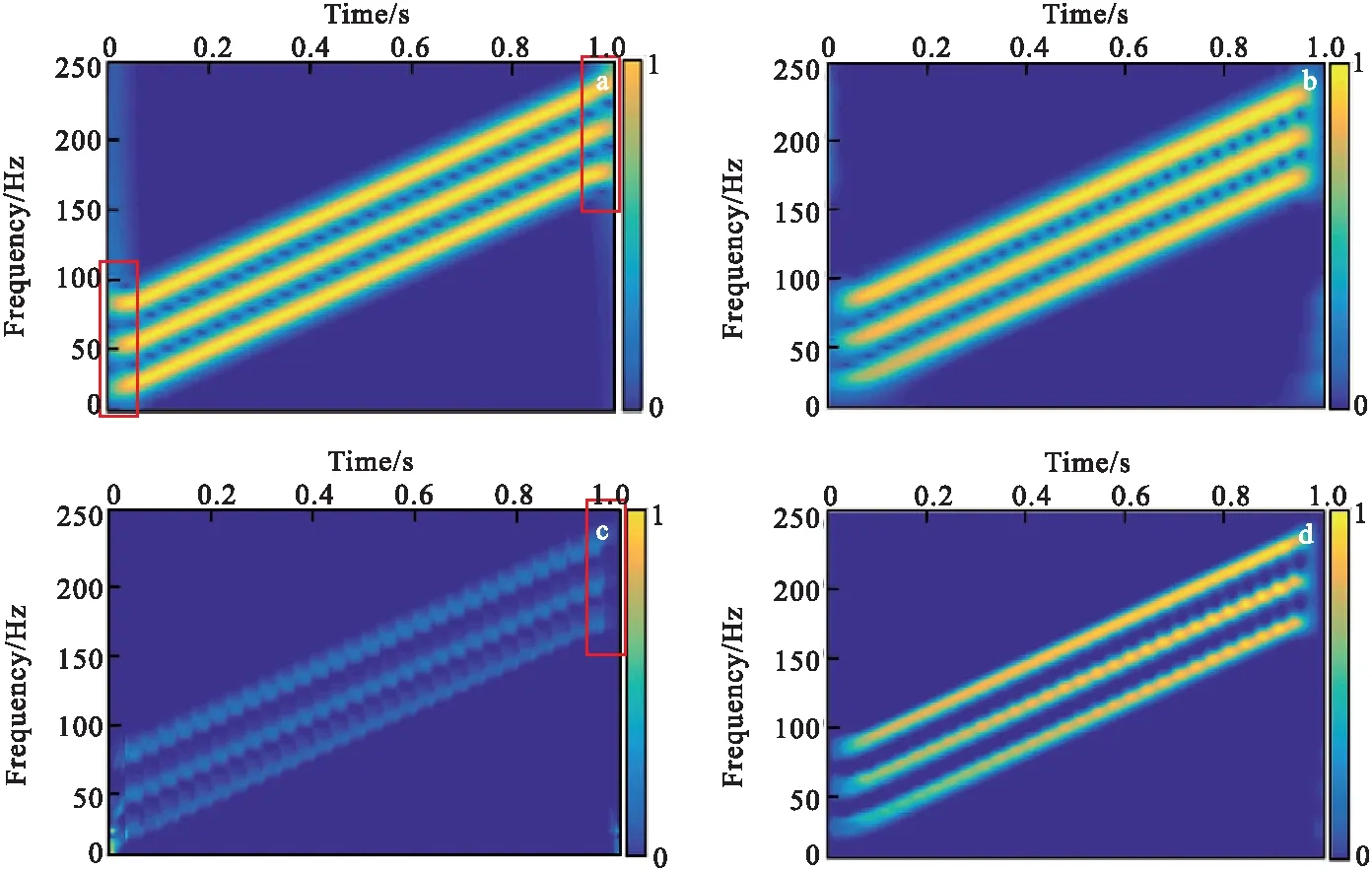
图4 不同分析方法得到的时频谱Fig.4 Time spectrum obtained by different analysis methods(a)短时傅里叶变换时频谱;(b)广义S变换时频谱;(c)反褶积短时傅里叶变换时频谱;(d)反褶积广义S变换时频谱

图5为潜山模拟储层模型，图5(b)为采用分步傅里叶法[17]正演模拟的结果，如图5所示，基于反褶积广义S变换得到的储层流体流度属性剖面中目的层的高流度值区域与图5(a)中储层位置对应较好，且储层上半部分流度值较高，验证了该方法的有效性及适用性。该储层具有较强的衰减，储层下界面同相轴能力减弱，流度下界面不敏感，上界面敏感。流度属性较高的位置表明该区域位置储层物性较好，存在含油气的可能性较大。图5中模型考虑的是储层速度较大的情况，为了进一步从模型上显示不同储层参数的情况，并论证该方法的适用性，现探讨另一种情况。综合考虑孔隙度等参数的影响，如孔隙度变大，即孔隙空间体积比值变大，渗透率高，则该层的速度将减小。在图6模型中适当减小目的储层的速度，以模拟不同参数条件下的情况。从图6可以看出，与图5中储层模型类似，图6(c)中目的层的高流度值区域和图6(a)中储层位置对应较好，进一步验证了该方法的适用性。

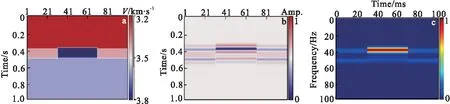
图5 储层模型Fig.5 Reservoir model(a)地质模型;(b)合成地震记录;(c)反褶积广义S变换得到的流度属性

图6 储层模型Fig.6 Reservoir model(a)地质模型;(b)合成地震记录;(c)反褶积广义S变换得到的流度属性

3 实际应用

为进一步验证文中基于反褶积广义S变换的流体流度属性提取方法，在实际工区的正确性和有效性，从草桥古潜山的地震数据中提取了流度属性。该区属碳酸盐岩孔隙裂缝-溶蚀型复合油藏，进山深度为520 m～840 m，原油密度为0.98 g/cm3，粘度为28 500 Pa·s～65 000 mPa·s[1]，顶面埋藏深度为600 m～976 m，潜山地层倾角为10.4°～44.0°，多口完钻井均有良好的油气显示，具有一定的实际勘探意义和价值。

图7为A-B-C-D-E-F井连井地震剖面，在剖面上馆陶组与下马家沟组间的风化壳界面特别清晰。图8为地震频谱图，从图8可知，地震主频为25 Hz左右。图9为其对应的流度属性剖面，从剖面上来看，整个风化壳的流度属性总体较高，但在侧面上表现出明显的非均质性，常出现高流度属性区与低流度属性区相间的现象，表明侧向流通性较差。红色矩形中的区域流度属性较高，表明该区域位置储层物性较好，存在油气的可能性较大。图10是对应流度属性剖面的频谱图，振幅曲线主要在低频部分显示。

图7 过A-B-C-D-E-F井连井地震剖面Fig.7 Well seismic section

图8 地震频谱图Fig.8 Seismic spectrogram

图9 反褶积广义S变换获得的流体流度属性剖面Fig.9 Fluid mobility profile obtained by deconvolution of generalized S-transform

图10 地震频谱图Fig.10 Seismic spectrogram

图11、图12、图13分别是井A、井B、井C的流度属性剖面及其岩溶旋回解释图。将过井流度属性与相应测井解释结果对比分析，说明应用流度属性预测储层流体流动的合理性。

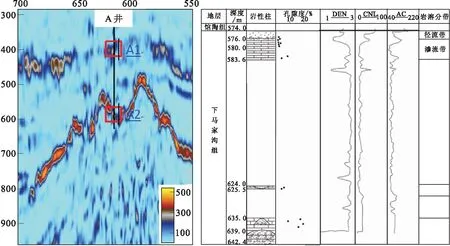
图11 过井A的井流度属性剖面及岩溶旋回解释图Fig.11 Flow property profile and karst cycle interpretation map of well A

图12 过井B的井流度属性剖面及岩溶旋回解释图Fig.12 Flow property profile and karst cycle interpretation map of well B

图11、图12、图13中的矩形框分别对应各自的渗流带。图11中目的井A处于草古某潜山北部较低部位，实钻证实，该井目的层奥陶系储层发育，物性好。钻遇地层自574 m到642 m，储集层厚度为68 m，占钻遇地层的100%，综合解释为油水同层。红色矩形框A1对应右图中渗流带和径流带，矩形框A2对应右图潜流带，总体流度属性呈高值，说明该处流体流动性较好，与实际解释符合；图12中目的井B是处于潜山构造带东部较高部位的一口评价井，从528 m到585 m属馆陶组，钻遇地层厚度57 m，从585 m到645 m属奥陶系，钻遇地层厚度60 m，见到了一定的油气显示。图12中红色矩形内流度属性呈高值，说明该处的流体流动性好，存在油气的可能性大，与实际相符合；目的井C是位于潜山北高点的一口评价井，该区含油层位均在奥陶系地层，而寒武系地层是区域奥陶系地层的遮挡层，加之岩心裂缝不发育，不具备储集空间，所以无油气充注。图13中红色矩形内流度属性呈低值，对应地层综合解释为干层，与实际符合。通过流度属性与实际钻井、测井和试油的对比表明，流度属性能较好地反映流体在风化壳中的输导性能。

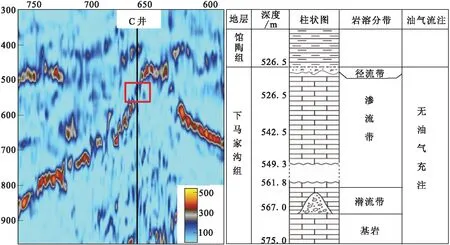
图13 过井C的井流度属性剖面及其岩溶旋回解释图Fig.13 Flow property profile and karst cycle interpretation map of well C

对过井的流度剖面和相应测井解释结果(井A、井B、井C)对比分析(表1)可知，井旁流度属性有显示的时间厚度，通过速度转换成预测厚度后，与测井解释结果的真实厚度能够较好地对应，且测井解释储层厚度或有油水充注厚度厚的地方，相应地在流度属性上也表现出流度属性好的厚度较厚，这表明应用本方法预测储层流体流动性的趋势是可行的。

表1 由流度估算的储层厚度Tab.1 Reservoir thickness estimated by mobility

4 结论

计算地震数据的瞬时振幅谱是流度属性计算过程中不可或缺的一步。流度属性剖面的分辨率高低取决于时频分析方法的优劣，故时频分析方法的选取对于储层预测的精度有较大的影响。与短时傅里叶变换、反褶积短时傅里叶变换、广义S变换等时频方法相比，反褶积广义S变换具有频率高、聚集性好、自适应性强的特点，且能有效避免调谐作用，因此为较好的一种时频分析方法。笔者将基于反褶积广义S变换的流度属性提取方法应用到草桥古潜山地区，通过多个过井流度剖面及岩溶旋回解释图验证了预测的正确性和准确度，同时提高了流度属性剖面的分辨率，较好地反映了该潜山目的储层处的流体流动性特征，为之后进一步的油藏勘探开发工作提供有力支持。