“双减”背景下小学数学复习课结构化教学策略初探

文/刘小燕

引言

复习是数学课堂教学必不可少的环节，有利于学生巩固知识和提升技能，提高应用知识解决问题的能力，对学生的数学学习起着不可替代的作用[1]。但在实际的小学数学复习课中，部分教师习惯以讲评、操练式的习题教学为主，意在提高学生的解题能力，使学生获得更好的学习成绩，但这一方式无法激发学生复习的兴趣。数学知识具有逻辑性、关联性、系统性的特点，教师应采用结构化教学的方式进行数学复习课教学，以整体关联为抓手，以动态建构为核心，以发展思维为导向，以促进学生能力与素养的提升为目标，以期在减轻学生负担的同时，提高教学质效，促进学生的全面发展。

一、经历梳理过程、积累复习经验——习得“法”

结构化教学强调“授学生以渔”，方法比知识更重要。著名教师林良富曾说：“新授课好比获得一颗颗‘珍珠’，而复习课犹如将闪闪发光的‘珍珠’串起来。”复习课不仅要复习梳理学科知识，将“珍珠”串成“项链”，做到从“温故”到“知新”，还应该放手让学生经历自主复习的过程，积累复习整理的经验，逐渐习得复习整理的方法，做到从“串珠”到“悟道”[2]。

（一）整理已有认知，梳理知识结构

以苏教版数学三年级（下册）“长方形和正方形周长与面积的复习”为例，教师打破时间的限制，在课前放手让学生用自己喜欢的方式将相关知识进行整理，让每位学生都有充裕的时间去收集、归纳、整理所学知识，带着自己的思考进入课堂。学生在小组内分享自己课前的单元整理，互相提出改进的建议，并在班级进行交流。由于教师给学生搭建了充分展示个性思维的平台，学生的方法也精彩纷呈，具体如下所述。

生1：周长与面积含义不同，长方形周长是指一周边线的长，也就是四条边的和，而面积是指面的大小。

生2：周长和面积计算方法也不同，可以举例计算来进行区别。

生3：可以列表（见表1）或思维导图。

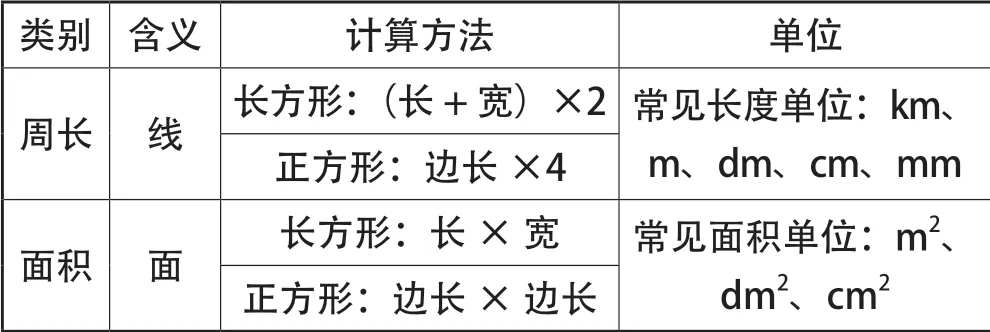
表1

学生从已有的经验出发，用描述、画图、举例、编顺口溜、列表和思维导图等形式，初步尝试对周长与面积的知识进行个性化的梳理、归纳、整合，然后小组互相分享、全班交流，相互提出修改建议并进行评价。在这个过程中，学生不但发现了长方形和正方形的周长和面积含义不同、计算方法不同、单位不同，将碎片化的知识进行整体结构的构建，而且不断丰富、优化了自己的复习整理结果和整理方法，积累了多种复习整理的经验[3]。

（二）解决存在困惑，促进自我提升

长方形周长与面积复习课课前整理单的设计，除了可以让学生梳理相关知识，还应引导学生反思记录自己在本单元学习中仍存在的困惑，进而释疑解疑，及时查缺补漏。学生课前反思并提出了这些很有价值的思考：“周长和面积有什么区别和联系？周长相等的图形面积相等吗？周长相等的图形，什么形状面积会最大呢？”教师将学生的疑问进行筛选和整合，再有针对性地引导学生进行探究，从而使复习过程更有的放矢，同时培养学生质疑反思的习惯。

（三）分析错例成因，学会举一反三

皮亚杰说过：“学习是一个不断犯错误的过程，同时又是一个不断通过反复思考导致错误的缘由并逐渐清除错误的过程。”本节复习课，教师还可以让学生收集平时解决长方形周长和面积问题的错例，与小组的同学辨析交流，追根溯源，明晰知识盲点，实现知识的再学习、思想方法的再应用，以错明真、以反求正，提高举一反三、知识迁移的能力。

二、横向重组练习，串联点状知识——连成“线”

虽然练习巩固是复习教学中不可或缺的一部分，但教师不能将复习课和习题课、练习课划上等号，应注重对教材习题背后的意图进行准确解读与分类整理，并结合学生本单元存在的学习困惑，横向重组练习，提炼出核心问题，将点状的知识连成“线”、串成“片”，让学生能更轻松地复习，达到减负增效的教学目标。

（一）横向整合练习，提炼核心问题

“长方形和正方形周长与面积的复习”是学习完“长方形面积”这单元内容后的一次系统复习，教材一共安排了13 道习题。通过认真解读教材不难发现，教材中的这些练习的编写旨在复习对比周长和面积的含义、单位及计算方法，考查学生在具体生活情境中对周长和面积的辨析与简单应用，通过图形的变化和比较，进一步让学生体会周长和面积的区别。教师如果照本宣科地让学生做习题，不仅会让学生感到索然无味，还会因为练习多、情境杂而无法使学生体会到知识间的内在联系。因此，笔者对这些习题进行重组整合，抓住周长和面积概念的对比和图形的变化，化繁为简，提炼以下三个问题，深化学生对周长与面积概念的认知，同时提高复习的实效性、趣味性、挑战性。

问题一：边长是4dm 的正方形，周长和面积相等吗？

周长和面积是两个极易混淆的概念。学生虽然通过课前的自主整理与课始的汇报交流，了解了周长与面积的区别，但是对此的理解仅仅停留于表面，在特定情境下易受到干扰。有的学生认为相等，因为这个图形的周长和面积列式都是4×4=16。有的学生从概念的本质出发，认为不相等，因为周长和面积的含义不同，周长是一条线，面积是一个面，周长和面积的单位也不相同。正方形周长是边长×4，面积是边长×边长。本环节辨析4×4 的正方形周长和面积是否相等，学生在独立思考、辨析交流和课件的直观演示中，从不同的角度比较，不仅加深了对周长和面积概念本质区别的认识，还进一步理解了周长与面积的计算原理。

问题二：周长相等的图形，面积相等吗？

生1：“通过举例（见表2），我发现周长相等的图形，面积（不一定）相等。”

表2 研究记录单

生2：“通过举例（如图1），我发现周长相等的图形，面积（不一定）相等。”

图1

生3：“通过举例（如图2），我发现周长相等的图形，面积（不一定）相等。”

图2

问题三：面积相等的图形，周长相等吗？图3 中的小方块周长相等吗？如果再增加1 个小方块，和原来比，周长变不变？

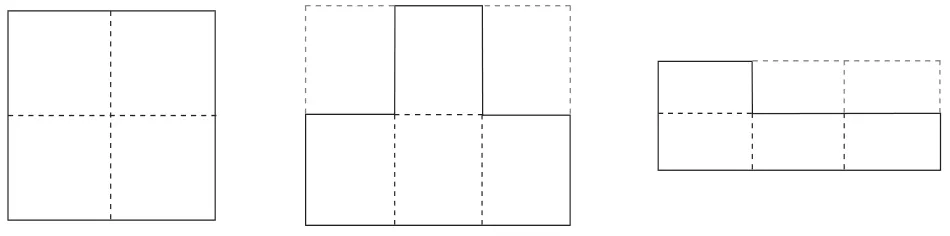
图3

本环节通过将习题进行有效重组，以学生熟悉的、丰富多变的俄罗斯方块为探究素材，紧扣图形变化中的“变与不变”，引导学生自主提出猜想、举例验证猜想，不仅激发了学生的探究兴趣，使学生体会到面积相等的图形周长不一定相等、周长相等的图形面积不一定相等，还渗透了“变与不变”的数学思想和“猜想验证”的科学方法，培养了学生严谨务实的理性精神[6]。

（二）提供基本条件，多维自编习题

以“长方体和正方体体积的复习”一课为例，教师打破了“教师出题、学生解题”的常规，只提供给学生一个基本条件，让学生自主编题解题。

师：“如果这是一个鱼缸，长50dm、宽30dm、高30dm，不增加任何条件，你可以提出什么问题？”

生：“鱼缸的占地面积是多少？这个无盖鱼缸的表面积是多少？鱼缸的体积是多少？”

师：“如果允许你增加一个条件，你能提出其他问题吗？”

生：“鱼缸的水深如果是5dm，水的体积是多少？如果水深5dm，水和玻璃接触的面积是多少？倒入32L的水，水面高多少dm？”

教师搭建这样富有张力、激发创新的平台，能促进学生对已有的长方形或长方体周长、面积、表面积、体积知识进行深度加工，从多维度沟通知识间的联系。

三、纵向沟通关联、寻求知识本源——构成“体”

数学知识不是一个个孤立的存在，知识与知识之间有着严谨的结构与千丝万缕的联系。结构化教学强调教师在教学中要引导学生沟通知识之间的前后联系，建立起知识脉络和整体架构，完成知识的迁移，要用系统的眼光和结构化的意识进行复习课教学。

例如，在教学苏教版数学三年级（下册）“长方形和正方形周长与面积的复习”时，教师引导学生对比辨析4×4 的正方形周长与面积的区别，启发学生思考：“周长和面积计算有什么联系呢？”学生在具体实例和课件的直观演示中，初步感受到计算周长是在计算含有几个长度单位，计算面积是在计算含有几个面积单位，它们都是在计算含有几个计量单位，从而沟通了概念的联系，感受到度量的本质。又如，在“多边形的面积”这一单元中有“等底等高”这一知识点，学生虽对此有一定的了解，但是对其本质意义还不是完全清楚。针对这一问题，教师可以设计问题：“在完全相同的三个平行四边形里分别突出了不同形状的阴影（如图4、图5、图6）。现在想知道哪一幅图中的阴影面积最大，你们有什么好的办法吗？”并留给学生交流讨论的时间。学生根据“等底等高”和画辅助线得出图4 和图5 的阴影面积是平行四边形面积的-。教师继续提问：“如果像这样的方法涂出更多的三角形，那么阴影面积的和还是平行四面形面积的-吗？”学生在教师的引导和自己的观察下发现：从而明白只要三角形的底边之和等于平行面积的底，高等于平行面积的高，那么阴影三角形面积之和就是平行四边形面积的-。通过这样的方法，学生的认知结构得到了深化。

图5

图6

四、贴合生活实践、提升综合能力——促进“思”

教学的最终目的是使学生能将所学所得运用在实际生活中。因此，教师要立足学生已有的认知基础，通过将数学问题与生活问题进行适当的改编，唤醒他们丰富的生活经验，创设富有张力的问题情境。这样不仅能提高学生综合应用知识的能力，使其感受到数学与生活的关联，促使学生的思维逐步发展，还能帮助学生更好地理解数学，卸下心理上的负担，是另一种意义上的减负增效。

例如，在教学“长方形和正方形周长与面积的复习”时，教师可以设计一道开放性的作业：“王大爷如果用12m 长的木栅栏围一个长方形的鸡舍，怎么围面积最大？”这道生活实际问题，很好地发散了学生的思维，也会使学生的视野越来越开阔、思维越来越深刻。

结语

综上所述，结构化视角下的小学数学复习教学，不仅能提高教师教学的质效、学生学习的质效，还能减轻学生身体和心理上的负担，实现减负增效的教育目标。教师应用系统的眼光、结构化的意识、整体的思想进行结构化复习课教学，优化复习教学的流程，以此更好地帮助学生形成知识结构、认知结构，推动学生核心素养与综合能力的全面提升，从而与学生共同成长。