钢包钢管混凝土防护门动力响应及其影响因素分析

江中正，孙善政，卢 浩，岳松林

(陆军工程大学 爆炸冲击防灾减灾国家重点实验室， 南京 210007)

1 引言

随着武器威力不断提高和精确制导技术的广泛使用，防护工程面临的威胁越来越大。尤其是近几年，在不断有新式常规武器被研发成功并列装到军队的形势下，防护工程需要有针对性地提高自身防护能力。对工程口部重要的防护设施——防护门开展设计研究，一直以来是防护工程的重点。为满足现实改善防护门厚重，提高抗力等需求，近年来主要从以下方面做出努力：一是结合试验数据，在数值软件中对防护门进行数值分析，对门体结构体系和形式进行优化；二是使用新的门扇材料或填充材料，达到提高防护门性能的目的。钢包钢管混凝土这种结构形式充分利用了钢管混凝土高弹高塑的优势，具有承载力高、刚度大、韧性好的特点；张湘冀等利用数值分析软件检验了一种全封闭的钢—混凝土—钢夹层板的抗暴性能，结果表明该结构具有良好的抗爆性。石少卿等把箱型钢板添加到了钢筋混凝土板中，增强对内部混凝土的约束，极大地提高了钢筋混凝土板的承载力；方秦等在试验中为提高防护门抗力，将弹性与阻尼支承安装到防护门两端，并采用理论和数值模拟相结合的方式对平板式和拱型钢包混凝土高抗力防护门的动力响应进行，分析表明设置弹性与阻尼支承可使防护门的承载力显著提高，荷载作用时间越短，抗力提升的效果越明显。随着数值分析能力和计算机技术的发展，数值模拟已成为研究爆炸这类高度非线性问题的重要方法。Hsieh 等在研究在爆炸荷载作用下不同尺寸梁板式防护门的动力响应特征时，利用有限元程序进行了数值模拟，结果表明肋梁的分担了很大一部分爆炸荷载，其首先发生局部屈服的部位在铰页附近，增加梁的网格密度和厚度是一种提高防护门抗力的有效方式。陈力等在拱形钢包混凝土试验中，利用 AUTODYN确定了防护门上的爆炸荷载，并将单次和多次荷载作用下防护门的动力响应特征与试验进行了对比，认为防护门的动力响应主要受到门扇与门框的非线性接触和应变率效应的影响；郭东利用ABAQUS研究了钢包钢管混凝土在爆炸作用下的动力响应特征，分析认为在钢包钢管混凝土防护门内部的钢管对增加结构抗力贡献很大，而只增加钢管壁厚度和填充混凝土强度的作用不明显。

对于防护门的设计及评估，目前通常采用按照弹性或弹塑性状态将爆炸荷载转化为等效静载的方法计算，其中，确定结构的自振频率是计算动力系数及等效静载的关键。本文将防护门简化为简支正交各向异性薄板，采用惯性矩等效方法计算两个主方向的等效抗弯刚度，按照弹性力学理论计算两个主方向的等效泊松比，基于正交各项异性薄板理论计算钢包钢管混凝土板的自振频率及动力响应，通过数值模拟证明了计算模型的可行性，对分析了钢管壁厚度和钢板厚度对结构自振频率和动力响应的影响。

2 等效刚度及自振频率计算

2.1 等效刚度计算

对于图1所示的钢包钢管混凝土结构可以视为一种周期性结构，对这种结构的等效方法有代表体元法、渐近均匀化法等。

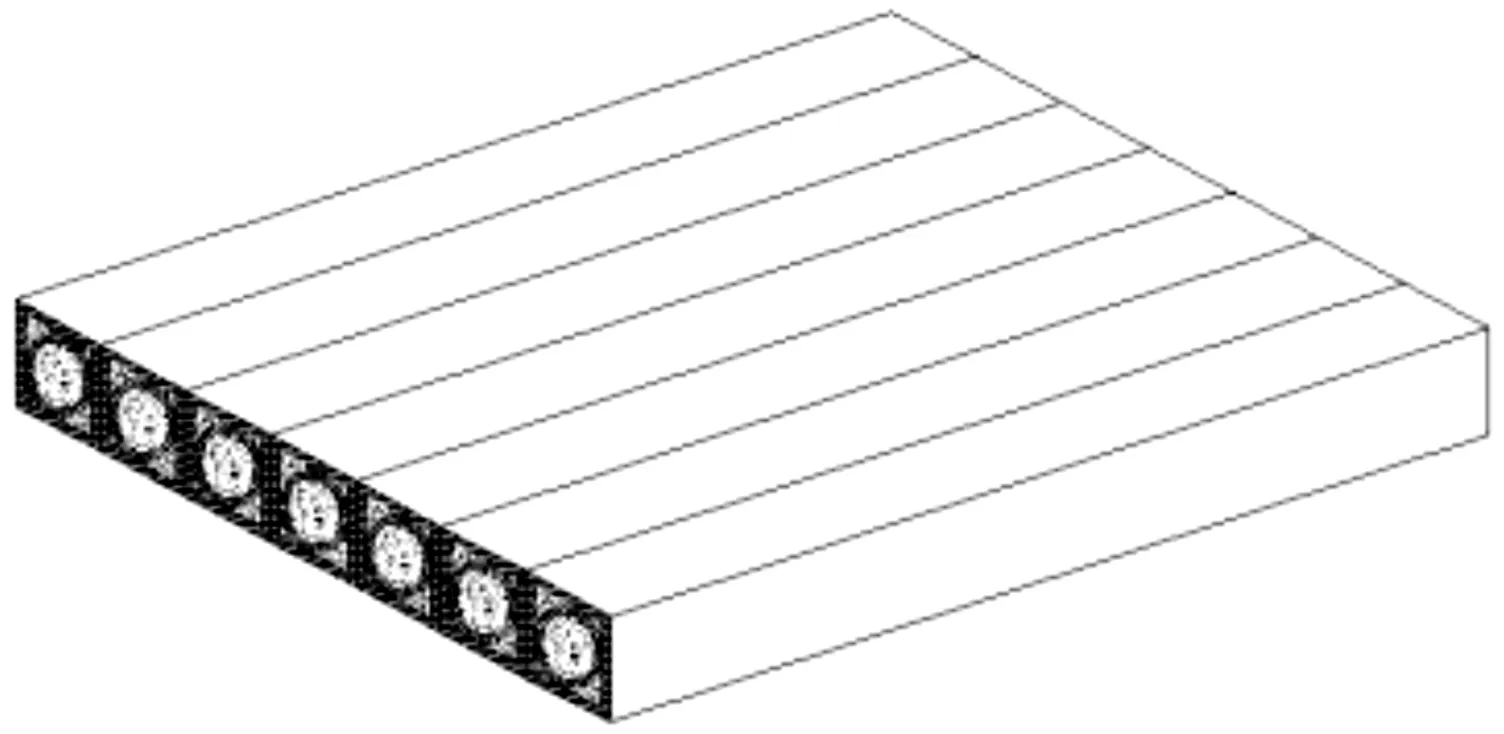
图1 钢包钢管混凝土结构示意图

参照均质平板的抗弯刚度公式(式(1))可以发现，抗弯刚度为一个单位宽度惯性矩项与材料参数项的乘积。

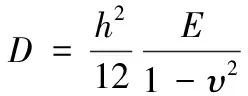
(1)

因此，钢包钢板混凝土板的等效刚度可以采用将各个材料部分截面惯性矩与材料参数相乘后在宽度方向上取平均的方法计算。

钢包钢板混凝土板模型简化过程中，垂直钢管方向忽略钢管对抗弯性能的影响，2个方向的代表体元截面图如图2。

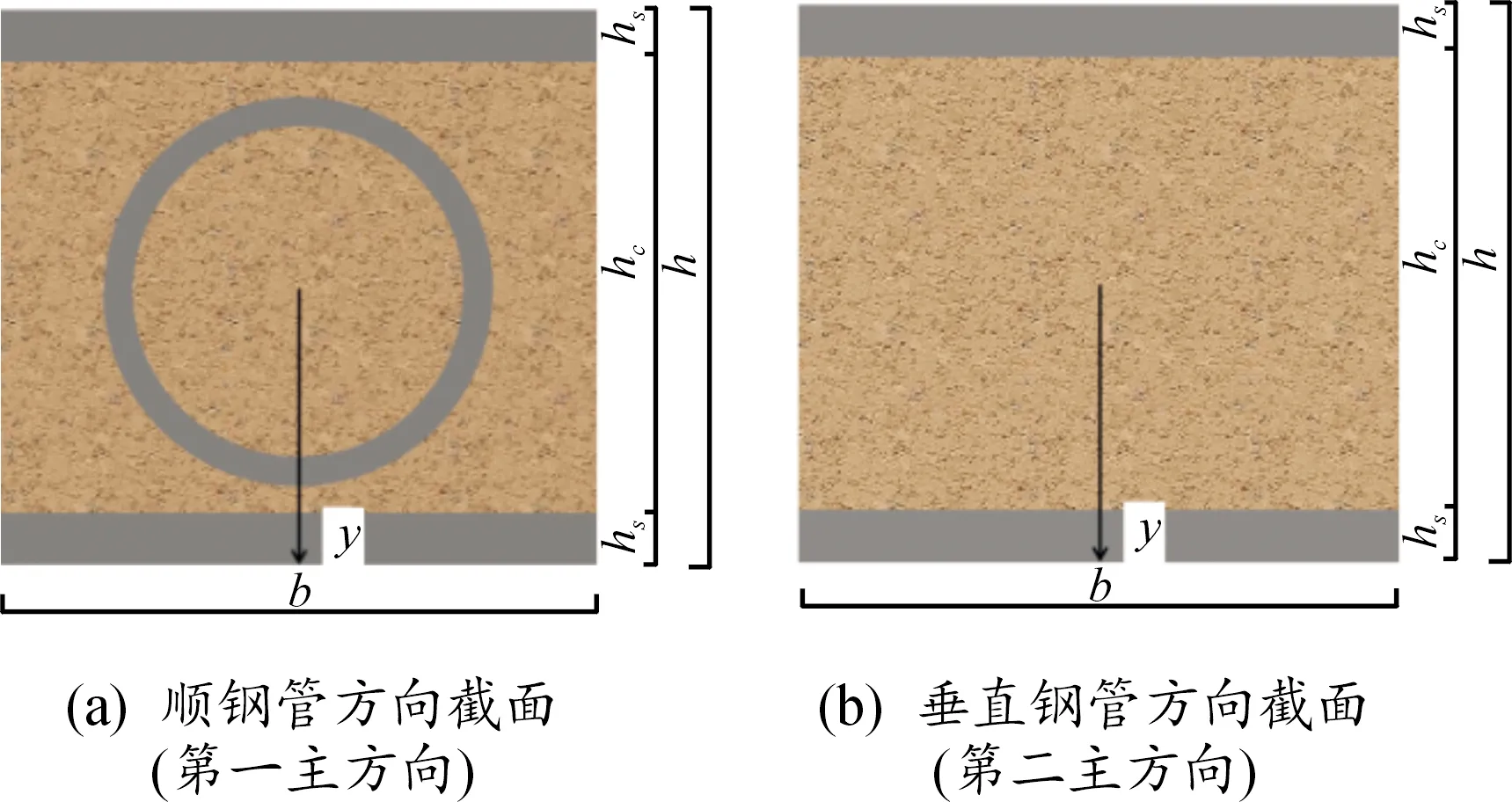
图2 钢包钢管混凝土截面图

由图2所示，2个截面的形心轴均为截面正中心处，即=0处。对于顺钢管方向，惯性矩由钢管、钢板、混凝土3个部分组成。其刚度由式(1)计算。

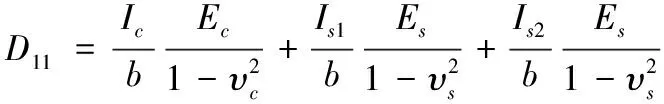
(2)

式中：为混凝土惯性矩，1为钢管惯性矩，2为钢板惯性矩，为混凝土弹性模量，为钢的弹性模量，为混凝土泊松比，为钢的泊松比。3个部分的惯性矩计算如下式所示。

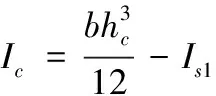
(3)

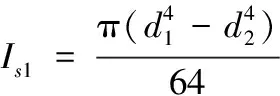
(4)

(5)

垂直钢管方向的刚度计算与顺钢管方向类似，计算过程如式(6)—式(8)所示。

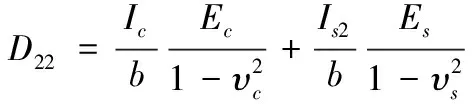
(6)

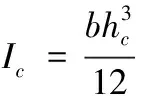
(7)

(8)

2.2 等效泊松比计算

由于圆形钢管的存在，顺钢板方向受力时垂直钢板方向的应变较难分析，但弹性阶段内垂直钢管方向受力时顺钢板方向的应变可由图2(a)结合弹性力学理论求得。首先假设钢管、钢板与混凝土协调变形。则垂直钢管方向单轴受力而顺钢管方向受力为零时可计算第一主方向上的泊松比：

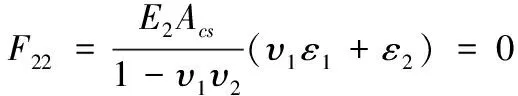
(9)

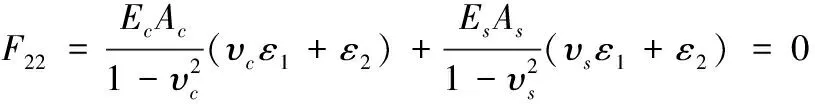
(10)

联立式(9)、式(10)得到第一主方向泊松比：

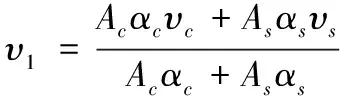
(11)

2.3 自振频率及动力响应计算

根据经典正交各项异性薄板理论，对于均布荷载，其振动微分方程为：

(12)

式中：为外荷载，为第一主方向坐标，为第一主方向坐标，为横向位移。

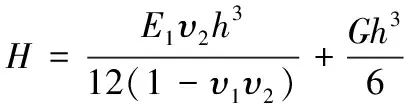
(13)

(14)

根据正交各项异性弹性力学理论，有下式所示规律。

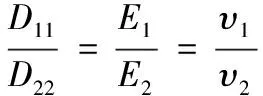
(15)

结合1.1节中计算得到的刚度比值及式(14)、式(15)，可以求解得到两个主方向的等效模量、及泊松比、。并根据式(16)得到等效剪切模量。

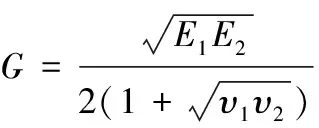
(16)

至此，微分方程(12)所需的参数全部确定。对于钢包钢管混凝土板的2个方向挠曲线形式仍假设为正弦曲线。则按照振型叠加法解微分方程，得到板中心的位移时程表达式为：

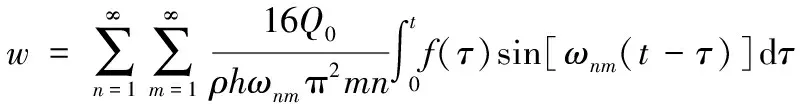
(17)

(18)

其中：为板顺钢管方向长度，为板垂直钢管方向长度，=，=，=12(1-)。

综上，对钢包钢管混凝土防护门，把结构尺寸和材料参数代入式(2)—(8)中，得到顺钢管方向和垂直钢管方向的抗弯刚度、。由式(11)、式(15)计算得到2个主方向泊松比、。由式(14)、式(15)可计算2个主方向的等效模量、。由式(13)、式(16)确定振动微分方程式[式(12)]所需的剩余参数即可得到板中心的位移时程曲线表达式[式(12)]。

2.4 算例分析

一般情况下，钢包钢管混凝土防护门是根据工程实际需要而定制的，故参考文献[7]和相关文献得到用于本文分析的防护门尺寸，顺钢管方向长度2 m，垂直钢管方向长度1.5 m，板全厚0.12 m，内包13根钢管。钢管外径0.1 m，厚度为5 mm，钢管间距0.113 m，钢板厚度5 mm。钢材采用Q235钢，弹性模量210 GPa，密度7 800 kg/m，泊松比0.22。混凝土等级为C50，密度2 700 kg/m，弹性模量为23 GPa。假设板表面均布化后峰值超压为60 kPa，正压作用时间50 ms。

由式(2)、式(6)，得到顺钢管方向和垂直钢管方向的抗弯刚度=1.294×10、=0.967×10。根据式(11)得到第一主方向泊松比=0.209，并结合式(15)得到第二主方向泊松比=0.156，运用振型叠加法求解微分方程(式(12))便可得到板的中心点位移，结果如图3所示，其中自振频率为1 079.5 Hz。

图3 位移和等效塑性应变云图

3 数值模拟分析及与理论计算的对比

3.1 模型建立

利用LS-DYNA 对钢包钢管混凝土防护门受爆炸荷载问题进行数值模拟研究，按照1.4节中的尺寸及材料参数进行建模。利用Truegrid建模软件对钢包钢管混凝土进行建模，均采用Solid168实体单元，其中钢板、混凝土、钢管的网格尺寸均为10 mm，钢板及钢管的厚度方设置为单层网格，如图4所示。模型共有57万单元。钢管、钢板与混凝土之间设置自动接触，四边通过约束节点的横向位移实现四边简支的边界条件。

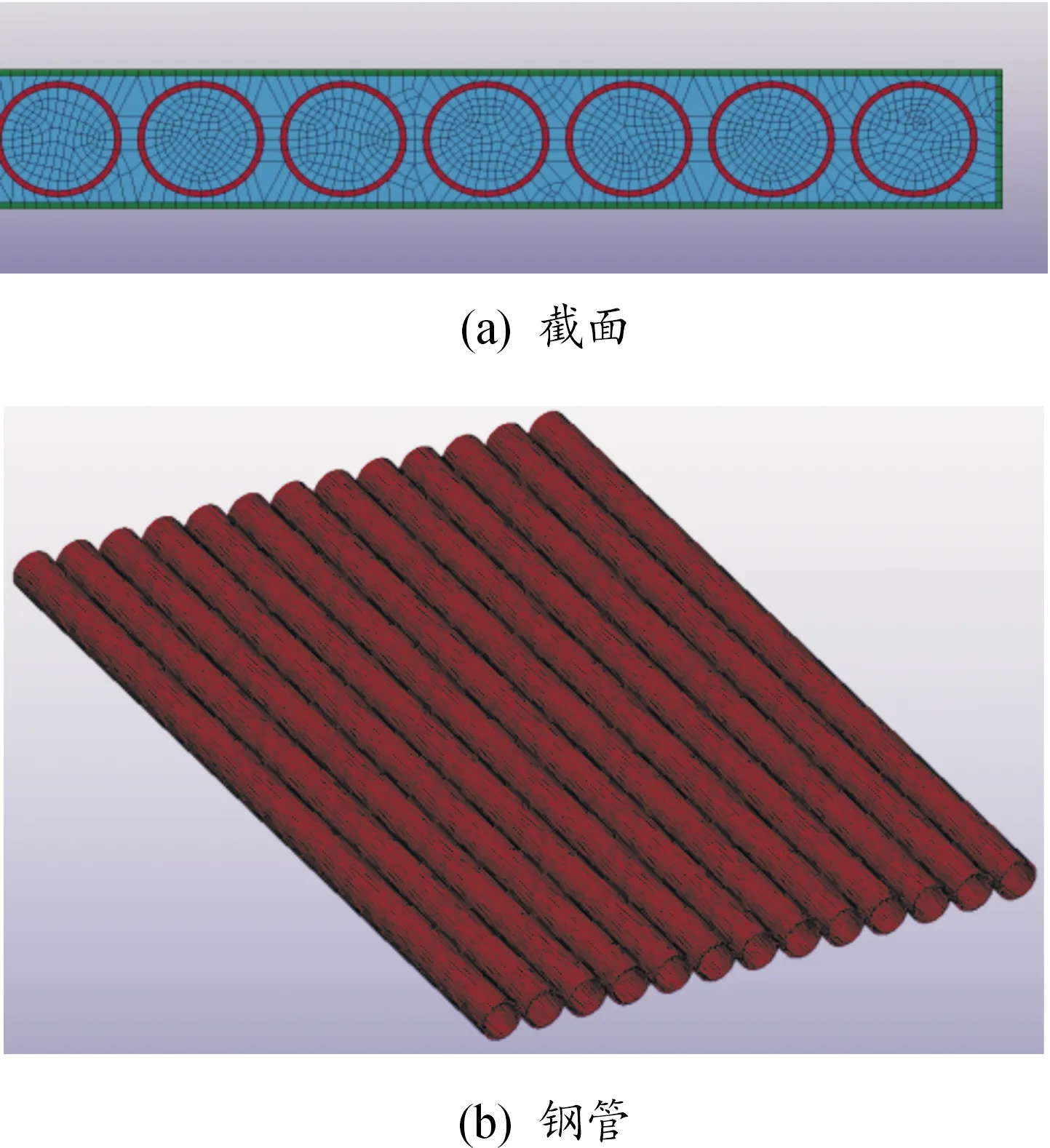
图4 钢包钢管混凝土板模型图

混凝土采用RHT本构模型，该模型可以较好的描述混凝土材料材弹性阶段及进入塑性阶段后材料累计塑性损伤等力学行为，具体的材料参数设置如表1所示：

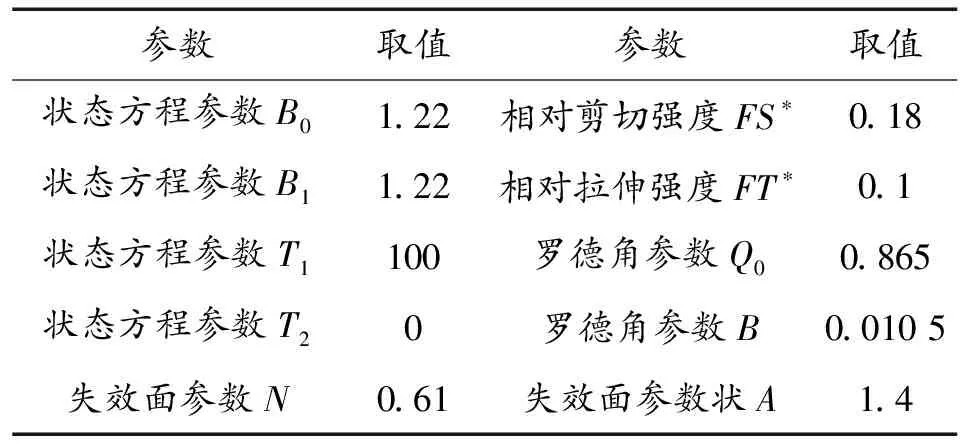
表1 混凝土RHT本构模型主要参数Table 1 Parameters of concrete*RHT

钢材采用弹塑性本构模型，该模型可以较好的描述金属弹塑性阶段的力学行为，满足本文研究问题的需要，且具有较好的运算效率，具体参数如表2所示。

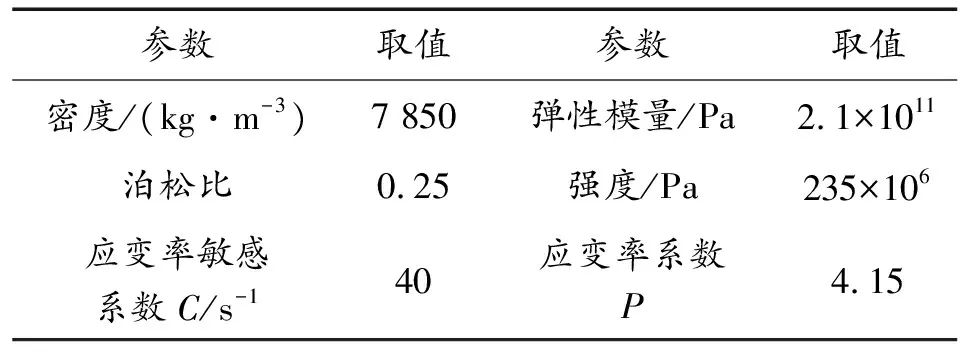
表2 钢的主要参数Table 2 Parameters of steel

3.2 模态分析

为验证1.3节中计算的钢包钢管混凝土简支板的振型及自振频率，通过*CONTROL_IMPLICIT_EIGENVALUE隐式计算方法对2.1中的模型进行模态分析。共设置输出50阶振型。表3给出了不同钢板、钢管厚度的钢包钢管混凝土板的模态频率。

表3 钢包钢管混凝土简支板的模态频率Table 3 Modal analysis of concrete-filled steel and steel tube plate

可以发现，数值模拟及理论计算得到的钢包钢管简支板的基础振型及频率误差较小，证明本文计算方法的可行性。

3.3 爆炸荷载下钢包钢管混凝土的动力响应计算

将爆炸荷载简化为平面均布荷载，作用形式为三角形降压荷载，使用关键字*Load_segment定义。荷载设置为1.5 MPa，正压作用时间为30 ms。钢包钢管混凝土板在塑性阶段的跨中位移最大为10.51 mm，最大塑性应变值为7.2%，板全部进入塑性。图5为钢管最终的Mises应力云图。由图5可以看出板中心及对角线处的Mises应力较大。

4 钢包钢管混凝土动力特性影响因素分析

4.1 弹性阶段自振频率影响因素

按照上述方法对该型号钢包钢管混凝土防护门进行刚度等效后，计算得到该结构的自振频率为1 079.5Hz。将频率、荷载及结构尺寸参数代入式(17)，取前5阶进行计算得到板中心位移的时程曲线如图6所示。

图5 Mises应力云图

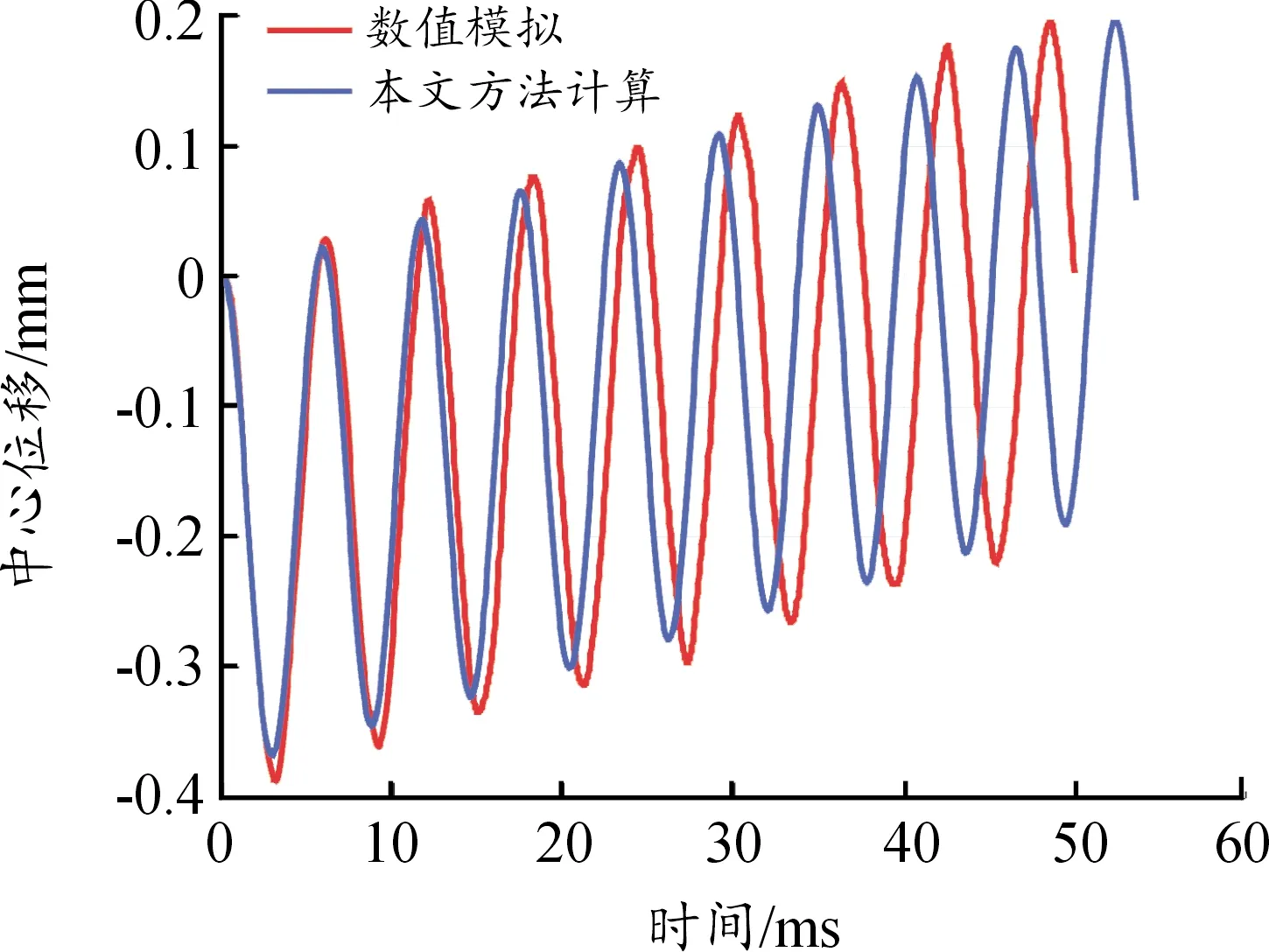
图6 板中心点位移时程曲线

数值模拟与理论计算的中心点时程曲线如图6所示，峰值位移出现时2个方向的振型曲线如图7所示。

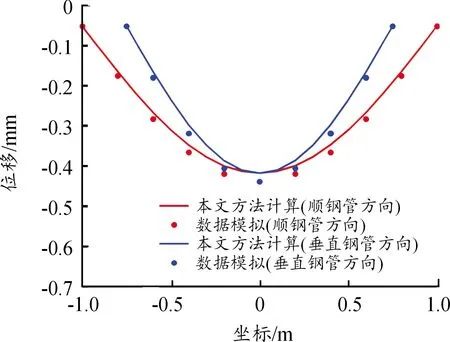
图7 最大位移时振型曲线

图6验证了按照本文方法计算钢包钢管混凝土板自振频率、动力响应结果的准确性。图7验证了钢包钢管混凝土计算中，振型函数选取正弦曲线的合理性。

按照1.4节中的尺寸结构，钢板板厚选取5 mm，并按照不同的钢管管壁厚度计算板的频率，与数值模拟结果进行作图，如图8。

按照1.4节中的尺寸结构，钢管壁厚选取5 mm，并按照不同的钢板板壁厚度计算板的频率，与数值模拟结果进行对比，如图9所示。

图8 频率随钢管壁厚的变化曲线

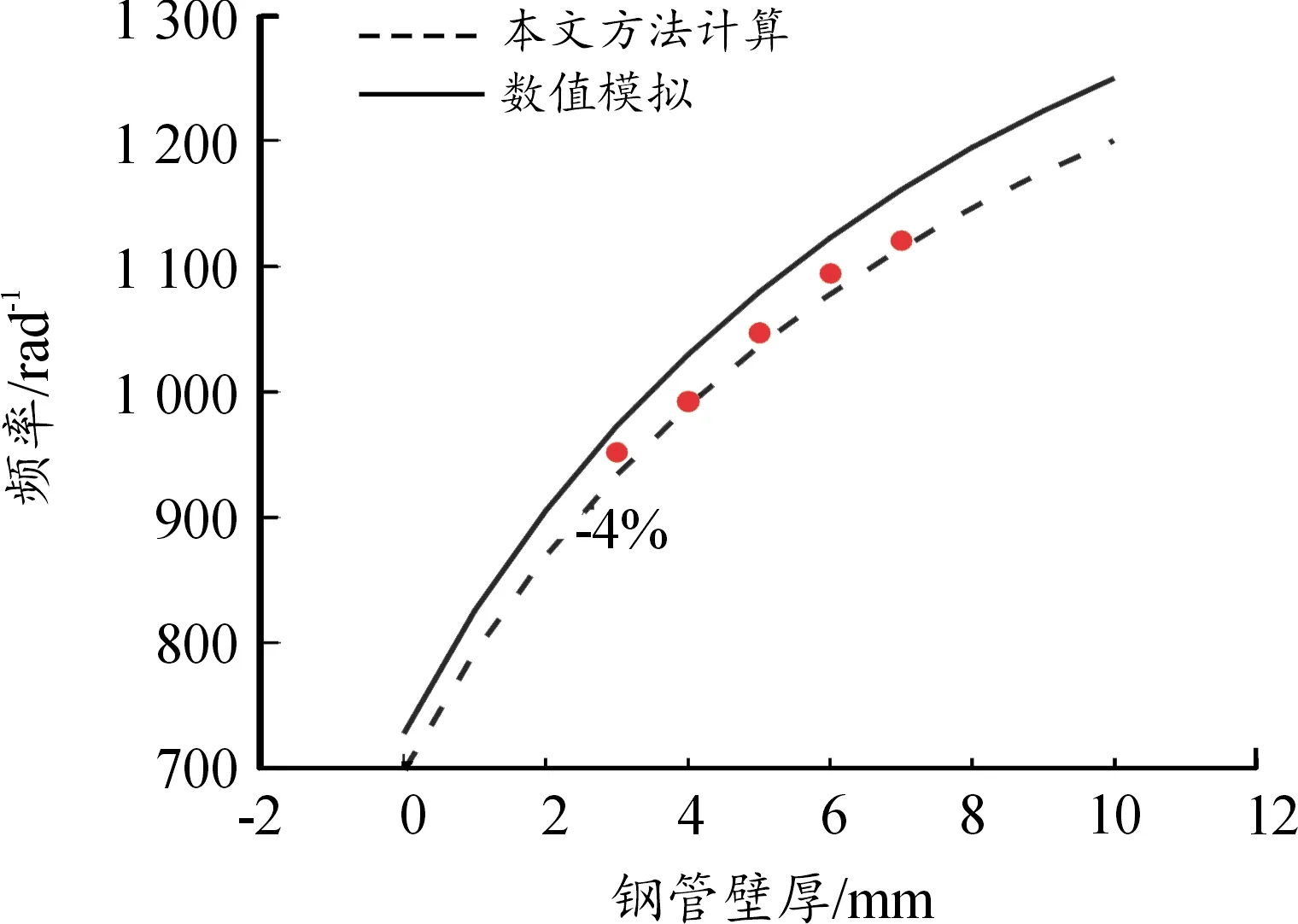
图9 频率随钢板板厚的变化曲线

通过图8、图9可以发现，本文采用的简化等效计算方法得到的钢包钢管混凝土板频率与数值模拟结果规律一致，且误差小于4%。

同时可以发现，板的自振频率随管壁增加反而减小。这是由于钢管管壁的增加虽然可以增加顺钢管方向的抗弯刚度，但壁厚增加带来的密度增加效果更明显，且钢管壁厚的变化对。图9显示，板的自振频率随着钢板板厚的增加而增加，这是由于相较于钢管壁厚，钢板厚度的增加带来的整体密度增加较小，且随着钢板厚度的增加，板2个主方向的抗弯刚度均变大。对比两者的影响程度，可以发现，钢管壁厚度从0增加到10 mm，频率下降了6.5%，钢板板厚从0增加到10 mm，频率上升了41.8%。

4.2 塑性阶段动力特征的影响因素分析

研究了钢管厚度和钢板厚度对钢包钢管混凝土板塑性阶段动力响应的影响，进行除钢管壁厚度和钢板厚度取值不同，其余参数相同的5组数值模拟，分别为5 mm-5 mm、5 mm-7 mm、5 mm-10 mm、7 mm-5 mm、10 mm-5 mm(钢管壁厚度-钢板厚度)。

图10展示了随着钢管壁厚度的增加，板的中心位移也逐渐增加，但变化幅度较小。图11可以看出随着钢板厚度的增加，板的中心位移随之增加，变化效果较明显。

图10 钢管壁厚度与板中心点位移曲线

图11 钢板厚度与板中心点位移曲线

5 结论

1) 将钢包钢管混凝土防护门简化为一种正交各向异性简支板，计算了钢包钢管混凝土防护门2个主方向的抗弯刚度、泊松比、自振频率及弹性阶段动力响应。

2) 通过数值模拟计算，验证了本文计算方法的准确性及振型函数选取正弦函数的合理性，理论计算得到的频率与数值模拟结果误差小于4%。

3) 钢包钢管混凝土板的自振频率随钢板厚度增加而增加，变化效果明显；随钢管壁厚增加而减小，减小幅度较小。

4) 钢包钢管混凝土防护门的抗力随着钢板厚度的增加而增加；随着钢管壁厚的增加而增加，变化幅度不明显。