基于模糊逻辑的导弹PID/滑模复合控制器设计

陈 喆，吕 瑞，杜 肖，葛云鹏

(中国运载火箭技术研究院，北京 100076)

1 引言

作为弹上核心控制单元，导弹武器的精确打击离不开优良的自动驾驶仪设计，经过众多科研工作者长期的设计改良与研究发展，如今导弹自动驾驶仪已经衍生出了多种设计结构，如两回路结构、三回路结构、PI校正结构、伪攻角控制结构等，控制器设计方法也从古典频域设计开始向滑模控制、鲁棒控制、神经网络等现代控制方法转变，各式各样百花齐放。随着计算机算力日益提升，甚至在线弹性迭代、机器学习、强化学习等智能方法也在自动驾驶仪设计中逐步得到应用。

由于单一控制器设计方法在有些环境下会存在弊端或出现不优甚至不适用的情况，如文献[7]针对驾驶仪全包线控制提出了基于动压插值的综合增益调度方法，保证了全包线飞行的鲁棒镇定。滑模变结构控制由于响应速度快、鲁棒性强等优点，已经广泛被用来解决各种参数不确定或非线性控制系统问题并取得一定控制效果，但在滑模面附近容易产生抖振。文献[8]采用滑模控制时则通过切换增益变结构避免了控制量的频繁抖振。为了提高自动驾驶仪控制能力，各研究人员也在单一控制方法的基础上加入了多控制复合，如文献[9-10]针对直/气控制导弹提出动态面与自适应复合控制方案，解决了多执行机构下的协调配合问题。

控制分配作为复合控制的关键决定着控制器性能的优劣，文献[11-12]通过构造目标函数或控制分配权系数优化模型提出了各自的自适应动态加权分配策略，实现了复合控制的最优分配。考虑模糊逻辑具有对参数摄动不确定性进行逼近的能力，本文从兼顾算法实现及工程应用的角度出发，为提高自动驾驶仪综合控制性能，提出了一种基于模糊逻辑分配策略的线性PID+滑模复合控制器设计方法，同时也避开了基于现代控制方法的复合控制器设计在建模及实现时都略显复杂的方式，达到了设计简单、优势互补的目的。

2 导弹自动驾驶仪模型

在导弹运动三维非线性模型的基础上进行通道解耦并线性化，可得到导弹运动的线性模型。以俯仰通道为例，典型的两回路过载自动驾驶仪结构一般由阻尼内回路和过载外回路两部分组成，输出为法向加速度(或法向过载)，其控制回路结构如图1所示。

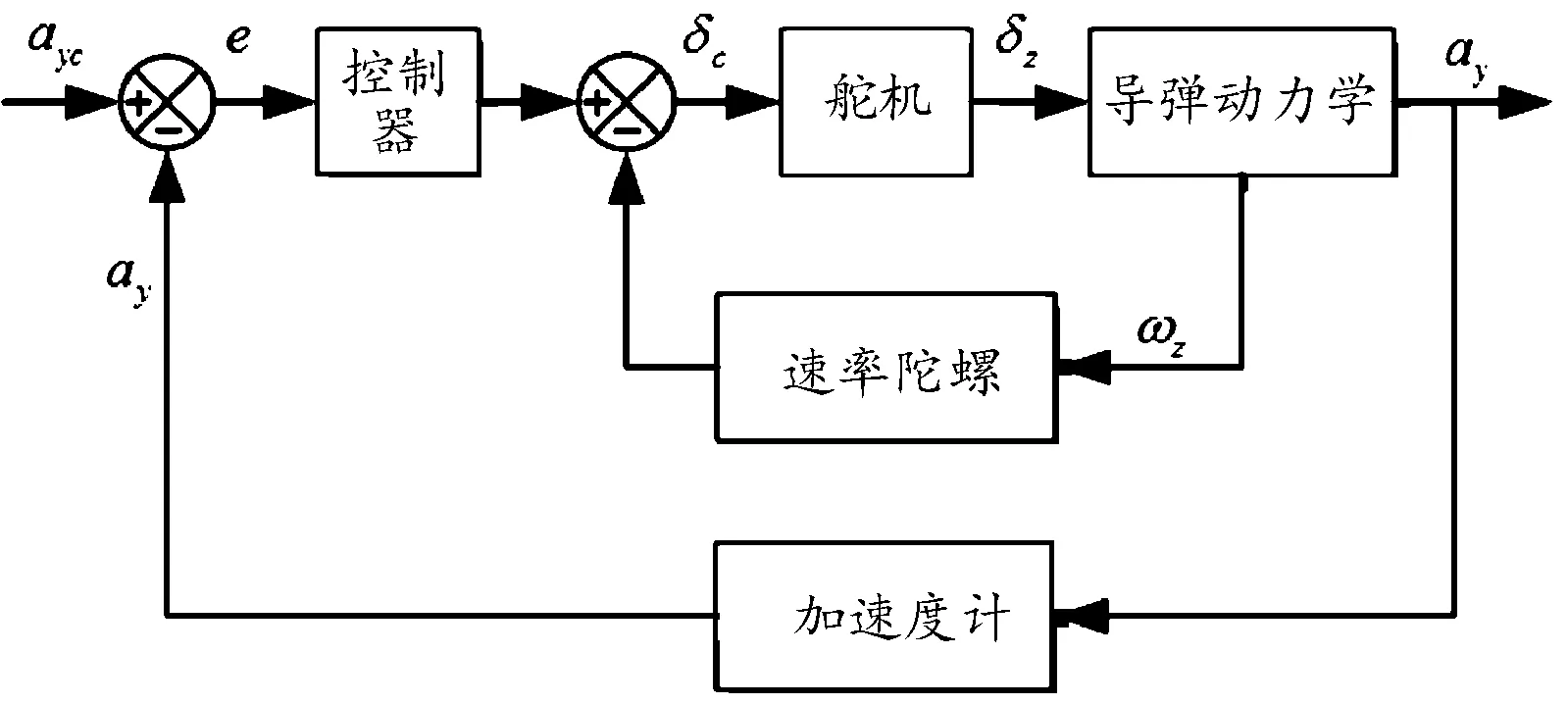
图1 过载自动驾驶仪控制回路结构示意图

STT控制方式下过载自动驾驶仪俯仰通道线性化动力学方程为

(1)

式中:、、、、分别为与导弹飞行相关的动力学参数；、、、分别为导弹的俯仰角速率、飞行攻角、弹道倾角以及俯仰舵偏角；、则为导弹速度与法向加速度。

将方程式(1)左右两边分别进行Laplace变换，可以得到关于弹体动态特性的传递函数为

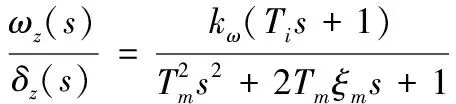
(2)

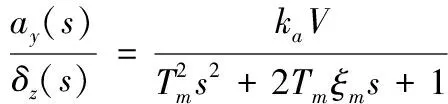
(3)

其中:、为弹体开环时间常数与阻尼系数；为攻角滞后时间常数；、分别为相应传递函数中的比例系数，具体表达式如下

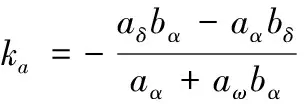
3 单一控制方式设计

3.1 线性PID控制设计

传统的两回路过载自动驾驶仪是0型系统，虽然响应速度快但存在一定的稳态误差，若在控制回路中加入PI校正，则能更好的跟踪输入变化，减小系统本身存在的静差，类似于三回路自动驾驶仪的积分增稳回路。线性PID控制自动驾驶仪回路如图2所示。

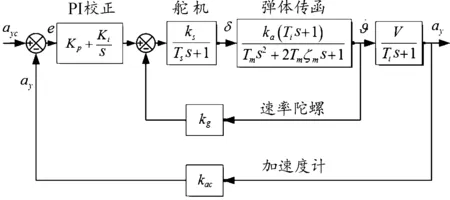
图2 线性PID控制自动驾驶仪回路结构示意图

(4)

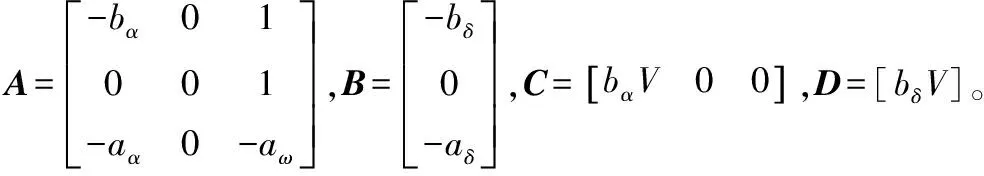
对于线性PID控制自动驾驶仪，极点配置方法是设计控制参数的一种有效手段，若采用如图3所示的状态反馈方式。

则状态反馈下受控系统的输入为

=-x+′

(5)

式中：为状态反馈增益矩阵，′为期望状态值。

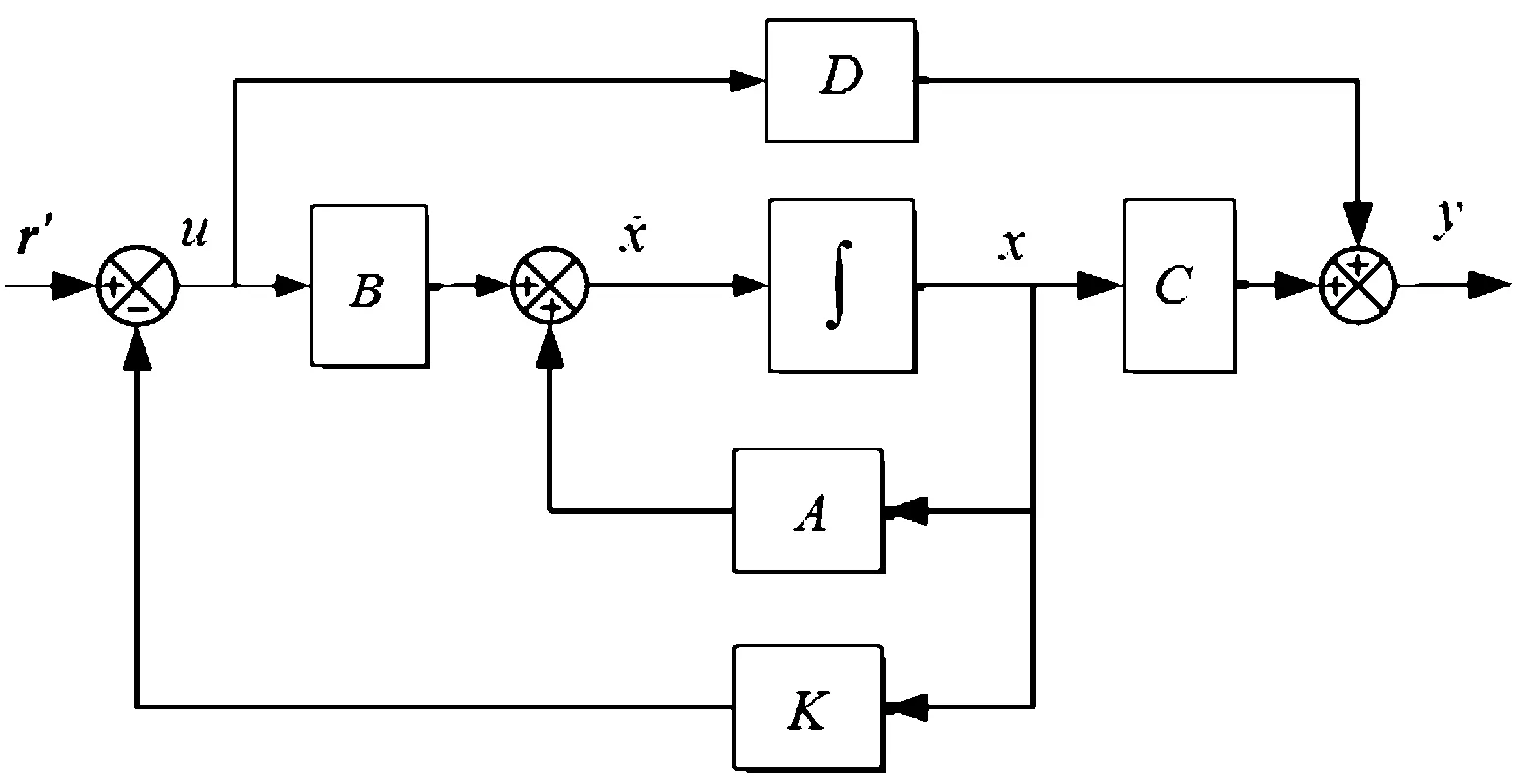
图3 状态反馈结构示意图

若采用如图4所示的输出反馈形式。

图4 输出反馈结构示意图

则输出反馈下受控系统的输入为

=-y+

(6)

其中：为输出反馈增益矩阵，为期望输出值。设系统的输出反馈可用状态反馈实现，由式(4)与式(5)可知=-((-u))+′，展开后可得

=-(-)+(-)′

(7)

记=(-)′，则输出反馈的增益矩阵为

=(-)

(8)

进行参数设计时可将自动驾驶仪各回路反馈值叠加到图2舵偏角位置，并用状态变量、、来描述

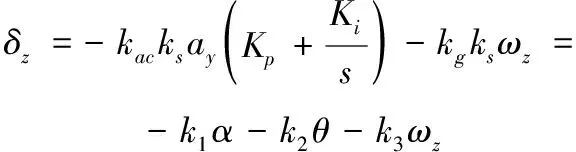
(9)

其中、、为状态反馈增益矩阵的子元素，具体如下:

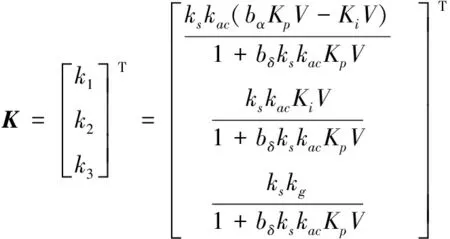
(10)

根据矩阵及式(8)则可求得输出反馈增益矩阵为

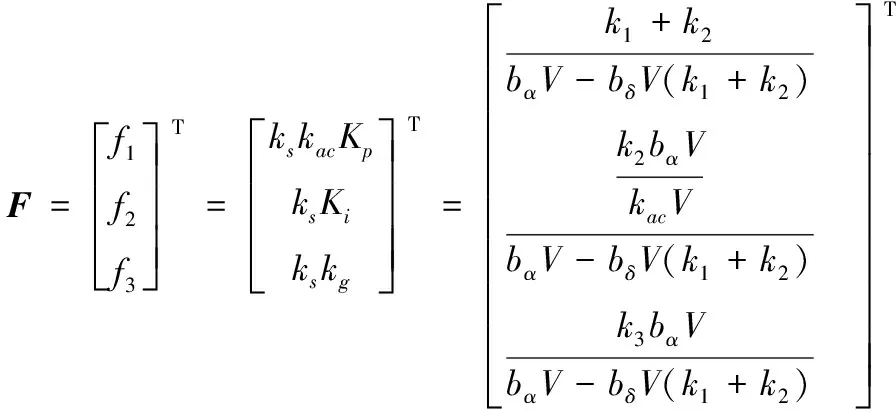
(11)

因此带PI校正的两回路过载自动驾驶仪设计参数为

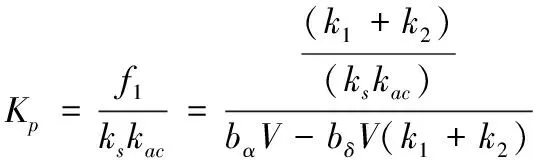
(12)

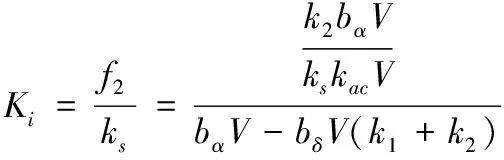
(13)

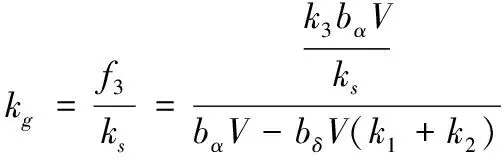
(14)

3.2 滑模变结构控制设计

在带PI校正过载自动驾驶仪控制结构上引入滑模控制，则控制鲁棒性可得到增强，弹体相关的传递函数与PID控制自动驾驶仪相同，如图5所示。

图5 滑模控制自动驾驶仪回路结构示意图

根据式(3)的被控对象传递函数经Laplace反变换有

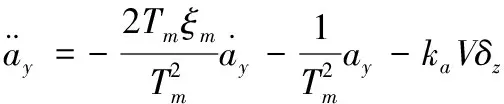
(15)

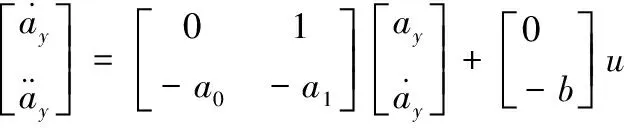
(16)

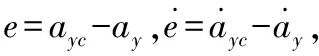
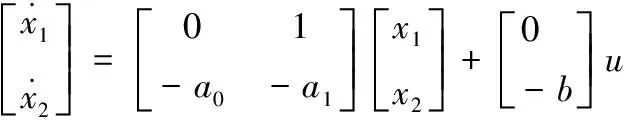
(17)

滑模面采用如下函数：

(18)

切换函数采用误差比例切换

=·||·sgn()

(19)

式中: sgn为符号函数；为比例切换系数，根据误差大小调节能够实现过载快速控制，并有效地抑制滑模系统抖振的幅值。

4 模糊逻辑复合控制器设计

基于上述线性PID与滑模控制设计，在自动驾驶仪上融合这2种设计思想，通过过渡切换实现取长补短，得到鲁棒性更强、适用范围更广的PID/滑模复合控制自动驾驶仪，如图6所示。

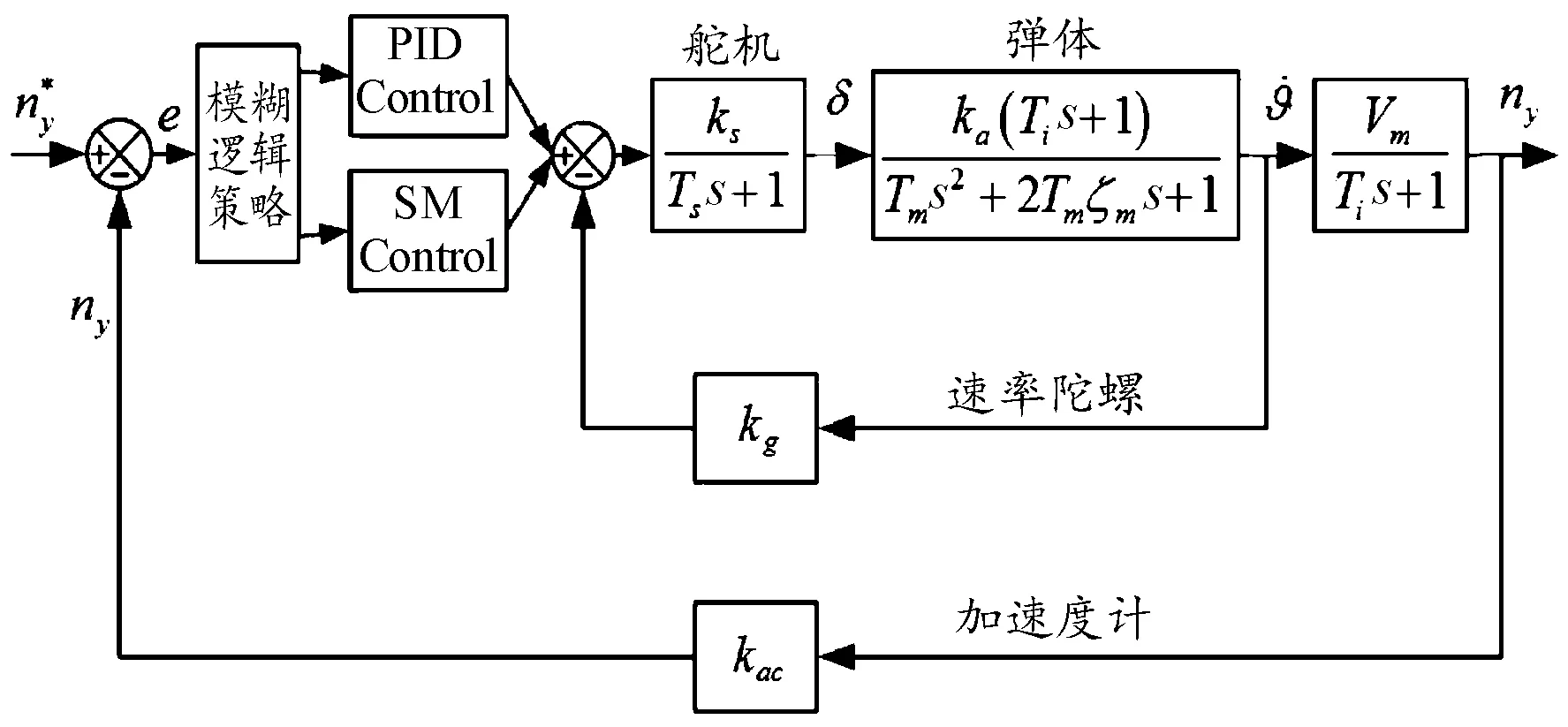
图6 PID/滑模复合控制自动驾驶仪回路结构示意图

使用多控制器复合时类似于多执行机构复合，会涉及到控制的协调与分配问题，由于模糊控制具有对参数摄动不确定性进行逼近的能力，因此在自动驾驶仪复合控制分配策略上采用模糊逻辑对2种控制的切换使用进行权值分配设计。由于存在参数摄动时控制需求体现在过载及攻角上的变化较为明显，以自动驾驶仪的过载误差及攻角大小作为模糊逻辑的输入参考量，以滑模控制的权值(,)作为参考输出。则PID控制与滑模控制各自的控制输入量可表示为

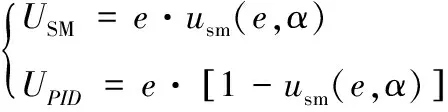
(20)

式中：为滑模控制输入量；为PID控制输入量；为自动驾驶仪全局控制误差；(,)为滑模控制分配的权值，范围0～1，取0时表征完全采用PID控制，取1时表征完全采用滑模控制。外部飞行环境变化时根据采用的模糊规则对自动驾驶仪复合控制进行增益调节。

对于模糊逻辑隶属度函数的设置，模糊区间采用等距划分，为了使复合控制的切换平缓稳定，隶属度函数取为高斯函数，在攻角输入的论域上定义5个子集：、、、、；在过载偏差输入的论域上定义4个子集：、、、；滑模控制分配输出的论域上定义5个子集：、、、、，具体如图7所示。其中，输入参考量过载误差及飞行攻角的隶属度函数曲线宽度相对较大，适合于较大范围的平稳过渡；输出量滑模控制的权值函数曲线宽度相对较小，便于不同环境下的控制侧重使用。

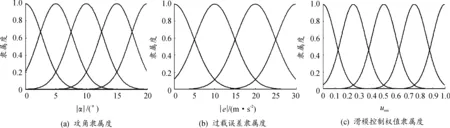
图7 模糊逻辑输入输出参考量隶属度函数曲线

为了使控制权值的变化比较平滑，避免控制律切换对系统稳定性造成影响，需要对模糊逻辑规则进行优化，经过优化后得到模糊控制规则如表1所示。

表1 控制分配模糊规则表Table 1 Fuzzy rule of control allocation

5 仿真验证与分析

结合以上推导与复合控制设计方法，以某导弹机动飞行段为例进行仿真研究及分析。导弹飞行速度介于2.0～3.2，飞行攻角绝对值在0°～18°之间，自动驾驶仪相关控制参数设计以表2中某末制导特征点动力系数为准。

表2 导弹某特征点动力系数Table 2 Dynamic coefficients of feature point

舵机模型参数=-0.013、=0.01，控制参数=1.4，=6.5，=34.1，=9.9，=1.5，表2特征点处导弹期望的法向加速度大小(加速度指令)为13.18 m/s，飞行环境气动参数摄动在-20%～+20%的范围。

根据给出的仿真条件，按上文提到的3种自动驾驶仪设计方法：单独PID控制；单独滑模控制；PID+滑模复合控制，得到控制器在参数摄动下的响应结果如图8—图10所示。

图8 PID控制自动驾驶仪过载响应曲线

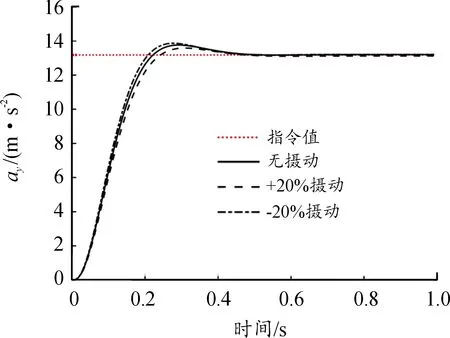
图9 滑模控制自动驾驶仪过载响应曲线

图10 复合控制自动驾驶仪过载响应曲线

3种控制模式在+20%参数摄动下的上升时间与超调量对比如表3所示。

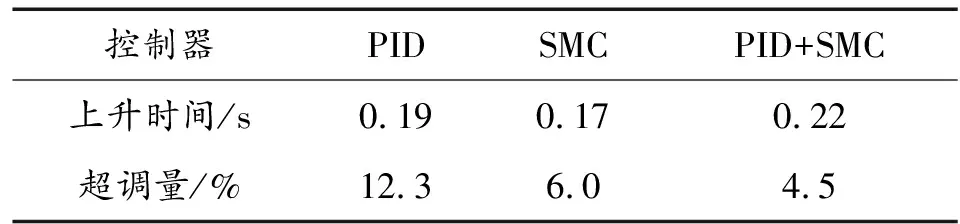
表3 上升时间与超调量对比Table 3 Comparison of rise time and overshoot

仿真结果中图8—图10的自动驾驶仪过载响应曲线较明显地体现了3种自动驾驶仪在同一环境下的响应能力及参数摄动对控制器效果的影响。滑模控制相对不敏感，复合控制则居于PID控制与滑模控制之间。

复合控制权值分配及舵偏响应如图11、图12所示。

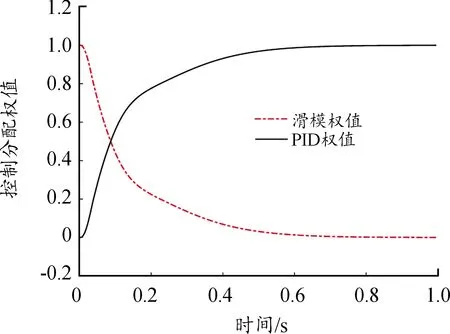
图11 复合控制权值分配曲线

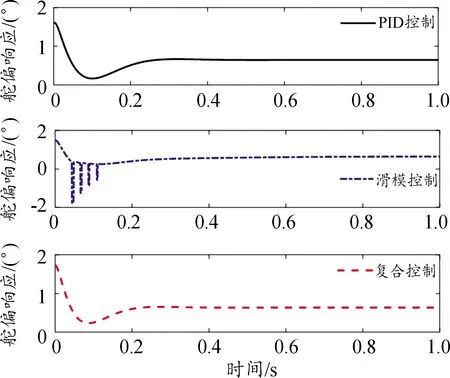
图12 复合控制舵偏响应比较曲线

从图11、图12仿真结果来看，采用复合控制策略时，控制偏差相对较大时滑模控制占主导，快速缩小控制误差。随着误差逐渐收敛，图11中大概在0.1 s时刻控制器作用效果开始转变，控制器分配权值开始向PID控制倾斜，逐步达到稳态精确控制。在未知飞行环境出现参数摄动的情况下，相比单一控制方法，该PID/滑模复合控制自动驾驶仪集各家所长既不失控制精确性，也具备较强鲁棒性，控制效果有较好提升。

6 结论

为提高过载自动驾驶仪在参数摄动情况下的控制鲁棒性，本文提出的PID+滑模复合控制器设计方法通过模糊逻辑策略根据过载误差及飞行攻角调整复合控制的分配权值，实现了控制器随外部参数摄动变化自适应调整控制分配的目的，且兼具快速响应与强鲁棒性的特点。与传统单一控制方法进行比较，仿真结果验证了该复合控制器在满足控制稳定需求的同时，对于飞行环境中参数摄动具有较强的适应能力，提升了导弹的综合控制性能。