基于机器视觉的高精度微纳光纤直径实时测量
李华 麻艳娜 谷付星





摘要:针对传统微纳光纤直径测量方法操作复杂、重复性差且易于损伤光纤等问题,开发了一套基于机器视觉的微纳光纤直径测量系统。首先,对系统采集的图像进行预处理和二值化分割,其次,通过 Canny边缘算子实现微纳光纤边缘初定位,最后,基于改进 Zernike 矩的亚像素检测方法精确定位了亚像素级边缘。此外还提出了结合 Hough 变换与最小二乘法的算法拟合亚像素级边缘点的方案,将系统微纳光纤直径测量精度提升至纳米级。实验测量结果表明,该系统可实现3.51%以内误差的自动化测量,运行时间为2.671 s,更适用于微纳光纤尺寸的高精度实时测量。
关键词:微纳光纤;直径测量;机器视觉;图像分割;边缘检测
中图分类号: TP 391.4; O 434.3 文献标志码: A
High-precision and real-time measurement of micro-nano fiber diameter based on machine vision
LI Hua,MA Yanna,GU Fuxing
(School of Optical-Electrical and Computer Engineering, University of Shanghai forScience and Technology, Shanghai 200093, China)
Abstract: To solve the problems of complex operations, poor repeatability, and contact damage in traditional micro-nano fiber diameter measurement methods, a new measurement system based on machine vision was developed. Firstly, the image was preprocessed and binary segmented in the system, and then the edge of micro-nano fiber was initially located by the Canny edge operator. After that, a sub-pixel detection method based on improved Zernike moment was used to accurately locate the sub-pixel edge. Besides, our system also proposed an algorithm combining Hough transform and the least square method to fit sub-pixel edge points, which improved the measurement accuracy of micro-nano fiber diameters to the nanometer level. The measurement results of micro-nano fiber diameter show that the system can achieve high automation with a measurement error of less than 3.51%, and the running time is 2.671 s. It can be applied to the high- precision and real-time measurement ofmicro-nano fiber morphology.
Keywords: micro-nano fiber; diameter measurement;machine vision; image segmentation; edge detection
引言
目前,聚二甲基硅氧烷复合微纳光纤、石墨烯复合微纳光纤等材料已经成为微纳光纤领域的热点研究课题。其中,微纳光纤的形貌对相关微纳光纤功能器件[1]的性能具有决定性的影响。因此,微纳光纤传感器件[2]的研究对光纤直径的控制与测量提出了很高要求。
近年来,微纳光纤直径测量技术快速发展。利用扫描电子显微镜可实现分辨率达亚纳米量级的微纳光纤成像,然而顯微镜中的高能电子会对被测试样品造成不可逆的伤害。Warken等通过对光纤衍射图样的采集分析[3-4],实现了50 nm 测量精度的光纤直径检测。Sumetsky等则通过检验纳米光纤中回音壁模式的共振峰测量其直径[5],分辨率可低至0.1 nm 量级,但无法得到直径的准确值。此外,Keloth等还提出了一种利用缺陷模光栅构成的光子晶体微腔与微纳光纤接触,通过其共振峰测量光纤直径的方案[6],测量分辨率可达10 nm ,但是该方案需要五维调节对准微腔与微纳光纤的位置,实验操作难度大且重复性差。传统微纳光纤直径测量法在实际应用中逐渐暴露出重复性差、操作难度大以及容易损伤光纤等问题。因此,本文提出了一种利用机器视觉实时测量微纳光纤直径的方案,涉及到的视觉算法包括图像增强、边缘检测等。
图像增强是一种基于图像分割和图像理解的预处理算法。在图像采集和传输过程中,成像效果易受到光照噪声和传输噪声的影响,需要先对图像进行滤波去噪而后进行分割。
日本的大津展之提出最大类间方差法(Otsu)分割图像[7]。该方法以图像的灰度直方图为基础,通过设置合适阈值来计算目标区域和背景区域的类间方差。当该方差函数到达最大值时,此时的阈值即为所需阈值。增强图像后,需要通过边缘检测提取被测物体轮廓。边缘检测常用的算子有 Laplacian 算子、 Prewitt 算子和 Canny 算子[8]等。以上算子都是像素级别的,而在实际生产中往往需要达到亚像素级别[9]的检测精度。目前,获取亚像素边缘点的方法主要有三种:空间矩法、插值法和拟合法。Lyvers等首先使用几何矩得到图像亚像素边缘[10],该方法利用六个几何矩计算阶跃边缘参数,因其图像矩的多项式并不正交,所以会产生大量的无效计算[11]。随后,Ghosal 等提出了利用 Zernike 正交矩获取精确亚像素边缘点的方法[12],但是其在计算中需要手动设置亚像素点判定条件,不仅精度较低,而且耗时较长,不利于批量处理图像。
针对现有应用机器视觉进行微纳光纤直径测量方向的空缺,本文通过图像预处理、图像二值化分割、边缘检测以及直线拟合等方法,搭建了一套基于机器视觉的高精度微纳光纤直径实时测量系统,可精确提取拟合光纤边缘并分析计算光纤直径。该系统稳定性强,可批量处理图像,具有良好重复性;系统仅增加了相机和计算机即可实现测量,操作简单;而且该系统属于非接触式测量,可避免移动光纤造成的污染和损伤。
1 基于机器视觉的微纳光纤直径检测方法
微纳光纤直径测量步骤主要有图像预处理、图像分割、 Canny边缘检测边缘点粗定位、亚像素边缘检测边缘点精确定位和微纳光纤轮廓拟合五个部分。最后利用标定获得的相机标定系数将像素长度转换为实际长度,计算微纳光纤的准确直径。
图像预处理用于将原始图像转变为灰度图像,并采用拉普拉斯算子变换[13]的方法实现图像增强,增加明暗区域对比度,并通过中值滤波去除图像随机噪声。图像分割则将预处理后的图片分割成拥有共同特征的不同的部分。本文采用 Otsu 法选取灰度阈值,根据像素点的灰度值将图像转变为二值图像。而后通过 Canny边缘检测算法提取图像中灰度值急剧变化区域的点,实现边缘点初定位。
该机器视觉检测方案而后基于改进的 Zernike 矩实现亚像素边缘的精确定位。该检测算法通过三个不同阶次 Zernike 矩计算阶跃灰度模型参数,并通过四个参数计算确定目标边缘。
图像f(x,y)的二维 Zernike 矩表述为
式中: f(x,y)为图像点(x,y)处的灰度值; V m(;)
为Vnm(;)的复共轭;Vnm(;)为极坐标系单位圆内 Zernike 矩的 n 阶次多项式。
离散条件下,图像f(x,y)的二维 Zernike 矩在单位圆内定义为
Zernike 矩Znm旋转φ角度后Znm关系函数定义为
Z′nm = Znme−imφ (3)
由式(3)可知,图像旋转后模相同,仅仅相位
改变,由此可以定义为 Zernike 矩的旋转不变性。
如图1所示,在单位圆内直线 L 两侧的灰度值分别为 h 和h+k,其中k 为灰度阶跃差值,原点到边缘的理想长度为 l ,φ为线段 l与 x轴的夹角。图1(b)为图1(a)旋转φ角度后的图像。
Re[Zn1]和Im[Zn1]分别是 Zn1的实部和虚部。根据旋转后不同阶 Zernike 矩可求得φ、l、k、 h 四个参数分别为
由此灰度阶跃模型可演算出亚像素边缘检测的公式为
缘点的判决条件为k ⩾Kt ∩ l ⩽lt,其中Kt和lt为阈值。 Kt取值范围比lt大得多,其取值一直是实验中的重点,对于实验结果有较大影响。本文通过 Otsu 的自适应灰度阶跃阈值法确定阈值 Kt。
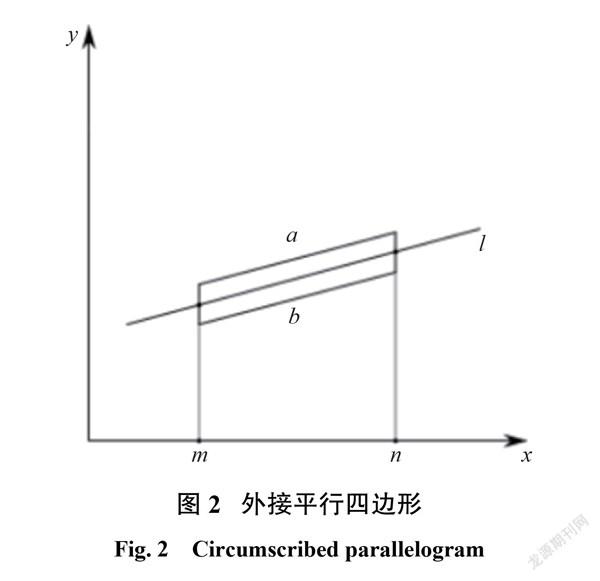
本文最后结合 Hough 变换(Hough transform, HT)[14]和最小二乘法( least square method,LSM)[15-16],實现微纳光纤边缘的实际检测。首先使用 Hough 变换量化参数空间,接着统计累加器的值,若值为一定邻域内极大值,则可得到一条直线的大致位置,直至找出所有直线。然后对直线作外接平行四边形,如图2所示,四边形的长宽可以根据数据点分布选取合适值,最后将落入平行四边形内的数据点拟合成一条直线。该方法具有强鲁棒性,当光纤内部光场分布不规律时,仍然能准确拟合光纤外边缘,使得实验结果具有更高精度。
2 实验结果和结果分析
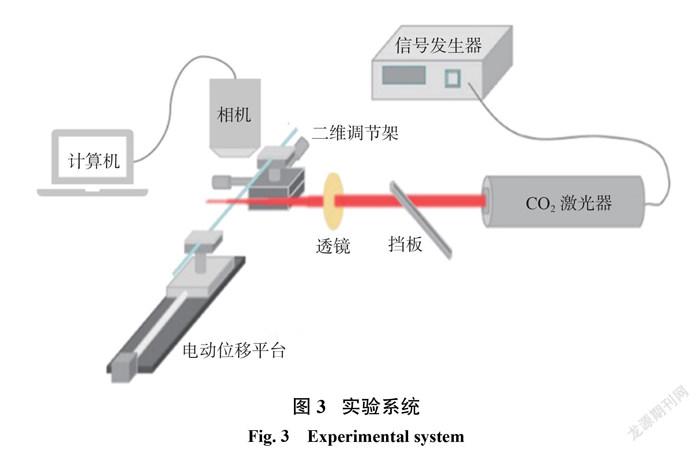
该微纳光纤直径测量系统包括光纤制备[17]和图像采集两个部分,如图3所示。其中光纤制备系统包括信号发生器、 CO2激光器、电动位移平台和二维调节架。 CO2激光器用于产生红外激光和加热熔融光纤。信号发生器的作用是通过改变脉冲信号占空比调节 CO2激光器输出功率。电动位移平台和二维调节架分别用于拉制光纤和调节光纤摆放位置。图像采集系统包括工业相机、相机支架、镜头、照明系统和计算机。相机和镜头分别采用图谱光电130万像素的 LCMOS01300KPA 工业相机和日本尼康公司 CF Plan 100×的低畸变镜头,相机标定系数为0.06398μm/pixel。照明系统选择 LED 光源前景光照明。实验系统将相机与计算机连接,通过Toupview软件获取图像,并使用 MATLAB 软件进行图像处理。实验过程中实时采集图像,并通过机器视觉处理系统批量处理。
2.1 图像处理及边缘定位
采集图像后对图像进行预处理。由图4(b)可以看出,经过拉普拉斯算子运算和中值滤波后,图像边缘对比度更高,细节更加突出。接着使用 Otsu 阈值分割法,对图像进行二值化分割,如图4(c)所示,尽管照射光源产生的光在光纤-空气界面发生反射和折射,使得光纤内部光场分布并不均匀,但是该算法仍然能够获得清晰完整的光纤外轮廓信息。
微纳光纤图像可通过 Canny算子检测出清晰、单像素连续的边缘,如图5(a)所示,初定位结果准确性较高。将图像中從上至下的四条边缘分别标记为边缘1、边缘2、边缘3和边缘4。边缘1和边缘4为与背景相邻的光纤外部轮廓,是有效边缘信息。因为其保存了光纤直径信息,将作为后续实验的核心研究对象。微纳光纤内部光场分布不均,边缘2和边缘3为 Canny 算子可以检测到的内部假边缘,后续将其忽略。而后通过改进的 Zernike 矩亚像素边缘检测算法,提升微纳光纤直径测量精度,如图5(b)所示,将边缘细化到亚像素级,准确提取出极细的光纤外边缘。两级边缘检测算法,减少了运算复杂度,将运算时间减少到约1.7 s。此外利用 Otsu法求取灰度阈值Kt,也有利于批量处理图片,简化处理流程。
2.2 直线拟合仿真
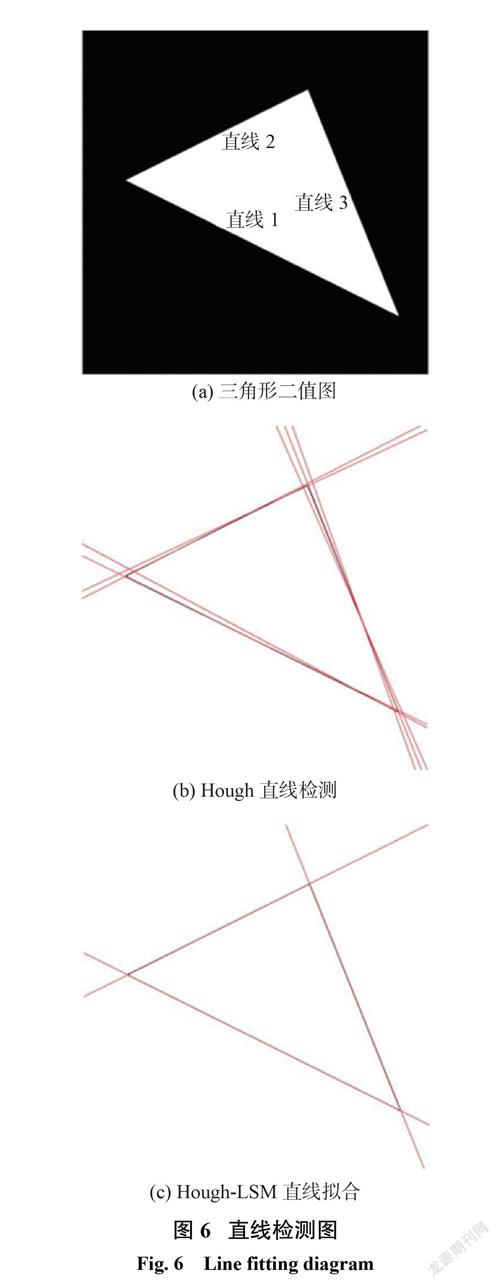
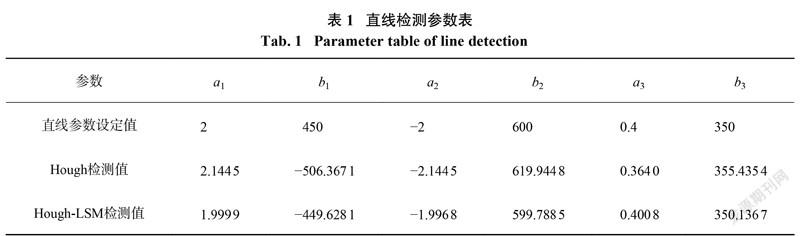
系统仿真验证了 Hough-LSM算法的测量精度。图6(a)为一张600 pixel×600 pixel 像素的三角形图像,图上有直线1(y=2x−450),直线(2y=−2x+600)和直线3(y=0.4x+350)。记直线1斜率和截距分别为 a1和 b1,直线2斜率和截距分别为 a2和 b2,直线3斜率和截距分别为 a3和 b3。直线检测参数列如表1中所示。
黑色直线为三角形图像边缘,红色直线为算法检测出的直线。传统 Hough 算法检测出了若干错误直线,精度较低,如图6(b)所示;而本算法拟合出的直线与原图直线基本重合,如图 6(c)所示。Hough-LSM算法计算斜率的最大误差为0.0032,截距最大误差则为0.3719。因此,本方案提出的 Hough-LSM算法准确率极高,适用于微纳光纤直径的高精度测量。
在仿真测量中,该方案首先对 Canny算子检测出的边缘点进行 Hough 变换,求出两条直线的大致直角坐标方程以及拟合区域,而后进行 Hough-LSM算法拟合检测。如图7(a)所示,算法可实现亚像素边缘点的有效拟合,能准确检测出光纤外侧边缘位置。图7(b)则验证了算法拟合直线与光纤轮廓的重合度。
2.3 测量结果分析
实验采集了多根微纳光纤样品,并将本文算法测得的物理直径与手工测量结果进行对比,比较分析误差。在实际应用中,微纳光纤两侧轮廓的形貌并不能达到理想的平行,仅通过平行线距离计算公式得到的结果并不准确。因此本文选取了其中一条直线段,并取点将线段分为数等份。此时两条直线段距离即等效为数点到另一条直线段距离的均值。具体步骤如下。取其中一条直线上9个点 pi(xi ;yi)(i =1;2;:::;9),分别计算各个点到另一条直线axi+ byi+ c =0的距离 di,即
然后对上述距离取均值,求得微纳光纤的像素直径d,即
而后将光纤像素直径乘以标定系数,即可得到微纳光纤实际物理直径。
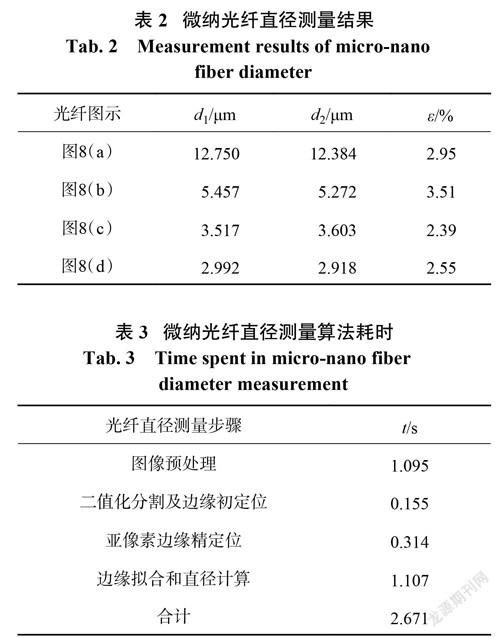
实验对整个过程进行监测,获取图像并计算微纳光纤直径,4种光纤直径变化情况如图8所示。在实验中使用高倍显微镜进行人工测量,测量误差为±0.064μm。记机器视觉计算的直径值为d1,人工测量值为d2,误差为ε,各参数测量结果如表2所示。由测量结果可得,本方案的直径测量误差在3.51%以内。此外,还记录了测量多根微纳光纤直径过程中每个步骤耗时和总耗时的均值,测量结果如表3所示。整个实验过程共耗时2.671 s ,可基本满足微纳光纤的实时测量需求。
3 结论
本文开发了一套基于机器视觉的微纳光纤直
径测量系统。相较于传统的微纳光纤直径测量方法,该系统将机器视觉检测技术引入微纳光纤的直径测量中,运行稳定且速度快,测量结果精度高,有较强鲁棒性。本文利用 Otsu 法改进了亚像素边缘检测算法,可避免频繁的手动取值且具有高测量精度。而后结合 Hough 变换和最小二乘法的优点提出 Hough-LSM算法,可在复杂的光纤内部光场分布情况下实现亚像素边缘点高精度拟合。通过实验测量,系统的直径测量误差在3.51%以内,运行时间为2.671 s ,满足了高精度和实时测量的要求,对微纳光纤制备过程的光纤形貌监测有很大借鉴意义。
参考文献:
[1] LINGHU S Y, GU Z Q, LU J S, et al. Plasmon-drivennanowire actuators for on-chip manipulation[J]. Nature Communications, 2021, 12(1):385.
[2] LIAO F, YU J X, GU Z Q, et al. Enhancing monolayerphotoluminescence on optical micro/nanofibers for low-threshold lasing[J]. Science Advances, 2019, 5(11): eaax7398.
[3] WARKEN F, GIESSEN H. Fast profile measurementof micrometer-sized tapered fibers with better than 50-nm accuracy[J]. Optics Letters, 2004, 29(15):1727–1729.
[4] LITTLE D J, KANE D M. Subdiffraction-limited radi-us measurements of microcylinders using conventional bright-field optical microscopy[J]. Optics Letters, 2014,39(17):5196–5199.
[5] SUMETSKY M, DULASHKO Y. Radius variation ofoptical fibers with angstrom accuracy[J]. Optics Let- ters, 2010, 35(23):4006–4008.
[6] KELOTH J, SADGROVE M, YALLA R, et al. Dia-meter measurement of optical nanofibers using a com- posite photonic crystal cavity[J]. Optics Letters, 2015, 40(17):4122–4125.
[7] OTSU N. A threshold selection method from gray-levelhistograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1):62–66.
[8]文山, 李葆青.基于小波分層的多方向图像边缘检测[J].自动化学报, 2007, 33(5):480–487.
[9] XIN L, SONG A G. A new edge detection method us-ing Gaussian-Zernike moment operator[C]// Proceedings of the 2nd International Asia Conference on Informatics in Control, Automation and Robotics. Wuhan, China: IEEE, 2010.
[10] LYVERS E P, MITCHELL O R, AKEY M L, et al.Subpixel measurements using a moment-based edge operator[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(12):1293–1309.
[11] LIAO S X, PAWLAK M. Image analysis with Zernikemoment descriptors[C]//Proceedings of the Canadian Conference on Electrical and Computer Engineering. Engineering Innovation: Voyage of Discovery. St. John's, Canada: IEEE, 1997.
[12] GHOSAL S, MEHROTRA R. Detection of compositeedges[J]. IEEE Transactions on Image Processing, 1994, 3(1):14–25.
[13]钱松, 李建荣.应用拉普拉斯算子设计高通滤波器进行图像增强分析[J].软件导刊, 2011, 10(12):158–159.
[14] HEROUT A, DUBSKÁ M, HAVEL J. Review ofHough transform for line detection[M]//HEROUT A, DUBSKÁ M, HAVEL J. Real-Time Detection ofLines and Grids. London: Springer, 2013:3−16.
[15] YORK D. Least-squares fitting of a straight line[J]. Ca-nadian Journal ofPhysics, 1966, 44(5):1079–1086.
[16] KRYSTEK M, ANTON M. A least-squares algorithmfor fitting data points with mutually correlated coordin- ates to a straight line[J]. Measurement Science and Technology, 2011, 22(3):035101.
[17]周聪, 谷付星.基于 CO2激光的微纳光纤熔接技术研究[J].光学仪器, 2019, 41(1):24–28.
(编辑:张磊)

