离轴抛物面的对比测量

陈巍　王青　朱贵博

摘要：采用离轴角度90°、口径1 inch 的离轴抛物面作为样品，比对了传统零位干涉测量结果和非接触式3D 非球面光学面形测量系统Luphoscan之间的差异。利用Zemax仿真了离轴抛物面六个维度的调整误差对测量结果的影响，分析了离轴量误差在两种完全不同测量过程中的表现形式，解决了Luphoscan测量结果可用性问题。根据仿真结果搭建动态干涉仪的零位检验干涉光路，建立了离轴抛物面的六个维度调节标准流程，可快速消除调整误差和离轴量误差，多次复现性测试结果达到了pv=0.135λ的精度。

关键词：离轴抛物面;无像差点法检测;Luphoscan;动态干涉仪

中图分类号： TN 206 文献标志码： A

Contrastive measurement of off-axis paraboloids

CHEN Wei，WANG Qing，ZHU Guibo

（School ofElectronic Engineering and Optoelectronic Technology， Nanjing University of Science and Technology， Nanjing 210094， China）

Abstract： An off-axis paraboloid with an off-axis angle of 45° and a diameter of 1 inch was used as the sample to compare the difference between the traditional null interferometric measurement results and the non-contact 3D aspheric optical surface shape measurement system Luphoscan. Zemax was used to simulate the influence of the adjustment errors of the six dimensions of the off- axis paraboloid on the measurement results. The expression of off-axis error in the two completely different measurement processes was analyzed， which solved the problem of the availability of Luphoscan measurement results. According to the  simulation results， the null test  interference optical path structure based on the dynamic interferometer was set up， and the six-dimensional adjustment  standard  process  of the  off-axis  paraboloid  was  established，  which  could  quickly eliminate the adjustment error and off-axis quantity error， and the repeatability test results reach the accuracy ofpv=0.135λ.

Keywords： off-axis paraboloid;stigmatic null test;Luphoscan;dynamic interferometer

引言

高精度的非球面光学元件在空间光学、空间激光通信、航空航天等领域发挥着重要的作用[1-3]。其中離轴非球面反射镜是先进光学系统朝着小型化和高性能方向发展必不可少的组成部分，其应用有效避免光学系统中心遮拦并改善相应的衍射问题提高成像质量，特别是其大离轴量反射镜增加了工作焦距和光路折转角度[4-5]。随着光学先进制造中数控加工技术的日益发展，制造的多个阶段均需要非球面的精密测量来指导和检验，对非球面检测提出了更高的要求。干涉测量中的零位检测法是非球面精密抛光阶段的主要测量方法，具有高分辨率、高准确度、高灵敏度以及重复性好等优点，已经过长期的使用和验证而获得广泛认同。而 Taylor Hobson 公司研制的Luphoscan是基于多波长干涉技术的非接触三维形貌点扫描测量系统，它能够实现高精度、非接触的光学元件面形测量，包括球面、非球面、自由曲面等。Luphoscan通过补偿系统，实现了对测量传感器的连续定位，并补偿了 R 、Z 及 T轴的机械误差，配合超高精度的多波长干涉传感器技术[6-7]，解决了单波长测量连续陡度较大区域的相位模糊问题，保证了在整个区域的精度优于50 nm。在实际应用中，Luphoscan的测量结果与干涉测量结果在平面、球面等简单函数表面测量中具有极好的符合性，而在非球面测量中出现了较大的差异[8-10]，如在测量旋转对称抛物面以及离轴抛物面时，测量结果都会出现不同程度的像散。本文通过无像差点法和Luphoscan测量系统对离轴抛物面进行了对比测量，分析了离轴量误差在两种测量过程中的表现形式，解决了Luphoscan测量结果的可用性问题，并建立了无像差点法测量离轴抛物面的调节标准流程，可快速消除调整误差和离轴量误差。

1 失调误差引入波像差的理论分析

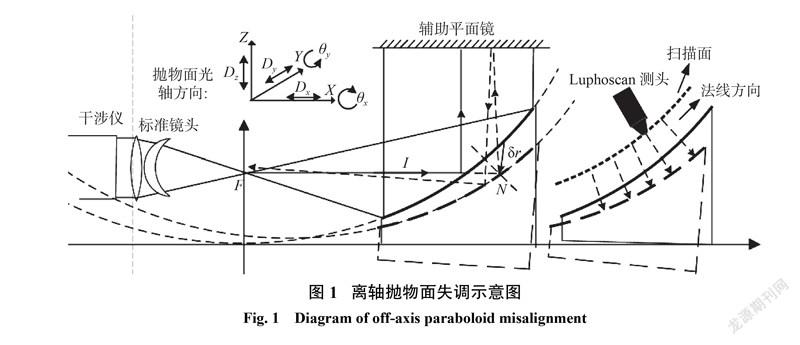
对于无像差点法检测离轴抛物面，如果抛物面处于理想位置，检测结果中仅包含元件面形误差，而抛物面任意维度与理想位置存在偏差时，测量结果中均会引入失调误差，失调示意图如图1所示。

图1中，干涉仪发出的平行光一部分经标准镜头会聚于共焦位置 F处，继续传播至抛物面上反射，最后经平面镜反射原路返回形成测试光，而另一部分经标准镜头参考反射面反射返回形成参考光，参考光与测试光发生干涉。无像差点法中测试光为非法线方向入射，而图1右半部分Luphoscan测量时探头始终垂直于待测件并作螺旋运动，即测试光均为法线方向入射。

无像差点法光路存在转折，存在干涉仪光轴方向和抛物面光轴方向，如图1中所示按抛物面的光轴方向定义坐标轴。旋转对称抛物面存在五个维度的调节，分别是沿着 X、Y、Z 轴的位移Dx 、 Dy 、Dz，以及分别绕着 X、Y轴的旋转  x 、 y ，根据单个光学表面偏心系统理论可知[11-12]，在存在Dx 、Dy 、Dz以及 x 、 y调整误差的情况下，抛物面母镜检测系统波像差公式为[13-15]

其中：δr为任意点的位移矢量; N为任意点的单位法向量; I 为入射光线的单位向量;被检离轴非球面母镜数学表达式为

其中： p2= x2+ y2表示母镜口径内任意点与几何中心的距离; c 为顶点曲率，则该面上任一点的单位法向量可表示为

根据位移矢量坐标关系有

将式（2）、（3）、（4）代入式（1），并将检测系统的光瞳从母镜变换到子镜，出瞳变换图如图2所示，子镜中心 O点到母镜中心 P点的X、Y方向距离分别为hx、hy，利用出瞳变换矩阵[16]，得到离轴抛物面检测系统波像差为

其中： r2= x2+ y2 ，即子镜上一点到中心 O 点的距离。由式（5）可知，对于离轴抛物面Dx 、Dy 、Dz、 x 、 y共同作用于彗差和像散项，并且像散项为主要误差项。

2 无像差点法的仿真与实验

2.1 无像差点法Zemax仿真

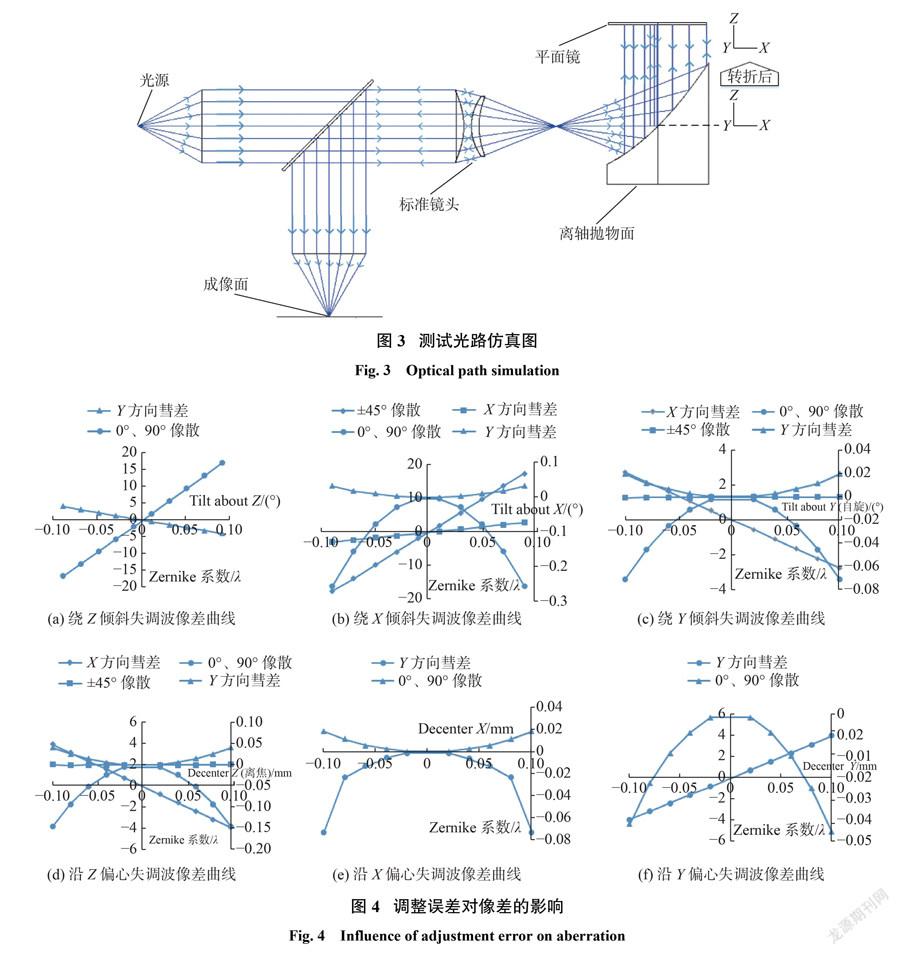
预先利用Zemax对离轴抛物面的无像差点法测量进行了仿真实验。采用会聚光入射的干涉腔布局方式，仿真测试光路图如图3所示。干涉仪模型为简化模型，标准镜头最后一个面为参考反射面，部分光束从该面反射返回形成参考光。在未添加任何调整误差时，干涉图为零条纹图，分别在各个维度添加少量调整误差，各维度的表述基于图3中转折后的坐标系，观察干涉图的变化以及 Zernike 彗差和像散项系数的变化，图4所示为各维度调整误差对像差的影响，其中：线性关系曲线对应中间的纵轴;非线性关系曲线对应右边的次纵轴。

图4中（a）、（b）、（c）、（d）、（e）、（f）分别为绕 Z倾斜、绕 X倾斜、绕 Y倾斜、Z 方向偏心、 X方向偏心、 Y方向偏心对像差系数的影响。由图4（a）和图4（b）看出，绕 Z 轴的倾斜和绕 X轴的倾斜主要分别产生了0°像散、45°像散，但图4（c）绕 Y轴的倾斜，即自旋方向，产生的主要是彗差;从图4（d）和图4（e）看出 Z 方向偏心（离焦）和 Y方向偏心主要分别产生了X方向彗差、 Y方向彗差，并且从图4（f）看到， X方向的偏心对像差的影响结果非常小。同时从图中可以看到较大的像差项与调整误差呈线性关系，而极小量的误差项与调整误差呈现二次方关系。

2.2 无像差點法实验

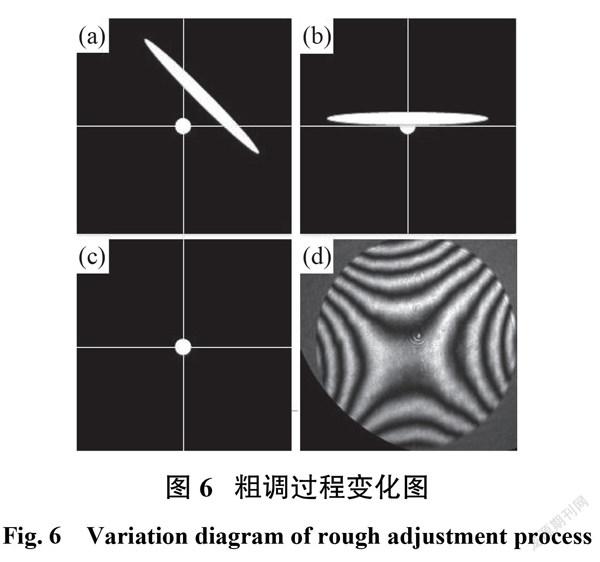
如图5所示为无像差点法测量离轴抛物面实物图，用到的元件有口径1 inch、离轴角度90°、焦距127 mm（离轴量）的抛物面， f/3的标准镜头、标准平晶，实验装置有新型动态干涉仪、二维调整架、五维调整架。图6所示为粗调过程光斑变化图，（a）、（b）、（c）、（d）分别对应每一步粗调后对应的光斑图。

实验步骤分为粗对准和精调两大步骤。实验中所用的新型动态干涉仪具有对点功能，方便粗对准过程的调节。粗对准的步骤：1）采用对点器观察离轴抛物面和平面反射镜形成的返回焦点聚焦光斑，需要与干涉仪会聚焦点重合，反射光斑此时会带有明显的随机离轴像散特点，即倾斜的长条光斑（图6（a）），在调整离焦的时候，出现两个方向长条光斑交替出现的现象;2）较大的离轴量通过平移/倾斜调整消除需要花费较多时间，因此第二步可以进行离轴抛物面的面内旋转，配合反射镜的二维倾斜调整，使得像散光斑的长条变短，方向达到横平竖直（图6（b））;3）通过调整动态干涉仪（或者离轴抛物面）单个方向（X或 Y）平移，并配合以平面反射镜的倾斜，使得光斑形状进一步变为圆形（图6（c））。粗对准完成后，干涉图也已基本变成圆形，干涉图存在明显的像散（图6（d）），此时的干涉图可以进行初步测试。接下通过波前测试结果进行精调，将测量模式设置为连续测量，可以实时动态检测到调节的结果。

精调的步骤：1）调节抛物面的 Z 方向平移和俯仰，将其称为一个调节对，或者调节抛物面的 Y方向平移和倾斜。例如可以尝试先调节 Z 方向使得干涉条纹变密、中心偏移，接着调节俯仰进行补偿，使得干涉条纹中心继续回到中央。观察测试结果的pv值或者像散项判断调节方向是否正确，像散项如果变大则往相反方向调节。重复此步骤，直到像散项值收敛，此时需要换抛物面的 Y方向平移和倾斜进行调节，同样重复上面的步骤。两个调节对的反复调节至收敛后，像散项基本上收敛至0.03个λ。2）精调抛物面的自旋维度，由于使用的是不带旋转的五维调整架，无法通过抛物面调节自旋，但可以调节动态干涉仪的 Y方向平移和俯仰在达到此目的，使得像散以及pv值进一步变小。3）此时的干涉图存在明显的离焦，调节动态干涉仪的 Z 方向离焦使得干涉条纹变直。适当调节抛物面的Z 方向平移或者 Y方向平移，使得干涉条纹数目变少接近至零条纹。

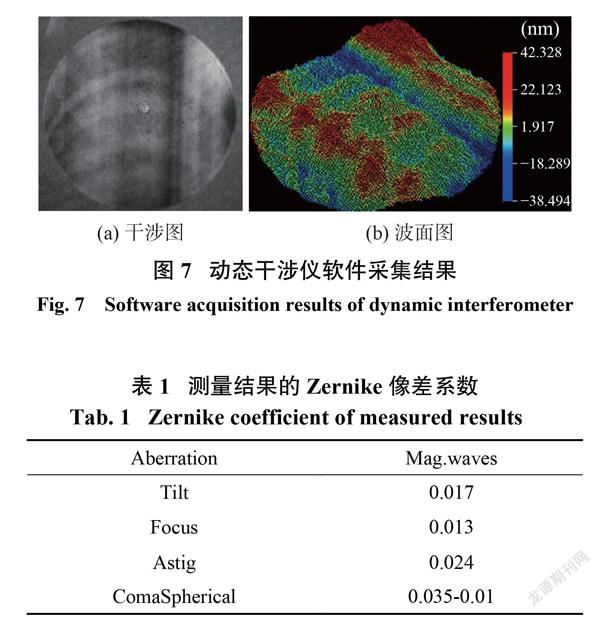
采集数据，进行消常数项、倾斜项和离焦项处理，图7（a）为干涉图，7（b）为波面图，表1为测量结果 Zernike 系数前几项，测量结果pv=0.137λ，像散项Astig=0.024λ，多次重复性测量结果pv的均方根值为pv=0.135λ。测量结果包含了标准镜头的误差和平面镜的误差，标准平晶的pv值优于1/40λ，标准镜头pv值优于1/20λ，该干涉条纹图将近零条纹，离轴量误差与调整误差均已消除掉，可直接分辨出抛物面的表面形貌，对比解包后的波面图，均能明显看到抛物面加工留下的车痕。

3  Luphoscan测量离轴抛物面

Luphoscan作为轮廓测量仪的一种，测量面形误差的原理是通过在理论坐标系中测量实点的坐标，然后与理论坐标相比较计算获得面形误差。Luphoscan在测量离轴抛物面时需要将母镜曲率半径、离轴角度、口径、测量分辨率等参数输入到离轴抛物面的 sag 表计算软件中，得到该离轴抛物面的理论设计点云。

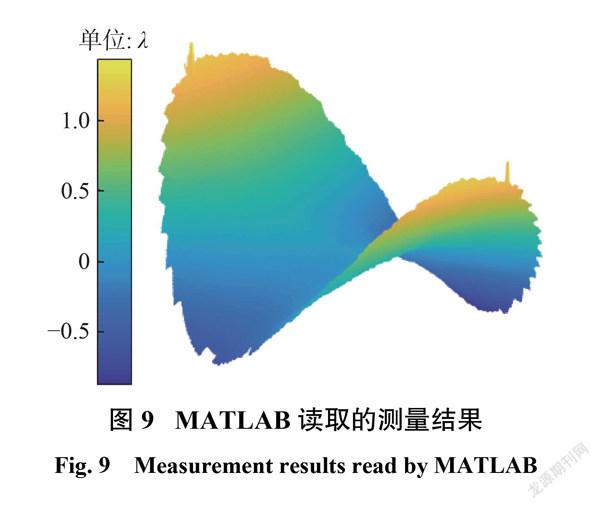
理想情况下测量坐标系 X轴为离轴位置处的切线， Y轴通过该离轴处的坐标。Luphoscan测量里离轴抛物面的情形如图8所示，利用配置的工装水平夹持住离轴抛物面。由于离轴抛物面 Y方向的对称性很容易将 Y方向的倾斜与偏心误差调整掉，接着粗调 X方向的倾斜，通过测量离轴抛物面小区域的 sag 值的方式精调X方向的倾斜和偏心误差，直至 sag 与理论设计相吻合，但是实际抛物面存在离轴量误差，使得 X方向调平、调心后依然存在偏心和倾斜误差。随后探头沿着理论设计的曲线做螺旋运动，始终垂直于测量表面，依次测量各个点的实际偏差值，即离散的离轴抛物面面形数据。测量结果如图9所示，所包含的额外误差是离轴量误差直接或间接引入的，简单地通过 Zernike 多项式拟合消像散无法得到实际的面形。

无像差点法测量的是实际离轴量下的面形参数，假设干涉仪测量出来的数据是理想的绝对面形，测量结果记为Win，实际离轴量的离轴抛物面矢高分布记为S ac，则（Win+ S ac）即为世界坐标上的矢高值，同时根据干涉仪的 CCD 像素大小可以计算获得世界坐标的 X分量和 Y分量;将 X轴方向倾斜角误差记为 y，偏心误差记为d，故有倾斜和偏心的点云数据，如式（6）所示

将式（6）的点云数据拟合成曲面，运用合适的算法计算理论设计点云的每个点到该曲面的垂直距离，将该过程记为映射 G，最终的Luphoscan测量数据记为WLu，则存在如下关系

最后，对Luphoscan测量与干涉仪的测量比对如表2所示。

4 结论

本文采用传统无像差点法和Luphoscan对离轴抛物面进行了对比测量，无像差点法测量结果无明显像差，而Luphoscan测量结果存在明显像散项。无像差点法检测离轴抛物面时，调节抛物面姿态时，总是会朝着减小彗差和像散项的方向调节，而离轴量误差可以看作是 X方向和 Z方向偏心误差的叠加，必然会引入像散和彗差。实验调节过程中，人为将离轴量误差视为调整误差将其调整消除，故传统的无像差点法测量方式无法检测到离轴量误差，但是该测量方式可以精密测量实际离轴量的抛物面。由于Luphoscan在测量时沿着理论设计曲线做螺旋运动，测量的是理论值与实际的偏差，故最终测量的结果包含了离轴量误差，解决了Luphoscan测量结果的可用性问题，后续可通过分析其中像差项逆推求取离轴量误差，恢复实际离轴抛物面的绝对测量。

参考文献：

[1]张元芫， 刘海勇.基于非球面透镜组激光光束整形设计[J].中国新技术新产品， 2018（3）：12–14.

[2]宋志化， 江伦， 曹海帅， 等.非球面整形镜在空间激光通信终端中的应用[J].激光与光电子学进展， 2018， 55（10）：76–81.

[3]孟晓辉， 王永刚， 李文卿.航天相机非球面光学元件的离子束抛光工艺研究[J].航天制造技术， 2016（6）：27–31.

[4]李志来， 薛栋林， 张学军.长焦距大视场光学系统的光机结构设计[J].光学精密工程， 2008， 16（12）：2485–2490.

[5]朱凡， 李颖先， 谭久彬.高精度激光光束准直系统设计[J].光学精密工程， 2020， 28（4）：817–826.

[6] BERGER G， PETTER J. Non-contact metrology of as-pheric  surfaces  based  on  MWLI  technology[C]//Pro-ceedings  of  SPIE 8884，  Optifab 2013. New  York： SPIE， 2013：88840V.

[7] WENDEL M. Measurement of small optics by use of amulti-wavelength  interferometrical  approach[C]//Pro- ceedings of SPIE 11385， Optics and Measurement  In- ternational  Conference 2019. Liberec： SPIE， 2019：113850M.

[8] WENDEL M. Measurement of freeforms and complexgeometries by  use  of tactile profilometry  and  multi- wavelength  interferometry[C]//Proceedings  of  SPIE 11171，  Sixth  European  Seminar  on  Precision  OpticsManufacturing. Teisnach： SPIE， 2019：1117109.

[9] STOVER E， BERGER G， WENDEL M， et al. Fast op-tical 3D form measurement of aspheresincluding  de- termination of thickness  and wedge  and decenter  er- rors[C]//Proceedings of SPIE 9633， Optifab 2015. New York： SPIE， 2015：96331O.

[10] BERGER G， WENDEL M. Optical metrology of free-forms and complex lenses：3D form measurements of precision optical surfaces based on scanning point  in- terferometry[J]. Optik&Photonik， 2018， 13（1）：40–43.

[11] RIMMER  M. Analysis  of perturbed  lens  systems[J].Applied Optics， 1970， 9（3）：533–537.

[12] WETHERELL W B， RIMMER M P. General analysisof aplanatic Cassegrain， Gregorian， and Schwarzschildtelescopes[J]. Applied  Optics， 1972， 11（12）：2817–2832.

[13]車驰骋， 李英才， 樊学武， 等.基于矢量波像差理论的计算机辅助装调技术研究[J].光子学报， 2008， 37（8）：1630–1634.

[14]樊学武， 陈荣利， 马臻， 等.偏心和倾斜光学系统初级象差理论的研究[J].光子学报， 2004， 33（4）：494–496.

[15]杨新军， 王肇圻， 母国光， 等.偏心和倾斜光学系统的像差特性[J].光子学报， 2005， 34（11）：1658–1662.

[16]陈钦芳， 李英才， 马臻， 等.离轴二次非球面反射镜无像差点法检测的误差分离技术[J].光学学报， 2011，31（2）：0222001.

（编辑：钱紫衡）