基于硅透镜与光子晶体的逆古斯汉欣位移监测系统及其温度特性研究
汤大卫 梁斌明 季景
摘要:基于硅介质柱型光子晶体,采用时域有限差分方法(FDTD),探究高斯光束在光子晶体界面的逆古斯汉欣(GH)位移。通过在光子晶体下表面添加硅透镜,研究高斯光束的入射角度、硅透镜的曲率半径以及温度对光子晶体逆 GH 位移的影响。研究结果表明,发生最大逆 GH 位移的角度大于几何理想全反射角。添加焦点位于光子晶体表面中心的硅透镜可以使逆 GH 位移显著增强,且当硅透镜的曲率半径为170时,逆 GH 位移增大为不加透镜时的1.7倍。研究不同入射角度下温度对光子晶体的逆 GH位移的影响发现,当高斯光束的入射角为26º时,逆 GH 位移随着温度的变化最大且线性度较好,便于温度监测。
关键词:光子晶体;逆古斯汉欣位移;硅透镜
中图分类号: O 438 文献标志码: A
Study on the inverse Goos-Hanchen shift monitoring systembased on silicon lens and photonic crystal andits temperature characteristics
TANG Dawei,LIANG Binming,JI Jing
(School of Optical-Electrical and Computer Engineering, University of Shanghai forScience and Technology, Shanghai 200093, China)
Abstract: Based on the silicon dielectric cylindrical photonic crystal, the finite-difference time- domain (FDTD) method is used to investigate the inverse Goos-Hanchen (GH) shift of Gaussian beam at the photonic crystal interface. By adding a silicon lens on the lower surface of the photonic crystal, the influence of the incident angle of Gaussian beam, the curvature radius of the silicon lens and the temperature on the inverse GH shift of the photonic crystal is studied.The results show that the maximum inverse GH shift angle is larger than the geometric ideal total reflection angle. The addition of a silicon lens with the focus in the center of the photonic crystal surface cansignificantly enhance the inverse GH shift. When the curvature radius of the silicon lens is 170, the inverse GH shift increases by 1.7 times as much as that without the lens. The influence of temperature on the inverse GH shift of photonic crystal at different incident angles is studied. It is found that when the incident angle of Gaussian beam is 26 degrees, the inverse GH shift has a wide range of variation with temperature, and the linearity of variation curve is better, which is convenient for temperature monitoring.
Keywords: photonic crystal;inverse Goos-Hanchen shift;silicon lens
引言
光束在兩种介质分界面发生全反射时,实际的反射光束相对于理论几何光学反射光束会产生一段微小的位移,该位移就被称作古斯汉欣(GH)位移。1947年,Goos和Hanchen两位研究者[1]利用光的多次反射实验证实了光束在两界面处发生全反射时,反射点和入射点之间发生的相位突变会导致界面上出现纵向位移。入射光线由光密介质穿射透入光疏介质时,会沿两物质分界面方向传播一定的距离,实际上该光线相当于振幅呈指数递减的倏逝波,倏逝波在接近全反射或者达到全反射时达到最大振幅。1948年,Artmann[2]通过稳态相位法对 GH位移做出了理论解释:实际的入射光束并不是理想的平面波,可以看作是一系列波矢方向有轻微差异的单色平面波的叠加,在发生全反射时,不同波矢方向的分量产生的位移都不一样,最后这些反射平面波的分量叠加形成实际的反射光束,反射光相对于入射光会出现一个纵向的微小位移。介电常数"和磁导率是决定电磁波在物质中传播的基本特征量,1968年,Veselago[3]在他的研究中提出:当电磁波在"和都为负值的左手材料中传播时,会发生逆 GH位移现象和反常多普勒效应。随着负折射率材料的发现以及光子晶体的广泛应用[4-14],学者们逐渐深入研究这两个方向的 GH 位移。2003年, Felbacq等[15]探讨了 GH 位移在光子晶体禁带上的情况;Shadrivov等[16]研究了负折射率材料上的 GH 位移。2006年, He 等[17]对二维光子晶体界面的逆 GH位移进行了探究,并基于时域有限差分法(FDTD)对反射光的逆 GH位移进行了研究。2015年, Luo 等[18]在红外波段的棱镜−波导耦合系统结构上研究了温度对 GH位移的影响,为温度调制器的灵敏性设计提供帮助。2016年,陆志仁课题组[19] 研究了近零折射率材料中 GH 位移的影响因素,研究表明,波长对 GH位移有非常大的影响,温度对 GH 位移影响较小。2017年, Jiang 等[20]对 TE 和 TM 偏振光入射光子晶体时反射光的 GH 位移进行研究,研究发现 TE偏振光的反射光的 GH 位移为负,而 TM 光的 GH 位移为正。2020年,曹振洲等[21]研究了不同波长的偏振光在狄拉克半金属(DSM)上的 GH位移,并提出:通过电调谐 DSM 的费米能量,可以改变介电函数和 GH 位移;反之, GH 位移可以用来检测能量。
本文利用高斯光束的发散效应,在负折射光子晶体下表面放置硅凸透镜,着重探究不同高斯光束的入射角度、硅透镜的曲率半径以及环境温度对光子晶体逆 GH位移的影响。陆志仁等[19]对光子晶体的 GH 位移研究中,环境温度对 GH 位移的影响较小,而本文研究的光子晶体结构中,环境温度对光子晶体的逆 GH位移的影响较大。据此可以在光子晶体实验中实时探测光子晶体器件温度变化,为相关光子晶体实验中研究温度影响提供方便。本文采用与光子晶体同样介质的硅透镜,易于集成,减小了采用分立透镜对焦的误差影响,更便于实际加工。
1 仿真设计
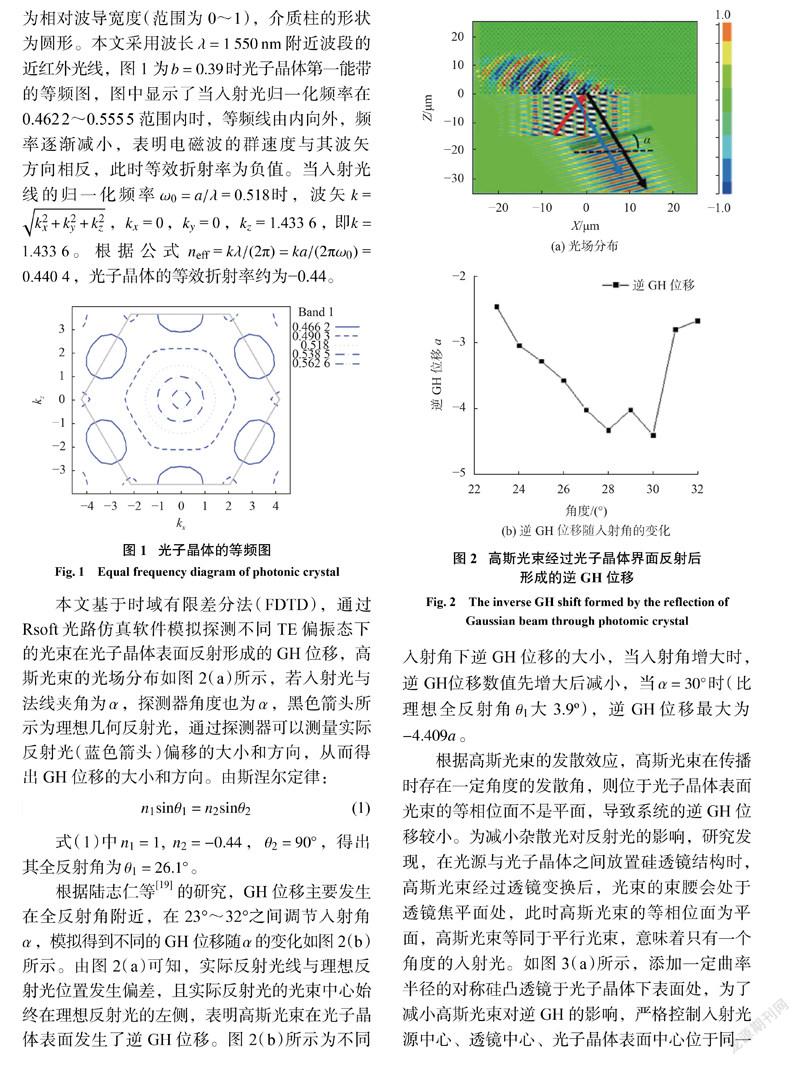
本文是以空气作为基底,硅介质柱型作为二维光子晶体的平板结构。其中,硅的折射率n =3:5,R =2r = b · a,其中晶格常数a =775 nm ,b为相对波导宽度(范围为0~1),介质柱的形状为圆形。本文采用波长 =1550 nm 附近波段的近红外光线,图1为b =0:39时光子晶体第一能带的等频图,图中显示了当入射光归一化频率在0.4622~0.5555范围内时,等频线由内向外,频率逐渐减小,表明电磁波的群速度与其波矢方向相反,此时等效折射率为负值。当入射光线的归一化频率!0= a==0.518时,波矢 k = k + k + k ,kx =0,ky =0,kz =1.4336,即k =1.4336。根据公式neff = k =(2π)= ka=(2π!0)=0.4404,光子晶体的等效折射率约为−0.44。
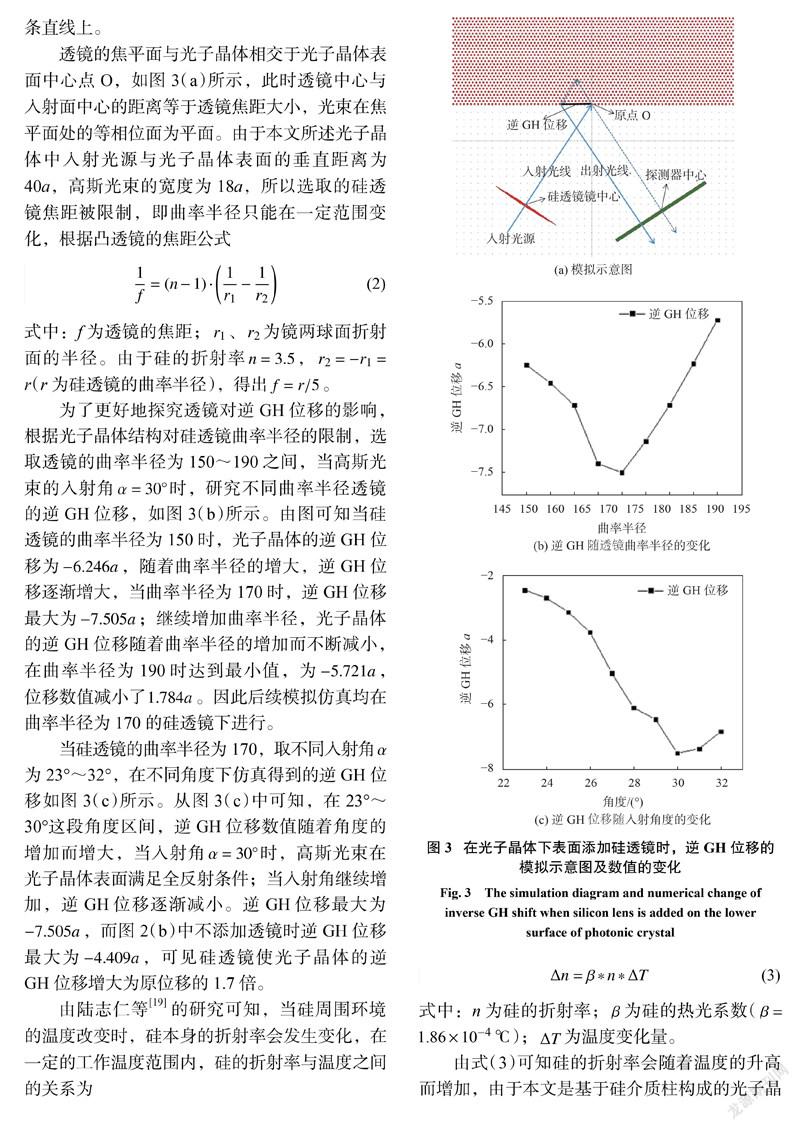
本文基于时域有限差分法( FDTD),通过Rsoft光路仿真软件模拟探测不同 TE 偏振态下的光束在光子晶体表面反射形成的 GH位移,高斯光束的光场分布如图2(a)所示,若入射光与法线夹角为,探测器角度也为,黑色箭头所示为理想几何反射光,通过探测器可以测量实际反射光(蓝色箭头)偏移的大小和方向,从而得出 GH 位移的大小和方向。由斯涅尔定律:
式(1)中 n1=1 , n2=−0:44,2 =90◦,得出其全反射角为1=26:1◦。
根据陆志仁等[19]的研究, GH 位移主要发生在全反射角附近,在23°~32°之间调节入射角,模拟得到不同的 GH位移随的变化如图2(b)所示。由图2(a)可知,实际反射光线与理想反射光位置发生偏差,且实际反射光的光束中心始终在理想反射光的左侧,表明高斯光束在光子晶体表面发生了逆 GH位移。图2(b)所示为不同入射角下逆 GH位移的大小,当入射角增大时,逆 GH位移数值先增大后减小,当 =30◦时(比理想全反射角1大3.9º),逆 GH 位移最大为−4:409a 。
根据高斯光束的发散效应,高斯光束在传播时存在一定角度的发散角,则位于光子晶体表面光束的等相位面不是平面,导致系统的逆 GH位移较小。为减小杂散光对反射光的影响,研究发现,在光源与光子晶体之间放置硅透镜结构时,高斯光束经过透镜变换后,光束的束腰会处于透镜焦平面处,此时高斯光束的等相位面为平面,高斯光束等同于平行光束,意味着只有一个角度的入射光。如图3(a)所示,添加一定曲率半径的对称硅凸透镜于光子晶体下表面处,为了减小高斯光束对逆 GH 的影响,严格控制入射光源中心、透镜中心、光子晶体表面中心位于同一条直线上。
透镜的焦平面与光子晶体相交于光子晶体表面中心点 O,如图3(a)所示,此时透镜中心与入射面中心的距离等于透镜焦距大小,光束在焦平面处的等相位面为平面。由于本文所述光子晶体中入射光源与光子晶体表面的垂直距离为40a ,高斯光束的宽度为18a ,所以选取的硅透镜焦距被限制,即曲率半径只能在一定范围变化,根据凸透镜的焦距公式
式中: f 为透镜的焦距; r1、r2为镜两球面折射面的半径。由于硅的折射率n =3:5, r2=−r1= r(r为硅透镜的曲率半径),得出 f = r=5。
为了更好地探究透镜对逆 GH位移的影响,根据光子晶体结构对硅透镜曲率半径的限制,选取透镜的曲率半径为150~190之间,当高斯光束的入射角 =30◦时,研究不同曲率半径透镜的逆 GH位移,如图3(b)所示。由图可知当硅透镜的曲率半径为150时,光子晶体的逆 GH位移为−6:246a ,随着曲率半径的增大,逆 GH位移逐渐增大,当曲率半径为170时,逆 GH位移最大为−7:505a ;继续增加曲率半径,光子晶体的逆 GH位移随着曲率半径的增加而不断减小,在曲率半径为190时达到最小值,为−5:721a ,位移数值减小了1:784a 。因此后续模拟仿真均在曲率半径为170的硅透镜下进行。
当硅透镜的曲率半径为170,取不同入射角为23°~32°,在不同角度下仿真得到的逆 GH位移如图3(c)所示。从图3(c)中可知,在23°~30°这段角度区间,逆 GH位移数值随着角度的增加而增大,当入射角 =30◦时,高斯光束在光子晶体表面满足全反射条件;当入射角继续增加,逆 GH 位移逐渐减小。逆 GH 位移最大为−7:505a ,而图2(b)中不添加透镜时逆 GH位移最大为−4:409a ,可见硅透镜使光子晶体的逆GH 位移增大为原位移的1.7倍。
由陆志仁等[19]的研究可知,當硅周围环境的温度改变时,硅本身的折射率会发生变化,在一定的工作温度范围内,硅的折射率与温度之间的关系为
式中: n 为硅的折射率;为硅的热光系数( =1.86×10−4℃);∆T为温度变化量。
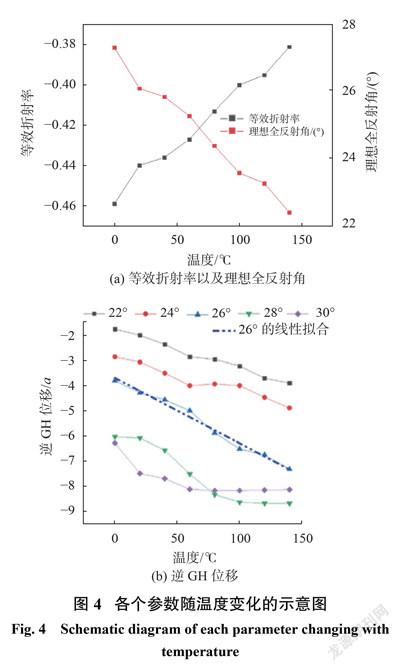
由式(3)可知硅的折射率会随着温度的升高而增加,由于本文是基于硅介质柱构成的光子晶体,因此整个光子晶体的等效折射率也会受到温度影响(上述研究均在室温20℃下进行)。在不同温度下研究光子晶体的等效折射率以及光子晶体的理想全反射角随温度的变化情况,如图4(a)所示,当温度增加时,光子晶体的等效折射率增加,温度为0℃时等效折射率为−0.459,140℃时等效折射率增加到−0.381;由于光子晶体的等效折射率小于零,其理想全反射角随着等效折射率增大而减小,当温度从0℃增加到140℃时,理想全反射角由27.32º减小到22.4º,这意味着系统发生最大逆 GH位移的角度逐渐减小。
由图1(b)可知高斯光束的入射角度对逆 GH 位移的影响较大,当波长=1:9305a 时, 在22º~30º之间调节高斯光束的入射角,进而研究光子晶体的逆 GH位移与温度的变化关系。如圖4(b)所示,通过仿真发现,相同温度条件下,随着入射角的增大直至满足全反射条件的入射角时,逆 GH位移不断增大。但随着温度大于80℃,为28º时已经达到相应等效折射率对应的全反射条件,因此为30º时逆 GH位移反而减小。当入射角 =28◦时,逆GH位移在0~100℃区间内逐渐增加(增加了2.305a),当温度为100℃时,其理想全反射角为2=23.6◦,满足全反射条件,所以温度从100℃继续增加,逆 GH位移保持不变。当入射角=30◦时也是同样原因,因此为28º和30º时,曲线偏离了线性。
上述仿真模拟结果表明:光子晶体工作温度对逆 GH位移的影响程度与高斯光束的入射角度有关。当入射角 =30◦且温度高于60℃时,光束始终满足全反射条件,其逆 GH位移不受温度影响;当入射角 =28◦且温度高于100℃时,系统的逆 GH位移保持不变;当入射角为22º~26º时,逆 GH位移随着温度的增加而增大。其中入射角 =26◦时,其逆 GH 位移受温度影响范围最大且线性度较好。图4(b)中蓝色点划线为 =26◦时的拟合线,其方程表达式为: y =−0:02601x −3:70733a ,拟合优度为0.98469,实际仿真中温度从0℃到140℃时逆 GH位移增加了3.64a。
2 结论
本文基于 FDTD 探究高斯光束在硅介质柱型光子晶体界面的逆 GH位移。研究表明,在负折射率光子晶体下表面添加一定曲率半径的硅透镜且焦点与光子晶体表面中心重合时,光子晶体的逆 GH位移显著增加。探究不同入射角度下温度对逆 GH位移的影响发现,当 =26◦时逆 GH 位移的变化范围最大且线性度较好。本研究可以在光子晶体实验中实时探测光子晶体器件温度变化,从而为相关光子晶体实验进行温度影响研究提供方便。
参考文献:
[1] GOOS F, HÄNCHEN H. Ein neuer und fundamentalerversuchzurtotalreflexion[J]. Annalen derPhysik, 1947, 436(7/8):333–346.
[2] ARTMANN K. Berechnungder seitenversetzung destotalreflektiertenstrahles[J]. Annalen der Physik, 1948,437(1/2):87–102.
[3] VESELAGO V G. The electrodynamics of substanceswith simultaneously negative values of ε and μ[J]. So- viet Physics Uspekhi, 1968, 10(4):509–514.
[4]刘少斌 , 朱传喜 , 袁乃昌.等离子体光子晶体的FDTD 分析[J].物理学报, 2005, 54(6):2804–2808.
[5] CHEN Y L, FANG Y T. Imaging inside photonic crys-tal slab using negative refraction[J]. Lasers in Engineer- ing, 2014, 16(3/4):325–332.
[6] ALIPOUR-BANAEI H, SEIF-DARGAHI H. Photoniccrystal based 1-bit full-adder optical circuit by using ring resonators in a nonlinear structure[J]. Photonics and Nanostructures - Fundamentals and Applications, 2017, 24:29–34.
[7] KE X Z, WANG S S. Design of photonic crystal fibercapable of carrying multiple orbital angular mo- mentum modes transmission[J]. Optics and Photonics Journal, 2020, 10(4):49–63.
[8] PASTUR L A, SLAVIN V V, YANOVSKII A V. Onballistic transport in channels with negative refraction of particles[J]. Low Temperature Physics, 2018, 44(7):711–717.
[9]牛金科, 梁斌明, 庄松林, 等.二维光子晶体双重亚波长成像[J].光电工程, 2019, 46(8):66–72.
[10] XIA M D, TIAN X X, QU S B. A microwave absorb-ing material with soft magnetic nanoparticles based on negative refraction loss characteristics[J]. The Interna- tional Journal of Electrical Engineering & Education, 2019, 56(4):305–314.
[11]高伦, 梁斌明, 王婷, 等.光子晶体负折射效应的电光偏转器[J].光电工程, 2016, 43(5):77–81.
[12] LU G Z, ZHAO R Q, YIN H C, et al. Selective absorp-tion of photonic crystal with graphene[J]. Plasmonics,2020, 15(2):475–479.
[13] LAN S F, KANG L, SCHOEN D T, et al. Backwardphase-matching for nonlinear optical generation in neg- ative-index materials[J]. Nature Materials, 2015, 14(8):807–811.
[14]胡金兵, 陈家璧, 庄松林.不同材料逆古斯汉欣位移机理的对比研究[J].上海理工大学学报, 2016, 38(3):271–275.
[15] FELBACQ D, MOREAU A, SMAÂLI R. Goos-Hänchen effect in the gaps of photonic crystals[J]. Op- tics Letters, 2003, 28(18):1633–1635.
[16] SHADRIVOV I V, ZHAROV A A, KIVSHAR Y S.GiantGoos-Hänchen effect at the reflection from left- handed metamaterials[J]. Applied Physics Letters, 2003, 83(13):2713–2715.
[17] HE J L, YI J, HE S L. Giant negative Goos-Hänchenshifts for a photonic crystal with a negative effective in- dex[J]. Optics Express, 2006, 14(7):3024–3029.
[18] TANG T T, LUO L, LIU W L, et al. Thermo-opticGoos-Häncheneffect in silicon-on-insulator wave- guide[J]. Applied Physics B, 2015, 120(3):497–504.
[19]陆志仁, 梁斌明, 丁俊伟, 等.近零折射率材料的古斯汉欣位移的特性研究[J].物理学报, 2016, 65(15):154208.
[20] JIANG Q, CHEN J B, LIANG B M, et al. Direct meas-urement of the negative Goos-Hänchen shift of single reflection in a two-dimensional photonic crystal with negative refractive index[J]. Optics Letters, 2017, 42(7):1213–1216.
[21]曹振洲, 肖之偉, 王国飞.狄拉克半金属中电调谐古斯-汉欣位移(英文)[J].中南民族大学学报:自然科学版, 2020, 39(3):277–282.
(编辑:张磊)

