测度链上分数阶动力方程的最优控制问题

任秋艳, 杨巧玲

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州财经大学 信息工程学院， 甘肃 兰州 730020)

1990年,德国学者Hilger发表了其有关测度链理论的论文[1]. 这一新的理论在离散分析和连续分析之间建立了一座桥梁,使人们可以同时处理离散和连续系统,分析其异同点,这样就避免了对很多问题的两次重复研究.同时,因为测度链除了包含实数集和整数集之外还包含其它一些集合,因而可以得到更为广泛的结果.

近年来,测度链上的最优控制问题因其具有广泛的应用背景而备受人们的关注.例如,Bartosiewicz等[2]、Ferreira等[3]、Hilscher等[4]、Malinowska等[5]讨论了测度链上的变分问题,Stehlik等[6]、Hilscher等[7]、Zhou等[8]、Bohner等[9]考虑了测度链上的最大值原理,而Liu等[10]、Carlson[11]、Lavrova[12]、Sun等[13]研究了测度链上最优控制问题最优解的存在性和最优的必要条件.虽然在测度链上最优控制问题方面已经取得了一定的研究成果,但是他们讨论的控制系统都是由测度链上整数阶动力方程构成的.

分数阶微分方程是整数阶微分方程的拓展,它具有深刻的物理背景和丰富的理论内涵,现在已应用于混沌与湍流、控制理论、物理化学、随机过程、粘弹性力学与非牛顿流体学等许多科学领域.近来,分数阶最优控制问题受到人们的高度重视[14-19].

本文总是假设T是一个测度链(实数集R的任意一个非空闭子集),T>0固定,0,T∈T,σ(T)=T且Uad表示容许控制集.对于R中的任意子区间I,定义IT=I∩T.

对于任意给定的控制策略u∈Uad,本文讨论的控制系统是下述测度链T上的非线性分数阶动力方程初值问题

(1)

通过给f和g一些合适的条件,对于任意给定的控制策略u∈Uad,获得了非线性分数阶控制系统(1)唯一解的存在性.研究测度链上的最优控制问题(P):找一个u0∈Uad,使得

J(u)≥J(u0)u∈Uad

其中

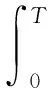
u∈Uad

是二次型性能指标,其中xu是非线性分数阶控制系统(1)相应于控制策略u的解且xd是期望值.

1 预备知识

给出本文需要的有关测度链及测度链上分数微积分的一些基本的定义和引理,详细的内容可参考文献[20-23].

定义1对于t∈T,定义向前跳跃算子σ:T→T为

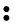
定义向后跳跃算子ρ:T→T为

在这个定义中,令inf ∅=supT以及sup ∅=infT,其中∅表示空集.如果σ(t)>t,则称t是右稀的;如果ρ(t)infT且ρ(t)=t,则称t是左稠的.T的子集Tk定义为如果T有左稀的最大值m,则Tk=T-{m},否则,Tk=T.函数μ:T→[0,+∞)定义为

定义2设f:T→R且t∈Tk,如果存在一个实数θ,使得对于任意的ε>0,存在t的一个开领域U(U=(t-δ,t+δ)T,δ>0),使得对于所有的s∈U,都有

|f(σ(t))-f(s)-θ(σ(t)-s)|≤ε|σ(t)-s|

成立,则称f在t点是Δ-可微的,θ被称为f在t点的Δ-导数,记为θ=fΔ(t).若对于所有的t∈Tk,f在t点都是Δ-可微的,则称f在Tk上是Δ-可微的.

定义3设F和f:T→R是两个函数,如果对于所有的t∈Tk,

FΔ(t)=f(t)

则称F是f的一个原函数.此时,定义f的Cauchy积分为

定义4设0<α<1,[a,b]T上α阶的Riemann-

其中Γ是Gamma函数.

引理2[22]设α>0,β>0且h是[a,b]T上的Δ-可积函数,则

引理3[22]设f是[a,b]T上的连续递增函数,如果f的延拓F定义为

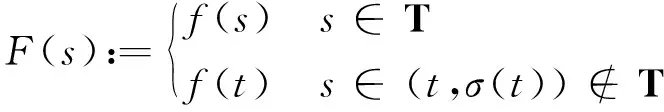
则

本文的工具是下面的定理.

定理1[24](Banach压缩映射原理) 设(X,d)是完备的距离空间且Φ:X→X是压缩映射，则Φ在X中有唯一的不动点.

2 主要结果

记C([0,T]T,R)={x|x:[0,T]T→R是连续函数},赋予其范数为

则C([0,T]T,R)是Banach空间.

引理4对于任意给定的y∈C([0,T]T,R),测度链上的分数阶动力方程初值问题

(2)

有唯一解

t∈[0,T]T

证明因为

所以由引理2可知：

x(t)-x(0)t∈[0,T]T

从而,由式(2)可得

t∈[0,T]T

首先,列出后面要用到的条件:

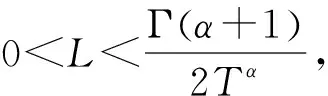
(A2)g:R→R且存在K>0,使得

|g(ω)-g(v)|≤K|ω-v|,ω,v∈R

假设控制空间是C([0,T]T,R)且容许控制集Uad是C([0,T]T,R)中的紧子集.

引理5假设(A1)和(A2)成立,则对于任意给定的控制策略u∈Uad,非线性分数阶控制系统(1)有唯一解xu且

证明对于任意固定的u∈Uad,定义算子Φu:C([0,T]T,R)→C([0,T]T,R)为

显然,Φu的不动点即为非线性分数阶控制系统(1)的解.

对于任意固定的t∈[0,T]T,由引理3易知：

(3)

令x,y∈C([0,T]T,R),则根据式(3)和(A1)可得

这表明

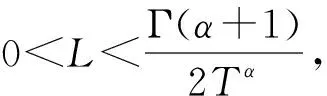
定理2假设(A1)和(A2)成立,则最优控制问题(P)存在一个最优解u0∈Uad.

证明首先,由引理5可知,对于任意给定的控制策略u∈Uad,非线性分数阶控制系统(1)有唯一解xu且

其次,因为

u∈Uad

(4)

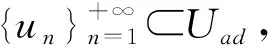
(5)

另一方面,由(A1),(A2)和式(3)可知,对于任意的n=1,2,…,

|xun(t)-xu0(t)|=

f(s,xu0(s),xu0(σ(s)))+

f(s,xu0(s),xu0(σ(s)))|+

|g(un(s))-g(u0(s))|]Δs≤

|xun(σ(s))-xu0(σ(s))|]+

K|un(s)-u0(s)|}Δs≤

t∈[0，T]T

这表明

n=1,2,…

(6)

从而,由式(5)和式(6)可得

(7)

于是,由引理1,式(5)和式(7)可知：

再根据式(4)可得

因此,对于所有的u∈Uad,都有J(u)≥J(u0).这表明u0是最优控制问题(P)的一个最优解.

3 结论

本文考虑了一类测度链上非线性分数阶动力方程的最优控制问题.通过给相关函数适当的条件,对于任意给定的控制策略,获得了非线性分数阶控制系统唯一解的存在性.所用的工具是Banach压缩映射原理.证明了最优控制问题在容许控制集中存在一个最优解.