基于有限元计算的全陶瓷微封装燃料芯块等效热导率与微结构设计

张旭东, 邓俊楷, 马大衍, 曹慧颖, 张瑞谦, 唐 睿

(1. 西安交通大学 金属材料强度国家重点实验室, 陕西 西安 710049; 2. 西安交通大学 网络信息中心, 陕西 西安 710049; 3. 中国核动力研究设计院 反应堆燃料及材料重点实验室， 四川 成都 610213)

全陶瓷微封装燃料(FCM)芯块是一种新型的事故容错燃料，也是典型的多相复合材料，由 SiC 基体和分散其中的TRISO颗粒组成[1].TRISO颗粒具有多层包覆结构，一般为5层，从内到外依次为核心燃料UO2层，缓冲碳层Buffer 层、致密热解碳层IpyC层、SiC层和致密热解碳层OpyC层.TRISO颗粒各包覆层的作用都不尽相同.整体上，TRISO 颗粒的多层包覆结构为裂变产物提供了非常大的容纳空间和缓冲作用.因此，TRISO燃料颗粒弥散于SiC基体中形成的FCM核燃料芯块也表现出良好的结构稳定性和裂变产物容纳性能，成为事故容错燃料的主要研究方向之一[2-5].

FCM芯块作为典型的复合材料，TRISO颗粒的含量、分布等对其热导率均有较大影响[6-7].另一方面，TRISO颗粒作为特殊的分层多相结构，其包覆层结构也会影响颗粒整体的热导率，进而影响FCM芯块的热导率[8].有诸多学者利用有限元方法开展了相关研究.例如，Liu等[9]利用有限元模拟对比研究了多种TRISO颗粒分布对FCM芯块中最大温度的影响.Wei等[10]提出了FCM燃料芯块中多孔碳材料有效导热模型的有限元模型.Li等[11]利用有限元方法研究了正常运行条件下压水堆(PWR)燃料棒中两层SiC包覆层的热力学行为.目前对于分层TRISO颗粒，以及由TRISO颗粒与SiC基体构成的FCM芯块复合结构，其有效热导率均缺乏有效的计算模拟方法，制约了FCM芯块的结构设计与优化.

为解决上述问题，采用有限元方法，利用开源有限元程序CalculiX[12]实现球体法计算了TRISO颗粒热导率，研究了各层厚度对TRISO颗粒等效热导率的影响.随后，构建了FCM核燃料芯块等效代表性体积单元，将多层TRISO球状颗粒热学性能等效为FCM燃料芯块中的球体，直接进行两相复合材料热导率计算，并研究了TRISO颗粒分布对等效热导率的影响.并利用跨尺度等效方法解决了FCM芯块复杂微结构建模问题，降低了模拟难度.

1 有限元模型

1.1 TRISO颗粒多层球体模型

根据TRISO颗粒SEM的微结构特征建立有限元模型[13].TRISO颗粒为典型球体，是一种由五层包覆层构成的复合材料，这五层包覆层从内到外依次是：核心燃料UO2层、具有疏松结构的缓冲碳层 Buffer层、具有致密结构的IPyC层、SiC层以及OPyC层，且每一层材料的厚度并不完全相同.基于TRISO颗粒球体对称性，将TRISO颗粒的球体模型进行对称处理，简化之后的1/8模型如图1[13]所示.

图1 TRISO颗粒典型微结构及简化模型Fig.1 Typical microstructure and simplified model of a TRISO particle

1.2 FCM芯块跨尺度等效模型

基于扫描电镜图像对FCM芯块的微结构进行有限元建模[13]，其代表性体积单元如图2[13]所示.在代表性体积单元中白色区域为SiC基体，蓝色区域为TRISO颗粒.为了使代表性体积单元具有充分的FCM芯块微结构信息，使用随机吸附算法生成了多种不同规模的代表性体积单元[14]，并将其中的TRISO颗粒多层结构等效为实体球状颗粒.

图2 FCM芯块典型微结构及代表性体积单元Fig.2 Typical microstructure and representative volume element of a FCM pellet

FCM芯块代表性体积单元中实体TRISO颗粒随机分布且具有周期性几何特征.进行有限元计算时，对TRISO颗粒简化模型及FCM芯块代表性体积单元均划分了精细的4节点线性传热单元网格，因此文中对网格精度造成的影响不再进行讨论.

2 材料参数

在有限元模拟时采用未经辐射的UO2材料参数，其热导率随着温度升高而降低，在高温时其热导率的变化会趋于平缓.对于SiC基体及SiC层，均采用NITE-SiC材料参数，其热导率随着温度升高而显著降低，在高温下其热导率同样会趋于平缓[15].对于Buffer层及IPyC/OPyC层，由于其厚度及热导率均相对较小，温度对其热导率的影响可忽略不计，因此模拟中保持恒定[16].表1给出了SiC基体及TRISO颗粒各层在200 ℃时的热导率，其他温度下材料参数参照文献[15].

表1 SiC基体及TRISO 颗粒各层热导率

3 计算方法

3.1 TRISO颗粒热导率计算

利用有限元方法实现球体法对TRISO颗粒热导率进行计算.该方法符合TRISO颗粒服役时内部径向热流实际情况.在简化模型中TRISO颗粒被设定为多层球体，并在球体中心构建半径为r1的空心内球体，在球壁上施加较高温度作为热传导过程的热源；在简化模型的最外侧表面，即外球壁施加低温，形成温度梯度实现稳态热传导.如图3所示，r1和r2分别为内球壁和外球壁的半径，t1和t2分别为在内球壁和外球壁施加的温度.球体法计算TRISO颗粒热导率公式为

图3 球体法示意图Fig.3 Schematic illustration of the sphere method

(1)

式中：Q为流过内外球壁的热量；r1、r2分别为球壁导热模型中内外球壁的半径；Δt为内外球壁的温差.

3.2 FCM芯块等效热导率计算

根据FCM燃料芯块微结构特征，利用代表性体积单元方法构建具有周期性几何特征的有限元模型；将其中的TRISO颗粒多层结构等效为实体球状颗粒；并以3.1节中方法获得的TRISO颗粒等效热导率作为实体TRISO颗粒的等效热导率.对代表性体积单元施加温度梯度为200 ℃的周期性边界条件进行传热计算，这符合实际测试FCM热导率的工况条件.根据傅里叶定律，利用体积平均方法，计算各单元温度梯度的平均值和各单元平均热流密度的平均值，进而计算FCM燃料芯块热的等效热导率，公式如下：

(2)

4 TRISO颗粒热导率模拟计算与调控

4.1 温度影响及与理论计算对比验证

在对TRISO颗粒等效热导率进行有限元计算时，内芯UO2厚度为350 μm，Buffer层的厚度为70 μm，SiC层、IPyC层与OPyC层的厚度均为35 μm.图4中红色曲线为有限元实现球体法的模拟计算结果.可以看到随着温度升高，TRISO颗粒热导率不断下降，并在最后趋于平缓.温度为200 ℃时，TRISO颗粒热导率为6.13 W·m-1·℃-1，在温度为1 000 ℃时，TRISO颗粒的热导率下降为2.85 W·m-1·℃-1.温度升高导致FCM芯块热导率显著下降的原因主要是由于占比较大的UO2材料和热导率远高于其他各层的SiC材料的热导率均随着温度升高而下降[15].

图4 TRISO颗粒等效热导率Fig.4 Effective thermal conductivity of the TRISO particle

随后利用理论串联热阻公式对上述结果进行验证.根据欧姆定律可以知道电流与电阻之间存在反比关系，在稳态热传导过程中，可以将推动力温度差和热流之间的关系表示为[17]

(3)

式中：Q为热量；Δt为温差；R为热阻.

对于层状复合材料而言，其总热阻是各层材料热阻之和，相当于多个具有不同热阻的材料进行串联，如图4中插图所示.因此TRISO颗粒的总热阻为

(4)

式中：λ为材料的热导率，下标表示TRISO颗粒不同包覆层；ri为每层包覆层的半径，下标代表TRISO颗粒的不同包覆层.其中rinner为球体模型中的r1,rOPyC为球体模型中的r2.

结合公式(1)则得到TRISO颗粒热导率的理论计算公式：

(5)

式中：λT为TRISO颗粒的热导率.

图4中蓝色曲线为理论计算的TRISO颗粒热导率曲线.可以看到TRISO颗粒的有限元计算热导率与理论热导率的变化趋势完全相同，且差异较小，证明了所采用模拟方法的有效性.

4.2 TRISO颗粒结构调控

调控TRISO颗粒结构层从而改善其性能一直是高性能FCM芯块设计的重点.在200 ℃下对TRISO颗粒各包覆层的厚度对其热导率的影响进行参数化研究.对TRISO颗粒的各包覆层厚度分别进行调控时，只改变被调控层的厚度，保持其他层厚度不变.

如图5a所示，UO2层厚度变化会对TRISO颗粒的热导率产生显著影响.随着UO2层厚度增加，TRISO颗粒的热导率显著增加；图5b中Buffer层厚度与TRISO颗粒热导率成反比，可见Buffer层厚度增加，TRISO颗粒的热导率反而减小.这可归因于Buffer层自身极低的热导率.图5c IpyC/OpyC层的厚度变化并不会显著影响TRISO颗粒的热导率.这是因为IpyC/OpyC层的热导率和初始厚度均较小导致的.由图5d可以看到SiC层的厚度变化也会对TRISO颗粒的热导率产生一定影响.虽然SiC层的初始厚度较小，但其热导率远高于其他层，因此增加该层的厚度可一定程度改善TRISO颗粒整体热导率.

图5 TRISO颗粒各层厚度对其等效热导率的影响

总体而言,增加UO2层、SiC层厚度可进一步改善TRISO颗粒热导率，而增加Buffer层厚度将不利于改善TRISO颗粒导热性能.调控IpyC/OpyC层厚度对TRISO颗粒热导率影响不大.考虑UO2层本身为核心燃料，同时SiC层厚度过大，其最大环向压应力会降低[18].因此，在满足TRISO颗粒尺寸及燃料含量要求的前提下可适当调控SiC层厚度以改善TRISO颗粒热导率.

5 FCM芯块等效热导率模拟计算与结构设计

5.1 收敛性验证及与实验结果对比

利用有限元方法进行复合材料性能研究时，代表性体积单元方法是常用方法，其模型规模的选取至关重要[19].因此首先对代表性体积单元规模进行研究.代表性体积单元立方体尺寸为L，TRISO颗粒直径为d.R=L/d为代表性体积单元的规模.模拟计算时TRISO颗粒为实体块状球体，通过调控L及TRISO颗粒数量来改变R大小并使TRISO颗粒体积分数保持20%恒定.TRISO颗粒热导率采用第4节中有限元计算得到的TRISO颗粒的等效热导率.计算得到的对比结果如图6所示.

图6 FCM代表性体积单元规模收敛性验证Fig.6 Verification of scale convergence of RVEs of FCM pellets

从图6可以看到，R从2增加到10时，FCM芯块的热导率逐渐增大然后趋于平稳.针对不同尺寸模型，建立了5个随机模型并对模型之间的误差进行统计.从图中可以看出，随着R增加，随机模型的计算结果差异逐渐减小.在R超过6以后，模拟结果已经趋于稳定.因此可以认为R≥6的代表性体积单元中已经包含了足够的FCM芯块的微结构信息，能够准确地对FCM芯块的热导率进行有效模拟.基于准确性与计算成本权衡的考量，后续计算的随机模型均选择R=6的代表性体积单元对FCM芯块的热导率进行研究.

随后对TRISO颗粒体积分数为37%的FCM芯块的热导率进行计算，并将模拟结果与实验中测得的热导率进行对比[15]，结果如图7所示.可以看出，计算得到的FCM芯块的热导率变化趋势与实验结果一致,当TRISO颗粒含量为37%时，模拟热导率为51.9 W·m-1·℃-1，与实验中测得的47 W·m-1·℃-1较为接近.模拟结果稍高于实验结果的原因是等效处理时忽略了各层之间热导率的差异.可以认为利用跨尺度模拟方法对FCM芯块的热导率进行模拟计算是高效且合理的.

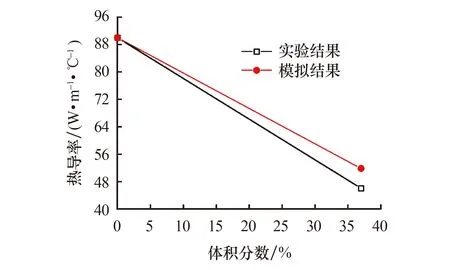
图7 模拟结果与实验结果对比Fig.7 Comparison of the experimental and simulated results

5.2 温度及TRISO含量对FCM芯块热导率的影响

图8为含不同体积分数TRISO颗粒的FCM芯块热导率随温度的变化情况.可以看出，在同一温度下，TRISO颗粒体积分数从10%增加到40%时，FCM芯块的热导率直线下降.这是由于在同一温度下TRISO颗粒的热导率远小于SiC基体的热导率，因此TRISO颗粒的体积分数越大，FCM芯块中SiC基体的体积分数就越小，芯块整体的热导率也就越小.在相同体积分数、不同温度时，FCM芯块的热导率逐渐减小最后趋于平缓，尤其在高体积分数下这种下降趋势会越来越缓慢，这是由于FCM芯块中的SiC基体和TRISO颗粒的热导率均随着温度升高而降低，且在高温阶段趋于平缓所导致.

图8 TRISO含量对FCM芯块等效热导率的影响

5.3 FCM芯块微结构设计

受材料科学中原子在晶体中的排布方式启发，设计了TRISO颗粒在FCM芯块中的三种不同有序排布方式，分别为FCM芯块的简单立方结构(SC结构)，体心立方结构(BCC结构)和面心立方结构(FCC结构).设计的TRISO颗粒在FCM芯块中的不同排布方式如图9a所示.通过改变代表性体积单元的立方体尺寸L调控不同排布方式下TRISO颗粒的体积分数.

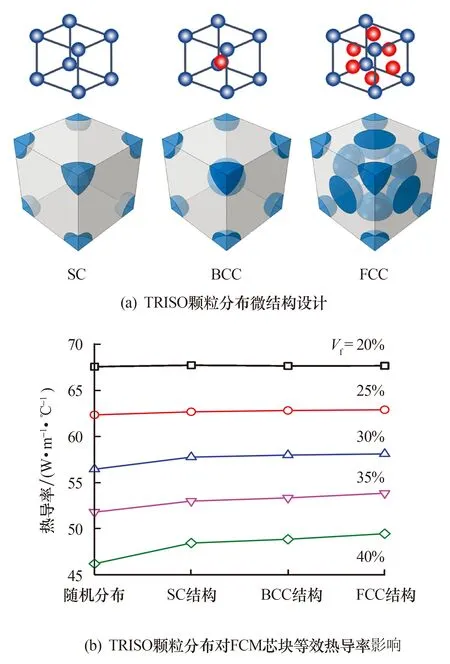
图9 FCM芯块微结构设计及其等效热导率Fig.9 Engineered microstructures of FCM pellets and their thermal conductivities

由图9b中可以看到，在TRISO颗粒体积分数较低时，几种TRISO颗粒的FCM芯块热导率几乎保持一致.随着TRISO颗粒体积分数逐渐增加，有序结构的热导率会逐渐增大，当TRISO颗粒体积分数为40%时，随机结构的FCM芯块热导率最低.这可归因于热传导过程中热流会优先流向热导率高的通道，随机结构中低热导率的TRISO颗粒随机分布导致热流被阻断.

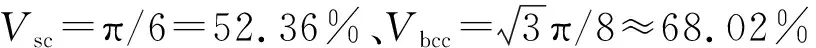
6 结论

利用有限元模拟对TRISO颗粒及FCM芯块等效热导率进行了模拟计算及结构设计，得出如下结论：

1) 有限元模拟实现球体法可以有效计算TRISO颗粒等效热导率.UO2层及Buffer层厚度对TRISO颗粒热导率有显著影响，两者厚度与TRISO热导率分别为正比与反比关系；IpyC/OpyC层的厚度变化对TRISO颗粒热导率影响不大；可通过调控SiC层厚度进一步改善TRISO颗粒热导率.

2) 采用跨尺度代表性体积单元对FCM芯块等效热导率进行计算，其模型规模R大于6时计算结果收敛.服役温度升高及TRISO含量增加，均使得FCM芯块等效热导率显著下降，但随着TRISO含量增加，温度对FCM芯块等效热导率影响减弱.

3) FCM燃料芯块中TRISO颗粒呈FCC结构分布时,其填充量可达74%.模拟结果表明，相比随机分布、SC结构分布、BCC结构分布，TRISO颗粒呈FCC状分布时，FCM燃料芯块具有更好的导热性能.

致谢：本文得到光合组织光合基金(202202012021)的资助，在此表示感谢.