涡轮导叶位置对封严效率预测模型的影响

杜林茂, 赵国昌

(中国民航大学 适航学院, 天津 300300)

随着现代航空工业的发展,航空发动机的设计者们追求更高的涡轮前温度,以获得更大的推力.因此，需要压气机提供更多的冷气对热端部件进行封严和冷却.在涡轮中,由于主流通道和动静盘腔之间存在压力差,所以外环主流燃气有入侵到盘腔的趋势.有研究表明[1]：入侵涡轮盘腔的燃气浓度增加1%,就会降低涡轮盘50%的寿命；如果使用的封严冷气量降低50%,涡轮效率将升高0.5%.因此,利用较低的封严冷气使用量达到更好的封严和冷却效果是设计者们追求的目标.

在燃气涡轮中,因导叶的存在,使得气流流过导叶时,在叶栅通道内和叶片下游会形成周向非均匀压力场.导叶的位势作用会同时对前排和后排动叶产生非定常影响.位势作用产生的周向非均匀压力场是燃气入侵发生的主要因素,由这一因素引发的燃气入侵被称为外环诱导燃气入侵(Externally Induced Ingress).Korakianitis[2]通过数值方法研究了上游静子尾迹对下游转子的非定常作用,结果显示当静子与转子的叶片数之比R>3时,导叶的位势场对转子的非定常作用占主导地位.Roy等[3]通过实验研究了2种不同动静叶设置下的燃气入侵,在实验中测量了不同位置的压力周向分布,结果表明周向压力差随着和静叶尾缘距离的增加而递减,但是周向压力最大值出现的位置却不随该距离的增加而改变.

在研究燃气入侵问题时,研究者普遍使用封严效率来评判涡轮盘燃气入侵的程度和冷却封严的效果.在理论研究和数值计算中,可以使用以质量流量定义的封严效率[4]，而用封严间隙处的出流气(Egress)和入流气(Ingress)的质量流量以及封严气体的质量流量即可计算封严效率.由于在实验中无法分别准确测得入侵燃气的质量流量,Graber[5]在封严气中加入二氧化碳气体作为示踪气,所以适合实验研究使用的是利用浓度定义的封严效率，即用测量点、主流入口处、封严气入口处的示踪气体浓度便可计算封严效率，并称为浓度效率.

关于燃气入侵封严效率的计算和预测,Pardeshi等[6]提出了降阶预测模型,模型将难以测量的质量流量之比降阶简化为盘腔尺寸之比,输入转子转速、主流和封严流质量流量以及封严结构和盘腔的尺寸即可大致估算出封严效率.Bayley和Owen[7]通过旋转盘腔实验,提出旋转诱导的燃气入侵主要与转子转速和封严间隙的大小有关.贾惟[8]提出封严腔几何结构会对涡轮性能产生影响,会使轴向封严气动性能更好,而径向封严的封严效率更高.降阶预测模型的思想与以上结论有一定重合度.

将某一工况下降阶模型的预测结果与英国巴斯大学的实验数据[9]对比,封严效率的预测结果最大相对误差为5%～15%,最小封严效率的预测相对误差达到了30%.模型存在一定的优化空间.

研究导叶位置以及外环压力场的形成和变化规律是从燃气入侵问题的发生机理入手,这对于研究和控制燃气入侵有着重要意义.本文将通过数值模拟的方法,研究导叶与封严结构的相对位置对外环压力场和燃气入侵的影响,并利用数值计算结果对预测封严效率的降阶模型进行优化.

1 模型建立和数值方法

1.1 降阶预测模型

对于燃气入侵过程,外环主流燃气在周向不均匀压力场和动盘的旋转作用下,由宽度为h的封严间隙入侵到盘腔内,如图1所示.盘腔外径为Rout,内径为Rin,封严间隙内的流动情况与周向压力梯度有关.

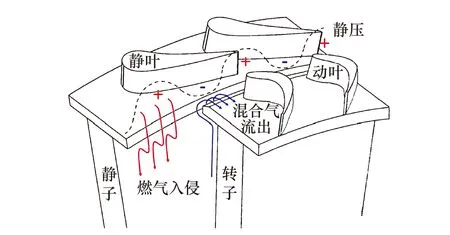
图1 外环周向非均匀压力场Fig.1 Circumferential non-uniform pressure field in annulus

降阶模型定义了大小介于Rout和Rin之间的参数临界半径Rcr以及常数C=Rin/Rcr.对于燃气入侵问题,存在两阶段.第一阶段当常数C1=Rin/Rout为常数时,无燃气入侵发生,因为在此时给定的主流流量、盘腔结构、封严结构、转子转速、导叶位置的条件下,封严流已经达到了足够的流量来防止入侵；第二阶段,燃气出现入侵,C2从定值Rin/Rout开始变化,当燃气入侵刚刚开始发生时,所用的封严流量即为该工况下的最小封严流量.对于给定的盘腔和封严结构,任何封严流量的减少、外环压力场的增大以及转子转速的增加都会使得入侵燃气增加.Rcr的定义与入侵盘腔的体积分数有关,封严效率与Rcr的关系推导如下：

利用质量流量定义的质量效率为

(1)

假设入侵盘腔的气体和封严气体为不可压的并且密度相同,那么由质量流量定义的质量效率可简化为由封严流体积流量Q和入侵体积流量Qi定义，即

(2)

由于体积流量比和体积比相等,所以式(2)可以利用盘腔部分体积Vpartial和盘腔整体体积Vfull之比表达，即

(3)

继而可以推出Rcr的表达式为

(4)

根据文献[6]给出的模型,在燃气入侵发生时，

(5)

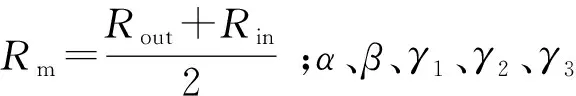
气体所有热力学特性和湍流输运特性都是在静子上游燃气的静温下评估的.由于外环燃气平均流速Va与转子转速ω呈线性关系,所以对于一个给定尺寸的实验台,外环雷诺数Rea=f(Va),Reω=f(ω),Rea=C·Reω.本文参考英国巴斯大学1.0级涡轮实验台,基于此实验台结构,C=0.538[6],因此,

Rea=0.538·Reω

(6)

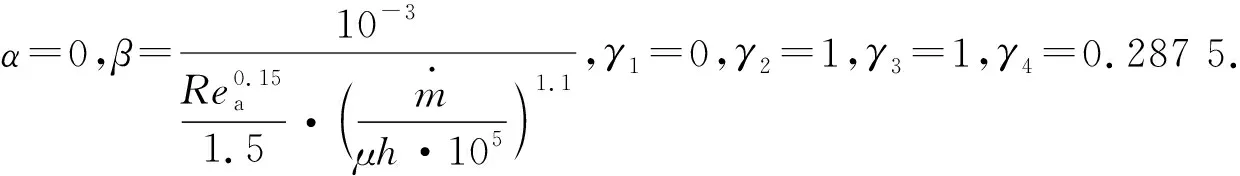
(7)

1.2 数值计算模型

以英国巴斯大学1.0级涡轮实验台为研究对象,该涡轮实验台横截面如图2所示[9],实验台具体的几何参数可参见文献[9] . 由于本文主要研究目标是探究不同导叶位置下的模型优化问题,所以出于简化模型、加快计算速度、节约计算资源的考虑,模型中只保留盘腔和带导叶的主流通道,略去了转子叶片，封严结构也选取了简单轴向封严.

图2 BATH1.0级涡轮横截面示意图

1.3 数值计算方法

由于计算模型中不含动叶,故将计算域整体设置为静止域,仅将动盘壁面设定为转动壁面.

数值计算使用FLUENT软件,由于流场中流动会在静叶处和封严结构处发生多处分离,在盘腔内部和封严通道内会产生旋流,所以在数值计算中选择标准k-ε湍流模型,求解三维定常雷诺平均N-S方程.计算网格290万,盘腔封严结构处网格与主流通道网格完全匹配,如图3所示.壁面第一层网格高度为0.003 mm,确保y+值小于2,静叶区网格划分如图4所示.主流和封严流进口均为质量流量边界条件,流动方向垂直于边界,出口设置为静压边界条件,静止壁面均为绝热、光滑、无滑移壁面.主要工质为理想空气,在主流中加入5%质量分数的二氧化碳作为示踪气体,后期通过盘腔内部示踪气体浓度计算封严效率.

图3 封严处与主流匹配的网格Fig.3 Matched grid at rim seal

图4 静叶区网格Fig.4 Grid at vane

数值计算中选取的转子转速为314 rad/s,主流进口质量流量为0.51 kg/s,封严流质量流量为0.006～0.07 kg/s.

2 计算结果和分析

2.1 验证计算

本文以英国巴斯大学已发表的实验数据和本文得到的数值仿真计算结果为基础,对降阶模型进行优化.通过验证计算,来证明数值仿真结果可靠.

图5给出了图2所示封严结构在314 rad/s的转速下,数值计算结果和实验数据的对比分析,取静盘表面径向位置R=r/b=0.958[10]处的封严效率数据.可以看出，数值仿真计算结果与实验结果较为吻合.在低封严流量和最小封严流量时的结果非常接近;在中等封严流量处的误差较大;最大相对误差约为-6.8%,在可接受范围内.由此证明，本文选择的数值模拟方法可以较为真实可靠地对燃气入侵物理过程进行仿真.

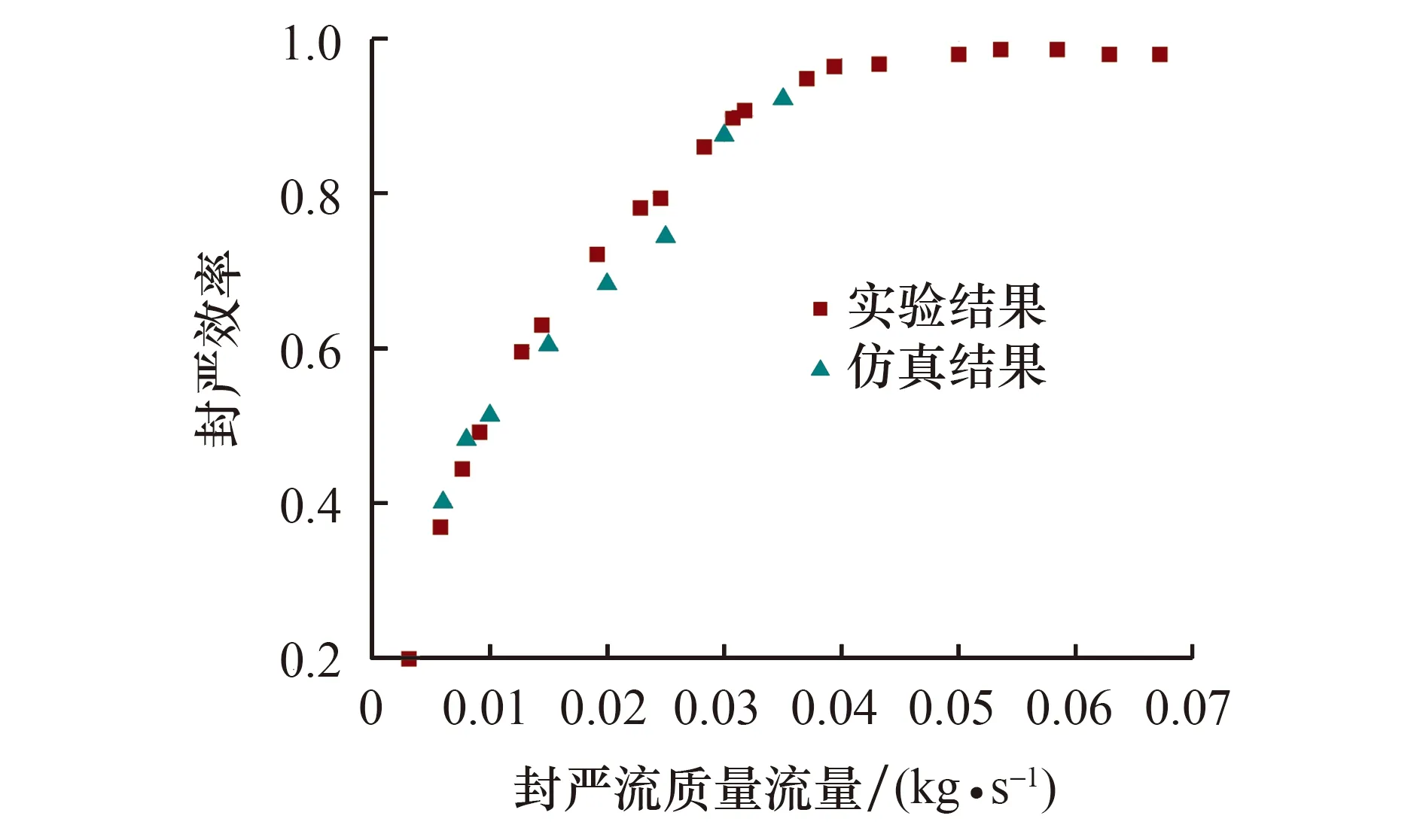
图5 封严效率验证计算结果Fig.5 Verification results of efficiency

为确保数值计算结果与网格数量无关,将原计算网格(290万)分别加密到高密度网格(435万)和减少到低密度网格(193万),分别进行计算.转子转速为314 rad/s,封严结构为轴向封严,封严冷却流量为0.03 kg/s,选取静盘表面浓度效率的径向分布情况作为考察对象,结果如图6所示.

图6 不同数量网格下的静盘表面效率分布Fig.6 Surface efficiency of stator with different number of grids

可以看出，低密度网格下得到的封严效率结果与其他网格相比略微偏低,而高密度网格和计算网格的结果几乎相同.因此可以说明数值计算的结果几乎不受网格数量的影响.下文的计算均使用中等密度网格,网格数量约为290万.

2.2 数值模拟计算

以验证计算模型为基础,分别将导叶的位置沿轴向靠近或远离封严结构移动2 mm,如图7所示.将导叶尾缘到封严结构的相对位置记为Δx,则Δx1=5 mm，Δx2=3 mm，Δx3=7 mm.计算设置和边界条件与2.1节验证计算完全一致.

图7 3种不同导叶位置Fig.7 Three guide vane positions

2.3 计算结果分析与讨论

图8给出了在3种导叶位置下盘腔封严效率随封严流量变化曲线图.可以看出，导叶位置的改变对封严效率有一定的影响,大约使封严效率在1%～4%波动.在封严流量较小和接近完全封严时,3组数据几乎重合;在中等封严流量时,出现了较为明显的差异,距离封严结构更近的P2位置导叶使得封严效率降低,距离封严结构较远的P3位置导叶使得封严效率提高.由此可以证明导叶位置对燃气入侵起到一定的支配作用.

图8 3种导叶位置下的封严效率Fig.8 Sealing efficiency under three guide vane positions

图9给出了封严间隙位置的外环静压云图.可以看出：P2位置的高压区和低压区面积均大于P1和P3位置,高压区域范围较大对燃气入侵较为不利；在周向位置中部,即导叶尾缘区域,P2位置的压力梯度较小,P1和P3位置的静压变化较为剧烈.

图9 3种导叶位置下的外环静压云图Fig.9 The static pressure contour of the annulus under three guide vane positions

图10给出了封严间隙涡轮盘半径R=203 mm处的静压折线图.可以看出，P1和P2位置的静压曲线几乎重合,导叶位置距离封严间隙最远的P3位置在负压力区和正压力区的压力绝对值基本都小于P1和P2位置,压力梯度较小.

图10 封严间隙R=203 mm处周向静压折线图 Fig.10 Circumferential static pressure at rim seal and R=203 mm

当导叶位于P2位置时,Pmax=2.72×105Pa,Pmin=-3.14×105Pa,可得最大压力差为

ΔP2=P2,max-P2,min=5.86×105Pa

同理计算可得P1和P2位置的最大压力差为

ΔP1=P1,max-P1,min=5.72×105Pa

ΔP3=P3,max-P3,min=5.26×105Pa

从3种静叶位置产生的周向压力分布来看,静叶后缘距离封严间隙的轴向距离越大,周向最大压力差越小,压力周向分布的不均匀性越弱.周向压力差越大,涡轮盘腔封严效率越低,达到同样封严效果需要的冷却流量越大.正负压最大值出现的位置没有发生变化,最大负压出现在周向0°,最大正压出现在周向11.25°.

虽然在实际涡轮设计过程中,导叶位置的选择要考虑很多的因素,例如流过静子的气动损失、涡轮整体的气动性能、动静干涉和振动问题等,不可能因为控制燃气入侵就将静叶调整到远离动静盘间隙的位置;但是对于理论研究,通过改变导叶位置控制外环压力场,可便于对燃气入侵的机理进行研究.在各个涡轮实验台中,导叶的位置不尽相同,故在导叶位置这一方面对降阶模型进行优化,同样有利于将模型发展到更广的适用范围,使其适用于更多的实验台.

3 模型优化

图11给出了3种导叶位置下的封严效率与P1位置的模型预测结果对比.在低封严流量和最小完全封严流量附近,模型预测结果显著偏高.

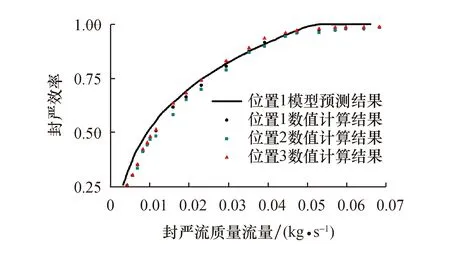
图11 模型预测结果Fig.11 Model prediction results

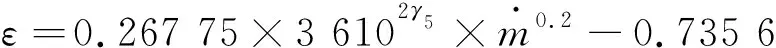
(8)

利用软件ORIGIN中的Simple Fit应用,对3组数值模拟结果进行曲线拟合.导叶位于P1位置时的结果如图12a所示,图中,A=2γ5,曲线拟合结果收敛性较好.当γ5=A/2=0.148 5时,降阶模型的预测结果与数值计算结果更为接近.

同理,其他2种导叶位置下的γ5最优解如图12b和图12c所示.

图12 导叶P1～P3位置拟合曲线Fig.12 Fitting curve of guide vane P1～P3 position

表1归纳了导叶尾缘到封严间隙的相对位置Δx与参数γ5拟合结果的对应关系.

表1 3种导叶位置的适用γ5值

将3组Δx和γ5的对应数据点进行线性回归拟合,结果如图13所示.Δx和γ5的关系式为

图13 Δx和γ5 线性拟合结果Fig.13 Linear fit results of Δx and γ5

γ5=0.147 54+1.975×10-4Δx

(9)

其中,Pearson相关系数为0.99 784,校正决定系数Adj.R-square为0.99.因此，可以认为Δx与γ5满足强烈的正相关线性关系.

4 结论

本文从燃气入侵的机理入手,探索导叶位置对外环压力场的影响；从导叶位置入手，优化预测封严效率的降阶模型；并且进行了数值模拟计算和回归分析.得到结论如下：

1) 改变导叶与封严间隙的轴向相对距离可以改变外环周向压力场,此压力场对燃气入侵起到支配性作用;叶尾缘与封严间隙的相对距离Δx越小,产生的周向压力梯度越大,外环压力场不均匀度增大,在相同工况下燃气入侵越严重,封严效率越低.

2) 不同导叶位置下,正负压最大值出现的位置没有发生变化,最大负压出现在周向0°,最大正压出现在周向11.25°.

3)降阶模型中控制外环雷诺数的参数γ5与导叶和封严间隙的相对距离Δx呈强烈的正相关线性关系.