一道三角不等式的探讨

安徽省岳西县汤池中学 (246620) 储文著 杨续亮

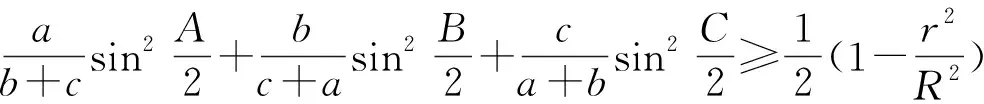
本文对不等式①，结合不等式②的形式结构提出一个类似不等式：

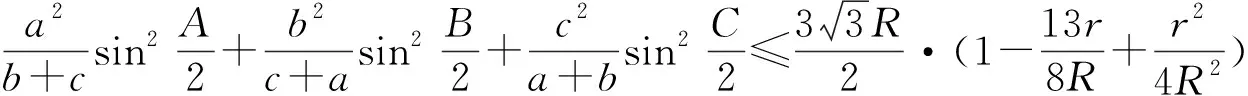
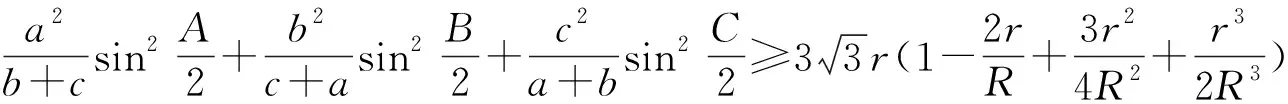
为了证明定理1，2先给出四个引理.

引理1[2]在△ABC中，有∑ab=s2+4Rr+

r2∑a2=2(s2-4Rr-r2)；∑a3=2s(s2-6Rr-3r2)；∑a4=2(s2-4Rr-r2)2-8s2r2.

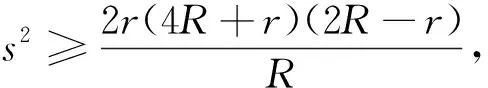
证明：由引理2和欧拉不等式R≥2r可知

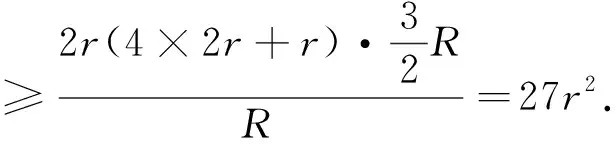
利用引理1和abc=4Rrs，可得:

(2s-a)(2s-b)(2s-c)=(a+b)(b+c)(c+a)=2abc+ab(a+b)+bc(b+c)+ca(c+a)

=2abc+ab(2s-c)+bc(2s-a)+ca(2s-b)

=2s(ab+bc+ca)-abc

=2s(s2+4Rr+r2)-4Rrs=2s(s2+2Rr+r2)；

∑a2(c+a)(a+b)=∑a2(2s-b)(2s-c)=∑a2[4s2-2s(2s-a)+bc)]

=∑a2(2sa+bc)=2s∑a3+abc∑a

=2s[2s(s2-6Rr-3r2)]+8Rrs2；

∑a3(c+a)(a+b)

=∑a3(2s-b)(2s-c)

=∑a3[4s2-2s(2s-a)+bc)]

=∑a3(2sa+bc)=2s∑a4+abc∑a2

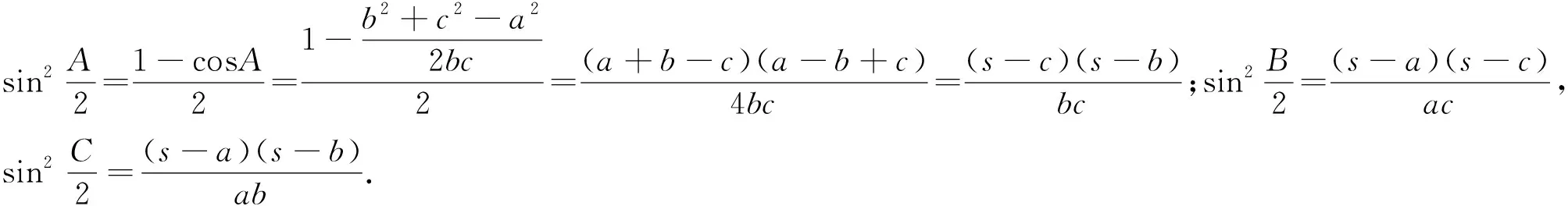
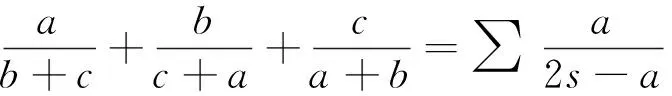
定理1的证明：根据熟知的欧拉不等式R≥2r可知 18R2-3Rr-2r2≥16R2+2R2-3Rr-2r2=16R2+(R-2r)(2R+r)≥16R2，于是有18R2-3Rr-2r2≥16R2⑤.⑤式等号成立当且仅当R=2r，即△ABC为正三角形时成立时.

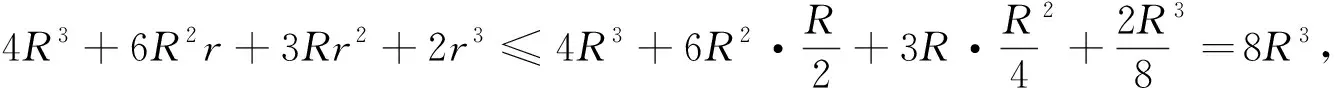
由引理3和引理4与⑥式等号成立的条件可知，不等式④等号当且仅当△ABC为正三角形时成立.