一种基于惯性测量单元和里程计的油气管道定位方法

闫雪娇,谢 哲,付宏文,蒋 松

（上海宇航系统工程研究所,上海 201108)

0 引言

随着城市化进程的加快,石油、天然气和饮用水的运输逐渐依赖于管道,管道在人们的生活中起到了越来越重要的作用[1-3]。近年来,多起管道泄漏爆炸事故为我们敲响了警钟,管道安全不仅关系到经济的发展,也与社会稳定息息相关,一旦油气管道发生事故,就会造成严重的生命和财产损失。

对管道进行定期检测可以提早发现管道故障并进行维修,这是避免管道事故的常见方法。管道定位作为管道检测中的重要一环,在管道安全运行中起到了重要的作用。国内外研究人员参考铁轨检测小车的形式,采用管道机器人进行管道检测。但因管道大多深埋地下,管道机器人搭载的检测设备无法接收到卫星导航信号,通常在管道机器人上加装惯性测量单元（Inertial Measurement Unit,IMU)和里程计等传感器构建导航系统,实现地下管道的定位和检测[4]。目前,常用的管道定位方法有纯惯性导航定位方法、视觉同步定位与映射方法和基于IMU/里程计组合定位方法等。由于纯惯性系统存在误差随时间累积的问题以及视觉同步定位方法存在长输气管道不适用性的缺陷,基于IMU和里程计的组合导航定位方法成为了主流。岳步江等[5]设计了一种IMU/里程计/地面标记器的组合定位方法,纪文涛等[6]使用Kalman滤波将IMU和里程计数据进行融合实现了管道的定位,Sahli等[7]提出了一种基于高精度三维简化惯性系统和里程计组合的管道定位方法,上述方法数据融合方式复杂,对传感器要求较高,且定位检测方法复杂。

本文从实际工程应用角度出发,针对油气管道定位问题,设计了一种基于IMU/轮式里程计的管道定位方法。该方法使用搭载在管道机器人上的IMU和里程计测量载体的运动信息,经离线解算获得管道机器人的运动轨迹。针对初始对准不准确造成的轨迹偏差,使用基于首尾点坐标的轨迹校正方法补偿初始条件带来的常值角度误差,得到准确的管道定位结果,使油气管道的定位成为可能。

1 管道定位系统概述

基于IMU的惯性导航系统自主性高,能获得较全面的导航信息,但存在累积误差的问题。在不发生相对摩擦的条件下,里程计可测量载体准确的速度信息。使用IMU解算的姿态信息和里程计的速度信息即可实现管道机器人行进轨迹解算,满足地下管道定位的需求[8]。管道定位系统原理图如图1所示,其由IMU、里程计和存储设备组成。在管道机器人进行测量作业时,将传感器的测量数据存入存储设备,待管道机器人走完全程后再对数据进行离线分析,完成整个管道定位过程。

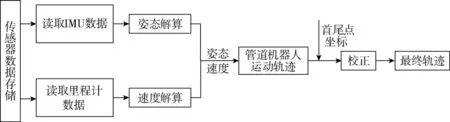
图1 管道定位系统原理图Fig.1 Schematic diagram of pipeline positioning system

测量工作完成后,从数据存储设备中读取IMU数据和里程计数据,解算IMU中的陀螺仪数据获得管道机器人的姿态信息,解算里程计数据获得速度信息。利用上述的姿态信息和速度信息计算管道机器人的相对位置,进而绘制出管道机器人的运动轨迹。由于初始对准阶段设定的初始值精度不高,此时的管道机器人运动轨迹与其真实轨迹之间存在一个常值角度偏差,本文采用基于首尾点坐标的轨迹校正方法对该角度偏差进行补偿,最终获得准确的管道定位信息。

2 基于IMU和里程计的管道定位方法

本文设计的管道定位方法是一种离线的数据处理方法,其算法流程如图2所示。

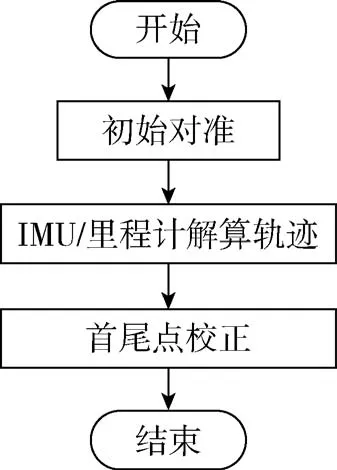
图2 定位算法流程图Fig.2 Flowchart of positioning algorithm

IMU和里程计完成管道数据采集后,首先对IMU进行初始对准,确定捷联矩阵的初始值。然后解算IMU陀螺仪数据,获得管道机器人姿态信息,结合轮式里程计解算的速度信息确定管道机器人的运动轨迹。最后,采用首尾点坐标校正方法补偿常值角度误差,实现油气管道的定位。

2.1 坐标系及姿态定义

本文涉及的坐标系定义如下,坐标系之间的关系如图3所示。

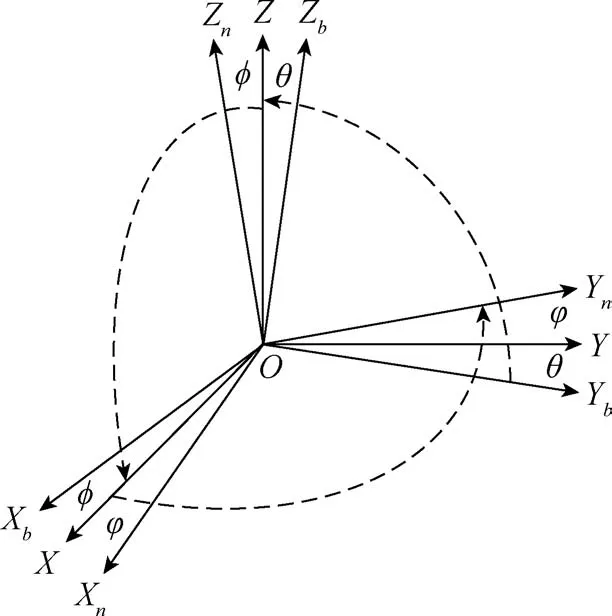
图3 坐标系关系图Fig.3 Relation diagram of each coordinate system

1)导航坐标系（n系,OnXnYnZn):即管道机器人相对地球位置的坐标系,是导航系统工作时选取的基准[9]。本文选取东北天坐标系作为导航坐标系,以管道机器人中心为原点,OnXn指向地球正东,OnYn指向地球正北,OnZn沿垂线方向指天向。

2)管道机器人坐标系（b系,ObXbYbZb):即固连在管道机器人上的坐标系。本文定义右前上坐标系为管道机器人坐标系,其坐标原点与导航坐标系重合,为管道机器人中心,ObXb沿管道机器人横轴指向右侧,ObYb沿管道机器人纵轴指向前方,ObZb由原点指向管道机器人上方。

导航坐标系和管道机器人坐标系不重合,两者之间的夹角恰好反映了管道机器人运动的姿态角[10]。本文规定管道机器人坐标系ObXbYbZb绕X轴旋转的角度为俯仰角,绕Y轴旋转的角度为横滚角,绕Z轴旋转的角度为航向角。将管道机器人坐标系按照一定顺序绕不同的坐标轴进行旋转后,两坐标轴即可重合,使两坐标轴重合的旋转顺序和角度组成的矩阵即为方向余弦矩阵Cnb。

2.2 IMU的初始对准

初始对准在惯性导航系统中尤为重要,只要给定导航的初始条件,便可根据IMU的数据解算出各种导航信息[11]。初始对准的任务是将载体的初始位置和初始速度引入惯性导航系统,建立初始方向余弦矩阵,使管道机器人坐标系与导航坐标系相重合。

初始对准在管道机器人测量初始时进行,此时管道机器人处于静止状态,载体的初始速度为零,初始位置为管道起始点坐标。由于管道机器人处于静止状态,所以其三个轴向的加速度向量之和等于重力加速度,可计算管道机器人的初始俯仰角和横滚角,求解公式如下

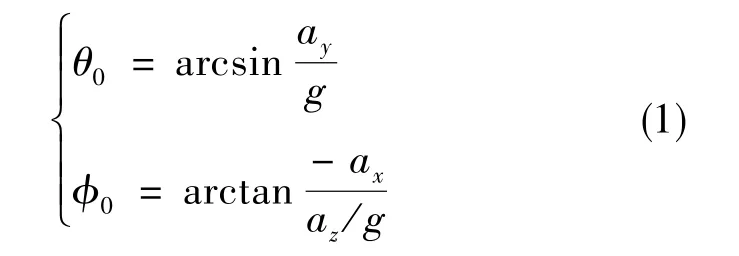
式（1)中,θ0为管道机器人的初始俯仰角,ϕ0为管道机器人的初始横滚角,ax、ay和az分别为管道机器人静止时加速度计三个轴向的测量值,g为当地的重力加速度（常值)。

管道机器人的初始方位角可根据管道首尾点坐标进行计算,计算公式如下

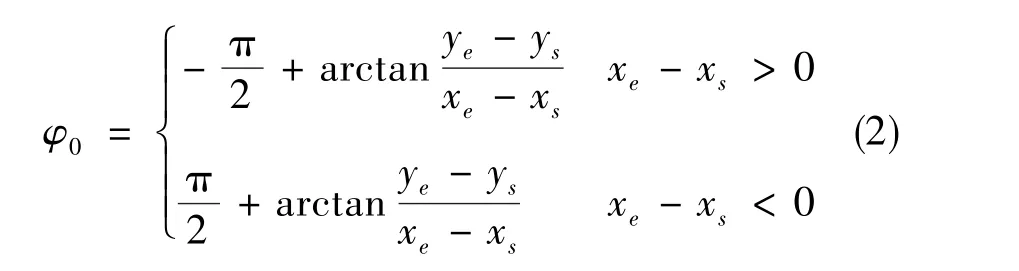
式（2)中,φ0为管道机器人的初始方位角,（xs,ys)和（xe,ye)分别为管道起始点和终止点位置坐标（x为东向坐标,y为北向坐标)。根据上文计算的初始姿态,可求出IMU的初始方向余弦矩阵,完成IMU的初始对准。

2.3 IMU/里程计的轨迹解算

惯性系统解算出的速度和位置信息具有误差随时间积累的缺点,为获得准确的管道机器人运动轨迹,本文结合IMU解算的姿态与里程计的速度求取管道机器人的位置信息,完成管道定位,轨迹解算原理图如图4所示。

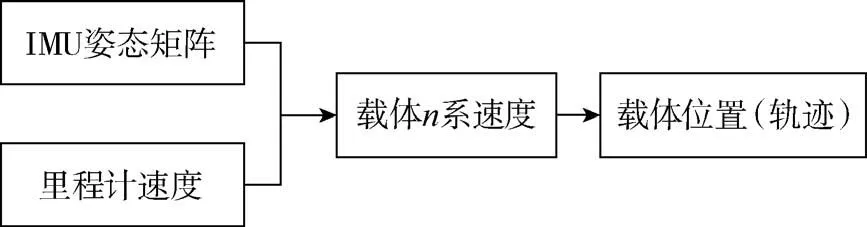
图4 轨迹解算原理Fig.4 Principle of trajectory calculation

（1)IMU姿态矩阵

IMU姿态矩阵即IMU的方向余弦矩阵,是b系到n系的坐标转换,常用来表示,计算方向余弦矩阵的常用方法有方向余弦法、Euler角法和四元数法。方向余弦法未知数数目较多,计算量较大;Euler角法求解存在奇点,不能对所有姿态进行求解,故采用计算量较小的四元数法进行姿态解算[12]。

四元数由1个实数单位和3个虚数单位组成,表示的是管道机器人坐标系到导航坐标系的转动,其表达形式如下

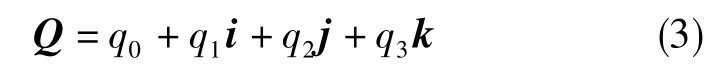
本文采用四阶Runge Kutta法求解四元数微分方程,根据IMU的陀螺仪数据实时更新四元数,计算出管道机器人的姿态矩阵,其计算公式如下

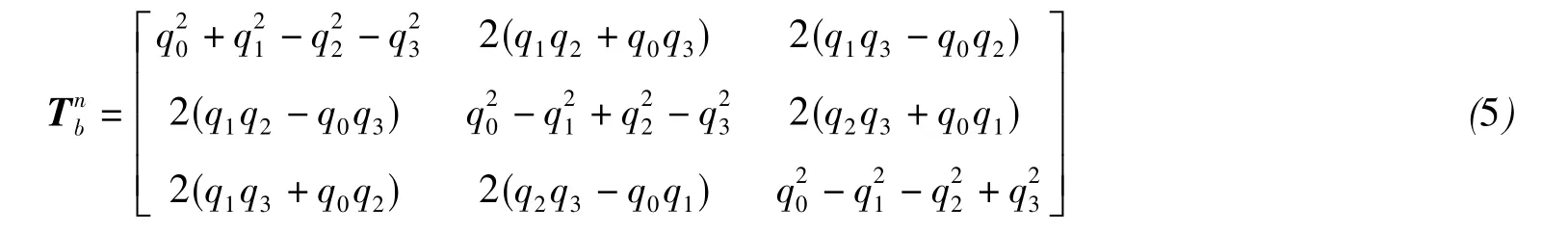
（2)里程计速度计算

轮式里程计是管道机器人搭载的常用传感器,可以测量载体的行进速度和路程[13-14]。为准确测量管道机器人的行进速度,减小在管道中里程轮发生打滑、飞转等情况带来的误差,本文在管道机器人后轮轮系搭载了两组轮式里程计测量载体速度,最终取左右两轮的平均速度作为管道机器人的b系速度。

本文采用的里程计采样频率为100Hz,轮盘每转动一周输出3个周期方波波形,根据相邻两点的数据差计算里程计测量的载体速度,其公式如下

式（6)中,vd为里程计测量的管道机器人速度,k为里程计刻度因数,d为里程计轮盘直径,Δn为里程计采集的相邻两点数据差,Δt为采样时间间隔。

里程计搭载在管道机器人的车轮上,测量的是管道机器人b系上的前向速度,故管道机器人的b系速度为

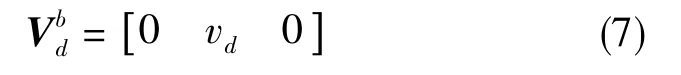
（3)轨迹解算

管道机器人的定位是在n系下进行的,需将里程计测量的b系速度转换到n系下,方可解算出管道机器人的运动轨迹。

获得管道机器人在导航坐标系下的速度后,将速度对时间进行累加,计算管道机器人的相对位置坐标,与管道起始点坐标相加后,得到管道机器人的绝对位置坐标,即为载体的运动轨迹。管道机器人的绝对位置计算公式如下

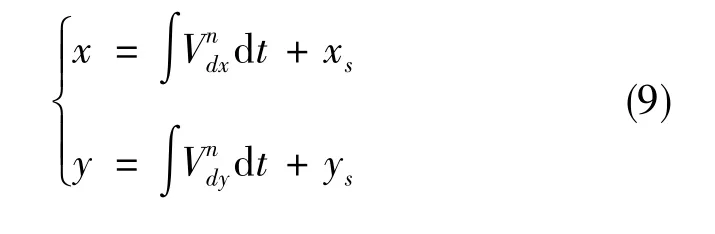
3 基于首尾基准点的管道定位校正方法

初始对准在IMU数据解算中尤为重要,设定准确的初始姿态矩阵,解算出的姿态信息才不会出现偏差。在上述管道定位算法中,由于初始对准阶段设定的姿态存在误差,导致解算出的每一点与管道起始点之间的连线以及该点的基准点与起始点之间的连线存在常值角度误差。针对这一问题,本文提出了基于首尾基准点的管道定位校正方法。

解算轨迹与实际轨迹之间的角度误差为常值,可根据解算出的始末点位置信息及其对应的基准点位置信息计算角度误差并在解算轨迹中进行补偿,以达到管道定位信息校正的目的。

以求解方位角常值误差为例,根据已知的被测管道基准始末点位置坐标,计算被测管道终止点相对于起始点的方向角,如式（10)所示。通过解算出的始末点位置坐标,计算解算的终止点相对于起始点的方向角,如式（11)所示。

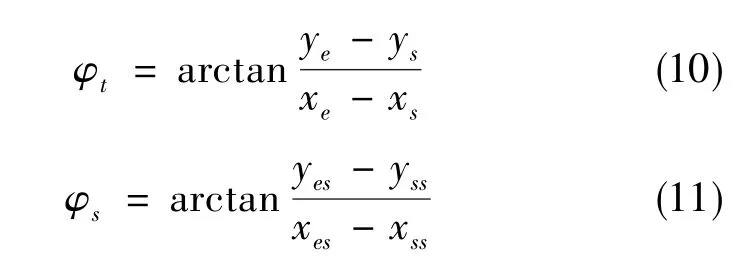
式（10)、 式（11)中, （xs,ys)和（xe,ye)分别为被测管道实际起始点和终止点的位置坐标,（xss,yss)和（xes,yes)分别为解算轨迹的起始点和终止点的位置坐标（x为东向坐标,y为北向坐标)。

最终,计算得到的方位角常值误差为

同理,可计算俯仰角和横滚角的常值误差Δθ和Δϕ。值得注意的是,管道机器人沿管道壁进行作业,工作时对横滚角影响较小,因此本文忽略了横滚角的常值误差。

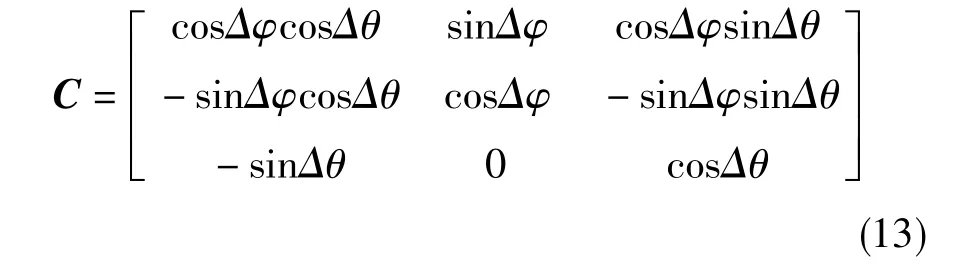
该旋转矩阵实现了解算轨迹的常值角度误差校正。

在实际应用中,由于里程计轮盘测量不准确等原因,里程计的刻度因数k会存在误差,影响管道机器人的定位精度。为获得准确的定位信息,需对里程计的刻度因数进行标定,本文采用基于首尾点坐标的方式来标定里程计的刻度因数。

里程计刻度因数k在数值上等于解算轨迹长度与实际轨迹长度的比值,本文根据解算的始末点位置和实际始末点位置标定里程计的刻度因数,标定公式如下

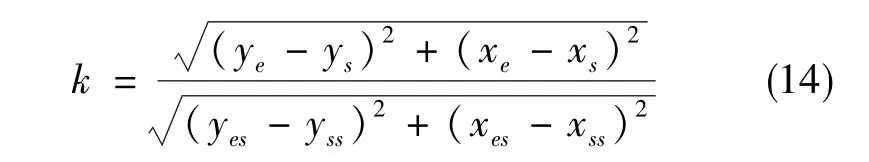
根据上文所述的旋转矩阵和里程计刻度因数校正解算的管道机器人行进轨迹,校正公式如下

式（15)中,X-为校正前的管道机器人行动轨迹,X为校正后的管道机器人行动轨迹。

4 管道定位测绘实验

为验证本文提出的轨迹校正方法的有效性,本文进行了管道定位测绘实验。为直观地显示本文方法的有效性,解算时分别绘制了校正前管道定位信息、校正后管道定位信息和被测管道的基准点位置信息,计算轨迹校正后本文方法的定位精度,验证本文方法的有效性和工程应用价值。

管道机器人由牵引装置拖拽在管道内做往复运动,管道机器人车轮直径为50mm,利用管道机器人搭载的IMU和里程计采集数据,实验时传感器的采样频率为100Hz。通过本文设计的管道定位算法解算管道机器人轨迹,得到管道的定位信息。管道机器人如图5所示,IMU和里程计分别搭载在管道机器人机身和后侧左右轮盘上。本文实验的定位基准为RTK测得的管道中心线数据,分别在两个场景中进行实验:一个是在果园里搭建的94m的S型管道,另一个是在农场地面铺设的900m管道。

图5 实验用轮式管道机器人Fig.5 Diagram of wheeled pipeline robot for experiment

4.1 94m管道定位实验

94m管道的实验场景如图6所示,其大致形状为 “S”形。利用管道机器人采集管道数据后,使用本文方法对采集的数据进行处理,分别绘制校正前、校正后的管道定位结果和管道中心线基准的俯视图和剖面图,如图7所示。

图6 94m管道实验场景Fig.6 Diagram of 94m pipeline experiment scenario

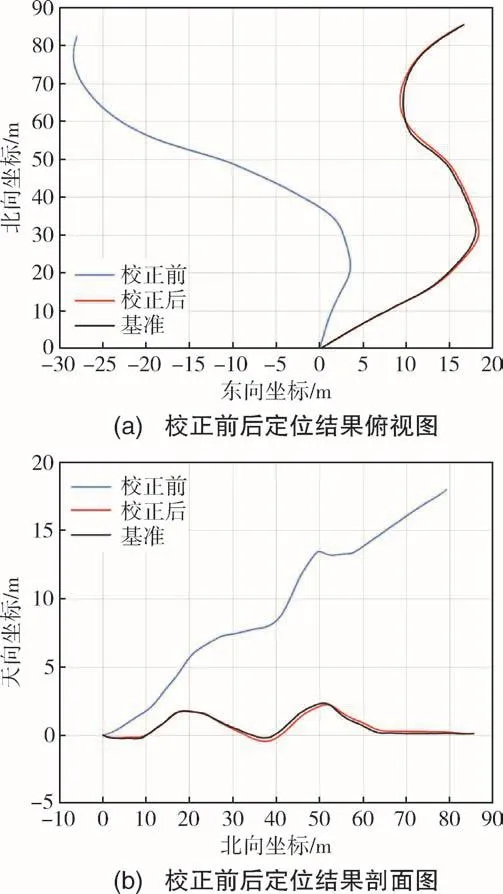
图7 校正前后的94m管道定位结果Fig.7 Positioning results of 94m pipeline before and after correction

由图7可知,校正前与校正后的管道机器人轨迹之间的角度误差为常值,校正前的管道定位结果与管道基准相差较大,校正后的管道定位结果与管道基准基本重合,说明了本文提出的管道定位校正方法的有效性。

为直观说明本文方法的有效性,现在管道中选取15个采样点,分别计算采样点上校正后的轨迹坐标与管道基准坐标之间的误差,统计水平定位误差和高程定位误差的最大值、均值和方差,计算结果如表1所示。

由表1可知,本文提出的管道定位校正方法能实现较为准确的定位。校正后的管道水平误差和高程误差的均值和方差均小于0.11%D,说明本文方法在管道定位数据解算中具有稳定性。同时,管道定位水平误差和高程误差分别为0.19m和0.09m,由定位精度等于定位误差与管道机器人航程之比可知,94m管道的水平定位精度为0.20%D,高程定位精度为0.10%D,该定位精度满足油气管 道测绘要求。

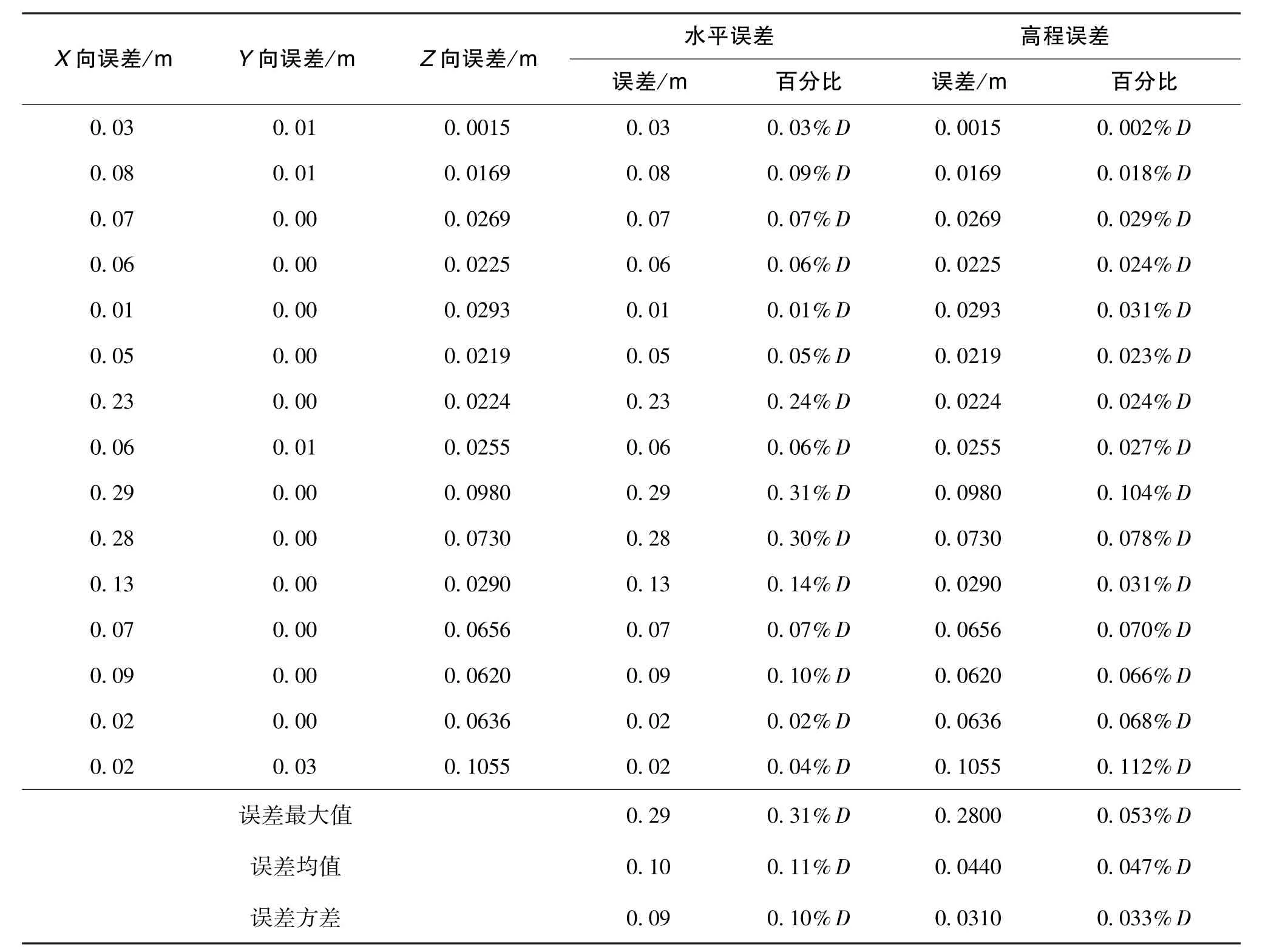
表1 校正后94m管道定位误差分析结果Table 1 Analysis results of 94m pipeline positioning error after correction

4.2 900m管道定位实验

900m管道的实验场景如图8所示,其形状为带有小幅度拐点的直线形。管道机器人采集管道数据后,使用本文方法处理数据,结果如图9所示。

图8 900m管道实验场景Fig.8 Diagram of 900m pipeline experiment scenario

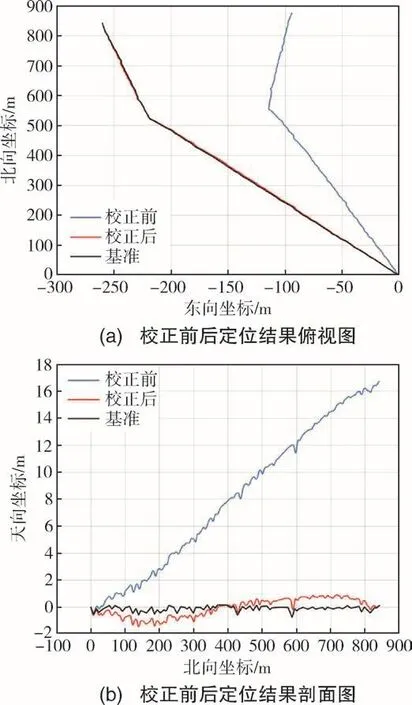
图9 校正前后的900m管道定位结果Fig.9 Positioning results of 900m pipeline before and after correction

与94m管道定位结果相同,校正前后900m管道定位结果之间的角度误差为常值,校正后的管道定位结果与管道基准基本重合,表明了本文提出的管道定位校正方法具有普遍适用性。

经计算,校正后900m管道定位结果的水平误差和高程误差如表2所示。由表2可知,校正后900m管道直线部分的水平定位误差为0.16%D,高程定位误差为0.10%D,弯道部分的最大水平定位误差为0.18%D,高程定位误差为0.10%D,且最大定位误差点出现在转弯或临近转弯处。

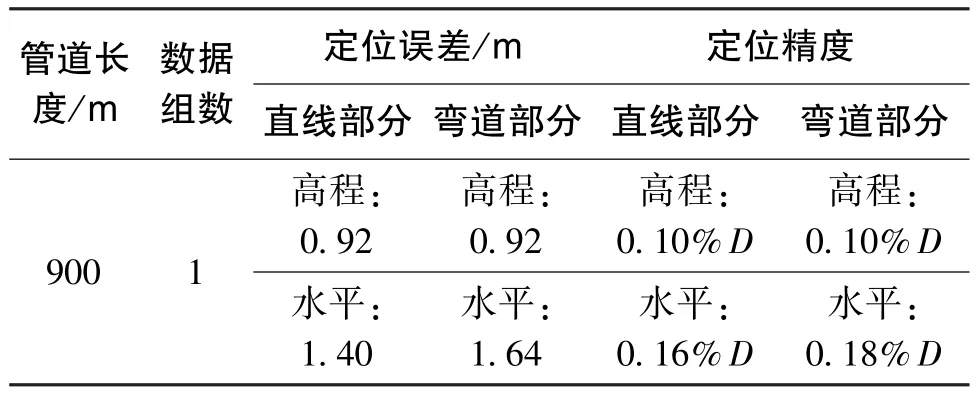
表2 校正后900m管道定位误差Table 2 Positioning error of 900m pipeline after correction

综上所述,本文设计的管道定位校正方法能有效补偿管道定位误差,该方法具有普遍适用性。该管道定位方法在油气管道定位中精度较高,尤其在直线形管道的定位中具有明显优势。当管道存在拐点时,拐点的幅度越小,其定位精度越高。但无论何种形状的管道,其水平定位精度均小于航程的0.20%,说明了本文方法在管道定位上的有效性。且常规管道多为直线型,相较于弯道数据解算,直线形管道数据的解算结果更有意义。

5 结论

本文设计了一种基于IMU和里程计的管道定位方法,通过解算IMU和里程计数据,实现了油气管道的定位。针对初始对准引入的常值角度误差,提出了基于首尾点坐标的轨迹校正方法,提高了管道的定位精度。采用管道测绘实验对本文方法进行验证,实验结果表明:本文提出的管道定位校正方法可有效补偿初始对准引入的角度常值误差,校正后的管道定位精度较高,且具有较好的定位稳定性。本文方法在管道定位中表现良好,水平定位误差和高程定位误差均小于航程的0.20%,可用于实际管道的定位测绘。在后续的管道定位中,将重点研究惯性导航转角、管道打滑等条件下的可靠定位问题。