基于遗传算法优化BP神经网络的半球谐振陀螺温度补偿

赵建宇,凌林本,冯毅博

（北京航天控制仪器研究所,北京 100039)

0 引言

半球谐振陀螺是一种新型的哥氏振动陀螺,与传统的机械陀螺相比,半球谐振陀螺没有高速旋转的转子,而是通过其核心部件——半球谐振子的径向振动产生驻波,再由驻波的进动敏感输入角速度。半球谐振陀螺具有体积小、质量小、寿命长、精度高、可靠性高以及抗辐射能力强等优点,尤其适用于工作环境恶劣、精度需求高并且长时间在轨运行的空间航天器上。半球谐振陀螺的漂移会严重影响其精度,文献[1]分析了由重力加速度、载体运动加速度引起的陀螺漂移并提出了基于动力学的加速度影响分析方法;文献[2]对由于谐振子质量不平衡、阻尼不均匀以及频率裂解等制造工艺的限制而引起的陀螺漂移进行了误差分析;文献[3]分析了由随机误差引起的陀螺漂移并采用了滤波技术进行估计与补偿。

温度的变化也是引起陀螺漂移的重要因素之一。半球谐振陀螺在工作时,环境温度的变化以及陀螺内部产热会影响谐振子的密度、半径、杨氏模量和泊松比等参数,使得谐振子的固有频率发生变化,陀螺的输出产生温度漂移。陀螺在输入角速度为零时的输出叫做零偏,零偏随温度产生的漂移严重制约了陀螺的精度,因此对零偏的温度漂移进行抑制或补偿是十分有必要的。许多科研人员在半球谐振陀螺的温度补偿方面都做出了贡献,文献[2]建立了半球谐振陀螺谐振频率与温度之间的对应关系,采用逐步线性回归法,基于谐振频率的变化完成了半球谐振陀螺的温度补偿;文献[4]对比了BP（Back Propagation)神经网络法和最小二乘法对半球谐振陀螺温度补偿的效果;文献[5]提出了一种改进PSO-ARMA（Particle Swarm Optimization-Autoregressive Moving Average Model)建模方法,对不确定性漂移进行了补偿;文献[6]利用回归理论对温度漂移数据进行分析,建立了半球谐振陀螺温度偏置漂移的多项式数学模型。

在实际应用中,由于半球谐振陀螺谐振子密封于真空罩内,难以直接获得其温度。因此,本文首先推导了谐振子温度与谐振频率的关系,然后建立了环境温度到谐振子温度的热传递模型,通过采集陀螺输出零偏随环境温度变化的数据信息,得到陀螺输出零偏随谐振子温度的变化关系,最后采用遗传算法优化BP神经网络的方法对陀螺温度漂移的数据进行补偿。该算法相较于最小二乘法的拟合精度更高,从而实现通过谐振频率对零偏温度漂移进行补偿的效果,提高了陀螺的使用精度。

1 半球谐振陀螺的温度特性

零偏会随温度的变化产生漂移,文献[7]指出,半球谐振子四波腹振动的谐振频率约为

式（1)中,h为半球谐振子的厚度,r为半球谐振子的中半径,E为杨氏模量,μ为谐振子材料的泊松比,ρ为谐振子材料的密度。上述变量中,受温度影响较大的为杨氏模量E,其随温度变化的关系为

式（2)中,E0为取常温时谐振子的杨氏模量;kE为杨氏模量随温度变化的系数,约为10-5量级。

将式（2)代入式（1)中,并进行Taylor展开得到

由于kE数值很小,因此可对上述展开式保留前两项,得到半球谐振子的谐振频率随温度变化的线性关系

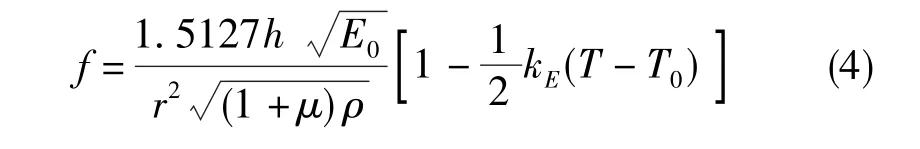
半球谐振陀螺的频率控制回路可以实时地获取谐振频率,因此通过式（4)可以实时地得到谐振子温度值。

2 半球谐振陀螺的温度建模

半球谐振陀螺在实际工作中难以直接获取谐振子温度值,因此可通过建立谐振子温度模型的方式间接获取。谐振子从环境吸热的过程是典型的热工过程,温度变化呈现有自平衡能力的特性,其传递函数可用一阶惯性环节近似表示[8]

式（5)中,K为放大系数,T为惯性时间常数,s为拉氏变换因子。对于参数K,可以采用两点法辨别得到

式（6)中,y（0)为初始输出值,y（∞ )为稳态输出值,Δx为控制输入量大小。

由于陀螺的输出零偏实时地反映了谐振子的温度值,因此可对陀螺输出曲线采用最小二乘法进行辨识,得到惯性时间常数T。

3 基于遗传算法优化BP神经网络的温度补偿

3.1 BP神经网络模型

BP神经网络是一种按照误差反向传播算法训练的多层前馈神经网络,它无需事先确定输入与输出之间的映射方程,而是仅通过自身的学习与训练,即可实现在给定某输入值时得到最接近期望输出值的结果[9]。BP神经网络的结构包含输入层、隐含层和输出层,其单隐含层网络结构如图1所示。

图1 单隐含层BP网络结构Fig.1 Structure of single hidden layer BP network

BP神经网络在使用时需要先用一组样本数据对网络模型进行训练,训练过程由信号的正向传播和误差的反向传播两部分组成[10]。正向传播过程为:样本由输入层进入网络,经过全部隐含层传至输出层,把输出层当前值与期望值进行比较,若误差值满足要求,则结束学习算法,否则进行误差反向传播的过程。反向传播过程为:误差按原通路反传计算,在反传过程中不断调整各层神经元的权值和阈值,以求正向传播的输出误差趋向最小。

BP神经网络可以很好地预测新输入的数据,具有强大的容错能力、非线性映射能力、自学习和自适应能力。但它容易陷入局部最优解,缺乏有效方法来选取非线性网络的学习速率,且初始权值与阈值的不确定会降低网络的训练能力,这些都制约了BP神经网络算法的性能。因此,需要考虑对该算法进行优化。

3.2 遗传算法优化BP神经网络

遗传算法是一种基于达尔文生物进化论和孟德尔遗传学说发展起来的可并行化处理和全局搜索的高效优化算法[11],它克服了传统算法容易陷入局部最优解的缺点,广泛应用于组合优化和自动控制等领域。遗传算法的基本运算过程为:编码、个体评价、选择、交叉和变异。编码是指用遗传空间的染色体或个体来表示要求解的问题,常用方法有二进制编码和实数编码等;个体评价是指通过适应度函数对每一个染色体进行度量,以区分出最优个体,淘汰最差个体;选择是以个体适应度为标准选择出最优秀的个体进行后续操作;交叉是模拟生物染色体交配重组,通过染色体的交叉产生新的个体;变异是模仿生物进化的基因突变,变异可以产生新的染色体,促进群体进化。像这样,新群体继承了上一代的信息,还优于上一代,反复循环,直到满足条件。

BP神经网络的初始权值和阈值通常采用[-0.5,0.5]之间的随机数,它对网络训练结果的影响很大又无法准确得到,因此引入遗传算法来优化出最佳的初始权值和阈值。优化算法采用遗传空间的个体代表网络的初始权值和阈值,将该个体值初始化BP神经网络产生的预测误差作为该个体的适应度值,然后进行选择、交叉和变异操作寻找最优个体,即最优的BP神经网络权值和阈值。遗传算法优化BP神经网络的流程图如图2所示。

图2 遗传算法优化BP神经网络流程图Fig.2 Flowchart of genetic algorithm optimizing BP neural networks

4 实验与结果

实验由两部分组成,实验一的数据用于辨识温度模型的参数,以得到谐振子温度随时间变化的关系;实验二的数据与实验一结果相结合,把环境温度与陀螺输出零偏的数据转换成谐振子温度与陀螺输出零偏的数据,从而用于遗传算法优化BP神经网络的训练与验证,具体实验操作如下:

（1)实验一

将半球谐振陀螺置于带有高低温箱的速率转台中,半球谐振陀螺及其控制电路板如图3所示。

图3 半球谐振陀螺及其控制电路板Fig.3 Diagram of hemispherical resonant gyroscope and its control circuit board

调整转台位置,使陀螺的输入轴平行于地理东西向,以保证陀螺的输入角速度为零。启动陀螺,常温下保持5h,待陀螺输出数据稳定后,将温箱温度以5℃/min速率由0℃升高至10℃,保持5h并记录陀螺输出,前100min的输出曲线如图4所示。

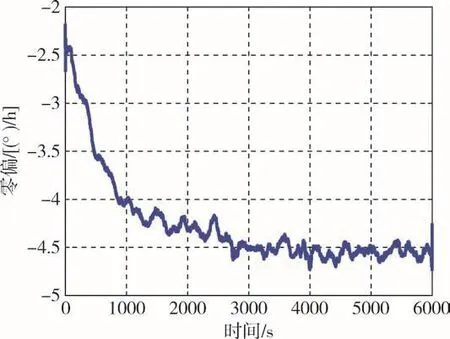
图4 陀螺对10℃温差的响应Fig.4 Diagram of gyroscope response to 10℃temperature difference

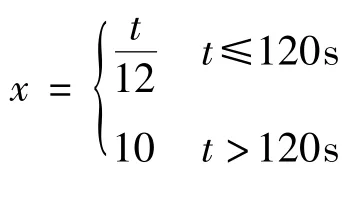
对图4曲线基于式（5)进行最小二乘拟合,得到当T=694s时拟合误差最小,误差的标准差约为0.0799（°)/h,得到的陀螺输出数据与拟合结果如图5所示。

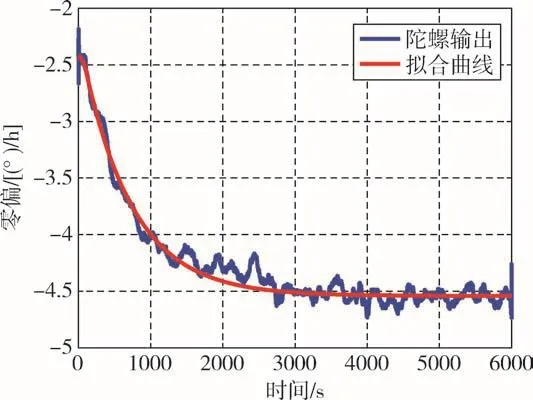
图5 陀螺输出与拟合曲线Fig.5 Diagram of gyroscope output and fitting curve

由图5可知,拟合效果较为理想,由此验证了提出的温度模型的有效性。

由上述温度模型参数辨识结果可知,谐振子温度响应的惯性时间常数为694s。因此可以得到,当环境温度从0℃以5℃/min速率升温至60℃时,环境温度变化与谐振子的温度响应如图6所示。

图6 环境温度变化与谐振子的温度响应Fig.6 Diagram of ambient temperature variation and temperature response of harmonic oscillator

为确保谐振子温度与环境温度达到平衡,环境温度在60℃应保持足够长的时间。由图6可知,环境温度在60℃保持了88min,足以使得谐振子温度达到稳态。由图6得到了谐振子温度随时间变化的关系,在环境温度相同变化的条件下,若得到谐振子输出零偏随时间变化的关系,即可得到谐振子输出零偏随谐振子温度变化的关系。

（2)实验二

在实验一的基础上,进行下述步骤:

步骤1:将温箱温度调整到0℃并保持5h,然后以5℃/min速率升温至60℃,保持100min,记录陀螺输出,将该组实验数据作为网络的训练数据;

步骤2:重复进行步骤1的操作3次,将这3组实验数据作为网络的验证数据。

步骤1中,陀螺输出零偏、环境温度与谐振子温度随时间的变化关系如图7所示。

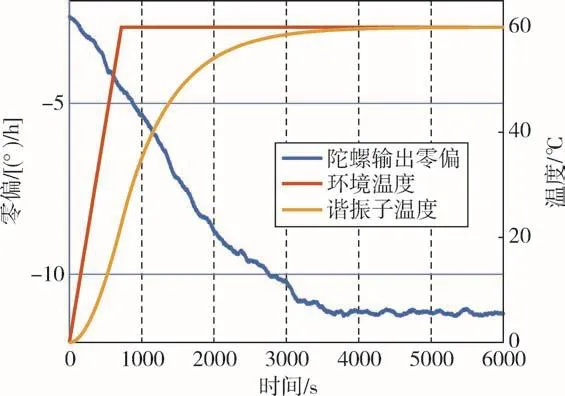
图7 陀螺输出零偏、环境温度与谐振子温度随时间变化曲线Fig.7 Variation curves of gyroscope output bias,ambient temperature and resonator temperature with time

图7中,红色曲线为环境温度变化情况,橙色曲线为谐振子温度变化情况。将图7中零偏随时间变化与谐振子温度随时间变化的数据结合,得到陀螺输出零偏随谐振子温度变化的关系,如图8所示。

图8中,谐振子温度从0℃逼近60℃,陀螺输出零偏由 -2.4497（°)/h 变化到 -11.0213（°)/h。

图8 陀螺输出零偏随谐振子温度变化曲线Fig.8 Variation curve of gyroscope output bias with resonator temperature

由上述分析可知,本实验中BP神经网络的输入节点数m=1,输出节点数n=1,隐含层节点数选为5。BP神经网络的结构为1-5-1,共有权值为1×5+5×1=10个,阈值为5+1=6个,因此遗传算法要优化的数据为10+6=16个。衡量网络优劣的标准选为测试样本的预测值与期望值的误差矩阵范数,将该范数值作为个体的适应度。个体误差范数越小,适应度越高,个体越优秀。遗传算法的各项参数如表1所示。

表1 遗传算法运行参数设定Table 1 Operation parameters setting of genetic algorithm

遗传算法优化的初始权值和阈值的进化曲线如图9所示,在第15代时适应度值达到最小且不再改变,适应度值为20.4624。

图9 遗传算法进化曲线Fig.9 Evolution curve of genetic algorithm

3组遗传算法优化BP神经网络的预测结果及误差分布如图10所示。可以看出,该算法较为准确地预测了陀螺输出零偏与谐振子温度的关系。

图10 3组遗传算法优化BP神经网络预测结果与误差曲线Fig.10 Prediction result and error curves of BP neural network optimized by three groups of genetic algorithms

对该3组实验数据采用最小二乘多项式进行补偿,处理得到的拟合结果与误差曲线如图11所示。

图11 3组最小二乘多项式方法拟合结果与误差曲线Fig.11 Fitting result and error curves of three groups of least squares polynomial methods

两种方法的零偏稳定性比较结果如表2所示。

由表2可知,在进行补偿之后,半球谐振陀螺输出零偏的稳定性得到明显提升。补偿前,3组数据的零偏稳定性均值为2.3833（°)/h;在采用遗传算法优化BP神经网络方法补偿之后,3组数据的零偏稳定性均值优化至0.0772（°)/h;在采用最小二乘多项式方法补偿之后,3组数据的零偏稳定性均值优化至0.1232（°)/h。由以上结果可以看出,相较于最小二乘多项式补偿方法,遗传算法优化BP神经网络方法的补偿效果更好,有效地提高了半球谐振陀螺的输出精度。

表2 最小二乘法与遗传算法优化BP神经网络拟合结果比较Table 2 Comparison of fitting results between GA-BP and least square method

5 结论

本文针对半球谐振陀螺零偏的温度漂移问题,首先推导了谐振子温度与谐振频率的关系;然后,通过建立环境温度到谐振子温度的数学模型,把实验得到的环境温度与陀螺输出零偏的数据转换成谐振子温度与陀螺输出零偏的关系;最后,通过遗传算法优化BP神经网络对陀螺输出零偏进行温度补偿。采用补偿之后,在0℃ ～60℃温度范围内,半球谐振陀螺的零偏稳定性由原来的2.3833（°)/h 优化至 0.0772（°)/h, 达到了提高半球谐振陀螺温度稳定性的效果,对提高半球谐振陀螺的输出精度具有重要意义。