运用线面平行的性质定理求解立体几何试题
福建省龙海第一中学新校区 苏艺伟
立体几何中的综合几何法是高考重点考查的内容.综合几何法对学生的思维要求较高,学生必须将各个公理,定理牢记于心并且学会熟练运用方能解决问题.在众多定理当中,有一个定理是线面平行的性质定理:
若a//α,a ⊂β,α ∩β=b,则a//b.
从该定理的表述当中可以看出,该定理可以帮助我们证明两条直线平行.
在长期的教学中,笔者发现绝大多数学生甚至教师对该定理的重要性认识不够到位,仅仅停留在运用该定理证明简单的线线平行问题.事实上,该性质定理具有非常重要的应用,还可以用来解决立体几何中一些常见的综合性问题.
应用1.确定点的位置
立体几何试题经常涉及点在某条线段上,但是点的具体位置不确定.虽然可以从图形的角度入手,直观感知,猜测点的具体位置,但是不够严谨,缺乏理论依据,仅仅是凭着直觉做出猜测.因此十分有必要以线面平行的性质定理为依据确定出点的具体位置.
例1几何体A1-ABCD中,直线A1A⊥平面ABCD,AB平行等于存在某一个平面α,满足BD ⊂α,A1C//α,直线AA1与平面α的交点为P,若P,A,B,D四个点在同一个球面上,求该球的半径.
试题分析这道题目以四棱锥为载体求几何体外接球半径.题目中的点P是直线AA1与平面α的交点,具体在哪里呢?虽然可以由图1 直观感知点P是线段AA1中点,但是缺乏理论上的支撑.分析题意可知动点P具备如下条件: ①P ∈A1A; ②P ∈面PBD; ③A1C//面PBD.由这三个条件可以确定点P的具体位置.
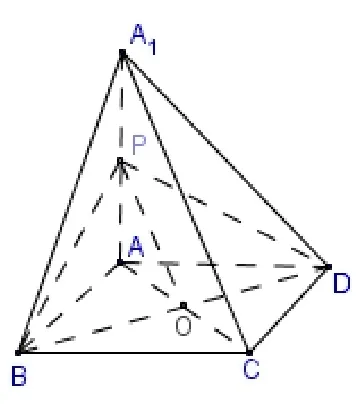
图1
解析如图1 所示,连接AC,BD,交于点O,则O为AC中点.根据线面平行的性质定理,由A1C//面PBD,A1C ⊂面AA1C, 面AA1C∩面PBD=PO, 得PO//A1C.故点P为A1A中点.(后续过程略)
例2已知棱长为1 的正方体ABCD-A1B1C1D1中,线段C1D1上存在一个点E,BD1//面B1CE,则CE的长度为____.
试题分析本题要求的是线段CE的长度, 解题的关键在于确定点E的位置.虽然可以由图2 直观感知点E是线段C1D1中点, 但是这只是感性思维, 缺乏严谨.如何确定点E的具体位置? 要满足:①E ∈C1D1; ②E ∈面B1CE; ③BD1//面B1CE.

图2
解析如图2 所示, 连接BC1, 交B1C于O, 连接OE.由BD1// 面B1CE,BD1⊂面BD1C1, 面B1CE∩面BD1C1=OE得BD1//OE.又点O为BC1中点,则E为D1C1中点,此时
应用2.确定直线与平面位置关系
立体几何强调思维的严谨,要求考生能够从题目所给条件进行严格的推理论证,属于综合法的应用,对促进学生思维能力的提高,孕育数学核心素养具有不可代替的作用.
例3α ∩β=l,A ∈α,C ∈α,B ∈β,D ∈β,A,B,C,Dl,M,N分别是线段AB,CD的中点,下列判断正确的是( )
A.若AB与CD相交,且AC平行于l时,则BD与l可能平行也可能相交
B.若AB与CD不共面,则MN可能与l平行
C.若存在异于AB,CD的直线同时与直线AC,MN,BD都相交,则AB,CD不可能是异面直线
D.存在可能重合的M,N,此时AC与l不可能相交
试题分析本题给出了较为复杂的点,线,面位置关系,要求综合应用公理(基本事实),判定定理,性质定理解决问题,对学生的推理论证能力提出了较高的要求.学生必须对相关的定理有十分清楚的认识并学会应用.对于A 选项,结合题目条件,可以借助直线与平面平行的性质定理进行判断.
解析当AB与CD相交时,A,B,C,D四点在同一个平面上.因为AC//l, 所以AC//β.因为AC//β,AC ⊂面ABCD, 面ABCD∩面β=BD, 故AC//BD.故BD//l.从而A 答案不正确.本题选D(请读者自行完成).
例4已知直线a和b既不平行且不相交,a ⊂α,b ⊂β,a//β,b//α,证明α//β.
试题分析本题虽然条件简单实则综合性强.必须在结合图形的基础上,充分发挥空间想象能力,以公理定理为依据解决问题.
解析设点O是直线b上的一个点,此时a与点O可以确定一个平面γ,设β ∩γ=l.由a//β,a ⊂γ,β ∩γ=l得a//l.由l//得l//α.由l//α,b//α,l ∩b=O得α//β.
应用3.两个平面的交线问题
对于立体几何中涉及到两个平面的交线问题,需要对交线与其余几何元素的位置关系做出判断.此时不一定要知道交线的具体位置,只需以线面平行的性质定理为依据证明出该交线与其余几何元素的位置关系即可.
例5在如图3 所示的正方体ABCD-A1B1C1D1中,面BDP∩面B1D1P=m,棱AA1的中点为Q,棱CC1上有一个动点P,则( )
A.m//D1QB.m//面B1D1Q
C.m ⊥B1QD.m ⊥面ABB1A1
解析如图3 所示, 由B1D1//BD,BD ⊂面BDP,B1D1面BDP, 得B1D1// 面BDP.由B1D1// 面BDP,B1D1⊂面D1B1P, 面BDP∩面D1B1P=m, 得B1D1//m;又B1D1⊂面B1D1Q,所以m//面B1D1Q,故选B.
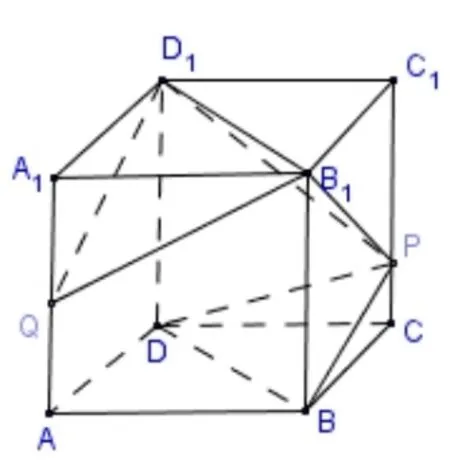
图3
例6在如图4 所示的几何体ABC-A1B1C1中,AA1⊥面ABC,线段BC的中点是D,AB的中点是E,棱CC1上有一个动点F,AB=BC=CA=CF=2,AA1=3,下列说法中正确说法的序号为____.
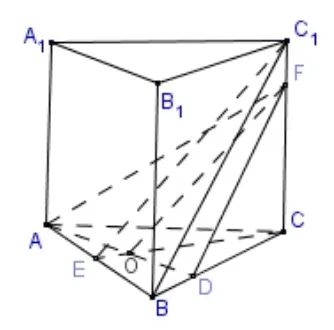
图4
(1)若面ADF∩面BEC1=l,则C1E与l相交
(2)三棱锥N -ADF的体积可以为,其中点N在棱A1C1上
(3)设点M在BB1上,当BM= 1 时,平面CAM ⊥平面ADF
(4)在棱A1B1上存在点P,使得C1P ⊥AF
解析如图4 所示, 对于(1)的判断, 连接AD,CE,交于点O, 则O为ΔABC重心.由得OF//EC1.由OF//EC1,EC1⊂面BEC1,面BEC1, 得OF// 面BEC1.由OF// 面BEC1,OF ⊂面ADF,面ADF∩面BEC1=l,得OF//l.所以l//EC1.故(1)错误.本题选(3),理由从略.
上述两道试题都涉及到两个平面的交线问题,求解策略并不是直接作出交线,而是化抽象为具体,化复杂为简单,在认真观察图形的基础上综合应用直线与平面的性质定理来解决问题.
应用4.其余综合性问题
例7如图5 所示, 已知点P是正方体ABCD-A1B1C1D1底面ABCD两条对角线的交点,A1D1上有一个异于端点的动点E,AE的中点为Q.则: (1)PE//面CDD1C1,(2)面APE ⊥面BDD1B1,(3)PE与QC既不平行也不相交,(4)假设截面经过A,P,E三点,则截痕是等腰梯形,正确的有____.
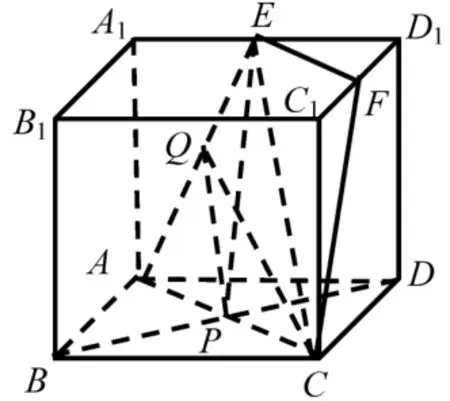
图5
解析对于(1),以线面平行的性质定理为依据来判断.假设PE//平面CDD1C1.由PE//面CDD1C1,PE ⊂面ACFE, 面CDD1C1∩面ACFE=CF, 得PE//CF.又EF//PC,所以四边形PCFE为平行四边形,故EF=PC.由于点P为AC中点,所以点E为A1D1中点.这与点E为线段A1D1上的动点矛盾.因此PE//平面CDD1C1不成立.
对于(4), 同样以线面平行的性质定理为依据来判断.由面ABCD//面A1B1C1D1,α∩面ABCD=AC,α∩面A1B1C1D1=EF,得EF//AC.故必须作EF//A1C1,才能确保EF//AC(平行线间的传递性,基本事实4).进一步得到截面α即为等腰梯形ACFE.余下从略.
本题中,要判断PE//平面CDD1C1是否成立,虽然能够基于图形的角度简要判断,但是不利于培养学生严谨的逻辑推理能力,教师必须以定理为依据将基于感觉的表象通过严谨的证明体现出来,让学生深刻地体会到逻辑推理的重要作用.
不难发现,线面平行的性质定理确确实实在解决立体几何问题中起到了重要的作用.这就要求教师在平时的教学中,尤其是高三年的复习课当中,要注重对公理(基本事实),判定定理,性质定理的教学,在讲透的基础上借助典型试题加以应用,不能停留在简单的层面,必须通过严格的推理论证来实现,唯有如此,才能引领学生的思维走向深处,促进深度学习,真正践行课标理念.

