机械波多解问题中的解法“套路”
宁夏 龚 杰 马文学
机械振动在介质中传播,形成了机械波。由于波源在介质中的起振方向和传播方向的不确定,就导致波动问题的多解性。分析多解问题的方法有很多,笔者就此类问题给出一种“套路”式的解法,仅供参考。
一、波动问题多解的分类
1.周期性
(1)振动时间间隔Δt与周期T的关系不明确造成多解问题
在x轴上取一个质点,其在t时刻的振动情况与它在t+nT,(n=1,2,3…)时刻的振动情况(位移、速度、加速度等)相同,这就是机械波的时间周期性。波的时间周期性表明,波在传播过程中,经过整数倍周期时,其波形图线相同。因此当振动时间间隔Δt远大于周期T时,某一时刻的波形必然多次出现,这就是振动时间间隔Δt与周期T的关系不明确造成多解问题的原因。
(2)传播距离Δx与波长λ的关系不明确造成多解问题
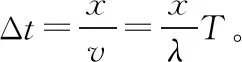
图1
2.双向性
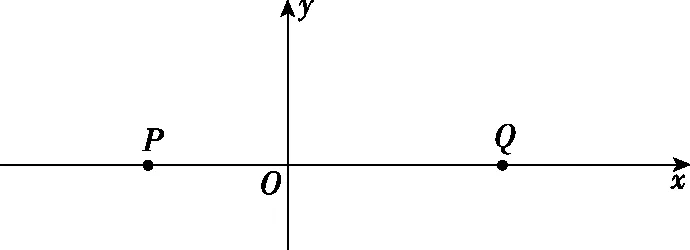
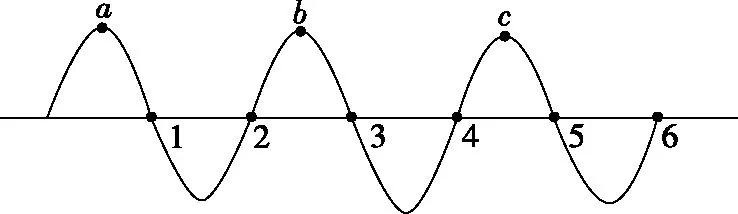
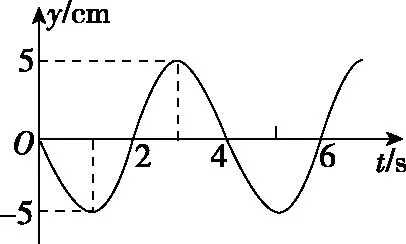
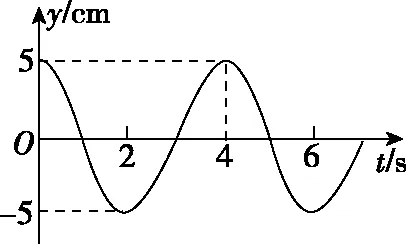
通常在坐标轴上,波可沿正、负两个方向传播。若沿正方向与负方向传播的时间之和等于周期的整数倍,则沿正或负方向传播对应的波形图相同,如图2中的实线是一列正弦波在某一时刻的波形图,经过Δt时间后(Δt 图2 3.波形的隐含性 波动问题中,在波的传播方向上,如果两个质点间的距离不确定,或者题目中只给出完整波形的一部分,又或者只给出几个特殊点的振动情况,而其余信息均处于隐含状态,波形就有多种情况,形成波动多解的问题。 图3 1.根据初末两时刻的波形图确定传播距离与波长(传播时间与周期)的关系通式。一般采用从特殊到一般的思维方法,即找出一个周期内满足条件的关系Δt或Δx。 若此关系为时间: 可得有关周期的通式: 若此关系为距离: 可得有关波长的通式: 【例1】上文图2中的实线是一列正弦波在某一时刻的波形曲线。经过0.5 s后,其波形图如图中虚线所示。 (1)如果波是向左传播的,周期多大?波速多大? (2)如果波是向右传播的,周期多大?波速多大? 【分析】根据题图可知该波的波长λ=0.24 m,这列波经过0.5 s后的波形图从实线变成了虚线,可以根据0.5 s内波形图确定传播时间与周期(距离与波长)的关系通式进行求解。 解法一:由波形图可根据传播时间与周期的关系进行求解 (1)若波向左传播:则 将Δt=0.5 s带入周期的通式可得: 又λ=0.24 m,则 (2)若波向右传播:则 将Δt=0.5 s带入周期的通式可得: 又λ=0.24 m,则 解法二:由波形图可根据传播距离与波长的关系进行求解 (1)若波向左传播:则 又λ=0.24 m,则 v=0.12(4n+1) m/s,(n=0,1,2,3…) (2)若波向右传播:则 又λ=0.24 m,则 v=0.12(4n+3) m/s,(n=0,1,2,3…) 2.若在波动问题中,没有给出波形图,只给出波形上几个特殊点及与质点相关的振动方程或振动图像。此时可用逆向思维,根据一个未标注横轴和纵轴的波形加以题设条件得出大致波形图,在波形图上找到符合题设条件的特殊点,然后根据波形图确定传播距离与波长(传播时间与周期)的关系通式进行求解。 ( ) A.如果波沿x轴正方向传播,则波长的最大值为2 m B.如果波沿x轴正方向传播,则波速的最大值为1 m/s D.t=4.5 s时刻,Q点离开平衡位置的位移为4 cm 现给出任一波形图,如图4所示,在图中a、b、c可能是P点所在的位置,图中1、2、3、4、5、6可能是Q点所在的位置。若波沿x轴正方向传播,根据Q点振动方程可知,下一时刻其振动方向由平衡位置向y轴正方向振动,此时Q点的位置则可能是1、3、5。根据P、Q间距离与波长的关系可得: 图4 若波沿x轴负方向传播,根据Q点振动方程可知,下一时刻其振动方向由平衡位置向y轴正方向振动,此时Q点的位置则可能是2、4、6。根据P、Q间距离与波长的关系可得: 【答案】BC 【例3】一列简谐横波沿x轴传播,已知x轴上x1=1 m和x2=7 m处质点振动图像分别如图5、图6所示,则此列波的传播速率可能是 图5 图6 ( ) A.7 m/s B.2 m/s C.1.2 m/s D.1 m/s 【解析】现给出任一波形图,如图7所示,在t=0时,图中1、2、3、4、5、6可能是x1=1 m质点所在的位置,图中a、b、c可能是x2=7 m处质点所在的位置。若波正在沿x轴正方向传播,根据x1=1 m振动图像可知,其离开平衡位置向y轴负方向振动,则此时2、4、6可能是x1=1 m处质点的位置。根据x1=1 m和x2=7 m间距离与波长的关系可得: 图7 又T=4 s,则 若波正在沿x轴负方向传播,根据x1=1 m振动图像知其离开平衡位置向y轴负方向振动,则此时1、3、5可能是x1=1 m处质点的位置。根据x1=1 m和x2=7 m间距离与波长的关系可得: 又T=4 s,则 若波沿x轴正方向传播,当n=0时,v=2 m/s,若波沿x轴负方向传播,当n=1时,v=1.2 m/s,综上分析答案为BC。 【答案】BC 从以上的讨论可以发现,对于机械波图像中多解性问题的解法是一种“套路”式的解法,总结起来就是:利用题设条件的波形图,或者根据题设条件构建出波形图,根据波形图找到符合题设条件的特殊点,然后确定传播距离与波长(传播时间与周期)的关系通式进行求解。本文中几道典型例题中构建的距离与波长(传播时间与周期)的关系只是四分之一或者四分之三的关系,实际还有大量机械波多解问题中距离与波长(传播时间与周期)的关系更复杂,这类试题我们可采用类似的“套路”具体问题具体分析即可。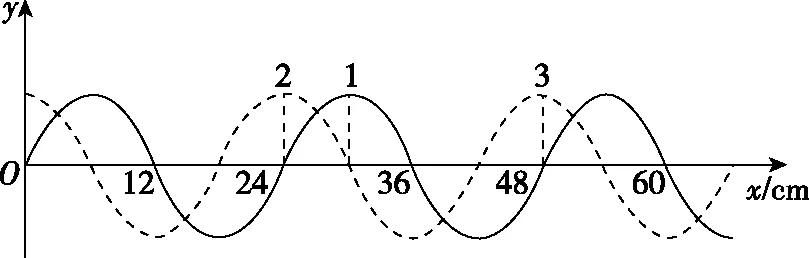
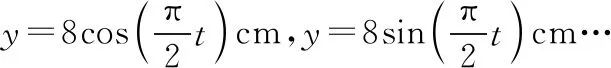
二、波的多解问题的“套路”解法
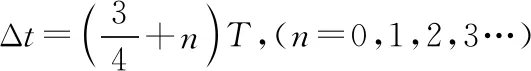
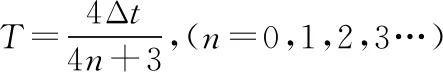
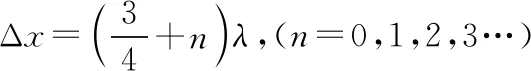
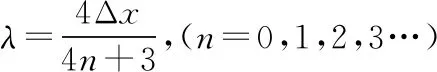
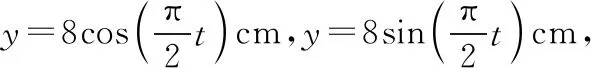
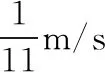
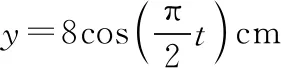
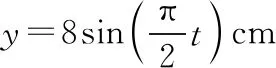
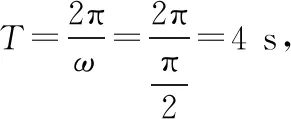
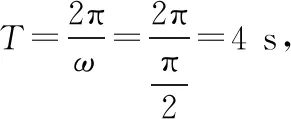
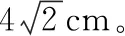

三、结束语

