关于惠更斯对向心加速度证明方法的思考与应用

鲁 斌 冯子江

（浙江省余姚中学 浙江 宁波 315400）

在人教版高中物理教材“向心加速度”一节中［1］，编者利用加速度的定义对“向心加速度公式”进行了详细的推导，此推导过程充分体现了矢量和微分的思想.在课堂教学中，还可以提供荷兰物理学家惠更斯（Christiaan Huygens，1629-1695）当年的推导方案，启发学生对此问题进行更加深入的思考.

1 引出推导方案

在人教版高中物理教材“向心力”这一节有这样一段话：“运动轨迹既不是直线也不是圆周的曲线运动，可以称为一般的曲线运动.尽管这时曲线各个位置的弯曲程度不一样，但在研究时，可以把这条曲线分割为许多很短的小段，质点在每小段的运动都可以看作圆周运动的一部分（图1）.这样，在分析质点经过曲线上某位置的运动时，就可以采用圆周运动的分析方法来处理了.”

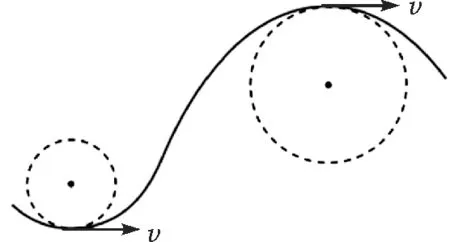
图1 一般曲线运动的轨迹

这段文字表达了“曲率圆”的概念.反过来，我们也可以启发学生思考：既然一般曲线运动的每一小段都看做圆周运动的一部分，那么，圆周运动的每一小段是否也是一般曲线运动的一部分呢？

2 天文学家、数学家惠更斯的工作再现

荷兰物理学家、天文学家、数学家惠更斯在1673年发表的《Horologium Oscillatorium》附录中给出了离心力的完整计算方法［2］，由此可以大致总结其对向心加速度的推导方案.

如图2所示，如果没有加速度，质点在短时间Δt内从A以速度v匀速运动到B，实际上质点做圆周运动，在Δt时间内从A运动到C，可以认为这是由于质点同时参与了另一个由B到C的匀加速运动而导致的，所以有

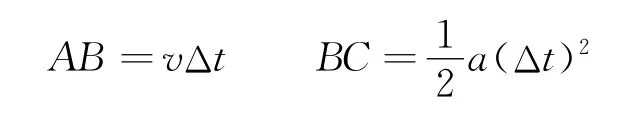
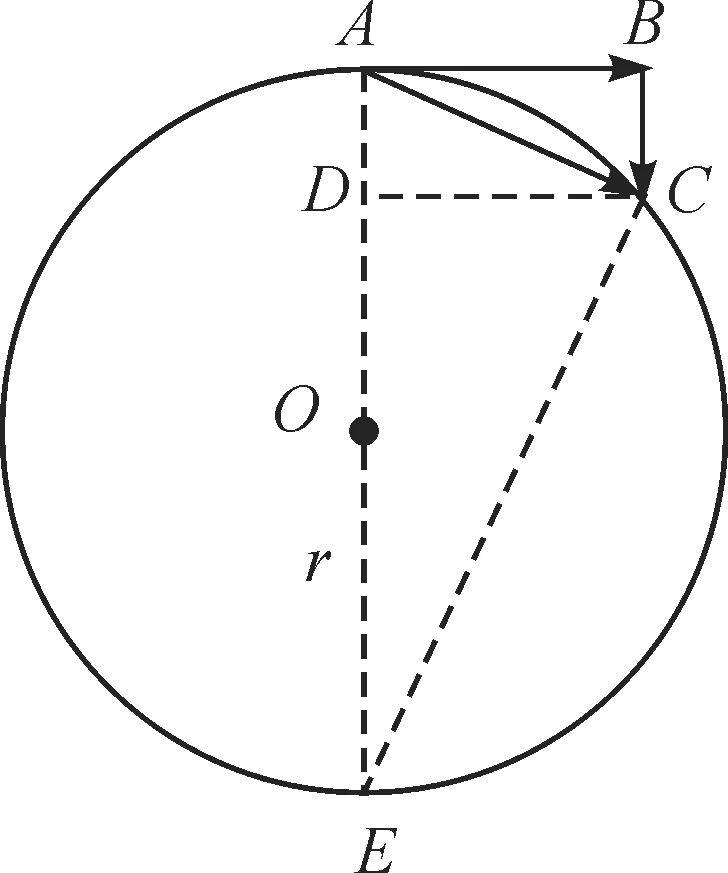
图2 向心加速度推导示意图

圆周运动半径为r，由于△ABC∽△EDC有

可得a=，当Δt→0时，方向指向圆心，故将这个加速度称为向心加速度.

3 苹果和月亮的思考

牛顿在乡下故居躲避瘟疫的时候，开始认真关注苹果下落的问题［3］.牛顿的沉思是：月球为什么不像苹果那样，落到地面上来呢？经过一段时间的思考，牛顿明白了：月球不落到地面上来，是因为它在绕地球旋转；即使是苹果，如果它以适当的速度运动，也照样不会落到地面上来，同样会绕地球旋转.月亮绕地球转动，实际上也可以看成是种“下落”（图3），只不过没有落到地球上来，而是保持一定距离绕着地球转.如果月球不是不断地“下落”，它就会离开地球，飞到浩瀚的宇宙深处.

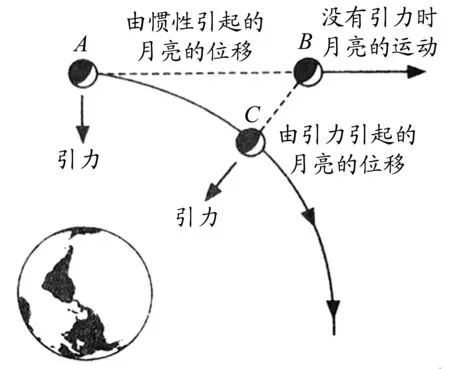
图3 月球“降落”的示意图

圆周运动也是一种“降落”，让我们对运动有了进一步的理解.圆周运动与直线运动并不是相互独立的，而是彼此统一的.在课堂中，我们可以做如下的推导.

如图4所示，假设一人造卫星在近地轨道做半径为r，角速度为ω的匀速圆周运动，在t时间内从A点运动到D点，扫过的圆心角θ=ωr.则有

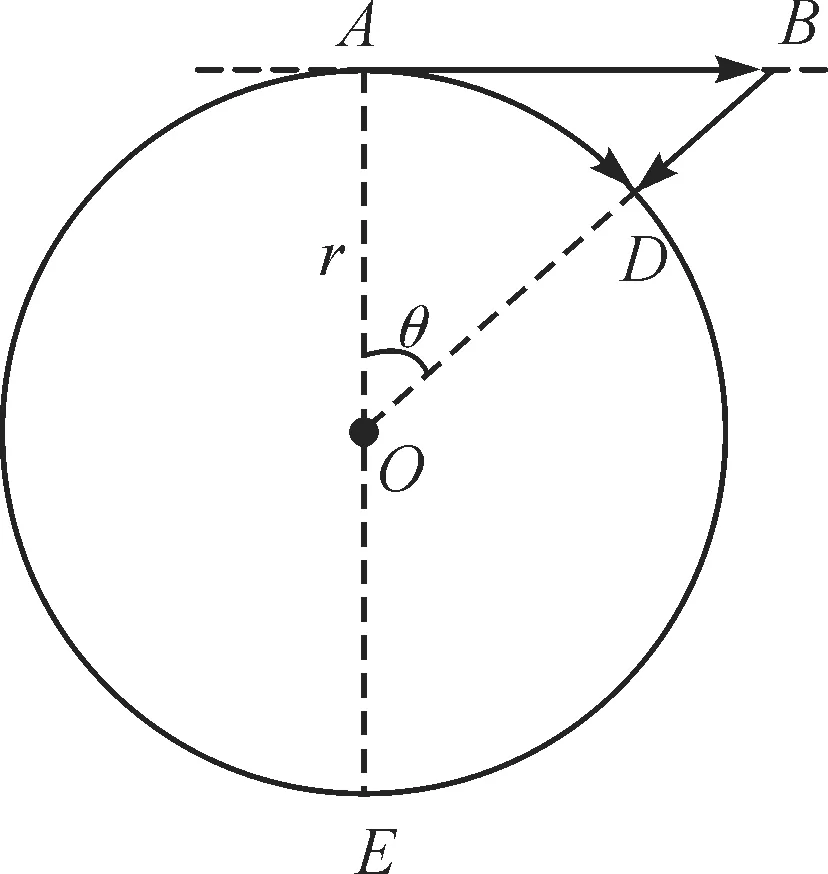
图4 圆周运动实际上是一种“降落”

月球在径向做的是“自由落体运动”.

4 运动的叠加

由于圆周运动可以看做是匀速直线运动与匀变速直线运动的叠加，在极短时间内的速度变化如图5所示.即

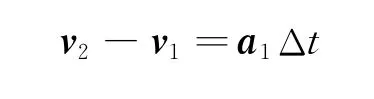
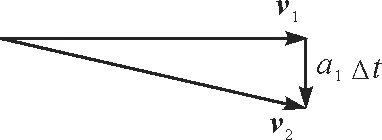
图5 单次叠加

对于匀速率圆周运动，由于叠加只引起速度方向的改变，则多次叠加过程如图6所示.有

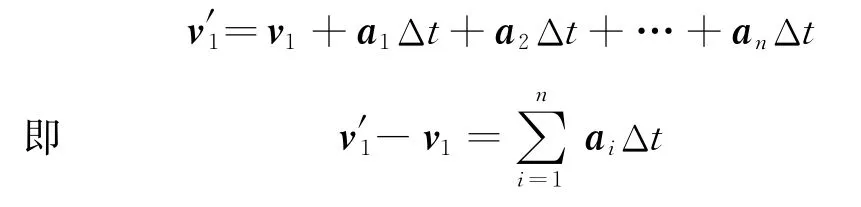
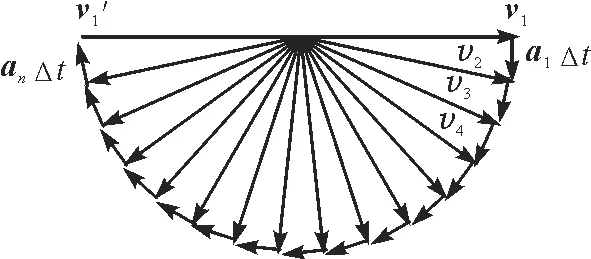
图6 多次叠加

若将Δt→0，则整个速度变化的过程即为连续的（图7）.

海淀区东片数学区域教研组根据教师的实际教学情况及需求，对各个阶段的教研活动进行了细致分析与精心设计。以上教研活动各有特点和作用，各项活动相辅相成。

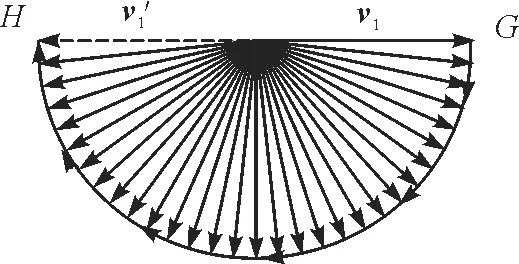
图7 连续叠加

速度矢量从v1到的过程，即为图4中从最高点A到最低点E的过程.则

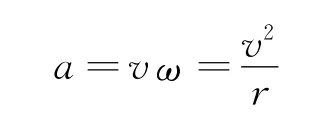
5 应用

从上面的推导可以看出，在极短时间内，圆周运动与抛体运动的规律是一样的.在相同大小的力的作用下，物体可以做圆周运动，也可以做平抛运动，他们在极短时间内，看起来是同一种运动.满足相同的运动学规律.我们可以将此思路应用于浙江省2021年1月份选考试题压轴题的解答［4］.

【试题】在芯片制造过程中，离子注入是其中一道重要的工序.如图8所示是离子注入工作原理示意图，离子经加速后沿水平方向进入速度选择器，然后通过磁分析器，选择出特定比荷的离子，经偏转系统后注入处在水平面内的晶圆（硅片）.速度选择器、磁分析器和偏转系统中的匀强磁场的磁感应强度大小均为B，方向均垂直纸面向外；速度选择器和偏转系统中的匀强电场场强大小均为E，方向分别为竖直向上和垂直纸面向外.磁分析器截面是内外半径分别为R1和R2的圆环，其两端中心位置M和N处各有一个小孔；偏转系统中电场和磁场的分布区域是同一边长为L的正方体，其速度选择器底面与晶圆所在水平面平行，间距也为L.当偏转系统不加电场及磁场时，离子恰好竖直注入到晶圆上的O点（即图中坐标原点，x轴垂直纸面向外）.整个系统置于真空中，不计离子重力，打在晶圆上的离子，经过电场和磁场偏转的角度都很小.当α很小时，有sinα≈tanα≈α，cosα≈1-.求：

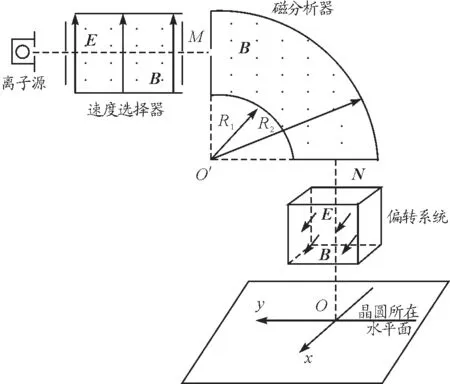
图8 离子注入工作原理示意图

（1）离子通过速度选择器后的速度大小v和磁分析器选择出来离子的比荷；

（2）偏转系统仅加电场时离子注入晶圆的位置，用坐标（x，y）表示；

（3）偏转系统仅加磁场时离子注入晶圆的位置，用坐标（x，y）表示；

解：（1）通过速度选择器离子的速度v=，从磁分析器中心孔N射出离子的运动半径为

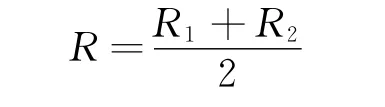
由牛顿第二定律

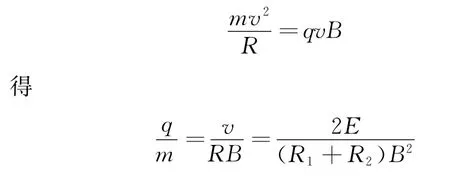
（2）经过电场后，离子在x方向偏转的距离

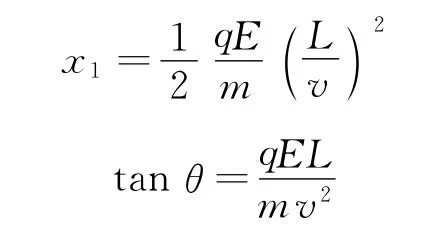
离开电场后，离子在x方向偏移的距离

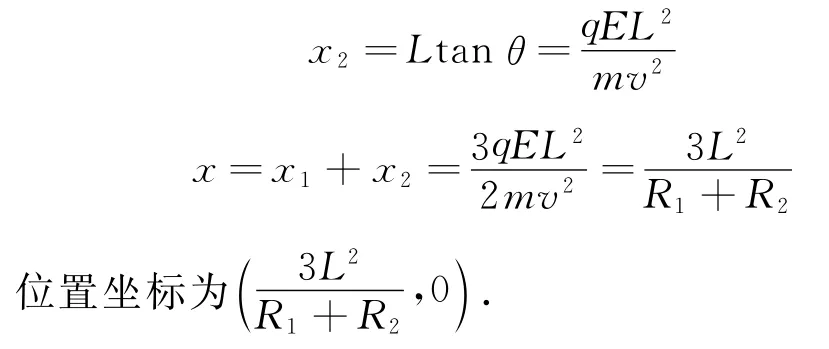
（3）方法1：如图9所示，离子进入磁场后做圆周运动的半径

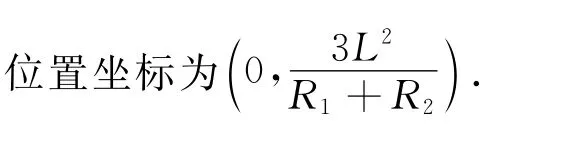
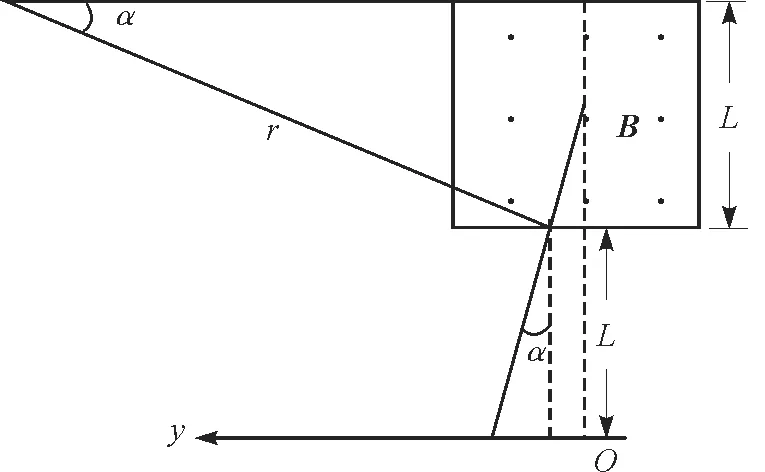
图9 磁场偏转示意图

方法2：由于物体所受到的电场力和洛伦兹力的大小一样，虽然此时一个是圆周运动，但在极短时间内，力的方向并没有发生改变，可以当做恒力处理，故在极短时间内仍然与抛体平抛运动产生的位移变化、速度变化一致，则可直接写出答案，即位置坐标为

评析：本题的最大难点在于磁场运算时的小量近似，由于近似过程比较陌生，学生答题的正确率并不高.可以从本文的角度进行考查，在极短时间内，曲线运动的轨迹既可以当做平抛运动来处理，又可以当做圆周运动来处理.所以，这两者解答的结果必然是相同的.明白了这一点，只要做出第（1）、（2）小题，第（3）小题便可直接写出答案，根据运动的独立性，也可直接写出第（4）小题的结果，节约了大量时间，并提高了解题的正确率.