盾构隧道施工引起地表沉降的“五维”空间效应探索及其展望

于广明，雷 军，张鹏辉，陈 泽，梁冠文

(1.青岛理工大学 土木工程学院，青岛 266525；2.中国建筑第五工程局有限公司，长沙 410007；3.中国建筑五局华南公司，广州 510000)

1 问题的提出

地铁的建设既为现阶段人们的出行提供了方便，也为将来城市地下空间的统一规划和建设留下伏笔。然而，地铁隧道施工过程中不可避免地会对地层产生扰动，造成地表沉降等地质灾害，无论是对于地下管线还是地面已有建筑物都有不容忽视的影响，在某些复杂地质条件下甚至会造成更大的危害，如图1所示，社会危害和经济损失极其严重，已成为当今社会的热点问题和隧道施工安全的重大难题，迫切需要地铁隧道施工引起的地表沉降安全管控的分析理论与方法。因此，研究隧道施工引起地表沉降的机理和规律，进而在此基础上研制隧道施工引起地表沉降的控制措施，社会效益、工程价值及其科学意义均十分明显。

图1 隧道施工引起地表沉降的危害

对于隧道施工引起的地表沉降特性及发展演化规律问题，国内外学者已有一定研究，PECK[3]在总结大量现场实测数据的基础上提出地表沉降满足高斯正态分布曲线，且认为地表沉降现象是由地层损失导致的，在不排水的条件下地表沉降槽体积与地层损失体积相同；刘宝琛等[4]对波兰学者LITWINISZYN提出的随机介质理论进行了进一步扩展，将岩土体当作一种随机介质，建立了地表沉降计算的概率积分法，解决了地下开挖引起的地表沉降预测问题；王璐[5]研究了盾构隧道施工步长对地表沉降槽形状的影响，得出大步长的沉降量相比小步长的沉降量大的结论；赵旭伟[6]研究了地层变形的空间效应和时间效应，分析了在时间轴上地表沉降槽的发展历程；侯学渊等[7]通过将固结效应引起的附加沉降作为地层损失的一部分，对Peck公式做出修正，将地表沉降槽随时间的演化规律通过公式的方法进行了描述；AHMED等[8]通过透明模型试验模拟了隧道开挖过程，并认为受扰动的岩土体颗粒位移矢量指向隧道轴线下方仰拱附近或隧道中轴线方向。夏元友等[9]通过使用位移矢量方法研究了盾构施工引起的地表土体水平位移特性，在验证了AHMED结论的正确性后，又提出了位移矢量角的概念。高守栋等[10]研究了地面出入式盾构隧道对周围地层的扰动效应，验证了地面位移与空隙水压力之间的变化关系。秦东平等[11]利用三维非线性有限元模型和相关解析理论，研究了地铁修建过程中地表变形规律。然而，上述学者多数是在X，Z两个维度或X，Y，Z三个维度上分析和认识隧道施工引起地表沉降的展布，在三维空间中将盾构隧道施工引起地表沉降视为槽型，称之为地表沉降槽，研究沉降槽在横剖面和纵剖面上的几何特性，例如Peck公式研究的是地表在不排水条件下沉降槽在横剖面上的几何特性，对于沉降槽形状随步长和时间的演化则没有描述；少数学者对隧道施工引起地表沉降的时间效应进行了研究，初步涉及了隧道施工引起地表沉降在X，Y，Z，T四个维度上的演化问题。

但是，现场工程实践证明，如深圳地铁13号线留仙洞—白芒区间盾构隧道施工，地表沉降除了在X，Y，Z三个维度上展布且随着时间T维度发展以外，还随着掘进步长L这个维度不断地演化，若想更加深入、更加精细认识和研究隧道施工引起地表沉降的复杂性，需要根据盾构隧道施工的特点及其引起地表沉降的真实过程，进一步研究地表沉降在掘进步长L维度和时间T维度上的演化特征和规律。因此，本文拟将隧道掘进步长L维度和时间T维度分离，探究地表沉降随盾构隧道掘进步长和时间两个维度的演化规律，揭示盾构隧道施工引起地表沉降的“五维”空间效应。

自然界中“五维”空间是否存在，能否在“五维”空间中认识和研究自然现象，目前仍是科学之谜，在这方面只有少数科学家有过揭示和研究，WESSON等[12]通过对电磁与引力两大基本力统一模型的研究，将广义相对论延申至五维空间，并得出一个五维度规张量的纯量场；PRATEEK等[13]通过对实验中微粒的观察，发现有部分微观粒子跃迁到了人类“看不到的空间”，它们其实离我们并不遥远，只是很好地隐藏了起来，PRATEEK将这个“我们看不到的空间”称为“第五维空间”。可见国际上学术界对“五维”空间的认可。所以，就自然现象的空间维度来讲，可以肯定地说“分维是真例，整维是特例；三维、四维是暂时的，多维(分维、大于四维)是长远的”，地表沉降现象的分维特征和多维性是其存在的必然，建立盾构隧道施工引起地表沉降的空间-步长-时间“五维演化理论”将成为可能[14]。

2 盾构隧道施工引起地表沉降的维度问题

2.1 地表沉降的二维阐述

隧道施工引起地表沉降是被扰动波及的地表上所有点的群体位移效应，不过最初为了工程方便或研究手段的限制，只分析隧道横剖面上地表点的位移，即沉降曲线，如图2所示；对某个地表点来讲，其位移为指向隧道中心的矢量，分为沿垂直方向(Z)的“下沉”和沿水平方向(X)的“水平移动”。同理，对于隧道纵剖面上地表点的沉降表示也仅分析沿垂直方向和水平方向两个维度的沉降曲线，此时一般只研究沿隧道中心线的纵剖面上地表点的沉降，如图3所示。

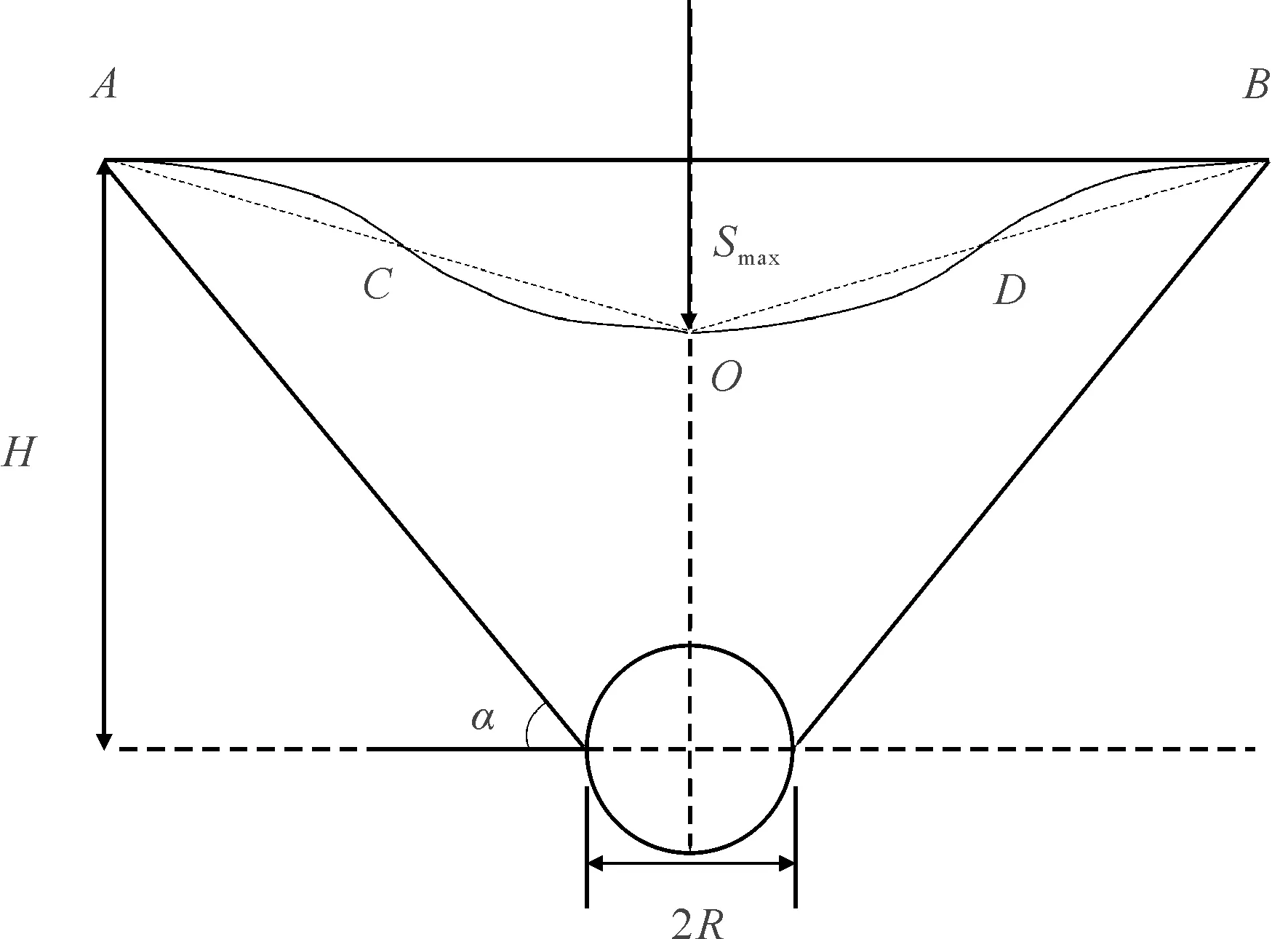
图2 二维空间中地表横向沉降曲线

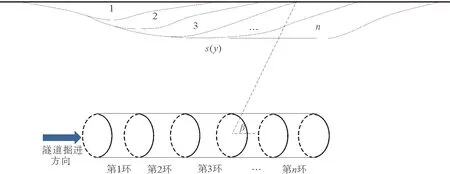
图3 二维空间中地表纵向沉降曲线

2.2 地表沉降的三维阐述

然而，受隧道施工的扰动，地表点移动轨迹始终指向隧道开挖工作面的中心，其移动矢量在X，Y，Z三个维度上都有分量，如图4所示，隧道施工结束且地表稳定后，在地表形成三维的地表沉降槽，在隧道横向X、纵向Y和垂直方向Z三个维度上展示着其发展特征，对于三维空间中的地表沉降则是上述二维空间中地表沉降曲线的“空间组合”，其形状为中间深，两侧浅的沉降槽，如图5所示。

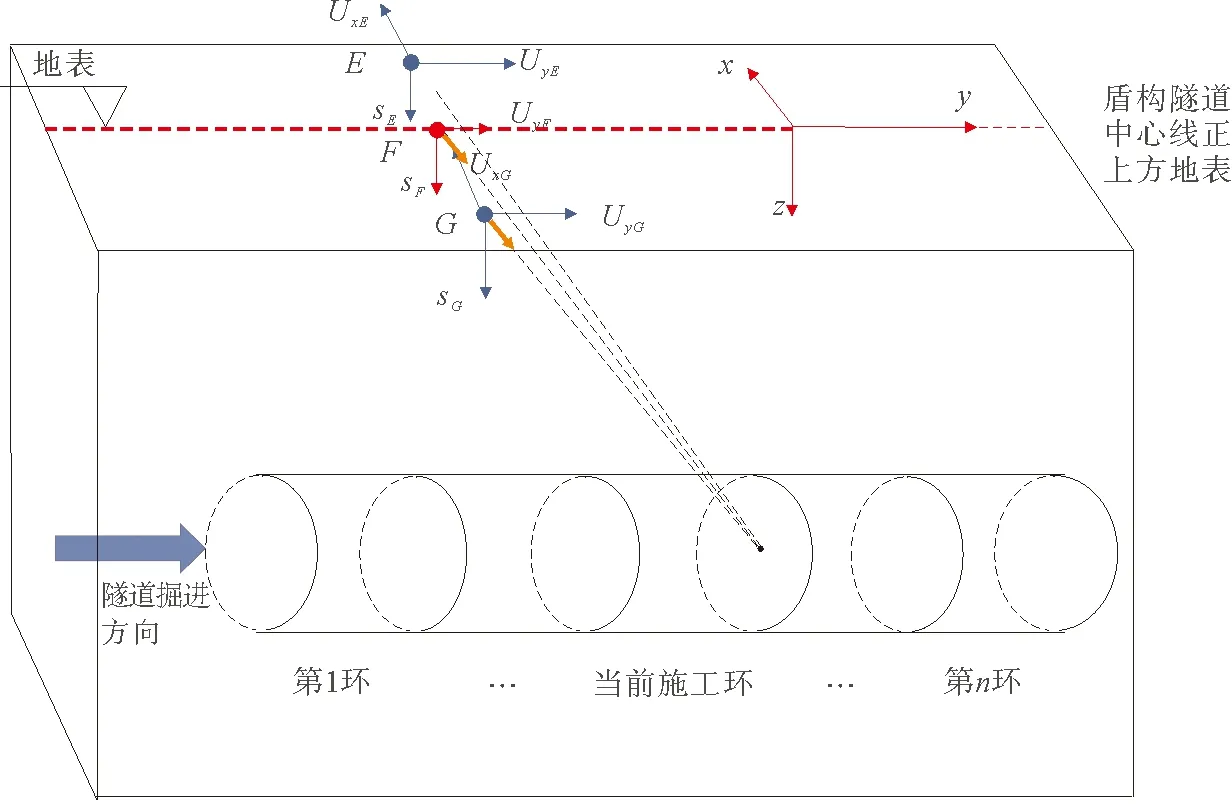
图4 三维空间下隧道施工地表沉降位移矢量示意

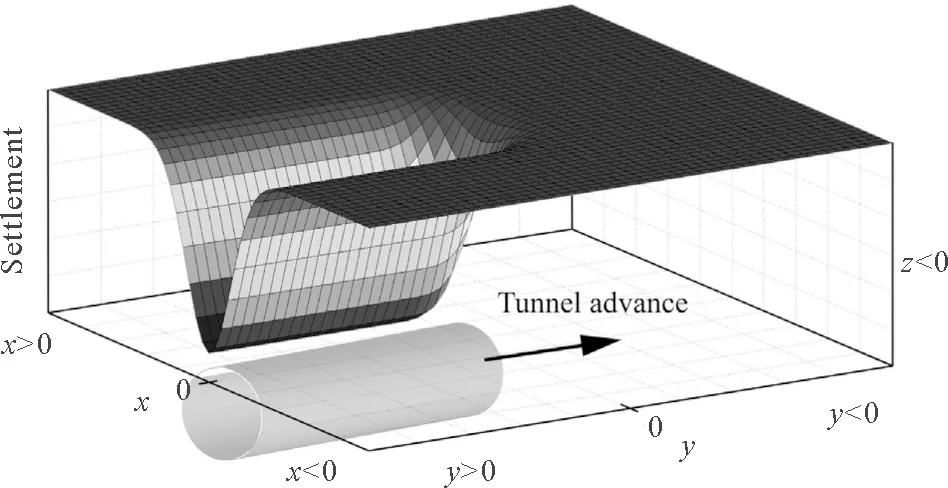
图5 三维空间中地表沉降槽曲面[15]

2.3 地表沉降的四维阐述

对于盾构隧道施工引起地表沉降问题，盾构机掘进步长(L)是一个重要的影响因素。不难理解，随着盾构机的向前推进，上述三维的地表沉降槽不断演化并向前扩展，在三维空间中引入第四个维度，即盾构机掘进步长轴，研究三维沉降槽在步长轴(L)上的展布特征和发育规律，即地表沉降的“四维”效应，如图5所示。

对于地表沉降槽随盾构机掘进步长演化的证据还可以由地表上任意一点的移动轨迹来说明。选沿隧道中心线纵剖面上地表上A点，其位移矢量轨迹始终指向隧道掘进工作面的中心，紧随盾构推进步长(盾构环数)而发展演化，如图6所示。地表沉降槽随盾构推进步长发展演化恰是受扰动所有地表点随盾构推进步长演化的群体效应。

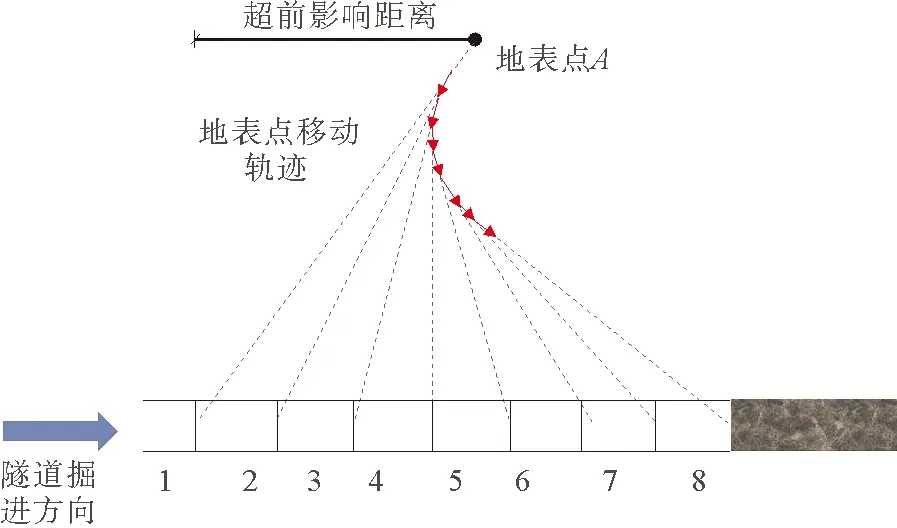
图6 地表沉降条件和隧道中心线纵剖面上地表任意一点的移动路径[14]

2.4 地表沉降“五维”空间中“时间轴”诠释

ALBERT在1905年研究狭义相对论时，提出了“时间和空间的相对性”“四维时空”“弯曲空间”等全新的概念。将时间和空间结合在一起，盾构隧道施工引起地表沉降“五维”空间中的时间轴诠释也是以此为基础。

地表沉降槽不仅随着盾构机的向前推进而不断向前扩展，而且其数值还会随着时间(T)的推移而不断发展增大，直至增大到隧道施工特定条件下(地质条件、隧道埋深、隧道尺寸、隧道施工工艺过程)的最大值。

事实上，盾构隧道施工引起的地表沉降取决于2个条件，一是隧道施工在地层中形成的临空体，二是隧道上覆岩土层的重力，隧道施工在地层中形成临空体后，上覆岩土层就会在重力作用下向着临空体中心产生移动，发展到地表即为地表沉降，这是一个临空体积不断向上传递的时间过程，即本文将其视为的第五个维度——时间轴(T)。

在实际工程中，盾构机掘进步长是由推进环数来计量的，也即每环管片的长度，我国隧道管片的长度一般有1.0，1.2，1.5 m 3个尺寸，盾构机每当掘进一环，便停机安装管片，此时隧道停止掘进，停机时间为1 h左右，即使在停机状态，地表点的沉降仍然随着岩土层中的临空体积向上传递、运动扩散[16]，岩土层固结不断地发生着，其时间效应仍然存在，也即在推进环数维持不变的情况下，地表沉降槽仍然随着时间的延续而发生不断的演化，所以将时间因素考虑在内综合研究地表沉降槽的形成发展过程以及最后的地表沉降槽几何特征是至关重要的。

综上所述，地表沉降的“五维”空间效应是指在地表沉降槽的三维几何特征(X，Y，Z)表述的基础上，地表沉降槽在步长轴(L)和时间轴(T)上的演化过程。

因此，将盾构机掘进步长和时间作为两个维度，研究地表沉降槽的演化规律更为合理，如图7所示。

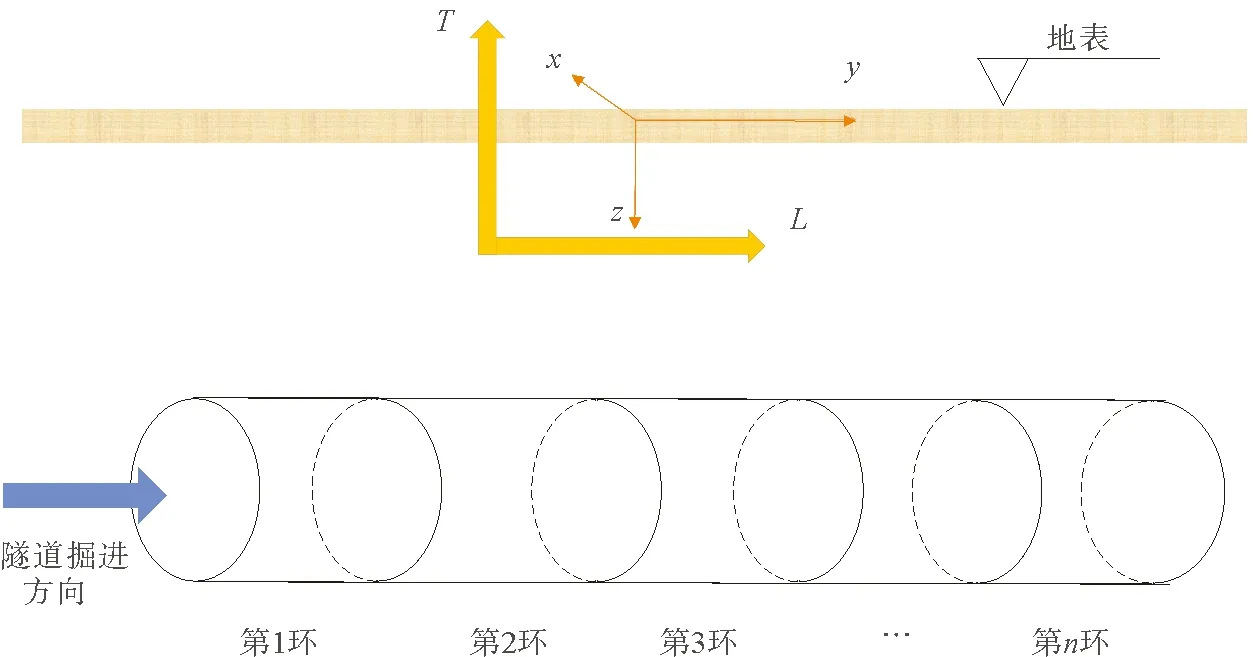
图7 五维空间下隧道沉降模型坐标系示意

3 各维空间中地表沉降的特征表征

3.1 二维空间中(横纵剖面)地表沉降几何特征

二维空间中，地表沉降通过曲线的形式进行展现，故将地表沉降在二维空间中的表现形式定义为“沉降线”，依据概率积分法的几何特征点与特征参数，如图2所示：

1) 最大下沉点O。最大下沉点为地表沉降曲线上最大下沉值的点，对于单洞隧道施工来讲，一般位于隧道开挖断面的正上方。

2) 沉降边界点A，B。盾构隧道施工对地表产生的影响是从隧道中心处向两侧逐渐递减的。盾构隧道施工对地表不再产生扰动的最近点，即为沉降的边界点。

3) 拐点C，D。拐点是指沉降曲线凹凸的分界点，其位置一般在隧道围岩明显变形区域的外边缘的正上方，拐点C，D处的地表下沉值一般是地表最大下沉值的一半。

4) 隧道施工影响范围。地表沉降两侧边界点内的区域即为隧道施工对地表的影响范围。隧道开挖的影响范围与岩层状态相关，一般用主要影响角正切值来反应。

5) 主要影响角α。沉降曲线外边缘至隧道开挖断面最外轮廓线底部连线与水平线的夹角称为主要影响角，如图2中角α。

6) 超前影响角β。盾构工作面前方地表开始移动的点与工作面的线连，此连线与盾构推进方向的夹角称为超前影响角，如图3中角β。

3.2 三、四、五维空间中地表沉降几何特性

在三维空间中，地表沉降最终形态是一个“中间深，两侧浅”的沉降槽。

在四维空间中，地表沉降具有了随着步长演化的特征，即不仅是地表沉降槽本身的几何特征，地表沉降槽还随着步长的逐渐推进而不断发展演化。因此，将地表沉降在“四维”空间下的表现形式定义为“沉降超体”，其几何意义为：将地表沉降槽三维图形抽象为一个点(可视为点)，该点沿步长轴而发展演化，表现为“步长-沉降点”的矢量效应。

在四维空间的基础上引入时间变量，不仅能够认识地表沉降槽随盾构施工步长的演化规律，也能得到沉降槽在随步长演化的基础上进一步随着时间的演化规律，即在时间轴上的生长规律，将地表沉降在“五维”空间中的表现形式定义为“沉降卷超体” ，其几何意义为：将地表沉降超体“步长-沉降点”矢量效应抽象为一个点，视该 “点”在沿时间轴发展演化，表现为“时间-步长沉降点”矢量效应。盾构隧道施工引起地表沉降的“沉降超体”“沉降卷超体”等概念的提出，为研究地表沉降的“五维”空间效应提供了新的思路。各维度地表沉降几何特征及属性如表1所示。

表1 地表沉降各维度空间下几何特征、演化规律比较

4 沉降“五维”空间效应工程验证

深圳市城市轨道交通13号线三工区留仙洞站—白芒站区间工程全长4.4 km，盾构机施工过程中地表沉降，现场布设大量地表沉降监测点，用以观测地表实时沉降数据，讨论并验证地表沉降的“五维”空间效应，取监测点1—4说明本文的沉降时间效应，监测点的布置如图8所示。

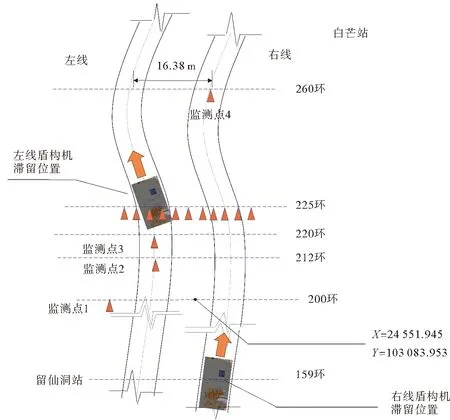
图8 留仙洞站—白芒站区间部分地表沉降测点示意

在深圳城市轨道交通13号线的现场施工过程中，留仙洞站至白芒站区间8月11日至8月13日因现场施工原因并未进行推进。左线盾构隧道滞留于225环，右线盾构隧道滞留于159环。3 d内地表沉降情况(图9)能够准确地反应地表沉降的时间效应问题。

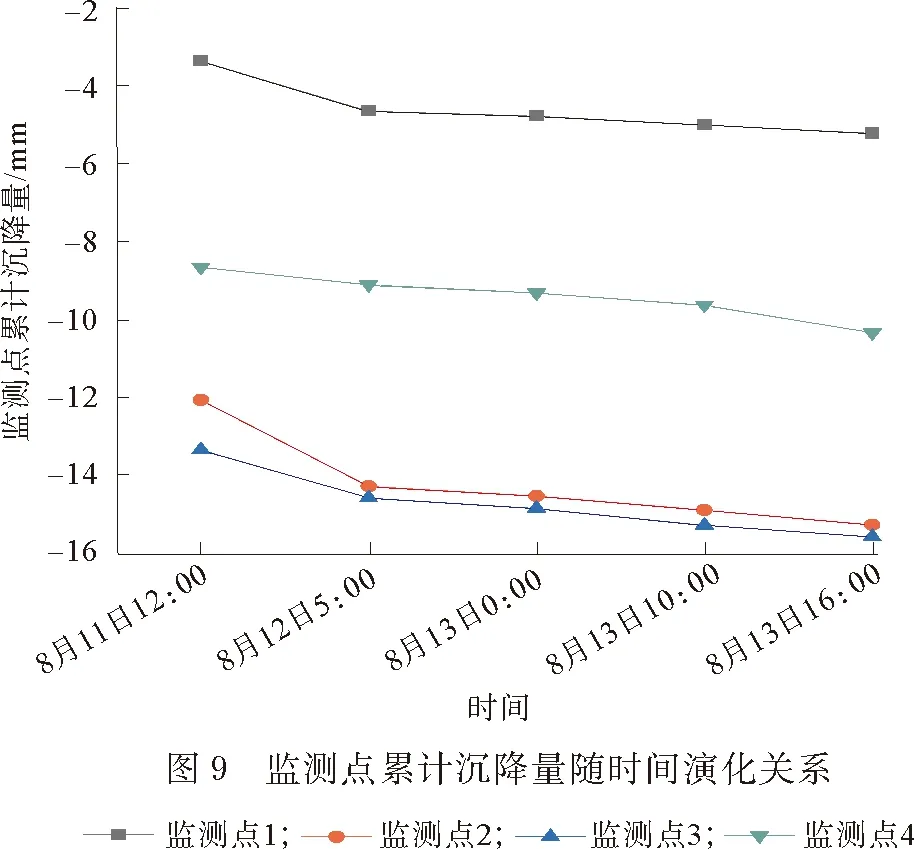
如图9所示，地表沉降的发展过程具有明显的时间效应。在左右线隧道盾构机停机状态下，监测点1—4均发生单独于时间坐标轴上的沉降现象，即地表的沉降过程在不受盾构机推进扰动的情况下，仅随时间的发展而发生沉降。位于隧道中心线上的监测点2和监测点3的地表沉降量较大，而对于偏离隧道中心线上的监测点1所观测到的地表沉降量较小(符合地表沉降的三维空间分布形态)。在盾构机尚未推进至260环时，监测点4因超前影响的原因，也发生了随时间的沉降。

观测左线盾构机从201环推进至222环，监测点2(位于212环)的整个沉降过程。监测点2位于观测区间的中间位置，能够准确反映盾构机未到时、下穿时、穿过时整个周期的地表沉降随盾构机推进步长的演化规律，如图10、图11所示。

由图10可以发现，地表的沉降数据随步长有明显的变化，沉降的步长效应显而易见。在盾构机离监测点2较远时，监测点2因超前影响的原因，发生地表沉降，当盾构机离监测点距离较近时，在盾构机的推力作用下，反而使监测点2出现隆起，当盾构机推过监测点2时，地表继续沉降。在图11中可以直观地看出不同环区间地表沉降和隆起现象，且发现在盾构机靠近监测点时，地表的变形速率最大，离监测点较远时沉降速率较慢。

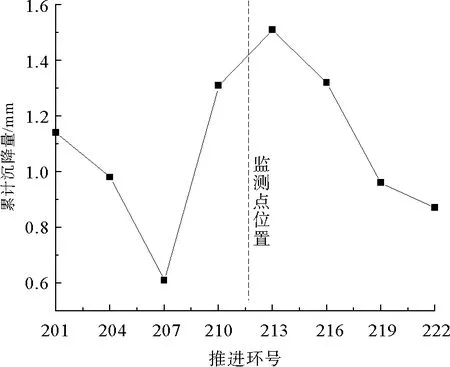
图10 监测点2累计沉降量随盾构机推进环数演化关系

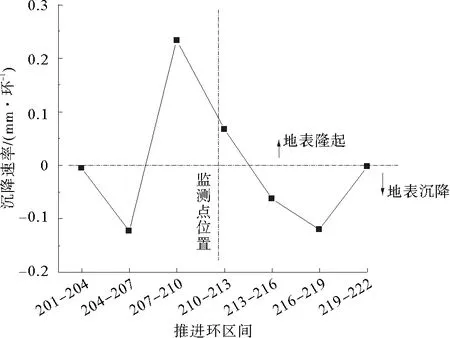
图11 监测点2沉降速率随盾构机推进环数关系

综上，由深圳市城市轨道交通13号线具体监测数据可以得出，地表沉降的发展规律具有明显的时间效应，地表三维沉降槽不但具有步长轴上独立的演化规律，而且也存在时间轴上独立的演化规律，因此地表沉降具有典型的“五维”空间效应得以证实。

5 盾构隧道施工引起地表沉降的“五维”研究展望

盾构隧道施工引起地表沉降“五维”空间效应是个全新的理念，仍有诸多问题需要进一步研究：

1) 在盾构隧道施工引起地表沉降的力学根源上，岩土体的自重可谓是“力源”，盾构隧道施工引起上覆岩土体的自重应力重新分布，在这个过程中岩土体将产生变形，这种变形是地表产生沉降的根源。因此，如何在五维空间中认识隧道上覆岩土体应力重新分布的状态，并研究其变形规律，建立基于五维空间的隧道施工引起地表沉降的力学模型，乃是今后该专题研究的首要任务。

2) 在盾构隧道施工引起地表沉降数学计算模型建立上，盾构隧道施工在地下产生“临空体”，临空体向上发展的过程恰是被扰动的岩土体中空隙演化过程，可谓是“空隙元”，研究盾构隧道施工造成岩土体空隙元在五维空间中的扩散规律，并用微分方程加以描述，从而建立地表沉降的数学表达式，对地表沉降的“五维”效应进行数学计算。因此建立基于“五维”空间的盾构隧道施工引起地表沉降计算模型，也是该专题进一步研究的方向之一。

3) 在工程中，具体研究地表沉降的“五维”空间效应与地质条件参数、隧道几何参数、隧道掘进参数等的具体关系，进一步验证基于“五维”空间的盾构隧道施工引起地表沉降计算模型，并在现场实施可靠的监测予以验证，同时编制基于“五维”空间的盾构隧道施工引起地表沉降预计方法，以求更加深入认识和研究盾构隧道施工引起地表沉降的复杂性和真实过程，并能对工程中的地表沉降现象进行精准(空间上、时间上)的预测。

4) 在盾构隧道施工引起地表沉降多维空间的表示方法上，将张量分析、画法几何等应用于隧道施工引起地表沉降的五维空间效应研究中。地表点的位移是一个时刻指向隧道开挖工作面的“位移矢量”，由单个点的位移矢量到多个点位移矢量组成的三维沉降槽、再到四维的“沉降超体”、五维的“沉降卷超体”，实则是矢量图形的变化过程，用恰当的数学手段和数学工具进行科学描绘，不仅对理解地表沉降多维演化规律具有重要作用，还会有助于理解地表沉降“五维”空间效应的物理机制，在后续研究中可以通过空间矢量运算或张量分析等数学工具，研究沉降槽的“五维”空间效应。

5) 在盾构隧道施工引起地表沉降五维空间的研究技巧上，“降维”的思想方法是研究高维空间的有力手段。对于地表沉降槽的“五维”空间效应研究，运用“降维”的手段可以使复杂多维度的地表沉降演化问题分析更加方便、直观。任何一级低维度空间都是高一级维度空间的横截面，并以高一级维度空间以多出的维度为轴线移动而形成的空间，例如二维空间下的地表沉降线就是三维空间下的地表沉降槽的剖面线，对于“四维”空间下的地表沉降超体，具体来说即是研究三维的沉降槽在步长轴的独立变形规律，同理类比至“五维”空间，将“五维”空间沉降卷超体降维即为沉降超体(三维沉降槽+步长)，研究沉降超体在时间轴上的独立变形规律，即可得到地表沉降的“五维”空间效应。因此，在研究盾构隧道施工引起地表沉降“五维”空间效应时，也可以借用“降维”分析的思想方法，这种“降维”的思想可以使得我们在研究高维问题时寻找到有力的突破点。如图12所示，为地表沉降“五维”空间效应的研究方法。

图12 地表沉降“高维空间”研究方法

6) 与隧道施工引起地表沉降已有经验公式的衔接上，Peck公式、随机介质理论(概率积分方法)在五维空间中的发展；

7) 在实验室研究方面，构建“五维”空间的盾构隧道施工引起地表沉降相似材料模拟实验模型，并进行相应的科学试验验证；

8) 在盾构隧道施工引起地表沉降的多维性研究上，随着人们对科学真谛的追求，对自然或科学中分维、多维的研究兴趣越来越浓厚，坚信盾构隧道施工引起地表沉降的多维性，包括地表沉降的“分维性”“五维效应”是真实存在的，那么如何在更精细的维度(分维)和更高级的维度(五维)上研究地铁隧道施工引起地表沉降的特征和规律，进而在多维度空间建立地铁隧道施工引起地表沉降的“空间-步长-时间演化理论”，乃是该专题今后研究的重要任务。

6 结束语

本文通过对盾构隧道施工引起地表沉降多维性的探索和深圳轨道交通13号线的长期跟踪监测，研究分析了三维地表沉降槽在步长轴和时间轴上的独立演化特征和规律，证明了盾构隧道施工引起地表沉降“五维”空间效应的客观存在性，盾构隧道施工引起的地表沉降具有典型的“五维”空间效应，具体表现为：“三维沉降槽”具有在步长轴上独立的演化的特征，即“三维沉降槽”随步长的推进而发生演化，形成“沉降超体”；而“沉降超体”又在时间轴上独立演化，随时间的增长而发生演化，即形成“沉降卷超体”。

然而，盾构隧道施工引起地表沉降“五维”空间效应是个全新的理念，仍有盾构隧道施工引起地表沉降“五维”空间效应的表示方法、力学机理、计算模型、预计方法等诸多问题需要进一步研究，本文只是抛砖引玉，今后将结合地铁隧道建设项目具体实践进行更加深入的研究。

致谢：感谢导师谢和平院士、张玉卓院士、Marek. KWASNIEWSKI教授、杨伦教授在学术思想上给予启迪，感谢M. D. KOVALENKO教授和I. V. MENSHOVA研究员给予该问题研究的力学和数学启发，张春会教授及李刚、李冉、张永义、朱向飞、张琳、师启蒙等同学多次参加研讨和搜集资料，在此一并表示感谢。