优化耦合模和耦合功率理论在弱耦合扰动多芯光纤中的对比

符小东，潘洪峰，房洪莲，向练

（1 苏州大学 电子信息学院，江苏 苏州 215006）

（2 中天通信技术有限公司，江苏 南通 226000）

（3 中天宽带技术有限公司，江苏 南通 226463）

0 引言

光纤自1966年诞生，经过四十多年的发展，已成为世界信息交互的基石。从单模光纤到多模光纤，从单波长到多波长光纤，光纤通信的发展在稳步前进。然而随着云计算、物联网、大数据等技术的发展，人们对于通信网络的容量要求也越来越高，常规的单模单芯光纤在时间、频率、波长、偏振等物理维度的充分利用，已逐渐逼近非线性香农理论的传输极限值100 Tbit/s［1］。现如今信息获取方式呈现爆炸式的增加，预计在不久的将来将会出现容量紧缩问题。为了超越香农极限容量的限制，达到更高的流量数据吞吐量，研究的重点只能转移到还没有被利用的维度，即空间维度。从物理上讲，增加并充分利用空间维度是进一步提高光纤容量的唯一手段。将空分复用技术应用在光纤中，主要有三种方式：多芯光纤（Multi-core Fiber，MCF）、少模光纤和少模多芯光纤［2-4］。MCF 具有良好的应用前景，如今也慢慢发展起来，但在有限的包层空间内放入多根纤芯，导致各纤芯之间距离很小，使得传输在纤芯的光信号会对相邻其他纤芯造成影响，相邻纤芯之间会产生模式耦合现象，出现芯间串扰（Inter-core Crosstalk，ICXT），影响光纤通信的质量。因此，研究MCF 过程中，如何抑制相邻纤芯的串扰是一个值得关注的问题。

对弱耦合MCF 串扰的研究大多数都是基于耦合模理论（Coupled Mode Theory，CMT）和耦合功率理论（Coupled Power Theory，CPT）［5-10］。基于CMT，HAYASHI T 等［5］提出了匀质弱耦合MCF 中ICXT 纵向演化的离散变化模型（Discrete Changes Model，DCM），该模型包含弯曲和扭转扰动影响。利用DCM 进行串扰估计与实验吻合较好，因此可以作为一种典型的ICXT 估计模型，但由于该模型不适用于非相位匹配区以及异质MCF 中，而实际的MCF，由于生产设备的误差，其纤芯参数并不完全相同，因此DCM 的准确性会受到严重影响。LI Mingjun 等［6］利用CMT 推导了匀质和异质双芯光纤的一般串扰公式，但在实际中，MCF 并不是完全均匀的，不同纤芯的参数略有不同，并且其方程忽略了弯曲和扭转扰动影响，因此是不符合实际的。LIN Gan 等［7］提出一种优化后的数值解法，通过结合四阶龙格库塔法和辛普森积分法来直接求解修正的耦合模方程，然而数值解法耗时较长，不能得出统一的串扰解析式。在实际铺设及使用过程中，光纤会存在弯曲和应力起伏而引起的不规则性，在这种情况下，MARCUSE D［8］提出多模光纤的耦合功率理论，但该理论未考虑光纤弯曲和扭转影响的局部耦合情况，仅考虑了平均串扰。针对上述存在的问题，针对CMT 和CPT 两种理论的基础上，需要提出改进的方法。

本文从耦合模理论入手，对原有的耦合模理论加入光纤弯曲和扭转的影响，并采用分段法推导出光信号功率和串扰的解析表达式，将此模型称为优化耦合模理论模型（Optimized Coupled Mode theoretical Model，OCMM）。在此基础上由耦合模理论引出耦合功率理论，并对耦合功率理论进行优化，得到优化的功率耦合系数，并得出光信号串扰解析表达式，将此模型称为优化耦合功率理论模型（Optimized Coupled Power theoretical Model，OCPM）。最后对比OCMM 和OCPM，对两种模型进行仿真验证。

1 基于耦合模理论的串扰估计

在多芯光纤中，当两个波导之间距离相互接近时，波导之间会发生相互作用，我们将这种现象称为波导间的耦合作用。在弱耦合多芯光纤中，可以忽略纤芯间自耦合，因此在平行多芯光纤中耦合模方程可以表示为

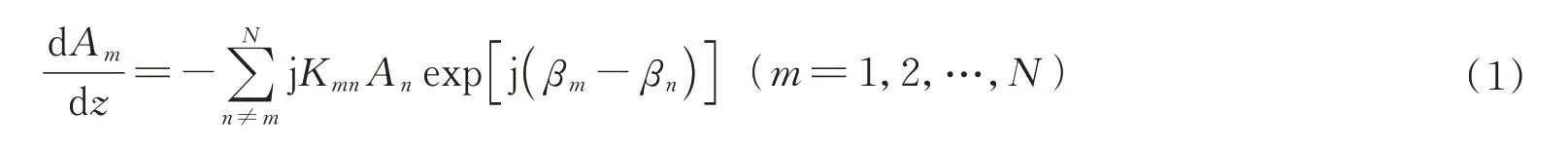
式中，A为电场的慢变复振幅，N为纤芯数量，Kmn为从纤芯n到纤芯m的模式耦合系数，βm和βn分别为m和n芯的传播常数。在无扰平行多芯光纤下，纤芯间的功率耦合呈正弦式振荡分布，如图1 所示为双芯光纤之间在不同情况下的功率耦合情况，其耦合量大小和两个纤芯的传播常数有关。图1（a）是在传播常数完全相同情况下，功率完全耦合转化，图1（b）是在传播常数有微小偏差情况下的功率转化情况。

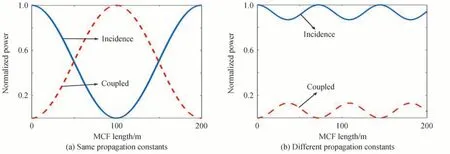
图1 纤芯间功率耦合转换图Fig.1 Power coupling conversion diagram between cores

然而实际光纤在传输时，由于光纤的弯曲和应力起伏的影响，会对光纤传输存在扰动。需要对式（1）耦合模方程进行优化。在存在光纤弯曲和扭转的情况下，假设这两个模式耦合系数沿纵向演化时传播常数不同。因此，在传播常数受光纤弯曲和扭曲扰动的线性传播区域内MCF 的修正耦合模态方程为［11-12］

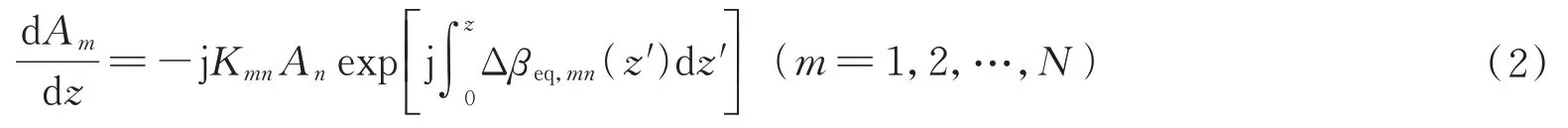
式中，z为传输距离，Δβeq，mn(z′)为在宏观弯曲和扭转结构波动下的纤芯m和n的等效相位失配，可以表示为

式中，βeq，m(z)和βeq，n(z)是纤芯m和n的等效传播常数，其与光纤的弯曲和扭转有关，可以表示为［13］

式中，βc为光纤芯的无扰动传播常数，Rb为弯曲半径，其弯曲方向可为三维空间的任意方向。(r，θ)为弯曲径向方向为θ=0 的MCF 截面上的局部极坐标，表示为θ(z)=φz+ϕ，其中φ和ϕ分别为扭转度和扭转偏移量。光纤的弯曲和扭转示意图如图2 所示。

图2 七芯光纤弯曲和扭转原理图Fig.2 Schematic diagram of bending and torsion of seven core optical fiber

为了推导出真实均匀MCF 中ICXT 的纵向演化的一般模型，采用沿纵向演化的随机相移。为了简化式（2）修正耦合模方程中的积分项，选择将光纤分成N个等长、不相关的均匀段d，其双芯光纤等效原理如图3所示。当分段段长d足够小时，纤芯的等效传播常数在该段内可看作为一个常数，因此式（2）中纤芯间的等效相位失配Δβeq，mn(z)也可简化为一个常数［14］。因此，对于m和n两根纤芯，第i段中的修正耦合模态方程可简化为

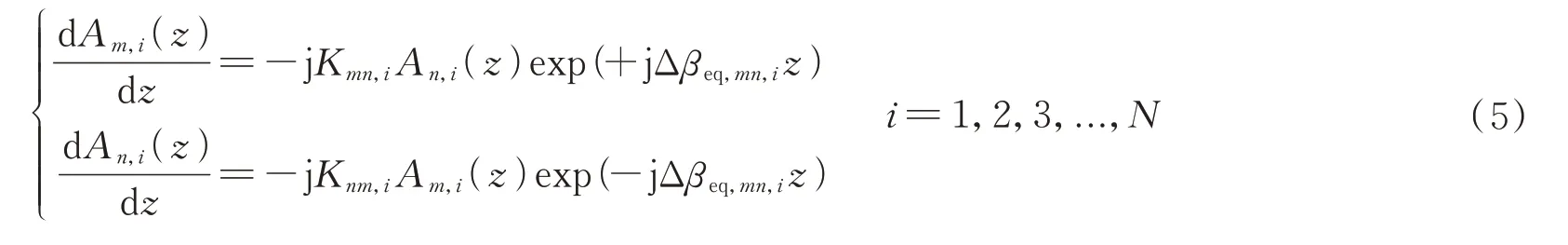
图3 段长为d 的双芯光纤模式耦合原理图Fig.3 Schematic diagram of mode coupling of dual core fiber with segment length d

假设第i-1 段为第i段初始入射功率时，由式（5）可得到解析解的矩阵式为

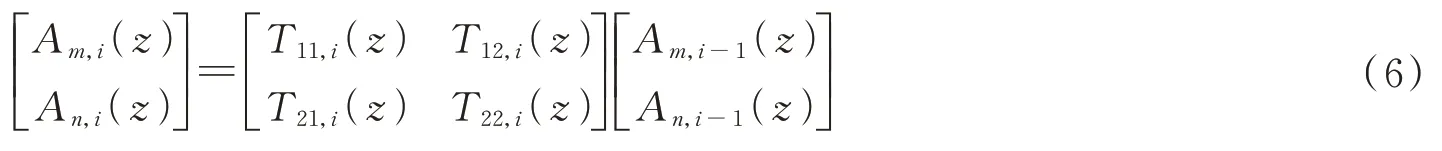
式中，

式中，gi=假设初始时从纤芯m注入归一化功率，n芯为干涉纤芯，在弱耦合条件下，每一段干涉纤芯n的耦合功率可以忽略，纤芯m功率保持为1，在这种情况下，式（6）变为

由功率计算表达式P=|A(z)|2和式（7）、（8）可知，第i段两个纤芯的归一化功率可以表示为

由上述理论模型可知，在弱耦合条件下，在纤芯的N个段长中，激励纤芯的功率可以近似看成1，最终的ICXT 由每一段的串扰的叠加。由串扰的定义可得N段纤芯累加的ICXT 为

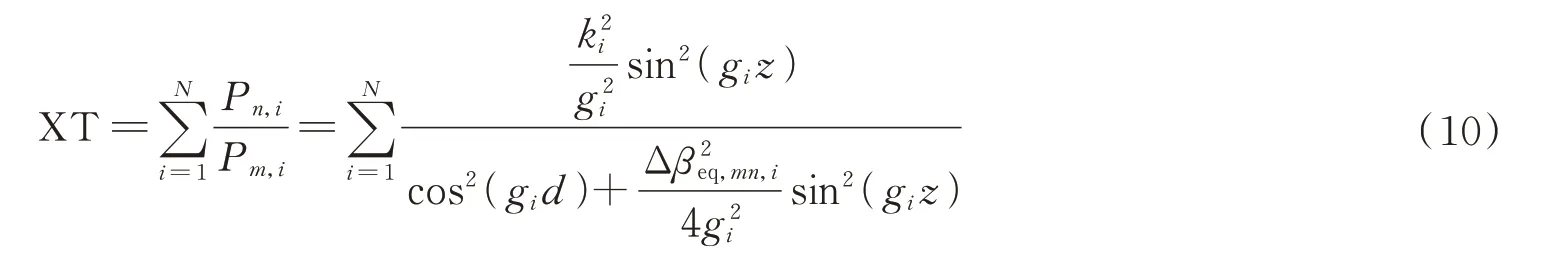
2 基于优化耦合功率理论的串扰估计

在CMT 中，各个纤芯中光功率沿z方向不断进行波动性的相互耦合。然而，当光纤实际长度超过几十米后，由于实际铺设及使用过程中弯曲和应力起伏引起的不规则性，使得光纤耦合不再呈现这种波动性［8］。在这种情况下，CPT 更加有效和精确。

考虑到实际使用过程中弯曲和应力起伏引起的不规则性，由式（1）可知，重新定义的耦合模方程组可以写为［8］

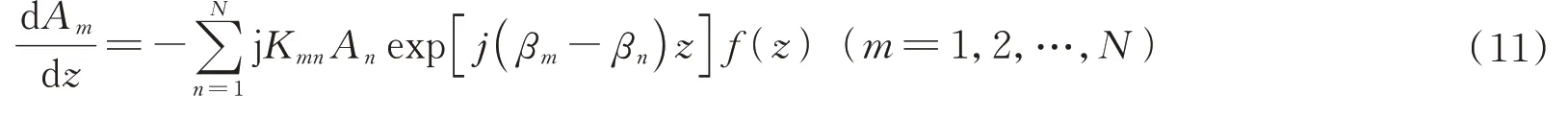
式中，f(z)是描述实际弯曲（弯曲半径为Rb）和扭转效应（扭转率为φ）的相位函数。串扰采用指数自相关函数模拟，经过一系列推导可得耦合功率方程为［8］

式（12）即为功率耦合方程。令

hmn为光波导m和n之间的功率耦合系数。假设在双芯光纤情况下，从纤芯m注入归一化功率，n芯为干涉纤芯，求解式（12）并由串扰定义式XT=Pn(z)/Pm(z)可得，两个纤芯之间的串扰为

由上述可知，推导耦合功率方程的起点是重新定义的耦合模方程。然而式（12）耦合功率方程只能体现平均功率耦合情况，在实际光纤传输中，想要了解光纤纵向的变化，即局部耦合功率方程，需要对耦合功率理论加以修改，在耦合模方程的相位信息中加入弯曲和扭转的影响。因此对于式（11）中的传播常数βm，在z=z′时定义本地等效传播常数为［15］

式中，xm和ym分别为m芯中点在z=0（初始状态）处的x坐标和y坐标，βm为纤芯未受扰动的传播常数，Rb为弯曲半径，φ为扭转率。同样和类似。因此等效传播常数差为

式中，

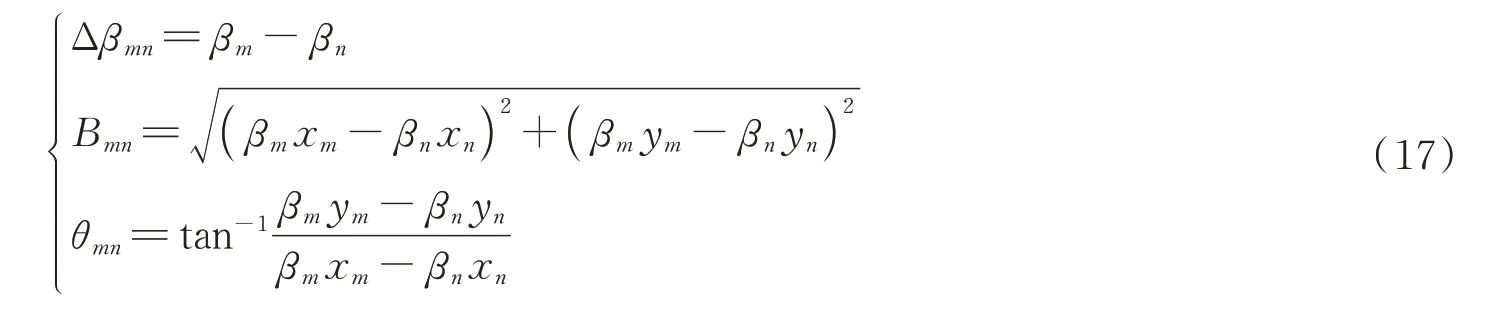
因此优化后的功率耦合系数h′mn为

式（18）与式（13）基本一样，唯一区别就是式（18）中等效传播常数差Δβ′mn包含弯曲和扭转的扰动信息，而式（13）中传播常数不包含扰动信息。为了避免耦合功率方程的数值解，功率耦合系数h′mn在扭转率φ上平均值为［16］

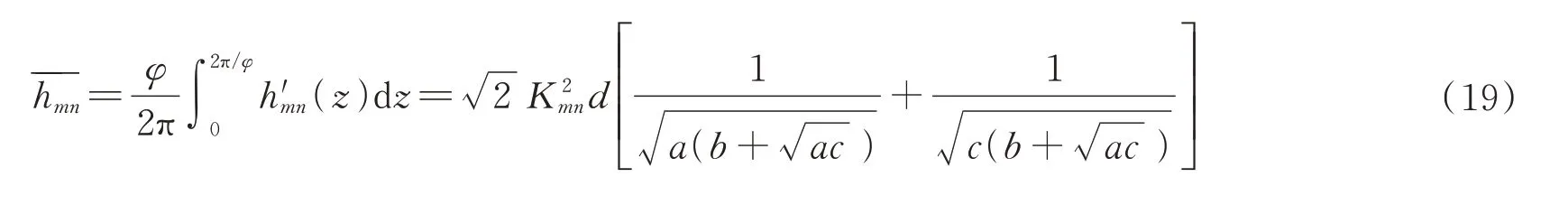
式中，

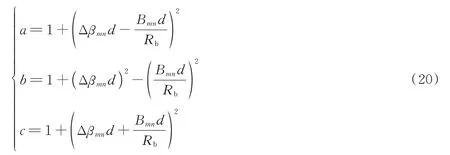
根据式（12）耦合功率方程及式（19）优化后的平均耦合功率系数求解得到ICXT 为

3 仿真对比

上述推导了基于OCMM 和OCPM 的多芯光纤串扰计算方程，本节通过仿真与DCM 模型［5］和参考实验数据［17］进行比较，来验证上述串扰计算的精度。表1 总结了阶跃型七芯MCF 的参数。

表1 阶跃型七芯MCF 的主要参数Table 1 Main parameters of step seven core MCF

在匀质MCF 中，假设芯m和芯n的本征有效折射率为一样的。DCM 在纤芯完全匀质条件下是可靠的，因此将OCMM 和OCPM 的串扰估算与其比较。图4 所示为MCF 在三种模型下串扰随距离的变化情况。串扰随着MCF 长度的增加而增加，呈线性上升趋势，可以看出串扰是不断积累的。图4 左侧可以看出，OCMM 与OCPM 的仿真结果与DCM 和实验结果［17］非常吻合，其中OCPM 与DCM 结果几近重合，且随着光纤传输距离增加呈线性平稳上升趋势。与OCPM 不一样的是，OCMM 是随着DCM 波形呈震荡上升，这是由于在相位匹配点附近，串扰累积增加，在非相位匹配点附近，串扰几乎不变，因此OCMM 可以更好地反应光纤物理结构的波动情况。

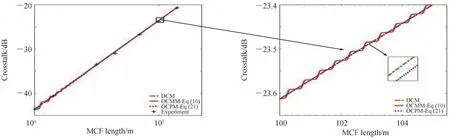
图4 ICXT 随MCF 长度变化关系Fig.4 ICXT as a function of the MCF length

图5（a）、5（b）显示了DCM、OCMM 和OCPM 在实际匀质和实际非匀质MCF 中ICXT 随弯曲半径的变化关系，光纤长度为200 m，其中实际匀质MCF 指的是实际光纤生产的匀质多芯光纤，但由于生产过程的误差会导致纤芯的本征折射率有略微的偏差，而实际非匀质MCF 指的是异质型多芯光纤。从文献［18］［19］可以总结得出，若相邻纤芯之间的本征有效折射率之差（）大于等于0.046 %，我们将该多芯光纤称为异质多芯光纤。如图5 所示，对于非完全同质多芯光纤，存在一个弯曲半径使平均功率耦合系数达到最大值，因此通常将该点定义为临界弯曲半径，用Rpk表示。当=0.012% 和0.020% 时，为实际匀质MCF，其临界弯曲半径分别为Rpk1=250 mm 和150 mm。当=0.046%和0.092%时，为实际非匀质MCF，其临界弯曲半径分别为Rpk1=65 mm 和33 mm。如图5 所示，在实际匀质和实际非匀质MCF 中，在相位匹配区（临界弯曲半径左侧区域）时，其串扰随弯曲半径增大而增大，在非相位匹配区（临界弯曲半径右侧区域），其串扰会随着弯曲半径增大而减小，直至收敛到一个固定值，这是由于传播常数的失配引起相位匹配点数量的减小。由于DCM 仅适用于完全同质多芯光纤中，当相邻纤芯传播常数不同时，DCM 已不再适用于大弯曲半径多芯光纤。由图5（a）所示，在临界弯曲半径左侧，OCMM 和OCPM 仿真结果比较吻合，在临界弯曲半径右侧，OCMM 和OCPM 趋势很吻合，但是由于OCPM 是模拟的平均串扰情况，因此与OCMM略有偏差，在实际匀质MCF 中使用OCMM 更加精确。从图5（b）中可以看出，在非相位匹配区，OCPM 的变化是一个均匀降低的趋势，而OCMM 随弯曲半径变化在OCPM 曲线上是一个震荡降低的过程，但偏差很小。这是由于OCMM 的串扰估计是在实时扰动情况下进行的，而OCPM 是对取得平均扰动进行串扰估算的。因此在实际非匀质MCF 中使用OCMM 或者OCPM 都可以。但是OCMM 的串扰计算式（10）是根据每一段的串扰叠加得出来的，计算复杂度较高，计算速度较慢，而OCPM 的串扰计算式（21）只需要代入光纤参数进去就可以直接计算出，因此计算速度会更快。在两种模型结果相似的情况下，因此选择OCPM 更好一点。

图5 在实际匀质和实际非匀质MCF 中ICXT 与弯曲半径的关系Fig.5 ICXT as a function of the bending radius in actual homogeneous and actual heterogeneous MCF

4 结论

基于OCMM 和OCPM 两种理论模型，针对实际多芯光纤铺设场景下存在弯曲和扭转扰动的情况，研究了多芯光纤的芯间串扰的分布特性，分别推导出芯间串扰的解析表达式。通过与离散变化模型仿真验证对比，验证了理论模型的精度和正确性。仿真结果表明，在同质MCF 中，OCMM 和OCPM 与DCM 结果以及实验结果非常吻合，串扰随光纤传输距离的增大而增大，验证了模型的正确性。实际MCF 中，OCMM 和OCPM 吻合很好。在相位匹配区，串扰随弯曲半径的增大而增大；在非相位匹配区，串扰随弯曲半径增大而减小。在实际匀质MCF 的非相位匹配区，OCPM 与OCMM 仿真结果会有些偏差，这是由于OCPM 是模拟的平均串扰情况，因此在这种情况下OCMM 更精确。而在实际非匀质MCF 的非相位匹配区，OCPM 与OCMM 仿真结果吻合很好，在这种情况下用OCPM 计算速度会更快。此外由仿真图可以看出，OCMM 更能体现光纤实时传输时串扰随扰动波动的情况，但是计算相对较慢；而OCPM 取平均扰动来计算串扰，得出具体解析表达式，计算速度更快，但不能体现实时光纤传输情况。因此可以根据实际情况采用合适的理论模型。