基于双曲初始相位的GS改进算法
修龙汪,李文青,杨鹏,王博伟,张航
(浙江工业大学理学院光电子智能化技术研究所,杭州 310023)
0 引言
激光因其高相干性、高亮度、高单色性和高方向性被广泛应用于激光材料加工、激光医疗、激光雷达、半导体激光热处理等领域[1-3]。根据不同领域对光束形态的不同需求,人们研究了多种光束整形方法,如透射光学(掩模和类掩模镜)[4-5]、折射光学(透镜和非球面元件)[6-8]和衍射光学(传播到远场平面或近场平面)[9-11]。衍射光学元件(Diffractive Optical Element,DOE)能够改变激光相位,得到所需光强分布,并且能量利用率高,再加上体积小、重量轻的优点,成为光束整形中的理想选择[12]。目前被普遍采用的DOE 设计算法有:1)基于全局优化的模拟退火算法[13]、遗传算法[14];2)迭代优化算法,如傅里叶变换迭代算法[15];3)几何变换算法[16]。传统模拟退火算法在收敛性方面不足;传统遗传算法全局寻优方面优点突出,但局部寻优较差,且参数选择困难;迭代傅里叶变换算法转换效率高,且可以处理大阵列数据,但对初始相位非常敏感;几何变换算法虽然有很高的输出效率,但光束质量相对较差。采用传统单一算法并不能获得很好的整形结果,于是人们又研究了基于传统优化设计算法的混合算法和基于传统优化设计算法的改进算法。
鲁建业等[17]提出了一种混合遗传-模拟退火算法直接设计二元衍射光学器件的方法,并对高斯基模光束整形为平顶光束的过程进行了模拟计算,数值计算误差小于6%,衍射效率高于93%。庞辉等[18]提出了一种混合遗传迭代爬山算法,获得了很好的整形效果。林勇等[19]提出了一种平滑修正和模糊控制迭代算法,其中平滑修正法有效改善了输出光束的顶部均匀度,却增大了均方根误差值,模糊控制迭代算法降低了均方根误差,能量转换效率为94.91%。李昕颖等[20]提出了一种基于几何映射理论的衍射光学元件优化算法,在迭代过程中加入一个反映衍射效应的参量,通过修正初始相位,有效抑制了散斑和振铃效应,衍射效率达到96.20%。邹杰宇等[21]利用不动点迭代法解非线性方程以加速迭代过程的思想对Gerchberg-Saxton(GS)算法进行了改进,模拟结果表明均方根误差相比传统GS 算法减少了33.05%。庞辉等[22]又使用特殊球面相位轮廓作为初始相位,有效地消除了散斑噪声,但要找到合适的球面相位是不容易的。杨美霞等[23]采用一种精细采样方法来抑制散斑,该方法对部分散斑有良好的抑制效果。TAO S 等[24]提出了双约束GS 算法,即在迭代过程中同时对输出面的振幅和相位进行约束,但该方法的能量集中度降低了1 个数量级。
为了获得高衍射效率低散斑的连续面型DOE,本文提出了一种改进的GS 算法,引入双曲面初始相位形式,先利用迭代寻优算法获得最优初始相位,再通过迭代优化算法获得DOE 相位,最后再通过爬山邻域优化算法,获得最终DOE 相位,得到的DOE 相位还可以通过相位展开算法进行展开,以降低量化引入的加工误差。以方形光斑为例,证明该方法的有效性。
1 设计方法
GS 算法是比较常用的一种迭代算法,但容易受初始相位影响,初始相位的选择很大程度上决定了最终结果的好坏。传统GS 算法原理如图1 所示,首先,用入射光振幅乘以DOE 相位作为输入光场的场分布,DOE 初始相位为随机相位φ,入射振幅为高斯光束;其次,通过衍射变换获得输出面光场分布;再次,用目标振幅乘以输出面光场相位作为新的输出场分布,通过逆衍射变换得到输入面光场分布,然后用新的输入面光场相位φ′乘以入射振幅分布作为输入面光场分布,进行新一轮的正向衍射变换和逆向衍射变换,直到迭代至终止条件;最后,获得最优的DOE 相位分布。衍射变换有菲涅尔衍射变换和夫琅和费衍射变换,实际衍射计算中,通常采用快速傅里叶变换,以提高计算速度。
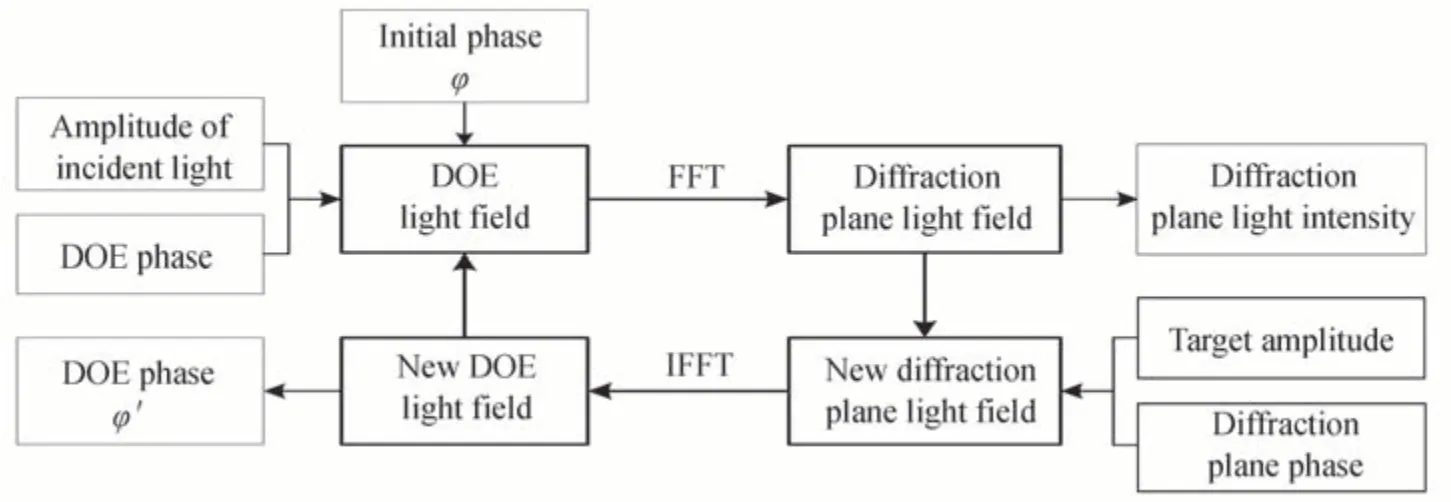
图1 传统GS 算法流程Fig.1 Flow chart of traditional GS algorithm
传统GS 算法因为采用随机相位分布作为初始相位,无法避免在最终的结果中有散斑噪声的存在,为了抑制散斑噪声,引入双曲面初始相位形式φ=d×(x2-y2),不同于已有的初始相位形式,添加相位参数d,通过迭代寻优算法,共同确定初始相位。为了获得更优的DOE 相位和更高的衍射效率,在迭代优化算法后,加入爬山算法进行邻域优化,对提升光斑的质量有很好的作用[18]。为了定量地评价光斑质量,采用衍射效率η和均方根误差(Root Mean Square Error,RMSE)两个指标,定义为
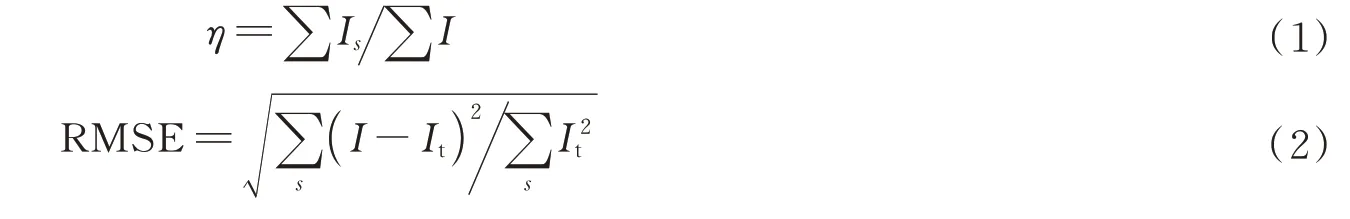
式中,Is为目标区实际光强,I为实际光强,s代表平顶光束所在区域,It为目标光强。
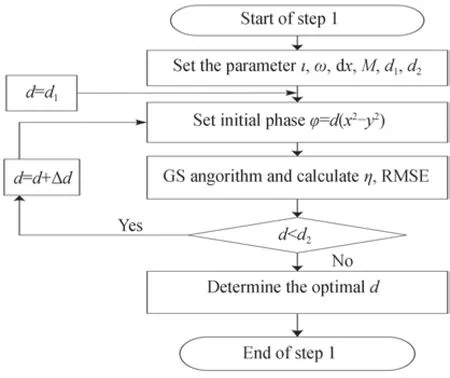
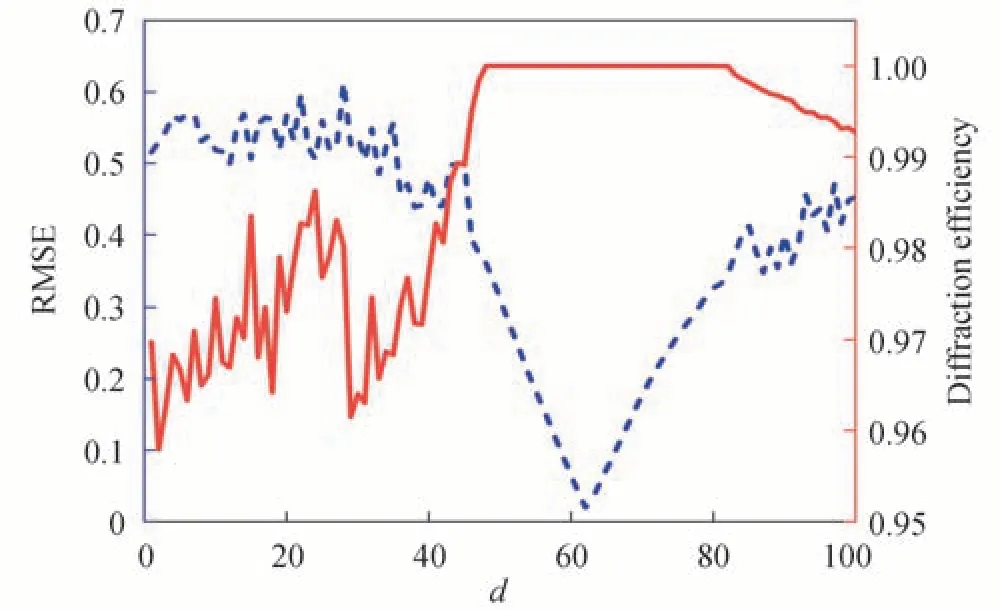
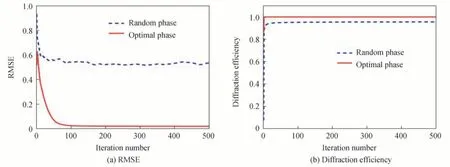
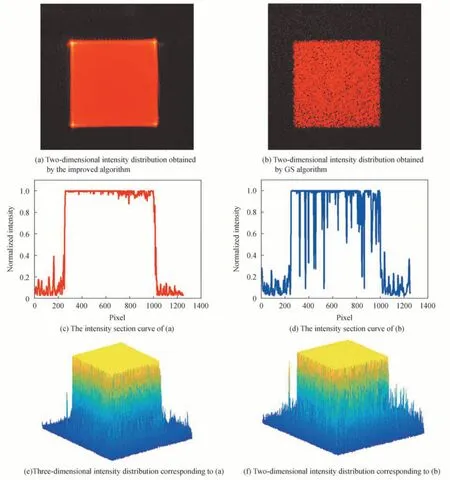
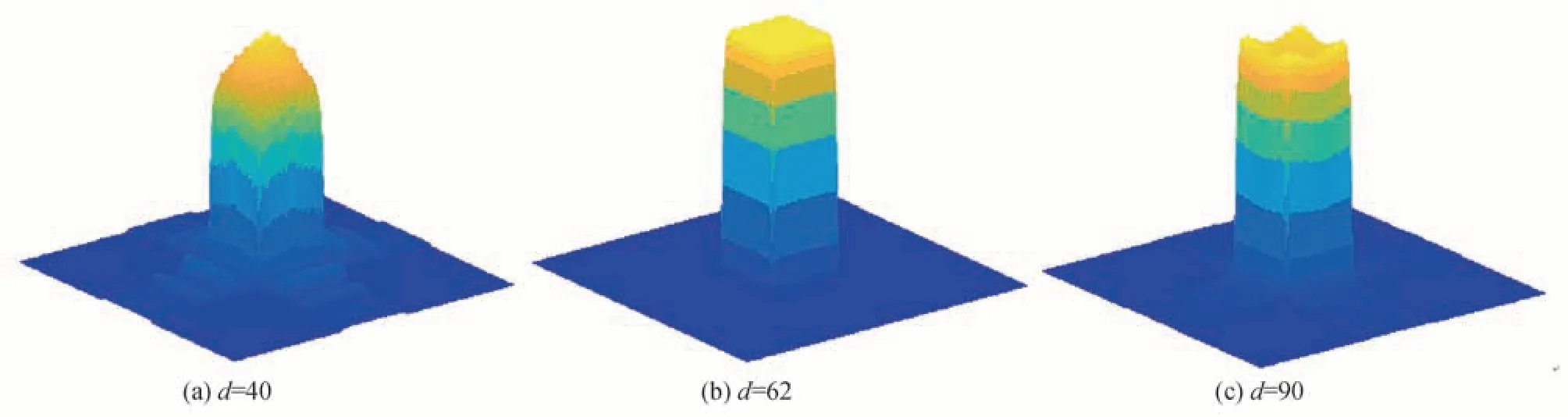
为了获得连续面型衍射器件,在邻域优化算法后加入相位展开算法,展开后的相位,可以通过移动掩模工艺进行加工制造,避免因量化引入加工误差。至此,改进的GS 算法,融入了迭代寻优算法、迭代优化算法、邻域优化算法、相位展开算法,可以获得较为满意的整形结果,算法流程和迭代寻优算法流程如图2、图3所示。给定目标光斑所占像素数ι,高斯光束束腰半径ω,输入面单元尺寸dx,输入面输出面离散点数M×M,相位参数d的上下限,上限d1,下限d2。先令d等于d1,通过传统GS 迭代,获得衍射效率η和均方根误差RMSE,然后判断d 图2 改进的GS 算法流程Fig.2 Improved GS algorithm flow chart 图3 迭代寻优算法流程Fig.3 Flow chart of iterative optimization algorithm 分别用传统GS 算法和改进算法设计DOE,将高斯光束整形成均匀方斑,入射高斯光束振幅可以表示为 目标矩形平顶光束振幅可以表示为 式中,x、y是输入面坐标,ζ、ξ是输出面坐标,w是超高斯光束束腰半径。在仿真模拟计算中,具体参量选择如下:入射光波长λ为632.8 nm,高斯光束束腰半径ω为960 μm,超高斯光束半径w为3.24 mm,目标光斑所占像素数ι为120,输入输出面离散点M×M均为512×512,输入面单元尺寸为8 μm×8 μm,输入面和输出面距离F为350 mm,输出面单元尺寸为54 μm×54 μm,d1=1,d2=100,Δd= 1。图4 为迭代寻优曲线,图5 为采用最优的初始相位φ=62×(x2-y2)进行迭代优化,获得的RMSE 和衍射效率η的变化曲线。 图4 迭代寻优曲线Fig.4 The curve of iterative optimization 图5 均方根误差和衍射效率Fig.5 The RMSE and diffraction efficiency 图4 反映了在迭代寻优算法中,随着相位参量d的变化得到的衍射效率η和RMSE 变化曲线,当相位参量增加时,衍射效率从小变大,在d=48 时,达到最大值,而后趋于稳定,接近于1,在d=83 时,又开始下降;RMSE 随相位参数的增加,先波动下降,当d=45 时,开始以一定趋势下降,当d=62 时,下降到最小值0.020 2,而后开始以一定趋势上升,当d=85 时,又开始波动上升;所以,当d=62 时,为最佳的相位参数。图5 反映了用传统GS 算法和改进算法分别仿真,得到的衍射效率和RMSE 随迭代次数的变化曲线,传统GS 算法最大衍射效率为0.958,RMSE 为0.583,而改进的算法可以达到0.999 的衍射效率;均方根误差为0.018 7。图6(a)是采用改进算法获得的DOE 相位分布,图6(b)和(c)是采用改进算法获得输出面上光强分布和相位分布;可以看出光强被很好地集中到了信号区域,且散斑效应被有效抑制,DOE 相位规则有序,可以通过相位展开算法进行展开,以消除2π 跃迁;图6(d)是采用传统GS 算法获得DOE 相位分布,图6(e)和(f)是采用传统GS 算法获得的输出面上光强分布和相位分布,和改进算法相比,散斑效应明显,且DOE 相位图杂乱无章。 图6 方形平顶光束的仿真结果Fig.6 The simulation results of the square flat-topped beams 图7(a)和(c)反映了通过改进算法获得的DOE 相位展开图和相位展开截线,图7(b)和(d)反映了通过传统GS 算法获得DOE 相位展开图和相位展开截线。显然,采用改进算法获得的DOE 相位展开后,表面平滑且连续,易于通过移动掩模工艺进行加工制造,降低量化引入的加工误差。 图7 相位展开图和相位展开截线Fig.7 Phase unwrapping diagrams and phase unwrapping transversals 为了进一步验证提出的改进方法,进行了光学实验,实验中采用纯相位型的空间光调制器(Spatial Light Modulator,SLM)来显示设计得到的衍射元件的相位分布,这样可以有效避免传统衍射元件加工制备所需的繁杂工艺。SLM 是一种动态相位调制器件,目前已广泛用于光束整形[2,23]、全息显示[25-26]、图像重构[27]等领域。实验光路如图8 所示,波长为632 nm 的氦氖激光经扩束镜后透射到SLM(型号为HOLOEYE PLUTO VIS,分辨率为1 920×1 080,像素大小为8 μm×8 μm)上,利用计算机将设计好的方形平顶光束对应的相位分布输入到SLM 中,调制后的光场再经傅里叶变换透镜透射到焦平面上的CCD(型号为HR16000CTLGEC,像素数为4 896 pixel×3 248 pixel,像素尺寸为7.4 μm×7.4 μm)上,CCD 用来采集焦平面上的光强分布,为了使SLM 处于纯相位调制模式,在光路中加入了偏振片使得入射到SLM 上的激光偏振方向为水平方向。 图8 实验光路Fig.8 Experimental setup 图9(a)、(c)、(e)为利用改进算法得到的方形平顶光束实验结果。作为对比,图9(b)、(d)、(f)是利用传统GS 算法设计得到的方形平顶光束实验结果。由截线曲线看出,利用改进算法得到的方形平顶光斑均匀性显著优于传统GS 算法,且激光散斑明显减少。利用散斑对比度Sc来衡量散斑抑制的程度,即 图9 实验结果Fig.9 Experimental results 式中,σ和分别为信号区内光斑强度的标准差及信号区内光强强度的平均值。经计算,改进算法得到的方形平顶光束散斑对比度为0.011 8,GS 算法得到的散斑对比度为0.231 9。 提出的相位参数d对输出光斑的质量有很大的影响,且存在一个最优值满足高衍射效率和低均方根误差的要求,图10 分别给出了当d等于40、62 和90 时的光斑仿真结果。可以明显的看出,当d=40 时,输出光斑中心有很大凸起;当d=90 时,输出光斑有很大的凹陷;当d=62 时,光斑质量最佳,既无凸起又无凹陷。 图10 相位参数对输出光斑的影响Fig.10 The influence of phase parameters on the output spot 入射高斯光束束腰半径对输出光斑也是一个重要的影响因素,图11 分别给出了束腰半径为650 μm、960 μm 和1 550 μm 情况下的仿真结果。可以清楚地看出,当ω=650 μm 时,输出光斑均匀性有所下降,出现了一些条纹;当ω=1 550 μm 时,输出光斑有明显的条纹,光斑能量大幅下降;当ω=960 μm 时,输出光斑均匀性很好,且能量绝大部分被集中在目标区域。 图11 入射高斯光束束腰半径对输出光斑的影响Fig.11 Influence of incident Gaussian beam waist radius on output spot 入射高斯光束和DOE 之间有一个最佳位置关系,即入射高斯光束的中心要和DOE 的中心对准,如果偏离最佳位置关系,对输出光斑会产生很大的影响,导致光斑质量下降。图12 分别给出了在水平方向两中心偏离−1.024 mm、0 mm 和1.024 mm 三种距离下的仿真情况,规定向右为正方向。从图中明显看出,两者中心偏差导致输出光斑出现条纹,均匀性有一定程度的下降。 图12 入射高斯光束和DOE 中心偏差对输出光斑的影响Fig.12 The effect of incident Gaussian beam and DOE center deviation on the output spot 在实际加工制作中,制造容差是一个不可忽略的重要参数。为此,对优化后的DOE 进行了制造容差敏感度分析。在最终的DOE 相位分布上添加两种随机扰动,分别为0.10π、0.01π,观察衍射面的光斑质量,并与未加扰动的结果进行对比。由图13 可见,在随机扰动0.01π 下衍射光斑未见明显变化,与原光斑几乎无异,即使加上了0.1π 的随机扰动,衍射光斑的形状依然保持良好,仅在内部均匀度上出现一定的下降,目标信号区域出现散斑。 图13 DOE 的制造容差对光斑质量的影响Fig.13 Influence of manufacturing tolerance of DOE on spot quality 综上分析,对高斯光束进行方斑整形时,改进算法所得结果具有衍射效率高、形状更规整和均匀性更高的优点,在衍射效率、均方根误差或散斑对比度等方面相较于文献[20,22,28]所述方法均有一定的提升。 在GS 算法的基础上,本文引入双曲面初始相位形式,添加相位辅助参量,经过迭代寻优算法、迭代优化算法、邻域优化算法获得最终的DOE 相位。利用该算法设计的方形平顶光束在仿真和实验中的性能均优于传统GS 算法和近期类似的GS 优化算法,仿真结果中,改进算法的衍射效率为0.999,均方根误差为0.018 7,实验结果中,散斑对比度为0.011 8。最后,通过相位展开算法将得到的DOE 相位进行了展开,得到了连续面型衍射器件相位,为采用移动掩模工艺加工制造提供了很好的应用场景。 致谢由衷感谢中国科学院光电技术研究所的庞辉副研究员对本文工作的精心指导。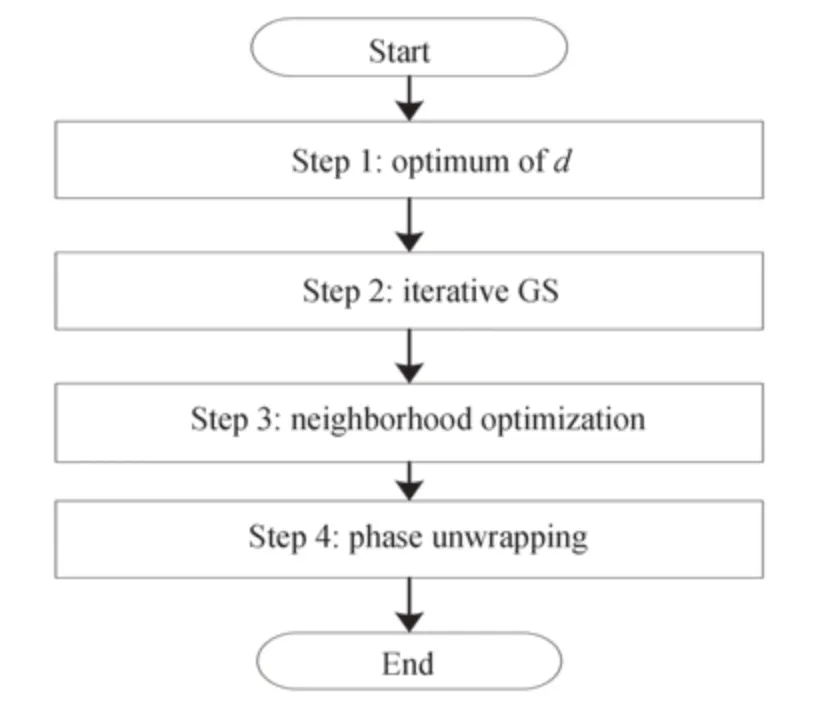
2 仿真




3 实验


4 讨论
4.1 相位参数d 对输出光斑的影响
4.2 束腰半径对输出光斑的影响

4.3 中心偏差对输出光斑的影响

4.4 DOE 优化设计的容差分析

5 结论

