基于补偿距离估计的光纤振动信号特征提取算法
许海燕,寇庆康,谢迎娟,朱俊,李敏
(河海大学物联网工程学院,江苏常州 213022)
0 引言
光纤传感系统广泛用于油气长输管道、隧道安全监测、大型结构安全监测、周边安全等诸多领域[1-5]。光纤传感信号识别在实时监测、异常报警等多个方面起关键作用,其工作性能直接决定了整个监测系统的性能,因此,能否快速、准确地进行识别分类对于保障维护各个领域的安全和减少设备损坏造成的成本损失而言具有重要意义。
经过光纤传感系统提取的特征向量代表了光纤振动信号的特征,提取算法的有效性直接影响事件识别结果的准确性。因此,根据特征提取算法,获得有效的特征参数,对提高识别率尤为关键。国内外学者已经在这方面做出大量研究。LI Junchan 等提出了一种基于相关向量机的光纤振动传感器模式识别方法[6]。首先对初始振动信号进行小波去噪预处理,然后利用小波分解算法得到各级分解系数,构建特征向量,最后利用相关向量机作为分类器进行分类识别。但是基于小波分解的特征提取方法由于信号的特征容易受到高斯噪声的影响,在小波分解处理过程中存在模糊提取和线性稳态的缺陷。WANG Liang 等提出基于门限过零率和稀疏编码器的算法提取光纤振动信号的两级特征[7]。第一级特征提取过零率特征,以识别振动是否发生,通过第一级特征提取,降低光纤振动信号数据的维数。在发生振动的情况下,采用稀疏自编码神经网络算法提取振动信号的高维特征。但是采用神经网络算法需要大量数据进行训练。LIU Kun 等提出并论证了一种基于混合特征提取算法和组合分类器的识别方案[8]。提取过零率、样本熵、小波包能量熵、峰度和多尺度置换熵组合为混合特征向量,然后采用一种支持向量机和径向基函数神经网络相结合的分类器进行识别分类。但是多种特征提取方案会增加特征提取过程的时间成本。
近年来,借鉴听觉感知机理的Mel 频率倒谱系数(Mel-frequency Cepstral Coefficients,MFCC)特征提取方法在振动信号特征提取中得到了广泛的应用,其算法简单,能有效提取出高度可识别的特征信息,并取得良好的分类效果。 MFCC 特征提取方法可以对光纤传感系统采集到的振动信号进行特征提取,进而对模式进行预测,从而识别干扰信号[9]。使用MFCC 特征提取算法时,提取的特征向量存在维数高、向量冗余的问题。当它被送到分类器进行训练和识别时,不仅会增加时间成本,还会降低识别准确率[10]。因此,如何实现对MFCC 特征向量的有效降维是提高光纤传感振动信号实时性和准确性的关键。
目前已知的降维技术分为两类:一类是基于原始特征向量进行选择,另一类是从原始特征中重新提取特征[11]。主成分分析(Principal Component Analysis,PCA)被广泛用于降低MFCC 特征向量的维数。通过从原始特征向量中重新提取特征向量,实现了MFCC 特征向量的特征降维,可以提高识别和分类[12]。但是,由于主成分分析方法是从原始特征向量中重新提取特征矩阵,对原始特征向量的各个特征维度的意义具有一定的模糊性,方差小的非主成分也可能包含不同的信息。对后续的识别和分类会产生一定的影响。
针对上述问题,本文提出了一种基于补偿距离估计技术(Compensation Distance Estimation Technology,CDET)的特征提取方法,采用对特征向量类内离散性和类间离散性联合评估的方式,对特征矩阵的不同维度进行特征评分,通过在原有特征向量矩阵中删减低评分冗余向量进行特征降维,从而解决冗余向量对分类的影响以及特征提取维数过多造成的运算复杂问题。
1 算法原理
本文提出一种基于补偿距离估计的特征提取方法。通过该算法可以解决特征向量维数过多导致的复杂运算问题。基于补偿距离估计的特征提取算法可以优化特征向量矩阵,减少影响分类精度的冗余向量。采用基于听觉感知机理的MFCC 算法进行初次特征提取,并制定特征筛选策略,采用补偿距离估计技术降低特征维数,解决MFCC 提取的特征矩阵维数过多的问题,提高光纤传感信号识别的有效性和实时性。MFCC 特征提取算法流程如下:
输入:{Xc,n|1 ≤c≤C,1 ≤n≤Nc}
输出:{C(n),D(n),D2(n)}


1.1 光纤传感信号MFCC 特征提取
MFCC 特征提取方法是语音识别、故障识别和光纤信号识别中常用的一种特征提取方法[13-15]。 MFCC将信号频率转换为Mel 频率,设置等距Mel 频率,再转换为频率,得到Mel 频率滤波器,然后将每个带通滤波器的输出信号能量作为信号的基本特征[16]。MFCC 特征提取算法的输入为不同类型的光纤振动信号样本,根据算法流程得到MFCC 系数与差分系数组合矩阵的输出。MFCC 向量的三维图如图1。
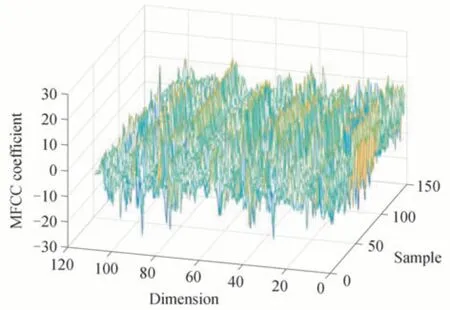
图1 MFCC 三维特征图Fig.1 MFCC 3 dimension feature map
1.2 基于CDET 的特征筛选算法
补偿距离估计技术(CDET)基于特征筛选策略,通过求取特征类别之间的类间距与特征的类内距,根据其比值获得特征评分,去掉评分低的冗余特征维度从而达到降维的目的。详细步骤如下:
设有C个模式类集合为

式中,fc,n,k为第C个模式类下第n个样本第k个特征;Nc为c类模式下的样本总数;K为每个样本特征数目。
在每类模式下,有Nc个样本,因此共有Nc个样本,则有个特征,特征集定义为{fc,n,k}。
补偿距离评估技术实现步骤具体如下:
1)计算相同条件样本的平均距离

平均化dc,k得到平均类内距

2)定义并计算的方差因子

3)计算不同条件样本之间的平均距离

计算不同条件样本之间的平均类间距离
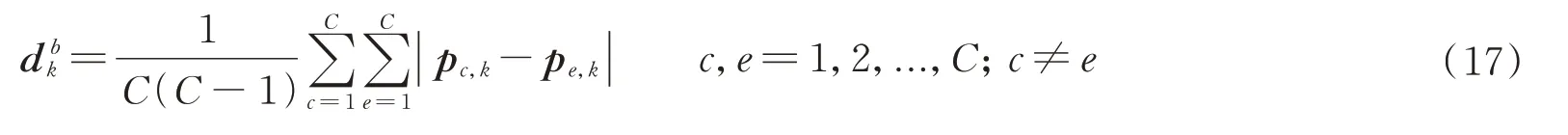
4)定义并计算的方差因子
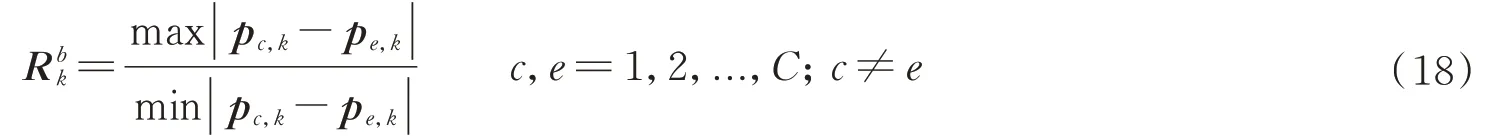
5)定义和计算补偿因子为

6)计算和的比值并乘以补偿因子

将gk归一化,得到距离评价标准

7)设阈值为N,根据评分值确定阈值内的特征数,选择在阈值范围内的L个特征,将k维降至L维。
2 实验结果与分析
2.1 实验数据
实验所用的光纤信号数据来源于实验室光纤传感信号采集系统采集的三种信号种类,分别是晃动、轻敲、重敲,三种信号的时域图如图2。经过预处理与端点检测,将信号分割。实验使用三类信号共210 个样本,每类使用50 个样本,共150 个样本作为训练集;每类使用20 个样本,共60 个样本作为测试集。其中,样本的采样频率为10 kHz。

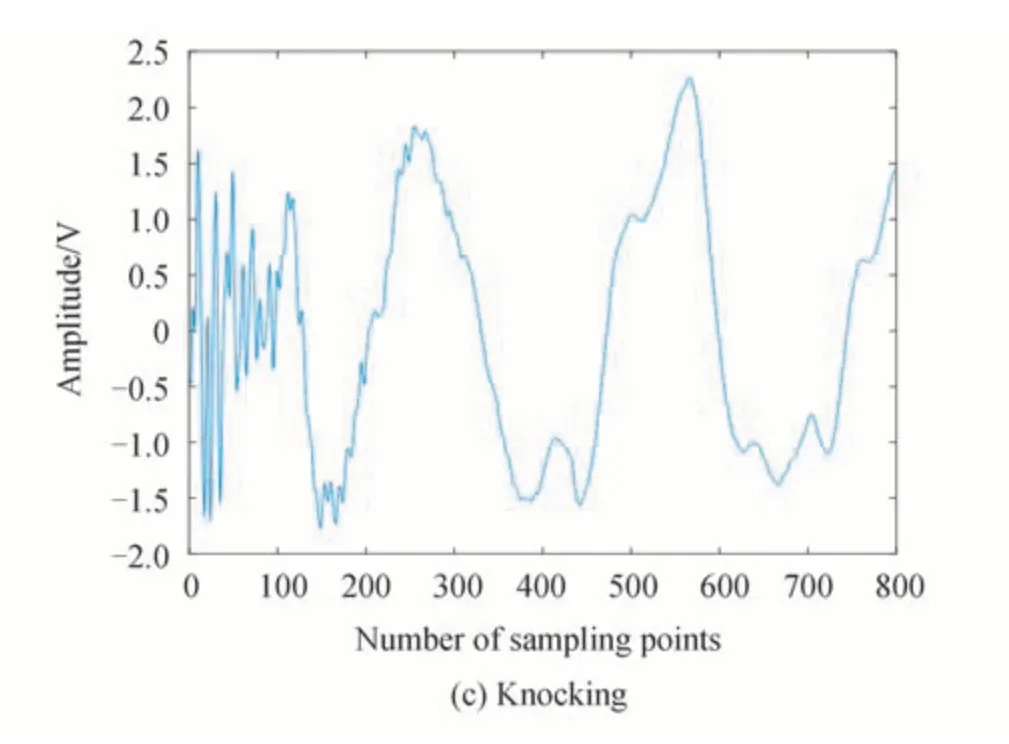
图2 三种信号时域图Fig.2 Time domain diagram of three kinds of signals
2.2 结果与分析
为了验证提出的MFCC 优化方法的有效性,实验中将采用支持向量机(SVM)的方法验证MFCC 特征向量优化前与优化后的整个处理系统对三类信号分类识别的准确率,如表1。经过SVM 的分类准确率结果为与人工标注比较获得。实验流程可描述为3 个步骤:
1)MFCC 特征向量提取:对每个光纤振动信号样本加窗分帧并做FFT,然后将信号变换到Mel 频率刻度下,最后通过倒谱分析得到MFCC 向量。
2)特征降维:特征降维技术主要分为两类,一类是通过选择原有特征向量,删减冗余向量,例如本文所提出的补偿距离估计算法;另一类是通过从现有特征重新提取特征来降低维度,例如作为对比实验方法的主成分分析。
3)SVM 识别分类:将MFCC 特征向量或者经过降维方法处理的特征向量输入训练好的SVM 分类器进行识别,标识结果与识别结果比对,计算正确率并输出。
采用本文提出的对MFCC 向量进行CDET 特征评分算法,评分结果如图3,从图中可以发现1 维、41 维、78 维的评分结果最高,根据评分图可以选择高评分维度,通过删减低评分维度即冗余向量进行特征降维优化。为了便于观察并选择合理降维维度,设置了阈值N,不同阈值下的维度分布如表2,随着阈值的增大,高评分维度相应减少。在SVM 分类实验中对于降维维度的选择根据不同阈值下的特征维度进行分类实验。

图3 CDET 评分表Fig.3 CDET-score chart

表2 不同阈值下特征维度Table 2 Characteristic dimensions at different thresholds
采用SVM 分类器识别三类光纤振动信号的结果如图4。从图4 可以看出,使用CDET 降维到18 维、24维、30 维时,分类效果最好,保留了有用特征向量,对所有冗余向量进行删减,此时的特征评分范围为0.45 到0.55 之间;而PCA 在15 维、18 维、24 维时降维效果最好,根据PCA 的原理符合低纬度时降维分类效果更好的情况。在10 维与15 维时,使用PCA 降维处理的分类效果要优于使用CDET 降维处理的分类效果,因为PCA 是通过对原有特征向量集成产生的新的特征向量,而CDET 是在原有特征向量上选择高评分特征向量,删减冗余向量,当删减过多时,会造成非冗余特征向量的损失。随着特征维数的增加,使用PCA 降维处理的分类效果逐渐下降,甚至低于未经过降维处理的分类效果,而使用CDET 降维处理的分类效果仅仅下降了1.5%,保持稳定。

图4 三类信号不同降维维度下的分类准确率Fig.4 Classification accuracy under different dimensionality reduction dimensions of three kinds of signals
在传统的MFCC 特征提取方法的基础上使用CDET 降维处理,识别正确率与未做优化前相比有所提升,平均识别正确率较传统MFCC 方法提升了3%左右。
对应图4 不同维度下的分类结果,图5 显示了不同维度下的时间成本。计算降维优化时间和分类时间。降维优化的时间成本是直接根据训练样本的CDET 得分图提取特征向量所需的时间,不同维度下的降维优化时间可以保持在0.5 s 左右。没有降维优化的MFCC 特征向量需要2.2 s 才能通过SVM 分类器进行分类。经过降维优化后,SVM 分类器对MFCC 特征向量分类的时间随着维数的增加而增加,总的时间消耗也随着维数的增加而增加。在61 维中,时间成本等于没有降维优化的时间成本。结合不同维度的分类结果和时间成本,在低维度上可以提高分类结果,降低时间成本。

图5 时间消耗曲线Fig.5 Time consumption curve
为了进一步对两种方法做出比较,通过验证不同信噪比下MFCC 特征向量的优化效果比较两种方法的抗噪性能。实验中将高斯白噪声以0 dB、5 dB、10 dB、15 dB、20 dB 的信噪比叠加到三种光纤振动信号中,对SVM 分类器识别正确率进行对比,测量优化方法的抗噪性能。图6 为叠加不同信噪比噪声的CDET 评分图,随着信噪比减小,噪声比例增大,观察评分图可以发现高评分特征向量减少,特征向量的中间评分值增多,表明特征向量辨识度减小。
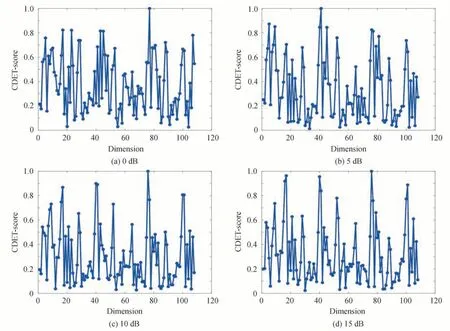
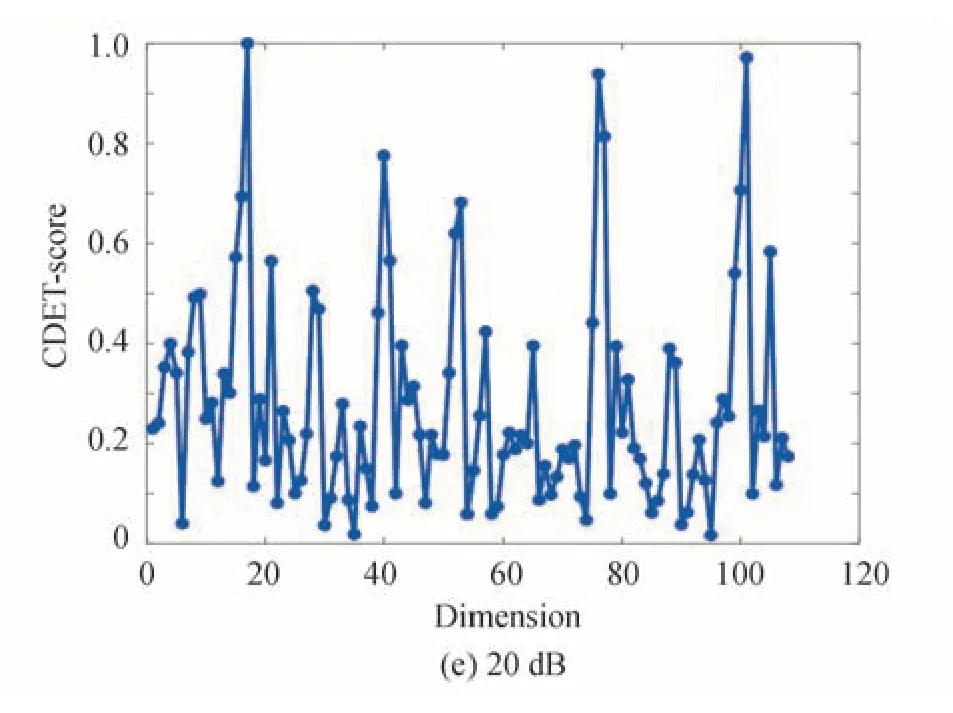
图6 不同信噪比下CDET 评分图Fig.6 CDET-score chart under different signal-to-noise ratio
叠加噪声后测试的分类正确率结果如表3,参考分类实验的实验结果,选择最优分类结果时的维度进行叠加噪声的实验,不同维度的分类准确率与差值结果如图7。从表3 的结果可以发现,在同一信噪比的情况下,随着维数的增多,基于CDET 优化的MFCC 特征向量通过SVM 分类准确率增加,说明在存在噪声的情况下,由于特征辨识度下降,从而需要的特征向量维数增多。从图7 的结果可以看出,随着信噪比的降低,传统MFCC 特征向量在SVM 分类器中的分类结果正确率也随着下降,这是由于噪声的增加掩盖了原有的信号特征;基于PCA 和CDET 降维的MFCC 特征向量在使用SVM 分类时,随着信噪比减小,分类结果正确率虽然也随着下降,但是下降幅度不是很大。从图7 可以发现在相同信噪比下,使用降维处理的特征向量比传统MFCC 特征向量在使用SVM 分类时对于分类结果有着提升效果,在18 维时,PCA 的性能优于CDET 的性能,根据差值图可以发现,随着信噪比的减小,差值逐渐接近;在24 维与30 维时CDET 的性能要优于PCA的性能,此时根据差值图可以发现,随着信噪比的减小,差值逐渐增大,这表明CDET 在低信噪比时有更优性能。补偿距离估计技术是根据特征向量的类间距离与类内距离的比值进行评估,虽然叠加噪声会对信号产生影响,但是通过删减冗余向量而降低叠加噪声产生的影响,基于CDET 的特征提取方法会对特征辨识度高的特征向量进行提取,因此基于CDET 的特征提取方法具备一定的抗噪性能。
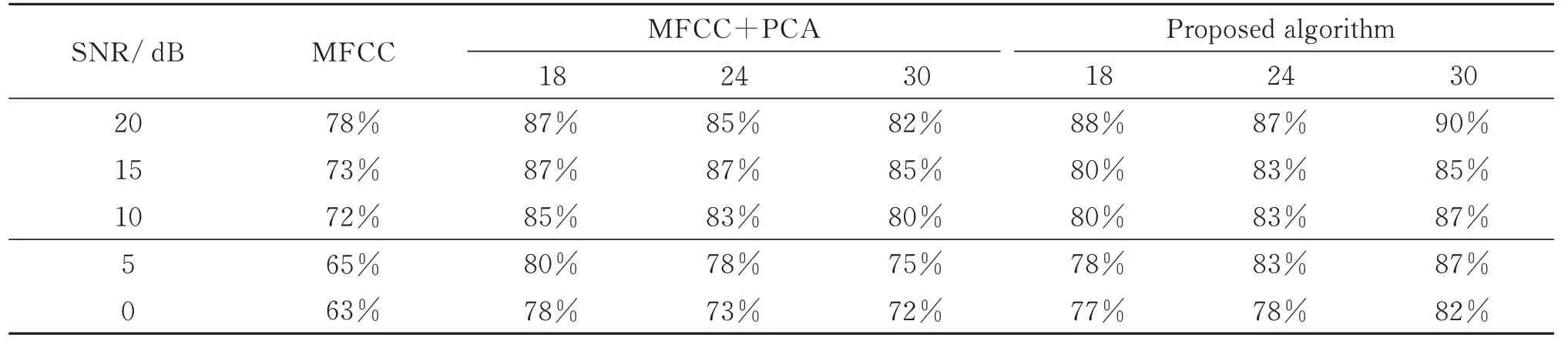
表3 不同信噪比下的分类精度Table 3 Classification accuracy under different signal-to-noise ratio


图7 不同信噪比下的准确率与差值图Fig.7 Accuracy and accuracy difference under different signal-to-noise ratio
3 结论
本文针对光纤传感振动信号易被噪声淹没,特征弱且难以表征等问题进行研究,提出了一种基于补偿距离估计技术的特征提取方法,以实现对光纤传感振动信号的有效识别。该方法在从光纤振动信号中借鉴人类听觉认知机理,提取MFCC 特征向量的基础上,并利用CDET 对特征进行评估和优化。在光纤传感振动信号识别中,该算法较传统MFCC 特征提取方法而言,通过删减冗余信息,突出有效性强、贡献率大的特征向量,解决维数过多导致的复杂运算问题并提高分类准确性。实验结果表明,该方法提高了光纤传感振动信号模式识别的有效性和实时性,对比PCA 降维处理方法而言,低维度时性能相同,随着维数的增多,CDET 的性能更加稳定。通过本文所提方法能够有效提高光纤振动信号的MFCC 特征向量在SVM 分类器中的识别正确率,提升分类系统性能,且算法具备一定的抗噪性能。

