基于多区间参数修正的角速率姿态算法

梁 哲, 周召发,*, 徐志浩, 吕文亭, 段 辉

(1. 火箭军工程大学导弹工程学院, 陕西 西安 710025; 2. 火箭军工程大学兵器发射理论和技术国家重点学科实验室, 陕西 西安 710025; 3. 中国人民解放军92281部队, 山东 青岛 266000)

0 引 言

惯性导航与卫星导航的方式相比,具有高自主性,高可靠性,高隐蔽性,长时间导航等优点,姿态解算则是惯性导航过程中的核心环节,传统的捷联惯导姿态算法主要包括欧拉角法、方向余弦法、四元数法和等效旋转矢量法,鉴于上述各个方法的优缺点,目前主流的算法为后两者。并且,利用方向余弦法和四元数法实现高精度计算结果的条件较为苛刻,而等效旋转矢量法相较于四元数法有着计算量小,容易得到理想计算精度的特点,成为目前最常用的姿态算法。

基于Bortz方程,学者们对旋转矢量算法已经进行了大量研究,提出多种优化和改进算法,但这些算法大多都是在惯组输出是角增量的条件下提出的。随着光纤技术的发展,成本相对更低的中、高精度光纤捷联惯导系统被越来越广泛地应用于军事和民用领域,对于某些低成本的干涉式光纤捷联惯导,其陀螺的输出量可视为角速率信息,导致传统的角增量多子样旋转矢量算法不能直接对其应用。若简单地对角速率进行多项式拟合-积分得到角增量信息,再代入传统算法进行姿态更新,则会使传统算法的性能大大降低。

针对上述问题,国内外多名学者先后提出了角速率表示的角速度多项式拟合方法和基于角速率的圆锥误差补偿结构,并在圆锥运动环境下优化出了补偿系数;这类算法在原理上大致相同,都是将角速率子样直接与角增量(通过对角速率拟合-积分提取)或者不同时刻的角速率进行不同形式的叉乘运算来构造补偿结构,然后在锥运动环境下进行优化得到补偿系数。与传统的角增量多子样算法相比,改进后的算法精度得到明显提高,并且能够满足实际工程应用。但部分算法提取角增量时需要大量的角速率信息,致使算法的姿态更新频率降低。

本文将在惯组输出为角速率的情况下,参考单子样姿态算法的思路,在角速度多项式拟合过程中利用前周期的部分角速率子样信息,通过对多个不同拟合区间的角速度多项式积分来提取对应采样周期的角增量信息,进而利用角速率信息和多次修正后的角增量信息构造圆锥误差补偿结构,以提高传统角速率姿态算法的解算速度和姿态解算精度。文章最后在圆锥运动环境下对新方法与传统角速率姿态算法的解算精度进行比较。

1 圆锥运动及误差描述

圆锥运动被认为是最为苛刻的导航环境,在锥运动下优化得到的不可交换误差补偿系数可用于一般角运动情况。圆锥运动角速度可描述为

(1)

式中:半锥角和圆锥运动频率均为常数,表明载体在轴上和轴上做同频但相位差90°的正弦角运动,导致在轴上输出常值角运动。其对应的姿态四元数为

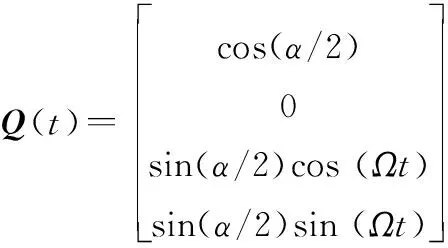
(2)

由于不能直接得到单位姿态更新时间段[-1,]内的等效旋转矢量()(其中,=--1为姿态更新周期),通过比较对应时间段内的变换四元数(),可求得()的近似值(一般看作理想旋转矢量):

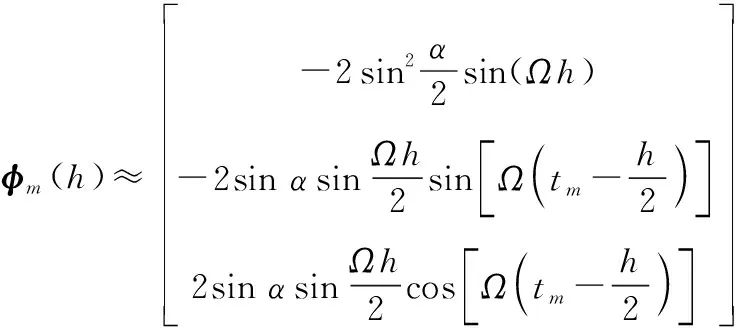
(3)

根据式(1)积分可得单位姿态更新时间段[-1,]内的角增量为

(4)

根据式(3)和式(4),学者基于角增量输入情况提出的圆锥优化方法通式为

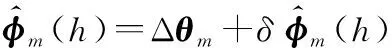
(5)

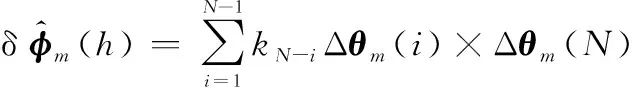
(6)

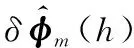
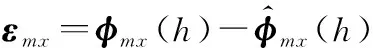
(7)

将进行泰勒级数展开,令低阶项的系数为零,即可求出圆锥优化补偿系数矩阵,有

=[,,,…,-1]

(8)

综上所述,圆锥优化补偿算法目的是在理想环境下,利用各姿态参数的理论值优化出最优补偿系数,再将所求系数应用于一般角运动情况,从而提高传统等效旋转矢量算法的精度。

但针对角速率输入的情况,若简单地对角速率进行多项式拟合-积分得到角增量信息,再代入上述算法进行姿态更新,则会使算法的性能大大降低。接下来将会对某一含有角速率信息的圆锥误差补偿结构进行具体描述,并分析其目前所存在的不足。

2 角速率输入圆锥补偿算法

针对上述问题,有学者提出一种基于角速率输入的圆锥补偿算法,算法通式参考式(5),其中,

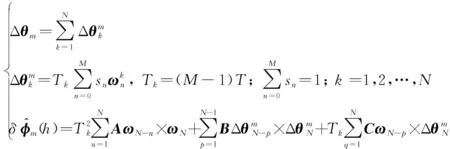
(9)

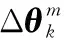
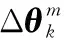
虽然该算法相较于传统的角速率圆锥补偿算法有着明显的精度优势,但因其在子样计算条件下所需的角速率子样数是传统算法的倍,导致姿态更新周期至少延长-1倍,失去了传统算法的高实时性优势。

3 多区间角增量修正姿态算法

根据第2节中所提补偿算法推导过程的分析结论和其存在的不足,本节探讨一种角速率输入条件下基于多区间角增量滞后修正的姿态解算方法。

3.1 类单子样拟合方法原理

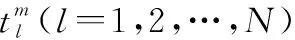
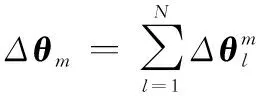
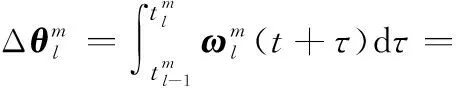
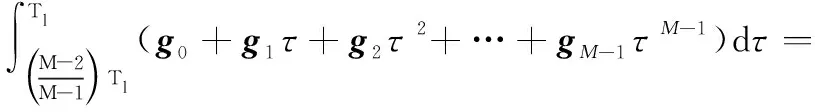
T=()=()=

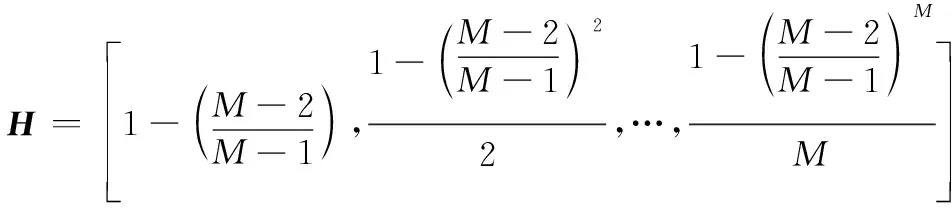
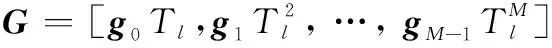
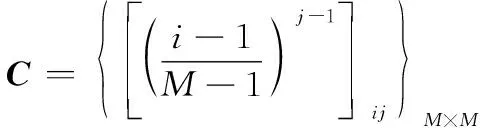
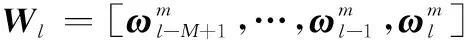
=(-1),=1,2,…,

构造圆锥补偿项:

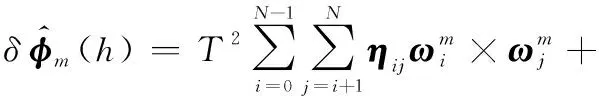
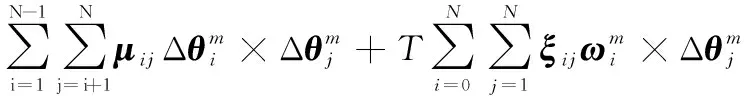
(10)

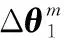
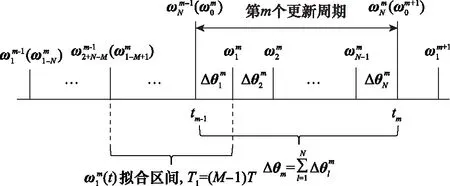
图1 类单子样算法时间关系示意图Fig.1 Schematic diagram of the time relationship of a class of monadic algorithms

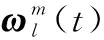
(11)

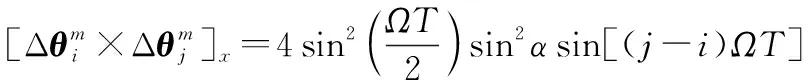
(12)

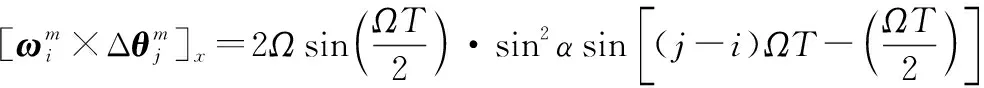
(13)

经过简单的推导,式(10)可化简为

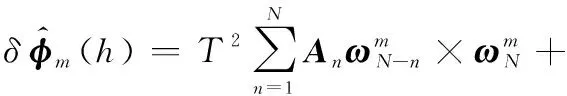
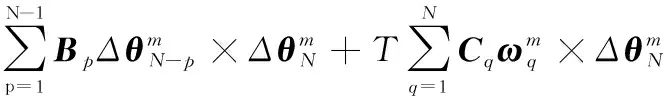
(14)

式中:、和为最终所求各化简叉乘项的圆锥误差补偿系数。其可进一步表示为

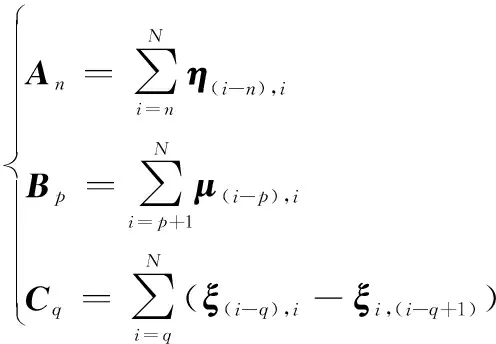
(15)

最优补偿系数的求解过程为

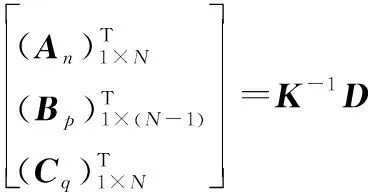
(16)

其中,

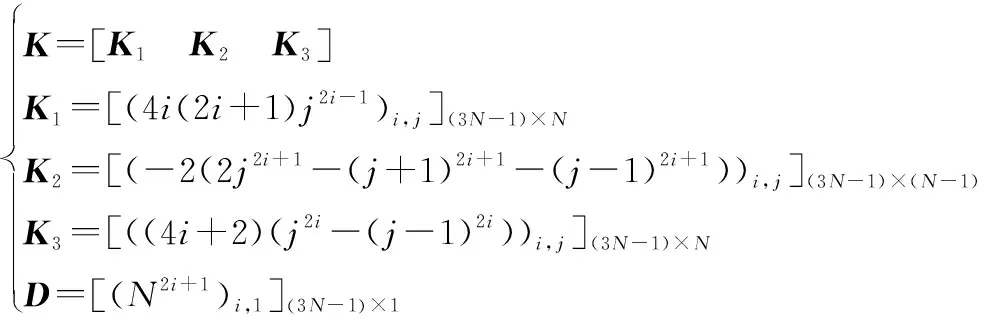
(17)

值得指出的是,式(10)在理论值环境下化简到式(14)的过程也与第1节中所提圆锥优化补偿算法的基本思想相一致。

根据上述推导分析,现给出1～3子样算法的补偿系数如表1所示。

表1 1～3子样算法的补偿系数

3.2 角增量滞后修正方法

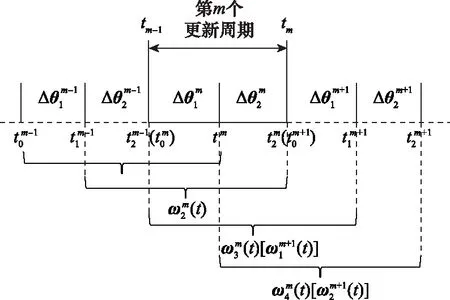
图2 角增量滞后修正示意图Fig.2 Schematic diagram of angular increment lag correction

分析图2可知,每个角增量Δ可由-1个角速度多项式()在对应的单位采样周期内积分求均值得到,即

(18)

(19)

相较于传统算法使用单个多项式拟合的角增量提取方法,该方法所求的角增量包含更多的角速度变化信息,因而可在一定程度上提高角增量的计算精度。

4 姿态算法计算量分析

本节将从叉乘运算次数,拟合积分运算次数和信息复用次数3个方面进行计算量分析。为方便分析,记第2节中的算法为算法1(简记为Alg1),记第3节算法为算法2(简记为Alg2)。Alg1算法中拟合角速率数量记为1,角增量数量记为1;Alg2算法中拟合角速率数量记为2,角增量数量记为2。令导航周期为,且1=2,1=2。

对于Alg1算法,从式(9)可看出,在单位更新周期1=1内,误差补偿项要进行(31-1)次叉乘运算,进行1次拟合积分运算,信息复用次数为0。则Alg1算法在导航周期内的叉乘运算次数为

=(1)·(31-1)

(20)

积分拟合运算次数为

=(1)·1

(21)

信息复用次数为0。

对于Alg2算法,从式(10)、式(18)、式(19)可看出,在单位更新周期2=2内,误差补偿项要进行(32-2)次叉乘运算,进行2·2次拟合积分运算,分析图2可知,信息复用次数为2·(2-2)。则Alg2算法在导航周期内的叉乘运算次数为

=(2)·(32-2)

(22)

积分拟合运算次数为

=(2)·2·2

(23)

信息复用次数为

=(2)·2·(2-2)

(24)

但是对于当今计算机的计算速度来说,式(20)～式(24)的计算时间远小于姿态更新周期,更新周期是影响算法实时性的主要因素。则导航周期内Alg2算法和Alg1算法的姿态更新的频率比值可示为

12=-1

(25)

5 仿真与分析

圆锥运动环境仿真的参数设置为:圆锥频率=1 Hz,圆锥半锥角的变化范围为0.01″～90°,导航时长设置为1 min,角速率采样间隔分别设置为5 ms、1 ms,利用4阶多项式对角速率进行拟合。经过仿真,导航周期内在常值轴上的最大漂移误差分别如图3、图4所示,实线为Alg1算法的常值漂移误差,虚线为Alg2算法的常值漂移误差,各图例与子样数的对应关系依次为=2～5。

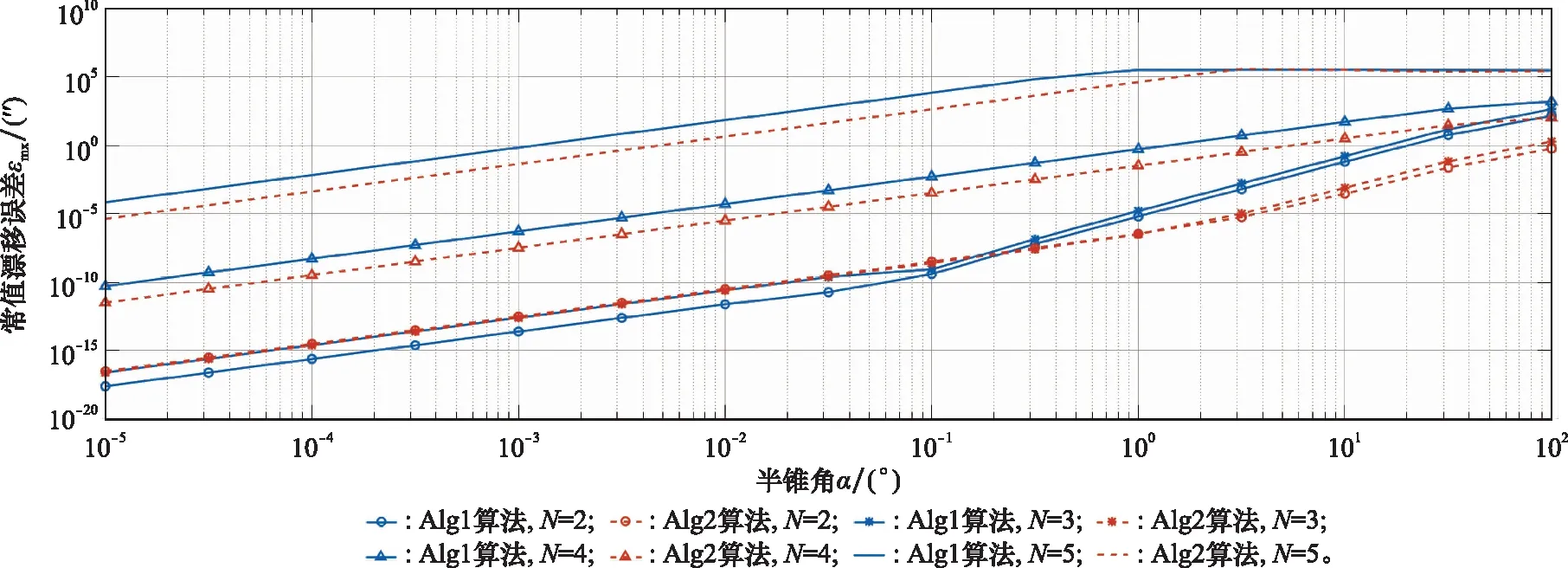
图3 T=5 ms时常值漂移误差Fig.3 Constant drift error when T=5 ms

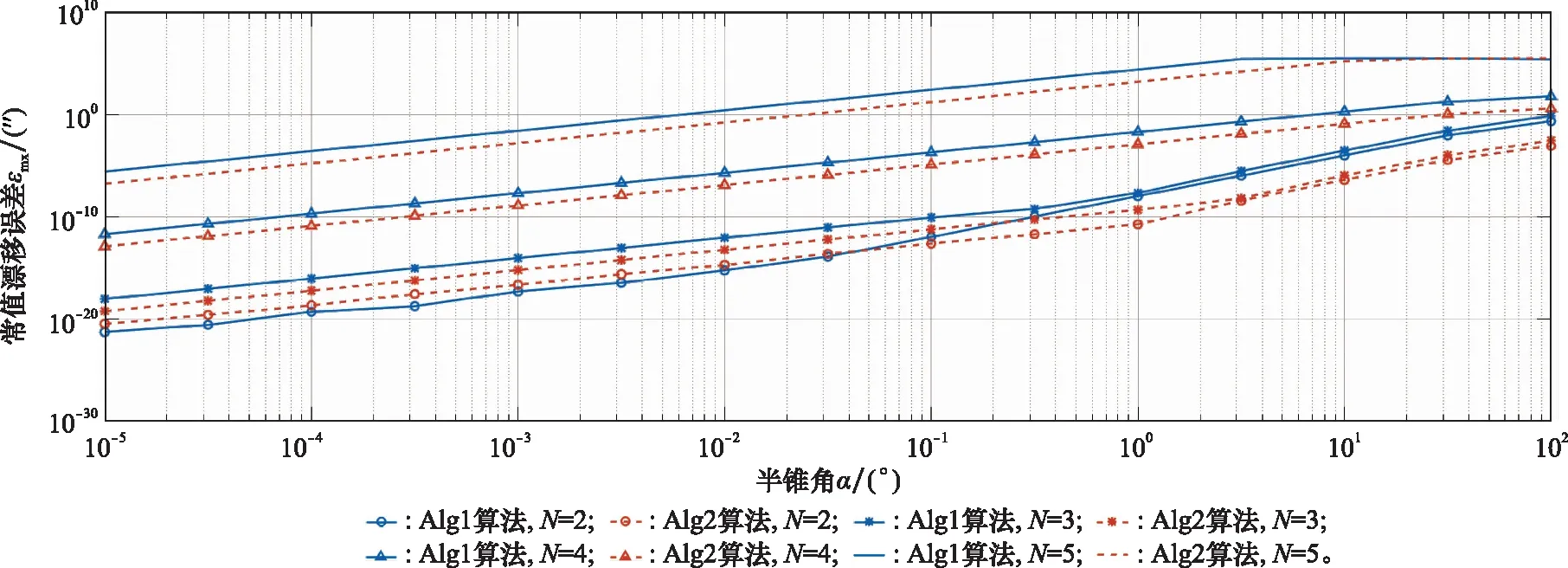
图4 T=1 ms时常值漂移误差Fig.4 Constant drift error when T=1 ms

观察分析图3、图4可以得出以下结论:

当子样数=2时,Alg2算法和Alg1算法的计算精度均最高;且随着子样数的增加,两种算法的计算精度均逐渐下降;随着采样频率从200 Hz增加至1 000 Hz,两种算法在不同子样数下的计算精度整体提高1～3个数量级。

采样频率为200 Hz的情况下,子样数=2～3时,在<0.5°的小半锥角范围内,Alg2算法的计算精度略低于Alg1算法;在=0.5°～90°的大半锥角范围内,Alg2算法最高高于Alg1算法的计算精度3个数量级;且在这两种子样数下Alg2算法的计算精度接近。子样数=4时,Alg2算法的计算精度整体高于Alg1算法1个数量级。子样数=5时,在半锥角<2°范围内,Alg2算法的计算精度整体高于Alg1算法1个数量级;在半锥角>2°范围内,Alg2算法的计算精度与Alg1算法相当。

采样频率为1 000 Hz的情况下,子样数=2时,在<0.08°的小半锥角范围内,Alg2算法的计算精度略低于Alg1算法;在=0.08°～90°的大半锥角范围内,Alg2算法最高高于Alg1算法的计算精度3个数量级。当子样数=3～4时,Alg2算法的计算精度整体高于Alg1算法1个数量级。子样数=5时,在半锥角<10°范围内,Alg2算法的计算精度整体高于Alg1算法1个数量级;在半锥角>10°范围内,Alg2算法的计算精度与Alg1算法相当。

为了进一步验证新算法的性能,在采样周期为=04 ms,子样数=2,利用4阶多项式对角速率进行拟合的条件下,将圆锥频率的范围设置为1～1 000 Hz,在常见的小半锥角=0.01°,0.1°,1°情况下分别进行仿真实验,比较两种算法的性能,对比结果如图5所示。

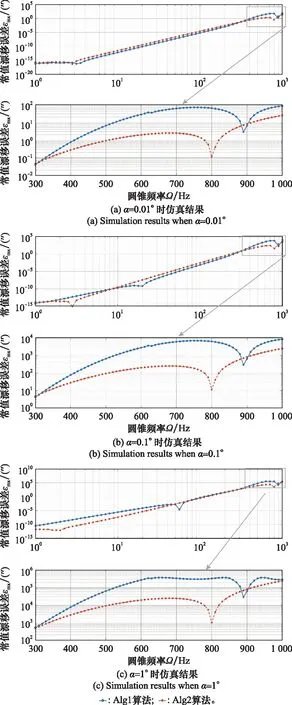
图5 T=0.4 ms时不同小半锥角条件下算法性能对比Fig.5 Algorithm performance comparison with different smallhalf-cone-angles when T=0.4 ms

除上述在小半锥角条件下的仿真分析之外,在大半锥角=10°,30°,50°,70°,90°的情况下也分别进行仿真实验,比较两种算法的性能,对比结果如表2所示。

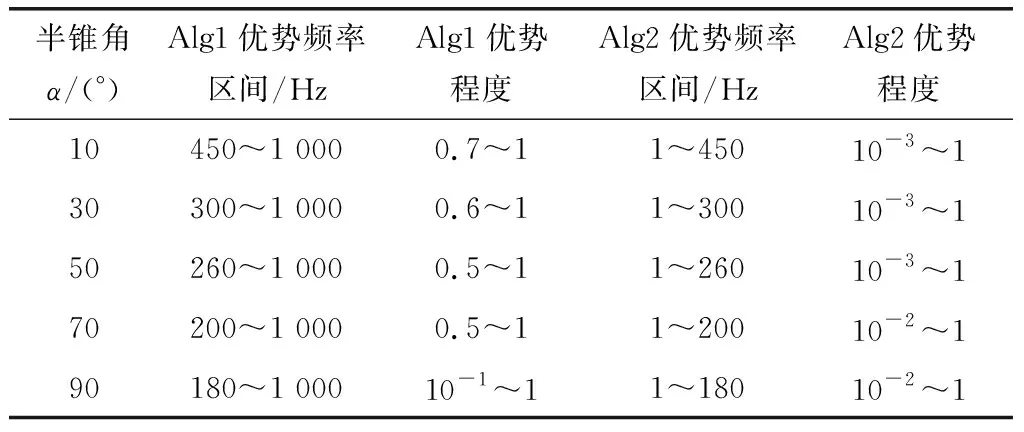
表2 T=0.4 ms时不同大半锥角条件下算法性能对比

表2中，“Alg1优势程度”=(Alg1)(Alg2),“Alg2优势程度”=(Alg2)(Alg1)。

小半锥角条件下,分析图5可以得到以下结论:

由图5(a)可观察到,在圆锥频率=1～300 Hz范围内,Alg2算法的计算精度整体略低于Alg1算法,在圆锥频率=300～1 000 Hz范围内,Alg2算法的计算精度整体高于Alg1算法0～3个数量级,特别地,在圆锥频率=885～905 Hz范围内,Alg1算法的计算精度高于Alg2算法不到0.5个数量级;由图5(b)可观察到,在圆锥频率=1～9 Hz和Ω=300～1 000 Hz的范围内,Alg2算法的计算精度整体高于Alg1算法0～3个数量级,在圆锥频率=9～300 Hz范围内,Alg2算法的计算精度整体略低于Alg1算法,特别地,在圆锥频率=885～905 Hz范围内,Alg1算法的计算精度高于Alg2算法不到0.5个数量级;观察图5(c)可知,在圆锥频率=1～50 Hz和=70～1 000 Hz的范围内,Alg2算法的计算精度整体高于Alg1算法0～3个数量级,在圆锥频率=50～70 Hz的小范围内,Alg2算法的计算精度低于Alg1算法0～3个数量级,特别地,在圆锥频率=885～905 Hz范围内,Alg1算法的计算精度高于Alg2算法不到0.5个数量级;随着半锥角的增大,在圆锥频率=1～300 Hz的范围内,Alg2算法的整体计算精度逐渐优于Alg1算法计算精度,且在=300～1 000 Hz范围内Alg2算法的计算精度优势保持不变。

大半锥角条件下,分析表1可以得到以下结论:

(1) 在Alg1算法的精度优势频率区间内,Alg2算法和Alg1算法的整体计算精度相差1个数量级以内,可认为在该区间内两种算法的性能接近。

(2) 在Alg2算法的精度优势频率区间内,除了相同精度的交点外,Alg1算法和Alg2算法的整体计算精度相差2～3个数量级,可认为该区间内Alg2算法的性能优于Alg1算法;且随着半锥角的增大,Alg2算法的精度优势频率区间逐渐缩短并向低频范围靠近。

6 结 论

本文在惯组输出为角速率的情况下提出一种基于多区间角增量滞后修正方法来提取角增量信息,进而构造圆锥误差补偿结构的旋转矢量姿态算法。在上述的各种仿真条件下,该算法可在提高姿态更新频率的同时,使得其计算精度在一定的圆锥频率范围内,比传统圆锥误差补偿算法的计算精度提高个2～3个数量级。仿真结果表明,新算法的整体性能优于传统算法。要想实现更高精度的导航,除了提高导航信息的提取精度之外,提高惯性器件的测量精度也越来越重要,现有捷联惯导的器件噪声也是限制高精度姿态算法(如基于毕卡迭代和多项式迭代的姿态算法)性能的主要因素。