面向复杂关联测控需求的冲突规避调度算法
辛立强, 张 超,*, 赵灵芝, 刘建平
(1. 西安交通大学信息与通信工程学院, 陕西 西安 710048;2. 西安卫星测控中心宇航动力学国家重点实验室, 陕西 西安 710043)
0 引 言
在空间资源开发热潮的推动下,我国在轨运行的中、低轨道卫星越来越多,而目前测控资源却是有限的,新建、维护测控资源设备所需成本巨大。因此,如何充分利用现有测控站网设备资源,提高测控站网资源使用的效率,尽可能地提高卫星用户测控需求的成功率成为国家迫切需要解决的问题。
由于在轨卫星分布于不同轨道,而测控资源位于地面固定位置,因此卫星与测控设备的可见时间不连续,所以测控任务的可行解是离散的。同时,航天器的测控需求也日趋复杂化,任务之间存在复杂的逻辑及时序关系约束。关联约束关系使得任务的解空间大小会受到相邻任务可行解的选取而发生非线性变化,这大大提高了计算复杂度,所以很难在有限的时间内快速找到全局最优解。国内外不少机构和学者采用遗传算法对测控资源调度问题进行了研究,文献[4]将卫星过境弧段按时间先后划分为两部分,运用遗传算法在对第一部分优化调度完成的基础上,将最优解和第二部分整合并进一步优化得到最优调度解。薛乃阳等人引入微元法将可见弧段进行离散化,并采用改进的遗传算法对小规模混合卫星资源调度问题进行验证,使用3个测控设备对24颗卫星的125个任务进行测控,将测控任务满足率由85.6%提高到92.8%。文献[6]将商业测控资源和国有测控资源结合起来共同为国家级测控任务和商用卫星提供测控服务,使用3个国有测控资源和3个商业测站对16颗国有卫星和8颗商用卫星进行联合测控,将测控调度收益值提升了13.12%。遗传算法虽然可以解决测控资源调度问题,但无法避免其计算复杂度高、算法运行时间长的特点,只适用于解决少量测控站、小规模卫星需求的资源调度问题。
随着测控设备数量和卫星任务数量的增多,遗传算法并不能在有限的时间内解决大规模测控资源调度问题,而启发式调度算法却可很好地应用于大规模调度问题中。Gooley综合采用混合整数规划与插入试探的启发式算法对美国卫星控制网的资源调度问题进行了详细研究。Babulescu等针对航天测控调度问题分别尝试使用了局部搜索、遗传算法和启发式调度算法对该问题进行求解,并对比分析了其调度结果。Li等采用先进先出调度算法对巨型星座测控业务进行了仿真,针对地面资源负载率、任务满意度等指标进行了量化分析。文献[13]在分析测控资源调度问题复杂性的基础上提出了元启发式的解决方案。文献[14]引入了可视窗口拥挤度、匹配度和卫星偏好偏差3个启发式因子,建立了基于特征信息的测控资源调度算法。文献[15]按照任务需求时间由短到长的启发式顺序安排任务能够获得较高的任务成功率。凌晓东等设计了基于任务优先级的面向需求的测控资源调度算法。然而使用优先级来确定任务的初始调度顺序无法客观反映测控资源的稀缺性,不能从全局角度考虑资源竞争所产生的冲突。
现有启发式调度算法还很少考虑到任务间复杂的关联性。本文特别针对相互关联的测控任务的资源调度问题进行了研究。在对航天测控资源调度过程中所涉及的测控设备、卫星测控任务、可见弧段信息进行描述的基础上,采用约束满足问题模型对卫星测控资源调度问题进行了数学化建模,创新性地设计了一种基于任务冲突规避的启发式调度算法。
1 卫星测控资源调度问题
我国现有测控资源调度实战系统统一调度所有地面站网测控设备以满足在轨卫星的测控请求。目前一般采用测控资源预分配+动态应急响应的方式,资源站网管理中心根据卫星发出的测运控需求申请生成测控计划。在预分配过程中,需要从全局最优角度考虑,尽可能提高任务调度成功率。资源预分配算法性能高低直接决定测控网的运行效益和卫星测控任务的满足率。因此需要对预分配测控资源调度算法的效率和成功率进行提高。
图1给出了测控资源调度的系统框图。
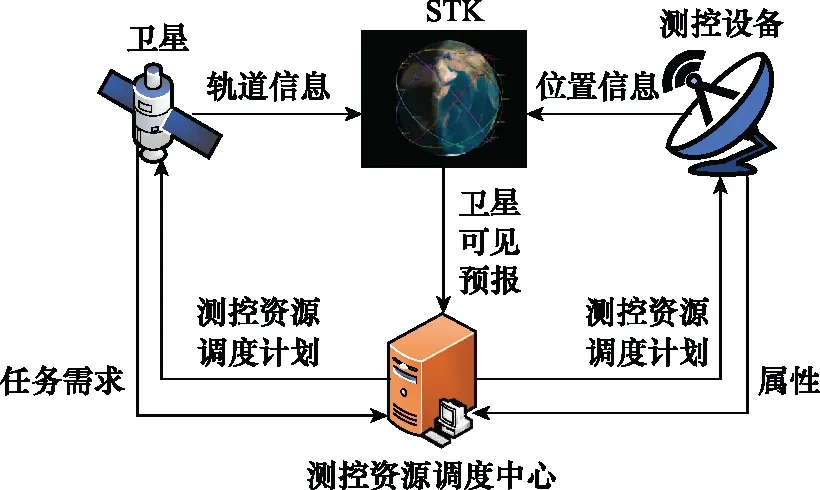
图1 测控资源调度系统框图Fig.1 Block diagram of TT & C resource scheduling system
测控资源调度问题是一种必须同时满足卫星处于测控设备可见弧段、任务需求约束的规划问题。卫星的可见弧段由其运行轨道和地面站所处位置决定。使用STK仿真软件根据卫星轨道信息和测控设备的地理位置生成卫星与测控设备的可见预报。测控资源调度中心根据具体任务需求、卫星可见预报、测控资源属性给出资源调度方案,将资源调度计划反馈回卫星和测控资源设备。
虽然近些年已经有相关学者针对我国航天测控网进行了一定的分析研究,但是未曾考虑到相邻子任务完成时间之间需要保持复杂的关联性。可行解选取不当容易导致选择的可行解违反任务间复杂的关联性约束,导致需要推倒重新选择,影响调度算法运行效率。本文根据卫星测控需求,加入了测控子任务间的关联约束,建立了目标约束满足模型。
1.1 卫星测控任务模型
现有测控资源调度系统采取预分配的调度策略,资源调度系统同时对卫星一周内的所有任务进行调度。假设一共有个卫星测控任务需求,表示所有卫星用户的测控任务集合,表达式为
={,,…,,…,}
(1)
式中:=[,,type,pri]为某一卫星的测控任务需求,为提出测控申请的卫星,为测控事件,type为星座类型,pri为该任务的优先级。={cd,1,cd,2,cd,3,cd,4,cd,5,cd,6,cd,7},中包括了一周7天的测控任务需求。假设第个任务的第天一共有(,)个子测控任务需求,那么cd, ={cd,,1,cd,,2,…,cd,,,…,cd,,(,)}。cd,,是不可分割的最小子任务需求。每个子测控任务需求cd,,有表1中的11个属性。
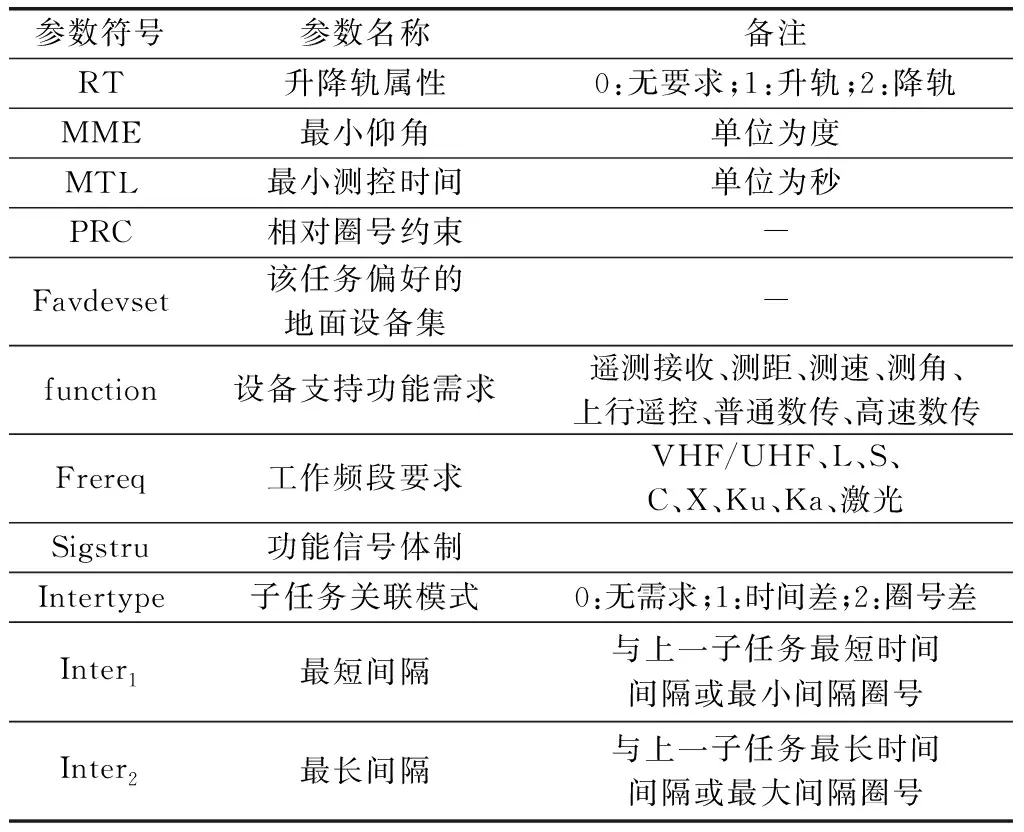
表1 任务需求属性表
cd,,可表示为
cd,,={RT,MME,MTL,RPC,Favdecset,function, Frereq,Sigstru,Intertype,Inter,Inter}
(2)
表1给出了卫星测控任务需求的基本属性。RT表示升降轨要求,指定完成该测控子任务需要卫星处在升轨弧段或降轨弧段;MME表示测控弧段所需的最小仰角;MTL表示完成该测控子任务所需的最短测控时间;RPC表示测控所属相对圈号约束,PRC⊆{1,2,…,},为卫星过境连续可见圈数,完成该测控子任务的相对圈号仅能是PRC集合中的一个;Favdevset表示该任务偏好的地面设备集;function表示该子任务需要实现的功能;Frereq表示该任务所需的频段,常用的频段有VHF/UHF、L、S、C、X、Ku、Ka、激光,只有测控设备具备该频段的通信条件时,才可完成该任务的测控;Sigstru表示该任务所需的功能信号体制;Intertype表示相邻子任务的关联模式,Intertype=0表示相邻两子任务完成圈号需满足最大最小约束,Intertype=1表示相邻两子任务的测控时间间隔需满足最大最小约束;Inter表示该子任务测控的开始时刻与上一子任务测控结束时刻的最短时间间隔或最小间隔圈号;Inter表示完成该子任务测控需求的开始时刻与完成上一子任务测控结束时刻的最长时间间隔或最大间隔圈号。
1.2 地面测控设备模型
我国卫星测控站主要分布于国土境内,各个地面站的设备属性均不相同,为规范化统一描述其属性,我们给出了卫星测控设备的基本属性,如表2所示。

表2 卫星测控站设备属性
假设有个测控设备,用集合{,,…,}表示。每个测控设备的属性可以表示为
={buildtime,diamatletime,function, Fresus,Sigsus,〈forbiddentime〉}
(3)
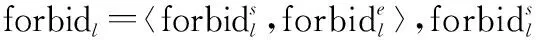
1.3 可见弧段模型
由于只有当卫星与地面测控站可见时才可进行测控任务。因此,通过仿真软件,结合卫星的轨道信息和测控资源的位置信息生成卫星的可见弧段预报。表3给出了卫星可见弧段的基本属性。

表3 卫星可见弧段预报属性
对地面测控设备和卫星相对应的可见弧段特征可描述为
={,,RF,rev,Idrev,conrev,tr,tr,Ang}
(4)
式中:表示某卫星相对于一个地面设备的一个可见弧段;表示地面设备编号;表示卫星编号;RF表示该弧段的升降轨属性;rev表示该卫星的总圈号;Idrev表示此弧段为该卫星此次过境的相对圈数;conrev表示该卫星此次过境的连续可见圈数;tr表示该弧段开始时间;tr表示该弧段结束时间;Ang表示该可见弧段中点的俯仰角。
1.4 测控资源调度目标约束模型
为建立目标约束模型,引入决策变量,,。当,,=1时,表示任务的第天的第个子任务调度成功;当,,=0时,表示任务的第天的第个子任务调度失败。完成一个测控子任务的资源利用情况可以表示为,,={cd,,,,rev,,},任务cd,,在卫星的第rev圈完成,和分别表示cd,,使用设备测控的开始时间和结束时间。当子任务未被完成时,,,=∅。我们将目标函数设计为卫星测控子任务的加权完成率最大,如下所示:
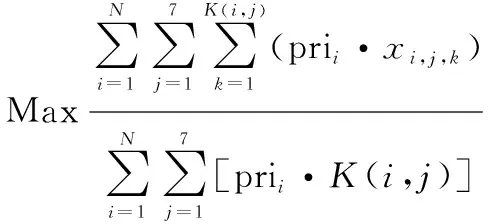
(5)
测控资源调度问题的约束条件可以分为3大类:第一类是基于测控子任务的需求约束;第二类是子任务间的关联约束;第三类是根据设备可用时间、卫星可见弧段所确定的设备物理约束。表4详细列举了各项约束。
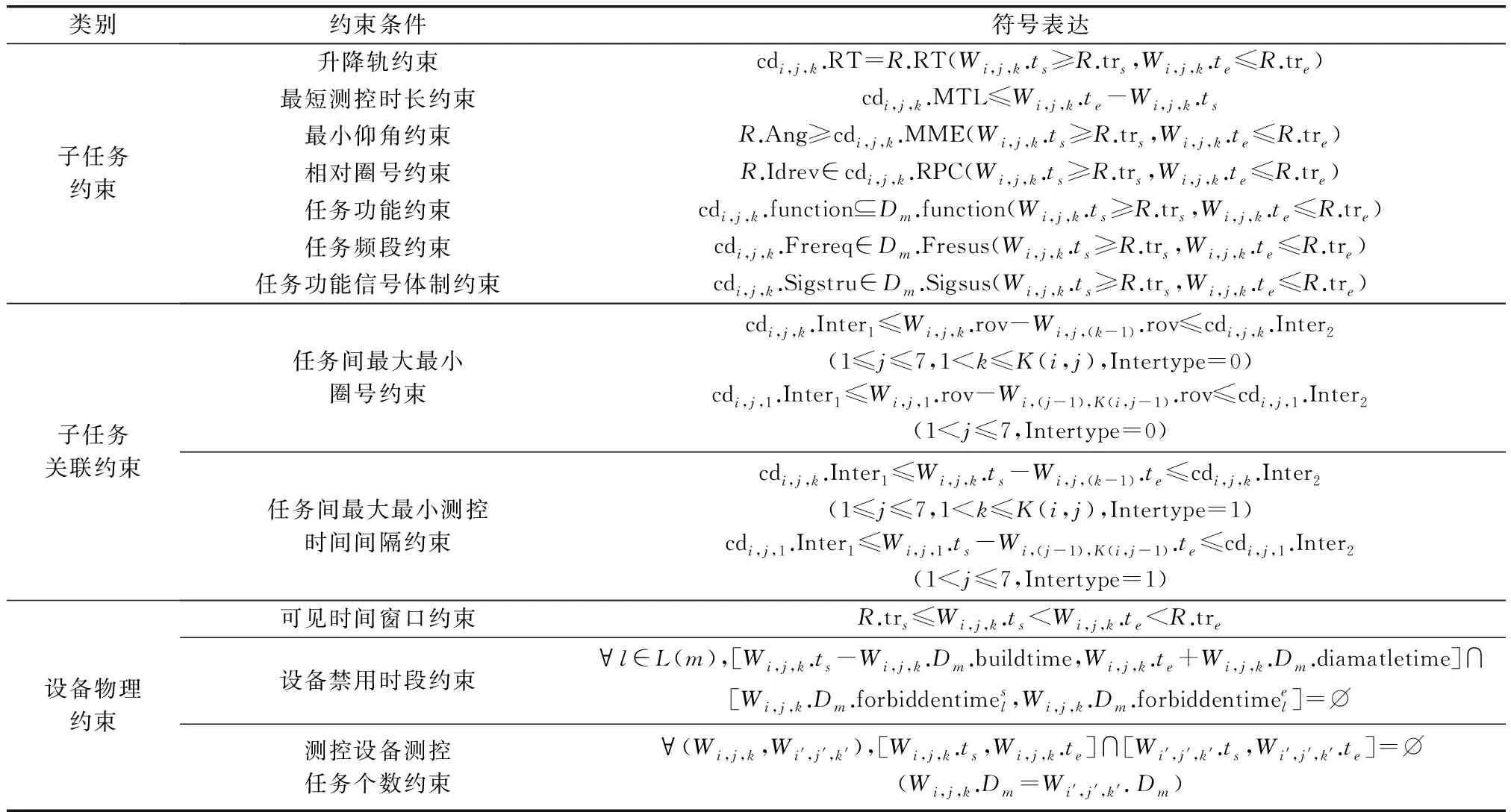
表4 测控任务约束条件表
2 测控资源调度算法
2.1 任务占用资源的概率分布
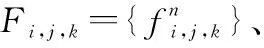

(6)
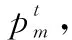
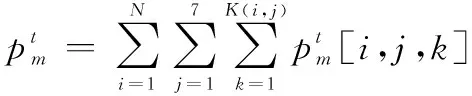
(7)
2.2 基于任务需求度的关键任务选取策略
基于启发式的航天测控网调度问题初始解生成一般包括两个步骤,即确定任务处理的顺序和任务可行解的选取策略。获得一个好的任务处理顺序是建立一个接近最优的单轮序贯调度算法的关键。
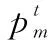
图2给出了4个设备不同时刻被任务占用概率累积和的示意图,从图中可以看出,设备3的圆圈处取值最大,即设备被任务占用概率累积和最大,说明此时该设备最可能产生任务冲突,因此为关键资源位置。
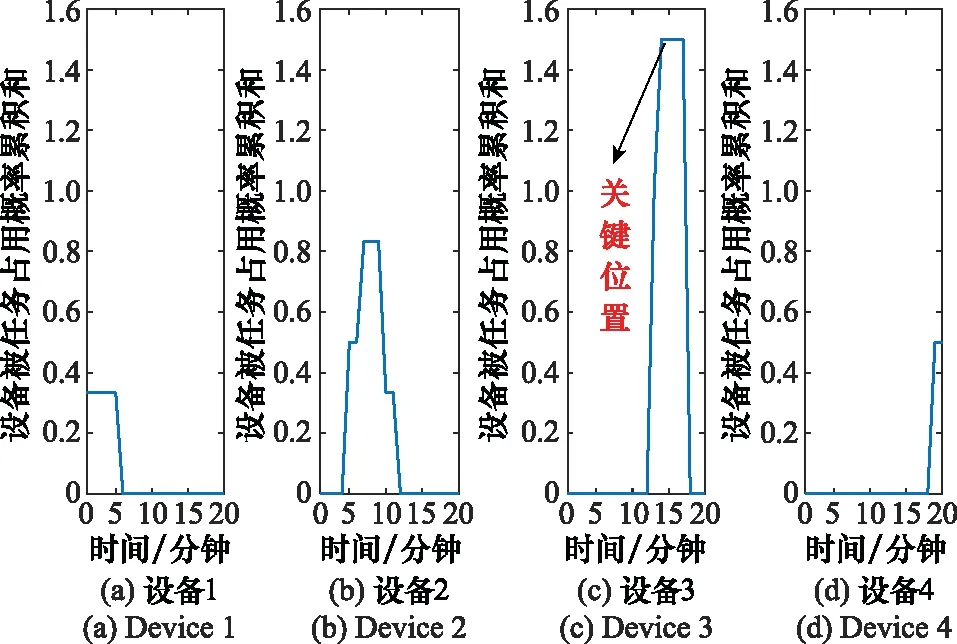
图2 关键位置示意图Fig.2 Schematic diagram of bottleneck location
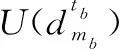
2.3 基于冲突代价最小的可行解选取策略
启发式调度算法第二步是根据可行解选取策略确定关键任务的调度解。需要综合考虑成功调度收益和导致其他任务调度失败代价,为关键任务选定最佳可行解。为方便表述,将子任务cd,,记为连续数字编号。假设通过第22节方法找到该时刻关键任务为,那么关键任务的可行解空间为。由于选择同一子任务可行解空间内的任何一个解都能够完成测控任务需求,所以该任务成功调度的收益相同。但当选择某一可行解时将导致其他待调度任务可行解空间减小情况不同,因此根据该可行解对其他待调度任务可行解空间的影响情况构造出该可行解的接受度函数()。依次遍历关键任务的所有可行解,找出其中接受度最高的解作为调度解。接受度函数()的表达式为
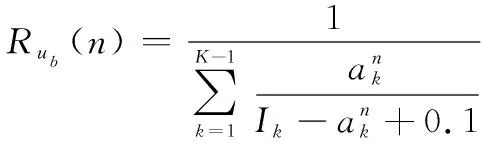
(8)
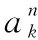
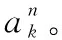
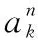
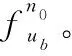
2.4 算法流程图
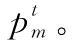
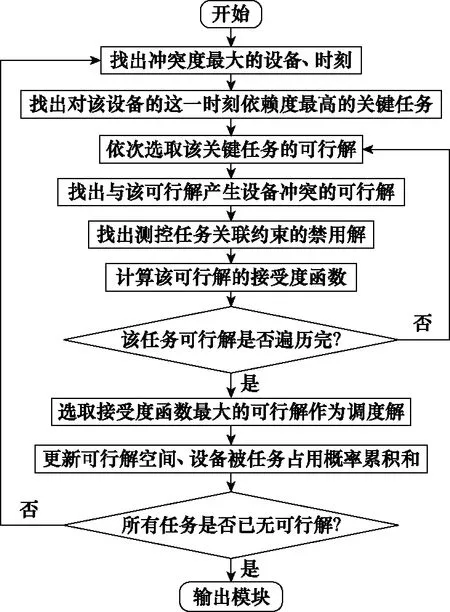
图3 算法流程图Fig.3 Algorithm flow chart
3 实验验证
为了验证本文提出的基于冲突的站网资源调度启发式算法的性能,本文给出位于9个地面站的16台测控设备对50颗、100颗、150颗低轨卫星两周14天测控任务需求进行测控的实例,分别代表小规模、中规模、大规模情况下的卫星测控任务需求。测控设备和任务需求的基本情况参见表5。
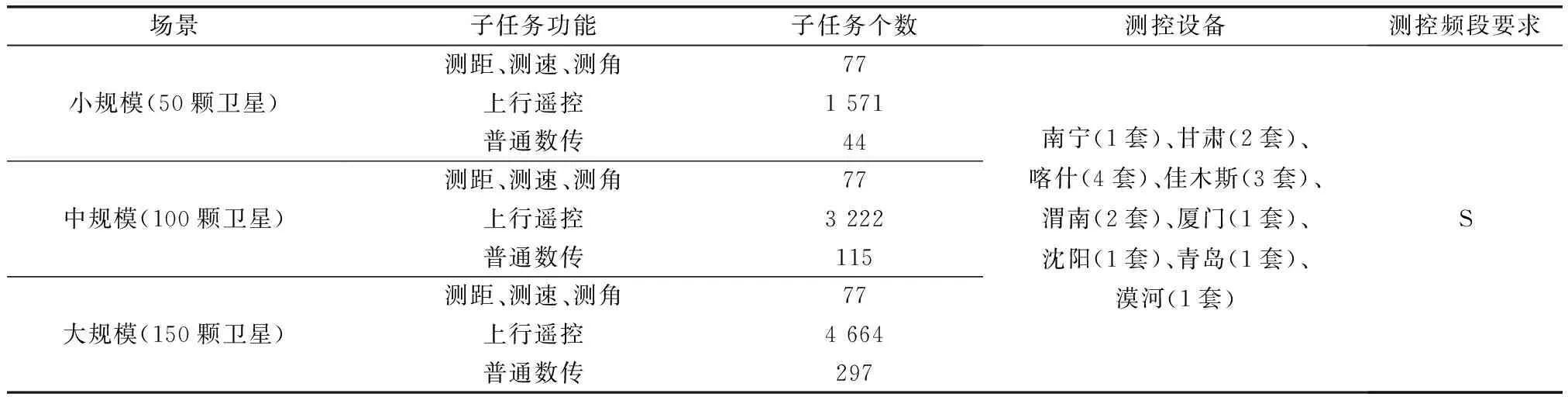
表5 测控场景的基本情况
实验验证环境为Win10 64位系统,CPU为Core i7-8700,3.20 GHz六核,16GBRAM,实验工具为Eclipse。
实验分析任务调度成功率。本文选取7组对照算法进行实验。单层调度算法采取随机选取任务的可行解进行调度和测控任务的可行解先到先服务(first in first out, FIFO)的策略。双层调度算法将对选取调度任务和可行解这两个步骤分步进行,设置基于任务优先级的FIFO算法、基于任务优先级的可行解接受度最大的调度算法、基于关键任务的FIFO算法、基于关键任务的随机可行解选取算法作为对照组。为了对比观察各个算法的性能,这里以卫星测控任务需求满足率来衡量算法的求解质量。根据上述场景实验得到不同任务规模下测控任务调度成功率如图4所示。
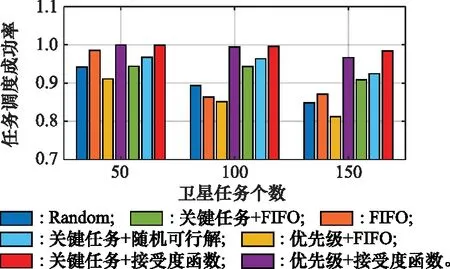
图4 不同任务规模下任务调度成功率Fig.4 Task scheduling success rate under different task sizes
从图4可以看出随机选取可行解的算法随着测控任务规模的扩大,由于其没有考虑到任务之间的冲突关系,成功率有所下降。当卫星任务个数超过100后,FIFO的调度策略成功率都低于90%,是因为其每一步选取“过分贪婪”,没有考虑到设备的稀缺性和任务可行解的灵活度,将测控任务大多安排在地方时早的设备上,使得这些设备的利用率过高,从而导致更多的任务冲突。基于任务优先级的FIFO调度算法相较于全局FIFO算法成功率有所降低,因为任务调度成功率对优先级是敏感的,而优先级的属性较为主观,也不能反映测控资源的稀缺情况。
对于采用基于关键任务的调度算法,当确定关键任务后,考虑了3种不同的可行解选取策略。FIFO的选择策略成功率最低。若随机选取关键任务的任一可行解作为调度解,任务调度的成功率随着任务规模的扩大呈下降趋势。该算法由于选择可行解时过分随机,没有考虑到子任务间有复杂的关联约束,选择不当会与未调度任务的可行解产生更多的冲突,从而降低整体任务调度的成功率。本文提出的基于接受度函数最大的测控资源调度算法由于每次选取可行解时均充分考虑到了对未调度测控任务的影响,所以该算法的调度成功率最高。随着测控任务规模的扩大,成功率依然可以保持较高水平,当有150颗卫星的测控任务需要调度时,成功率仍能达到98%以上,因此该算法是有效的。
图5给出了各测控设备的可服务时长和各算法情况下各设备提供测控服务时长总和。由于一阶FIFO算法仅从可行解的开始时间角度出发,将大量任务安排在尽量早的时间段进行测控,从而使得位于黑龙江佳木斯的6号设备的测控服务时间较长。二阶的FIFO算法中,6号设备的测控时长较长,而位于新疆喀什的15号设备的测控时长较短,未能充分利用所有的测控设备,从而降低了测控任务的调度成功率。
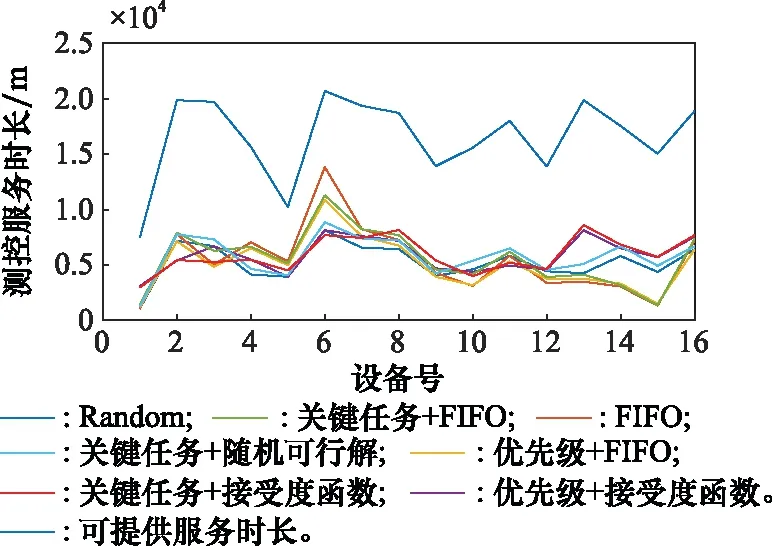
图5 设备服务时长汇总Fig.5 Summary of equipment service duration
虽然在图4中发现:基于关键任务来确定任务调度顺序并没有明显比传统的通过优先级来确定任务调度顺序的方法好。但当测控资源数量减少时,测控资源更加稀缺,便能明显体现出基于关键任务处理顺序的优势。图6展示了150颗卫星的5 038个测控任务需求在7个、10个、17个测控设备时任务调度的成功率。随着测控设备数量的减少,任务调度的成功率也随之降低。而通过基于关键任务的测控资源调度算法计算得到的任务调度成功率明显高于其他算法。
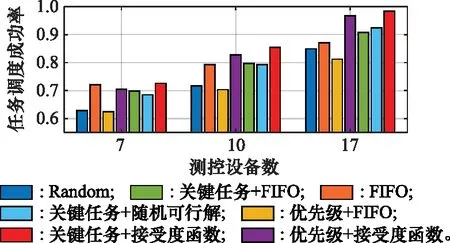
图6 150颗卫星测控任务调度成功率Fig.6 Success rate of TT & C task scheduling for 150 satellites
4 结 论
针对基于卫星需求的测控资源调度问题, 本文建立了目标约束模型,并充分考虑到测控任务需求间复杂的关联关系,设计了一种冲突规避的复杂关联测控需求调度算法。该算法采用测控资源被任务占用概率的累积和作为评判指标找到最可能产生冲突的测控设备和时刻,并选取该时刻对此测控设备需求度最大的任务作为关键任务进行调度。为避免过分贪婪,充分考虑到测控资源占用对全局任务的影响和任务间的关联关系,构造了接受度函数,选取接受度函数最大的可行解作为调度解。通过算例的对比实验分析可以看出,本算法的求解效果较好。
虽然本文提出的基于冲突规避的关键任务测控资源调度算法能够获得较为满意的调度解,但这只是一种单轮序贯的启发式调度算法。下一步将通过分析单轮序贯调度下资源分配失败任务与成功任务之间的竞争关系,设计合适的回溯搜索算法。

