基于ICPT 系统模式切换的临界负载点研究

景妍妍，王 创，蔡晓敏，韩 燕

（1.南京邮电大学通达学院电气工程学院，江苏扬州 225127；2.国网江苏扬州供电公司供电服务指挥中心，江苏 扬州 225009）

感应耦合式无线电能传输（Inductive Coupled Power Transfer，ICPT）技术利用磁场耦合原理，将电能以非导线连接的方式从供电电源侧传输到用电负载侧，是一种安全可靠、方便自动的供用电方式[1-3]，在电动汽车、便携式电子设备、机器人、无人机及特殊领域具有良好的应用前景[4-6]。

实际工作中，感应耦合式无线电能传输系统由于发射绕组和接收绕组之间存在较大气隙，造成耦合系数较低且漏感较大，系统整体的功率因数偏低[7-8]。为获得较高的传输效率和功率传输能力，通常考虑加入谐振补偿网络，使系统工作在单位功率因数。常见的补偿网络模型有SS、PS、PP 和SP 4 种简单结构[9-12]，补偿元件的引入使得系统工作在轻载时，无法实现与负载无关的输出增益，系统稳定性变差。

文中针对ICPT 系统带电阻负载在超出一定负载值后，整流电路输入侧波形畸变、断续导致系统传输效率降低的问题，提出一种将整流侧方波作为激励源，采用谐波近似法建立考虑谐波的电路模型，获得整流电路输入电压、电流的表达式，确定系统进入断续工作状态（Discontinuous Conduction Mode，DCM）的临界负载点的设计准则。

1 拓扑结构模型

典型的ICPT 系统结构如图1 所示，Uin为输入直流电压源；S1～S4为功率开关管，构成全桥逆变电路；LP、LS分别为发射绕组和接收绕组自感，M为两绕组之间互感；VD1～VD4为功率二极管，构成全桥整流电路；Cf、Lf分别为整流输出端滤波电容、电感；RL为负载电阻。其中，uAB、iIN分别为逆变电路输出电压、电流；uR、iR分别为整流电路输入电压、电流。

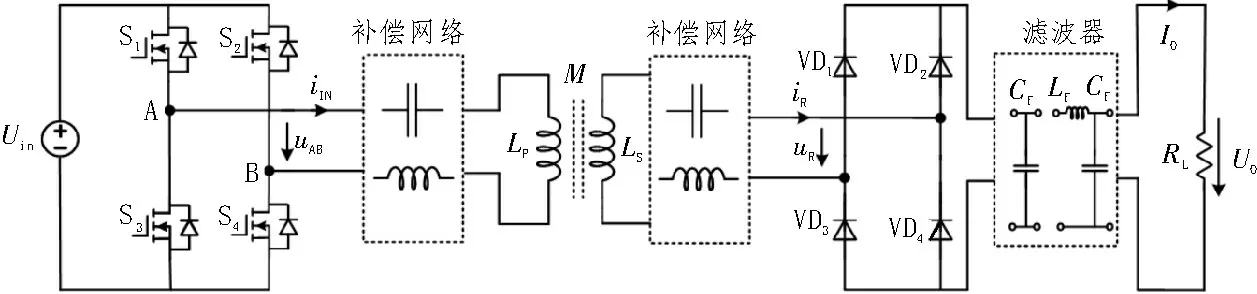
图1 典型的ICPT系统结构

基于传统基波近似法[13-14]，通常将ICPT 系统看作由逆变全桥输出方波电压uAB驱动，将电阻负载RL等效到整流电路输入侧，通过设计电路中电容和电感等元件的数值使系统工作在谐振点，以获取较好的传输效率。由于整流电路通常由非线性二极管构成，整流侧输入电压uR或电流iR的波形在超出一定负载值后，容易发生畸变，使系统进入断续工作状态。文中根据整流电路输出端采用电容滤波或感容组合滤波的方式，将ICPT 系统看作由整流电路输入方波电压源uR或方波电流源iR驱动，把逆变侧等效为纯电阻RIN，如图2 所示。根据实现与负载无关的输出恒压或恒流，可将ICPT 系统划分为4 类：1）电容滤波恒流输出；2）电容滤波恒压输出；3）感容滤波恒流输出；4）感容滤波恒压输出。这4 类电路分别对应SS、PS、PP 和SP 4 种经典补偿电路，为了简化计算，文中将以这4 种电路为例展开详细分析。

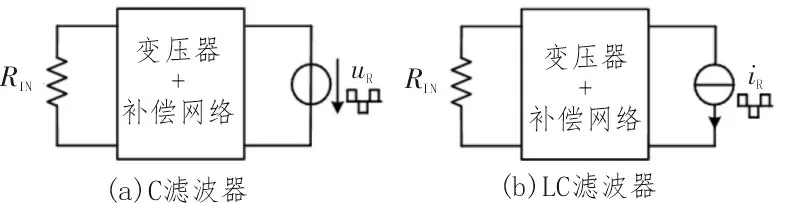
图2 ICPT系统等效结构图

1.1 电容滤波结构数学模型

SS 和PS 两种补偿网络采用电容滤波方式，此时整流电路输入电压uR为方波信号，uR的幅值取决于负载侧的输出电压Uo，相位和电流iR相同。采用互感模型的等效电路如图3 所示，为实现与负载无关的输出增益且满足输入阻抗纯阻性，发射端和接收端的补偿元件参数设计和输出特性如表1 所示[15-16]。

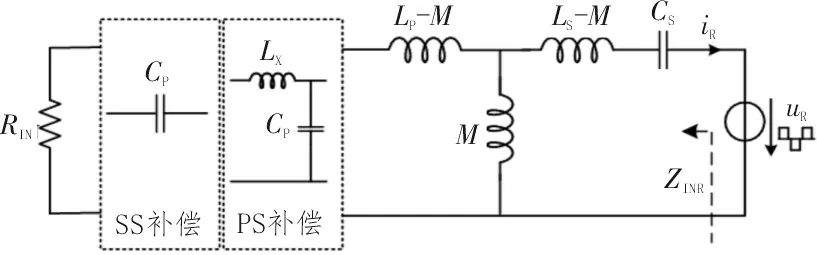
图3 电容滤波的SS、PS补偿电路

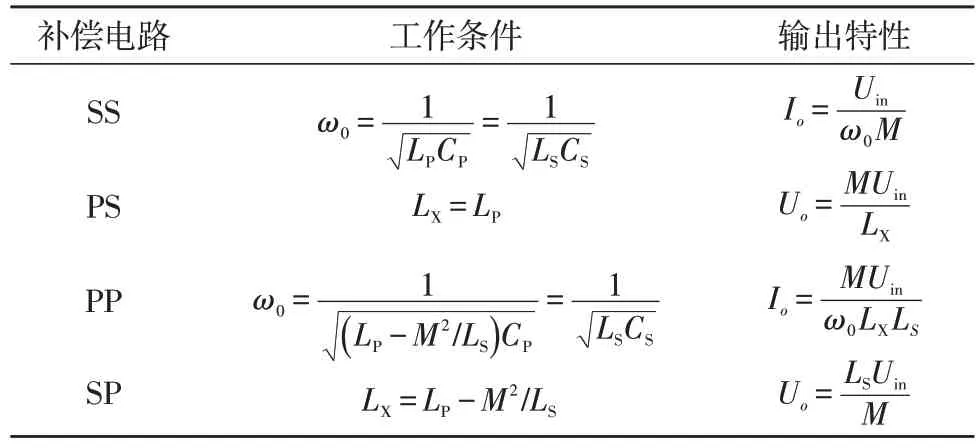
表1 4种补偿电路特性

其中，方波电压uR和电流iR含奇次谐波的傅里叶级数表达式分别为：

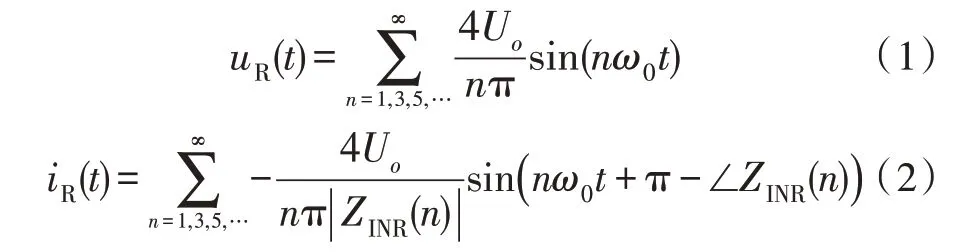
式中，ZINR为ICPT 系统在谐振频率点ω0处的反向输入阻抗，SS和PS补偿网络的n次谐波表达式为：

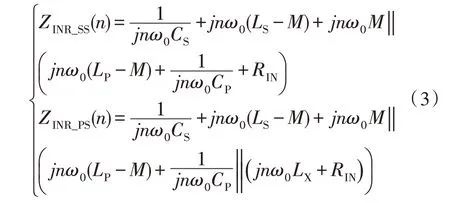
将式（3）代入式（2）中，整理得，电流iR含基波成分iR1和高次谐波成分iRH的代数和为：

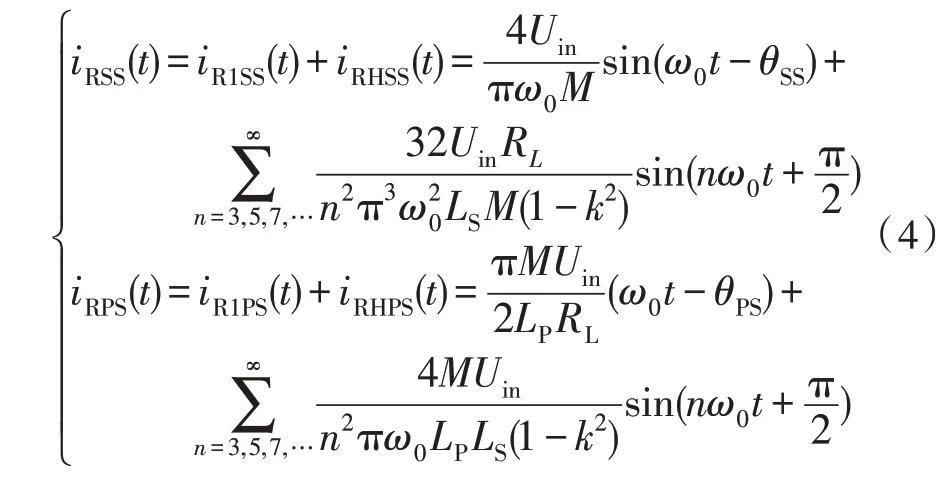
因为整流电路输入电压uR和电流iR具有相同的过零点，在t=0 时刻，存在电流iR等于0，因此基波电流滞后角θSS、θPS为：

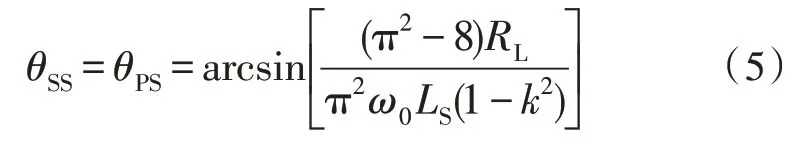
对于SS 补偿网络，随着输出负载RL增大，基波电流iR1SS幅值不受影响，基波相位滞后角θSS和高次谐波电流iRHSS幅值均增大。对于PS 补偿网络，随着输出负载RL增大，基波电流iR1PS幅值减小，相位角θPS增大，高次谐波电流iRHPS不受影响。负载为30 Ω和60 Ω时，SS 和PS 补偿网络下电流波形图如图4 所示。由图可知，当负载RL超出临界负载点RLboundary时，电流iR将出现与电压uR极性相反的情况，在不可控型器件二极管构成的无源整流电路中，该段区域将被二极管箝位至零，即iR波形出现断续，ICPT 系统进入断续工作模式。方波电压uR波形也受到谐波影响，发生畸变，导致输出增益不再满足负载无关性，输出电压Uo或电流Io的实际值与理论值的关系如表2 所示，Uref和Iref分别为ICPT 系统在连续工作模式（Continuous Conduction Mode，CCM）时输出电压和电流的理论参考值。

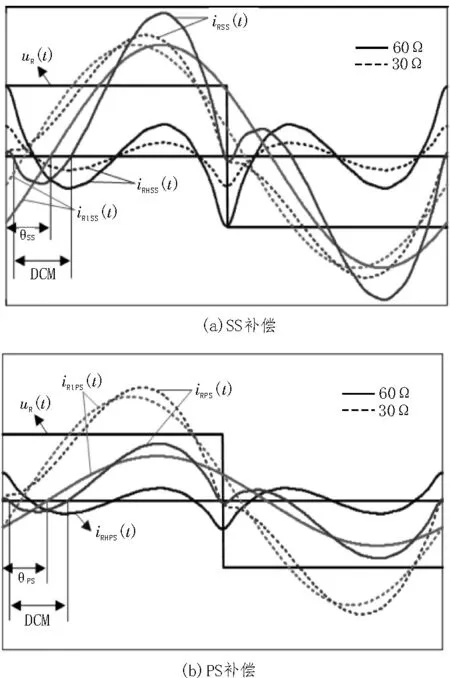
图4 电容滤波的iR、iR1和iRH计算波形图

表2 断续模式下负载侧实际输出值

1.2 感容滤波结构数学模型

相对应地，PP 和SP 两种补偿网络采用感容滤波方式，此时整流电路输入电流iR为方波信号，iR的幅值取决于负载侧输出电流Io，相位和电压uR相同。采用互感模型的等效电路，感容滤波的PP、SP 补偿电路如图5 所示，补偿元件参数设计和输出特性如表1 所示。

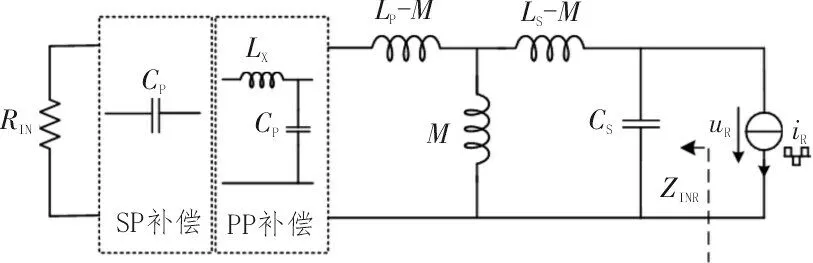
图5 感容滤波的PP、SP补偿电路

采用相同分析方法，可得PP 和SP 两种补偿网络下电压uRPP、uRSP和基波电压相位滞后角θPP、θSP表达式为：

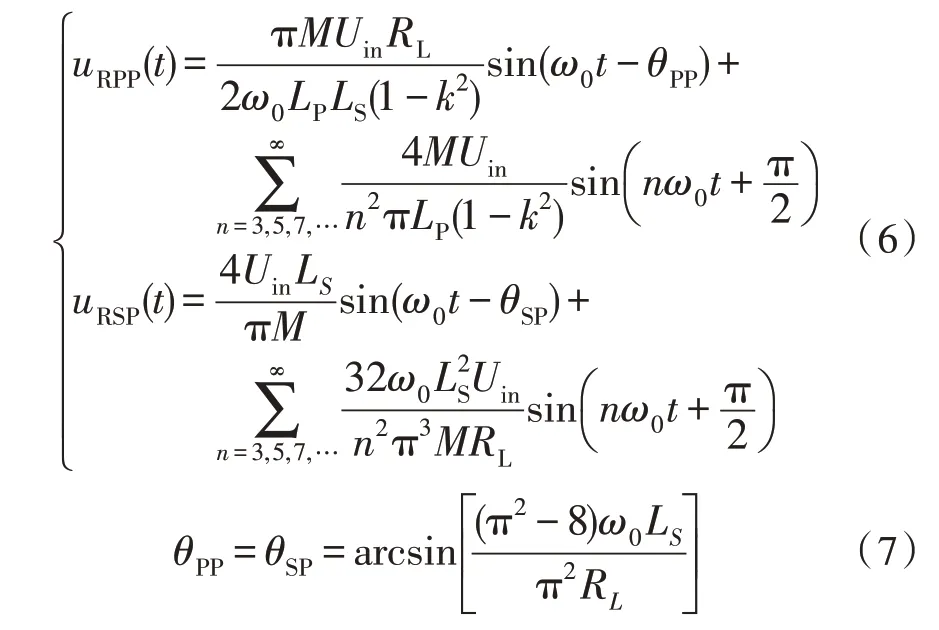
对于PP 补偿网络，电压uRPP的基波电压幅值和相位滞后角均与负载RL成正比，高次谐波电压与负载RL无关。对于SP 补偿网络，电压uRSP的基波电压幅值与负载RL无关，相位滞后角与负载RL成正比，高次谐波电压幅值与负载RL成反比。负载为10 Ω和20 Ω时，PP 和SP 补偿网络下电压波形图如图6 所示。由图可知，当负载RL超出临界负载点RLboundary时，电压uR将出现与电流iR极性相反的一段区域，电压波形在该区域断续，方波电流iR波形发生畸变，ICPT系统进入断续工作模式。负载侧输出电压Uo或电流Io的实际值与理论值的关系如表2 所示。

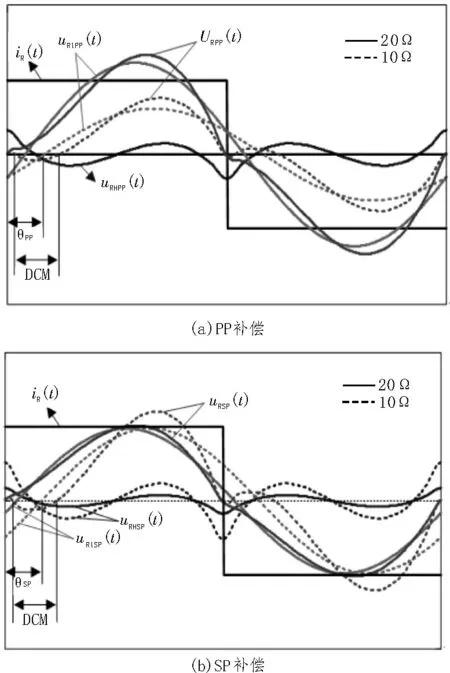
图6 感容滤波的uR、uR1和uRH计算波形图

2 临界负载点确定方法

负载RL大小直接决定ICPT 系统是否工作在连续模式，是否可满足输出增益的负载无关性。确定临界负载点RLboundary的设计流程如图7 所示。可寻找处于正半极性时，图4中电流iR和图6中电压uR波形中的最小值，若出现最小值小于零，则可判断此时负载为临界点，ICPT 系统即将进入断续工作模式。

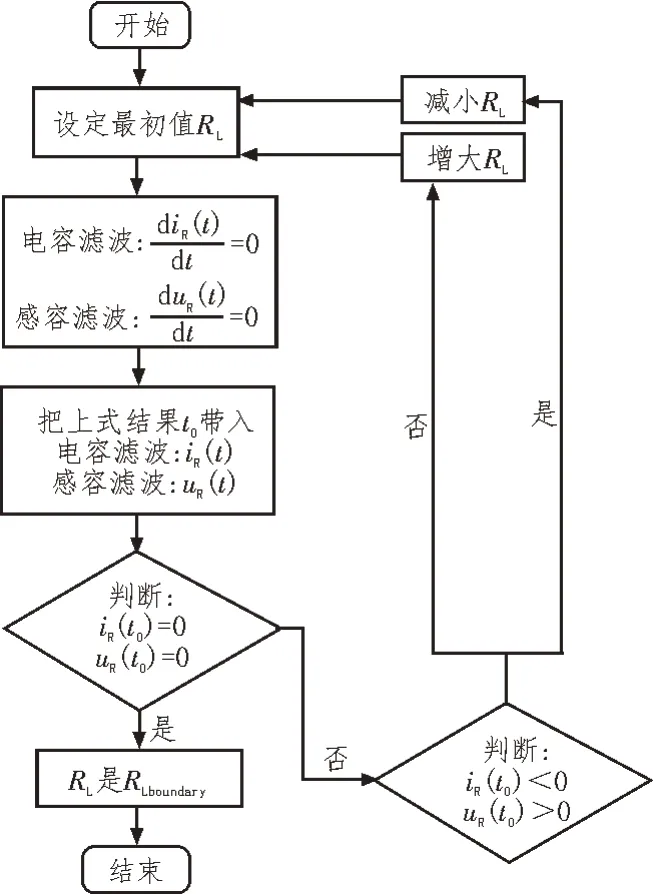
图7 临界负载点确定流程图

3 仿真分析

为了研究感应耦合式无线电能传输系统在超出负载临界点后进入断续工作状态的问题，利用Saber仿真软件观察和分析4 种补偿网络下相位滞后角和临界负载点处的电压或电流波形。设计指标为：Uin=24 V，f=200 kHz，LP=23.85 μH，LS=25.27 μH，M=16.82 μH。图8 中，负载RL的迭代步长设为1 Ω，通过计算得到SS、PS、PP 和SP 4 种补偿网络的临界负载点RLboundary分别为45 Ω、45 Ω、12 Ω和12 Ω。

由图8 可知，在连续工作模式下，对于采用电容滤波的SS 和PS 两种补偿网络，仿真结果中基波电流相位滞后角θSS和θPS亦随着负载RL的增大而增大，而对于采用感容滤波的PP 和SP 两种补偿网络，仿真结果中基波电压相位滞后角θPP和θSP亦随着负载RL的增大而减少，仿真结果均与计算结果相吻合。当超出临界负载点后，由于方波电压uR或方波电流iR发生畸变，ICPT 系统将进入断续工作模式，导致输出电压或电流增益不再满足负载无关性，仿真结果和计算结果存在较大偏差。图9 分别给出临界负载点RLboundary=45 Ω时的iRSS和iRPS、RLboundary=12 Ω时的uRPP和uRSP仿真图和计算图，用来验证上述分析的正确性。

图8 相位滞后角的仿真数据和计算数据

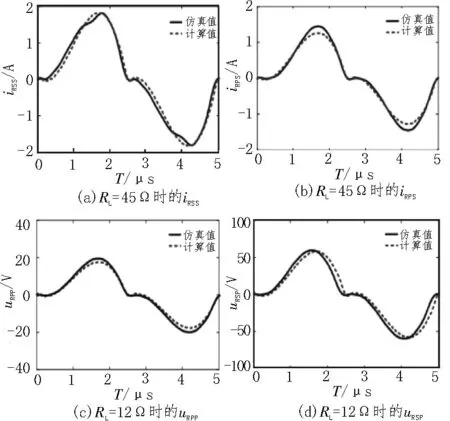
图9 临界负载点处iR、uR仿真波形和计算波形

4 结论

文中针对感应耦合式无线电能传输系统在超出临界负载点后，出现不满足输出与负载无关的恒压/恒流增益，此时系统传输效率不高的问题，从负载侧采用滤波器类型和输出增益类型分成4 类，采用谐波近似法，揭示由非线性二极管整流电路导致ICPT系统在轻载运行时易进入断续工作模式，给出临界负载点的确定准则，通过仿真验证理论分析的正确性，可为无线传输系统中其他复杂补偿网络临界负载点确定的问题，提供一定的参考作用。