燃料电池在机械应力下的工作参数分布

张恒，陈奔，隋邦傑

（武汉理工大学汽车工程学院，湖北武汉 430070）

质子交换膜燃料电池由于具有工作效率高、能量密度高和污染低等优势被视为目前最有前景的可替代清洁能源［1］.为提高燃料电池的性能，全面了解电池内部的各种传输现象是十分必要的.燃料电池包含5 个关键部件，从外到内分别为双极板（Bipolar plate，BPP）、气体扩散层（Gas diffusion layer，GDL）、微孔层（Micro-porous layer，MPL）、催化层（Catalyst layer，CL）和质子交换膜（Proton exchange mem⁃brane，PEM）［2］.由于单电池所产生的电能有限，为了满足大功率的使用要求，通常将多个单电池进行串联形成燃料电池堆，以便输出足够的功率.在燃料电池堆的装配过程中，过小的装配力会导致反应气体泄漏和产生较大的导热导电阻力［3］；过大的装配力会导致电池内部产生较高的气体传输阻力，阻碍反应气体的传输和产物水的排出，而且还会导致机械损坏［4］.在工程实际中，一般选用使GDL 产生20%形变量（载荷约为1.8 MPa）的机械力来装配燃料电池堆，此时燃料电池堆能达到最佳的工作性能［5］.Milli⁃champ 等人［3］描述了机械压缩对燃料电池中组件尺寸的影响，并总结了实现燃料电池堆最佳性能的机械压力.Chi 等人［6］用实验和理论方法研究夹紧力导致的GDL 孔隙率不均匀性对燃料电池性能的影响.Zhou 等人［7］建立了一个三维多相模型分析不均匀压缩对燃料电池内部传输参数以及对电池传输过程的影响.这些模型考虑了机械应力，但是没有考虑组件内部明显的机械形变.由于GDL 的杨氏模量较其他组件很低，所以在机械应力下，GDL 为最容易产生机械形变的组件［8］.与此同时，不同的两相流模型被建立来研究燃料电池中的液态水传输.Ince等人［9］基于XCT 实验，研究了燃料电池在不同的压力下的水传输特征，结果表明GDL 中液态水饱和度在压缩的碳纤维区域比未压缩的区域更高.Havaej 等人［10］建立了一个三维瞬态的两相流模型模拟阴极半电池的性能.Caulk 等人［11］用两相流模型研究了极限电流和液态水在GDL中的传输阻力.Vetter等人［12］用一维非等温两相流MATLAB 模型分析了从流道到催化层的液态水饱和度分布情况.但这些研究没有考虑机械应力对液态水分布的影响.

为了完善现有的两相流计算模型，本文首先求解单电池在机械应力作用下的应力分布，并将GDL内与应力形变有关的传输参数纳入新的几何模型中，得到了实际的传输性能参数［13-14］（如孔隙渗透率、电导率、热导率、接触电阻等）.然后，研究在机械应力作用下不同电流密度的液态水分布规律.此外，模型还考虑了液态水在膜中反扩散和电拖曳两种传输方式，从而能全面求解液态水在各个组件中的分布.该文的研究对燃料电池的水管理有非常重要的指导作用.在工程实践中，可以对电池内部的水分布做出精确的预测，有利于提高工程效率.

1 模型建立

本计算模型分为两部分，包括图1 所示的未受机械应力时的计算域和图2 所示的受到机械应力之后发生形变的计算域.两部分的计算域组成部件从外及内为阴阳极BPP、GDL、MPL、CL 和PEM，以及BPP 内部流道：阳极流道注入氢气，阴极流道注入空气.从图2 可以看出GDL 受到机械应力后发生了明显的形变且出现了入侵流道的现象［15-16］.

图1 受到机械应力之前质子交换膜燃料电池的几何模型示意图Fig.1 Schematic diagram of the geometric model of proton exchange membrane fuel cell without mechanical stress

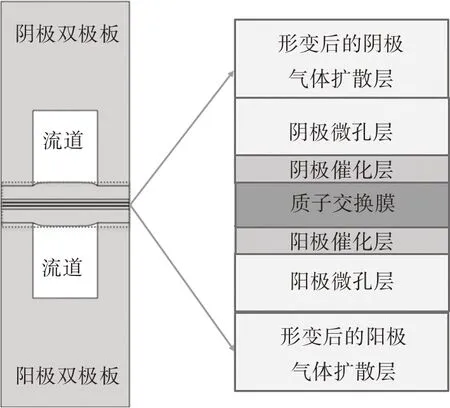
图2 受到机械应力之后质子交换膜燃料电池的几何模型示意图Fig.2 Schematic diagram of the geometric model of proton exchange membrane fuel cell under mechanical stress

1.1 模型假设

本研究中，建立了一个二维稳态的PEM 燃料电池两相流模型.为了简化计算，并保证计算的可行性，本模型基于以下假设条件［13］：

1）本模型计算是处于稳态；

2）反应气体均为理想气体；

3）MPL、CL 以及PEM 的应力形变被忽略，且传输参数均为各向同性，孔径分布均匀；

4）GDL里面的形变为弹性形变；

5）机械应力里面的湿热效应被忽略.

1.2 控制方程

GDL 在模型计算中视为可压缩的弹性材料，机械应力形变方程为胡克定律：

式中：F为压缩机械应力；E为杨氏模量；ϵ为机械应变.

电子传输方程为欧姆定律：

式中：σe为电子传导率；∅e为电子电势差；je为电子通量；i为电流密度.

质子传输方程为欧姆定律：

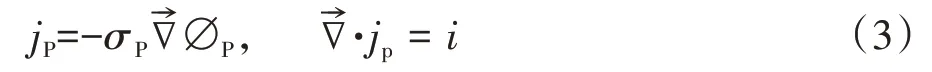
式中：σP为质子传导率；∅P为质子电势差；jp为质子通量.

热传导方程如下：

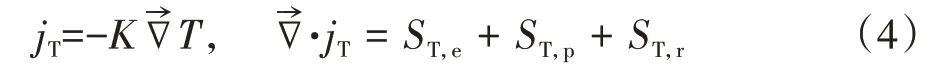
式中：K为热导率；T为温度；ST，e为电子流动产生的热源；ST，p为质子流动产生的热源；ST，r为电化学反应热源.

气体传质方程为Maxwell-Stefan方程：

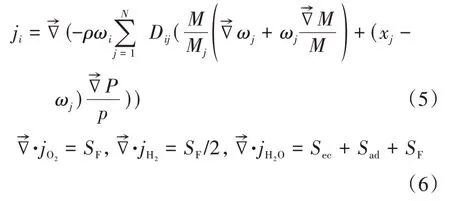
式中：ρ为密度；ωi，ωj为质量分数；Dij为二元气体的扩散系数；M为摩尔质量；xi，xj为摩尔质量分数；p为压强；SF为电化学反应源项；Sec为蒸发/冷凝源项；Sad为吸附/解析源项.

液态水的传输方程服从达西定律［17］：

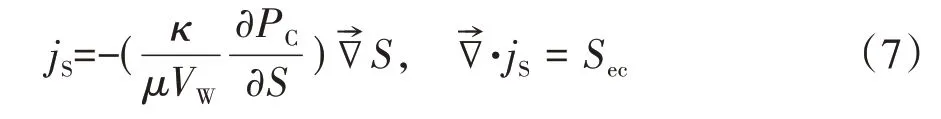
式中：κ为渗透率；μ为液体水的黏度；VW为水的摩尔体积；PC为毛细压力；S为液态水的饱和度.

气体扩散介质的毛细压力和饱和度的关系［12］：

式中：C为总间隙气体浓度；xsat为饱和摩尔分数；Psat为饱和压强.

1.3 形变修正方程

式中［6］：CR 为压缩率；Vcomp为GDL 受到机械应力压缩形变之后的体积；V为气体扩散层受到压缩之前的初始体积.

式中：εcomp为受到机械应力之后的孔隙率；ε0为初始孔隙率.

式中：Κ为热导率；Κs为固体纤维的热导率；ΚF为流体的热导率.当Κs≫ΚF时，我们可以将式（18）简化为式（19）.

式中：ϰcomp为渗透率；其中Ck为Kozeny 常数（Ck=6）；Dr为气体扩散介质中的平均孔直径（Dr=7×10-6m）.

式中［18］：r为气体扩散层与双极板之间的接触电阻率（mΩ·cm-2）；p为双极板与扩散层之间的接触压力（Pa）；A，B，C均为常数（A=3.32 mΩ·cm-2，B=1.01 MPa，C=0.534）.

1.4 液态水饱和度修正方程[14]

式中：S为液态水的饱和度；εl为考虑液态水之后的孔隙率；τl为考虑液态水饱和度之后的曲率；Κl为液态水饱和度修正之后的热导率；ϰl为液态水饱和度修正之后的渗透率.

1.5 源项

表1 为本模型计算公式的源项汇总，包含多孔介质层（GDL、MPL、CL）和PEM.

表1 计算模型的源项Tab.1 Source terms of the computational model

在电池的阳极氢气发生氧化反应产生质子和电子，此为电子和质子的源项.在电池的阴极氧气和阳极产生的电子和质子发生还原反应产生水.在本文中，假定反应产生的水均为气态水SF.

氧气的消耗为SF/2，氢气的消耗为SF.Sad为在CL里面液态水和离聚物形态的水转换的源项：

式中：κa和κd分别为吸附和解吸质量传输系数；L为催化层厚度；Vm为离聚物摩尔体积，λeq为离聚物中水的等效含量，λ为离聚物的水含量.

离聚物中水的等效含量λeq表达式为［19］：

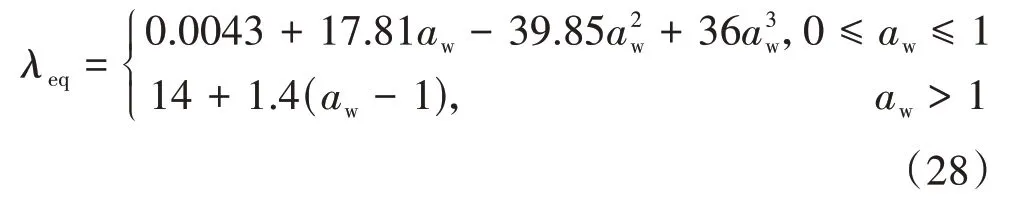
式中：aw是水蒸气活度（本质是相对湿度）且aw=是水摩尔浓度；Mn 为聚合物的等效质量；ρdry为聚合物的干态密度.

气相水和液相水的相变转化，由以下转变方程式决定［12］：

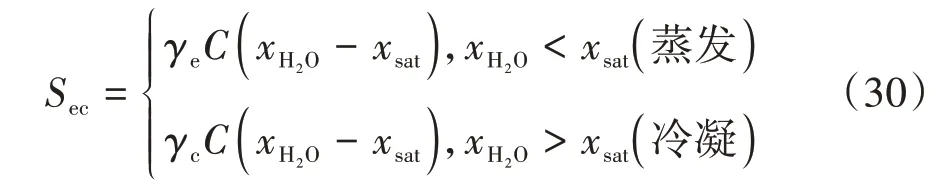
式中：γe和γc分别为蒸发速率和冷凝速率；C为混合气体浓度；为气态水的摩尔分数，xsat为饱和水的摩尔分数.

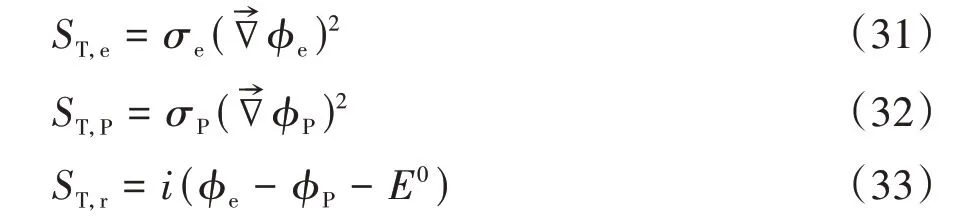
式中：σe为电子电导率；σP为质子电导率；ϕe为电子电势；ϕP为质子电势；i为电流密度；E0为等效电势.

1.6 边界条件

表2 总结了各个物理场的边界条件.该模型中所有的反应气体，假定均不能渗透过质子交换膜，且质子交换膜可以阻止所有的电子通过.在模型中，通过控制相对湿度来控制摩尔分数，其中相对湿度（RH）和摩尔分数的关系为：

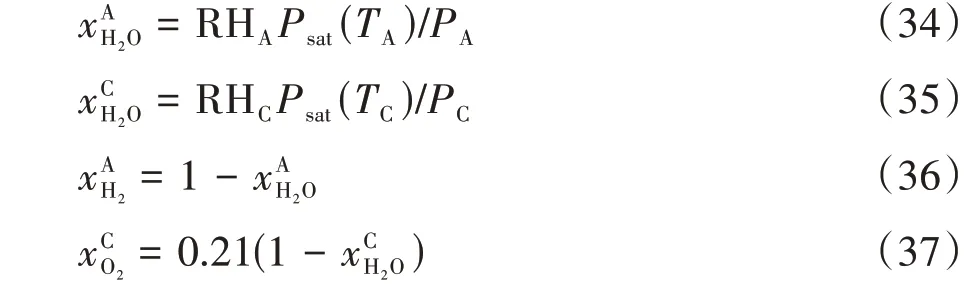
表2 边界条件Tab.2 Boundary Condition

2 结果和分析

2.1 模型验证

图3 所示的极化曲线，将实验数据和模型数据进行对比，本实验数据阳极和阴极在相同的工作条件下测得（阳极和阴极工作条件一样：压强=200 kPa、温度=353.15 K、相对湿度=80%），实验数据和模型仿真数据吻合良好，证明了该模型的合理性.本组实验的特征参数总结见表3.

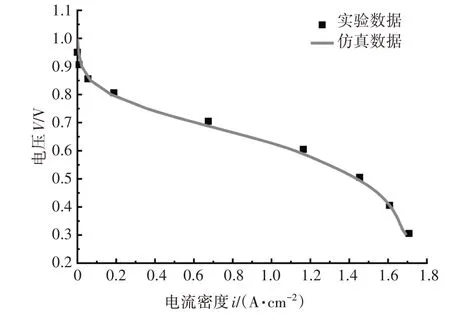
图3 燃料电池实验和仿真极化曲线对比Fig.3 Comparison of test results and simulation of fuel cell

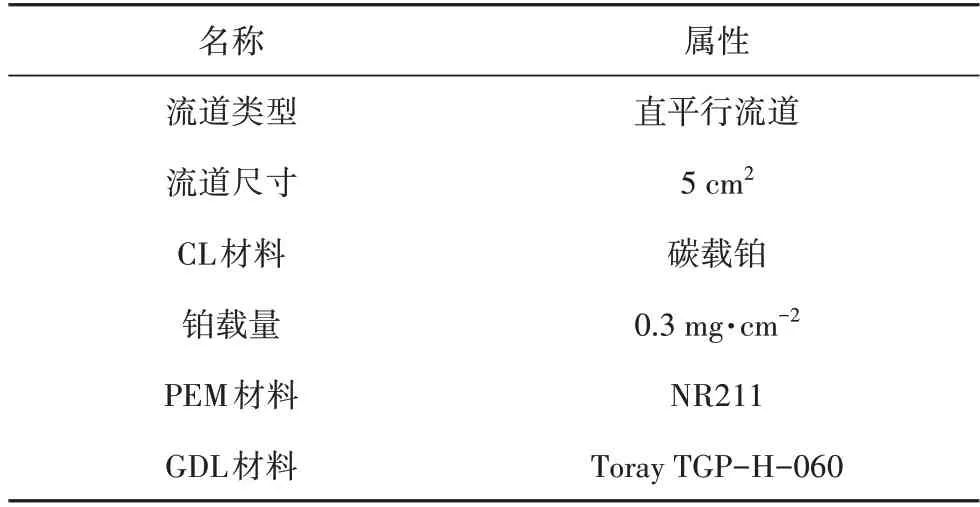
表3 实验特征参数Tab.3 Experimental characteristic parameters

2.2 PEM燃料电池的力学分析

图4 为PEM 燃料电池在受到装配力时，多孔介质的应力分布情况（文中图形结果仅为多孔介质区域）.从图4的应力分布可以发现：肋板下方的多孔介质受到的应力远大于流道下方的多孔介质，且流道下面的GDL 会产生入侵流道的现象.与此同时，在肋板和流道交界处下方的GDL有明显的应力集中现象，此处的应力值为多孔介质中的最大值5 MPa.图5 为燃料电池受到机械应力后的位移分布，从图中可以看出：由于肋板和BPP 直接接触，位于肋板下方GDL 的形变量要大于位于流道下方GDL 的形变量，流道下方GDL 的形变量几乎为0.MPL、CL 以及PEM的形变量相对于GDL的形变量而言是极小的.

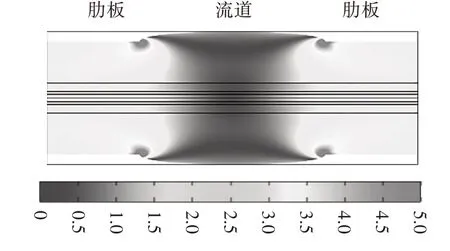
图4 应力分布（MPa）Fig.4 Stress distribution

图5 位移分布（μm）Fig.5 Displacement distribution

2.3 PEM燃料电池的温度分布

图6 为PEM 燃料电池在不同电流密度下（i=0.17 A∙cm-2、1.05 A∙cm-2、1.66 A∙cm-2）的温度分布.从图6 可以看出：流道下方多孔介质的温度高于肋板下方多孔介质的温度.由于机械压缩，肋板下方多孔介质的孔隙率相较于流道下方多孔介质的孔隙率要小，这样导致肋板下方的气体传输阻力要大于流道下方的气体传输阻力，从而使流道下方的多孔介质内部反应气体的浓度较高，相应的电化学反应产生的热量较多，温度也较高.还可以发现阴极的温度要高于阳极，这是由于在PEM燃料电池中，阳极和阴极是分别发生两个半电化学反应，阴极的还原反应的反应焓要大于阳极氧化反应的反应焓，所以阴极的温度要高于阳极的温度.随着电流密度的增加，电池内部的温度会增加，阳极和阴极的温差会随着电流密度的增加而增加.

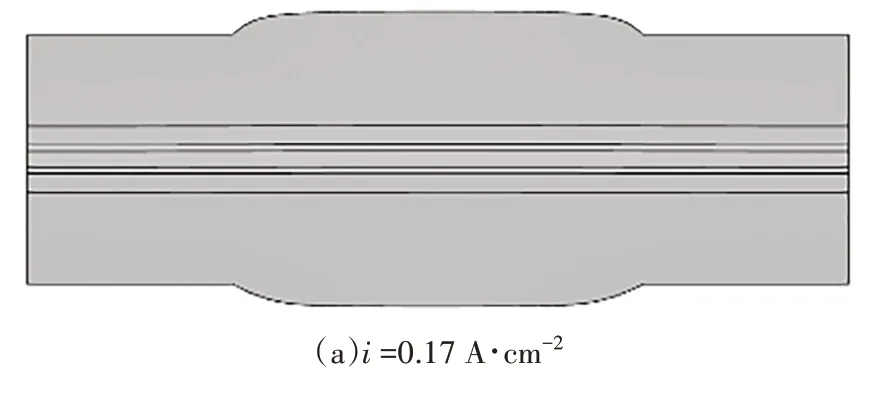
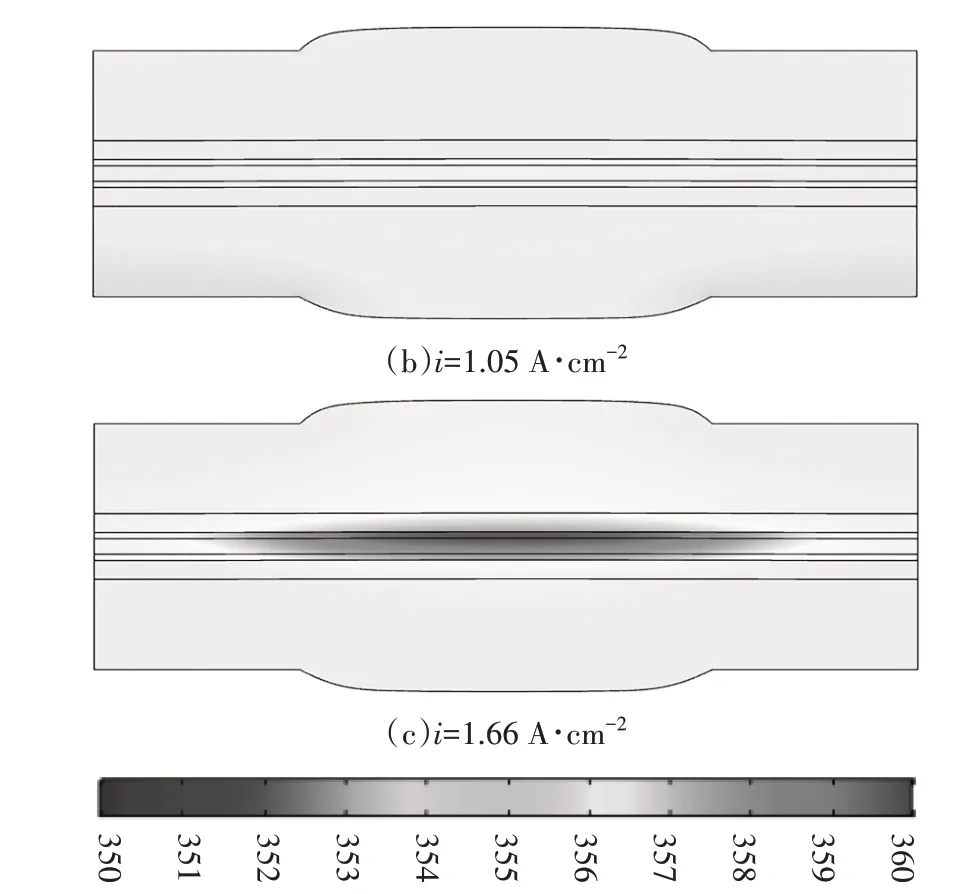
图6 不同电流密度的温度分布（K）Fig.6 Temperature distribution at different current density

2.4 PEM燃料电池的相对湿度分布

图7 是PEM 燃料电池在三个不同的电流密度下的（i=0.17 A∙cm-2、1.05 A∙cm-2、1.66 A∙cm-2）相对湿度分布.从图7（注：阳极和阴极的图例不同）可以发现：阴极的相对湿度随着电流密度的增加而逐渐增加，并且会超过1，尤其是在肋板下方的多孔介质区域增加明显.这是因为肋板下方的多孔介质在机械应力的作用下，传输参数如孔隙率和渗透率的减小，传输阻力的增大使得电化学产生的水不容易排出，加上肋板下方的多孔介质区域温度要低于流道下方的多孔介质区域温度，所以肋板下方区域的相对湿度要高于流道下方的.阳极的相对湿度分布则与阴极情况相反，阳极的相对湿度随着电流密度的增加而逐渐减小，且阳极的相对湿度均小于1.这是因为水的流通量是由电拖曳和反扩散两种因素共同决定的.随着电流密度的增加，电拖拽作用增强，阳极的水会随着质子向阴极流动，当电拖拽作用的流通量大于反扩散作用的流通量时，阳极内的水会随着电流密度的增加而减少.此外，阴极流道下方的水含量大于肋板下方的水含量，使得流道下方区域反扩散的作用大于肋板下方区域的反扩散作用，所以阳极流道下方的相对湿度大于肋板下方的相对湿度.随着电流密度的增加，CL 上的相对湿度首先在其两边变大，然后朝着CL 中间区域增加.当电流密度较小时，CL 中间区域的反应物浓度较高，使其中间区域温度较高，所以两边区域的相对湿度高于中间区域的相对湿度.当电流密度继续增加时，反应产生的水占了主导因素.因而，CL 中间区域的相对湿度随着水浓度的明显增加而变大.

图7 不同电流密度的相对湿度分布Fig.7 Relative humidity at different current density

2.5 PEM燃料电池液态水饱和度分布

从图7 可以看出：在不同电流密度的情况下，由于阳极的相对湿度均小于1，所以阳极一直没有液态水产生，故在图8 中没有绘制阳极液态水饱和度的分布.图8 是PEM 燃料电池在三个不同的电流密度下的（i=0.17 A∙cm-2、1.05 A∙cm-2、1.66 A∙cm-2）阴极液态水饱和度分布.阴极的相对湿度会在电流密度达到一定数值的时候大于1，此时会产生液态水.且阴极液态水饱和度随着电流密度的增加而逐渐增加［4，20］.当电流密度为1.66 A∙cm-2的时候，液态水饱和度可以达到0.3.液态水饱和度在肋板下方的多孔介质区域要大于流道下方，这是因为肋板下方的孔隙率和渗透率要小于流道下方的，所以产生的液态水更容易在肋板下方积累.且由于GDL 区域的温度要远小于CL 区域的温度，液态水饱和度的最大值会出现在肋板下方远离CL的GDL区域.

图8 不同电流密度的液体水饱和度分布Fig.8 Saturation at different current density

3 结论

本模型结合了机械应力和传热传质、电化学的多物理场模型求解气-液两相流，研究了机械应力下PEM 燃料电池的气-液两相流工作参数分布情况.本研究结论如下：

1）燃料电池在受到装配机械应力时，肋板下方的GDL 形变量最大，其他部件的形变量相对于GDL形变几乎可以忽略.肋板下方的多孔介质受到的机械应力要大于流道下方多孔介质受到的应力，且在肋板与流道交界处GDL有应力集中现象.

2）燃料电池阴极的温度要高于阳极，阴极CL的温度最高，随着电池的电流密度增加，电池的温度将增加，温差也会变大.当电流密度为1.66 A∙cm-2时，温差为10 K.

3）随着电流密度的增加，阴极的相对湿度从初始的0.8 增加到1.3，但阳极相对湿度从初始的0.8 减小到0.6左右.

4）阴极随着电流密度的增加会逐渐产生液态水，电流密度越大，液态水的饱和度越高.当电流密度为1.66 A∙cm-2时，饱和度为0.3.肋板下方多孔介质层中的液态水饱和度要大于流道下方的多孔介质层，且饱和度的最大值会发生在离肋板最近的GDL区域.