一种几何非线性低刚度高阻尼隔振器动态特性研究

刘国勇，郝鹏鹏，赵鹏鹏，刘海平

（1.北京科技大学机械工程学院，北京，100083；2.中科院微小卫星创新研究院，上海 201210）

常见的振动控制问题中，传统的振动控制方法一般基于线性理论，即期望更小的谐振频率与更低的谐振峰值来实现更好的隔振性能.但是，选择较小的谐振频率意味着较小的系统刚度，即系统的静态承载能力不足.以车辆的悬架系统为例，通常希望能在更低的频率、更宽的频带范围内实现良好的隔振，同时也要有一定的静承载力.而常见的线性常规隔振器由于其固有的局限性而无法满足这些隔振需求.因此，研究人员为了解决该类问题开发了多种悬架系统，如主动悬架系统.但是该类悬架系统存在系统复杂、可靠性不强等问题.

为了解决上述问题，近年来研究人员基于非线性动力学理论发现了一些新颖的隔振方法.这些隔振方法具有非常出色的隔振性能，尤其在宽频及低频范围内具有良好的隔振效果.

文献［1-3］利用水平弹簧产生的负刚度与垂向弹簧产生的正刚度相互抵消，从而实现准零刚度的机理，提出了一种准零刚度隔振器.但该隔振系统由于具有准零刚度的特性，在幅值较大的振动问题上存在严重的稳定性问题.此外，为了利用非线性准零刚度特性，文献［4］开发了准零刚度磁性弹簧系统.文献［5］研究了一种非线性磁性低频隔振器.文献［6］设计了一个带有弯曲梁的准零刚度隔振器.文献［7-9］设计了碟形橡胶准零刚度隔振器、屈曲板型准零刚度隔振器、气动可调式准零刚度隔振器.这些准零刚度隔振器可在不牺牲支撑能力的情况下降低整体动态刚度.但该类系统存在结构复杂、成本较高及可靠性不足等问题,推广应用受到了限制.

近年来，内含几何非线性X 型机构减隔振装置的研究得到了持续关注.文献［10-11］从仿生学角度提出采用X 型机构引入非线性阻尼，研究发现谐振振幅极大衰减，而在其他频段由于阻尼增大并未使系统响应传递特性变差.文献［12］将多层X 型机构与杠杆系统组合构成准零刚度隔振器，采用力控制可以有效调节系统反共振频率和低频范围的传递特性.文献［13］为了改善工人操作过程中所受恶劣力学环境的影响，创新性地提出采用多层X 型机构构建反共振隔振装置.研究表明，在保证设备正常负载条件下，反共振隔振装置可显著减小系统动态载荷的传递.文献［14］以航天器在轨非合作目标抓捕过程中周期或者冲击载荷作用下产生的微振动为控制目标，采用多层X 型机构建立机械臂和末端执行机构之间的隔振装置.研究表明，多层X 型机构组成的隔振装置可以有效控制自由悬浮状态卫星平台和被捕获目标之间的动态响应，且通过调整设计参数可以灵活调整其减隔振性能.文献［15］通过观察人体四肢运动过程中的力学关系，建立内含X 型机构的反共振隔振器模型.研究表明，此类反共振隔振器具备优良的低频宽频减隔振性能.文献［16］提出采用受拉伸载荷作用的X 型机构建立准零刚度隔振装置.研究表明，在被动振动控制中采用结构非线性的设计方法，X 型机构可以将非常有益的非线性引入隔振系统，从而产生高静态-低动态刚度的隔振特性［17-19］.但是，在隔振系统研究中，该团队研究较多的是空气阻尼、机构间的旋转摩擦阻尼及引入惯性系统所产生的非线性阻尼,并未在X型机构内部引入阻尼单元,更谈不上研究其几何非线性的阻尼放大特性.

综上，本文基于X 型机构可实现对阻尼系数放大和多层X 型机构可实现隔振系统动态刚度减小的机理，提出一种可实现低动态刚度与高阻尼隔振性能的隔振器，并通过合理设计结构参数可使其拥有较高的负载能力；同时该隔振系统具有结构简单、可靠性高、适用性强、使用灵活、易于制造和实施等优点.

1 动力学建模

低刚度高阻尼隔振器的力学模型如图1 所示.其中，图1（a）为隔振系统的初始状态，图1（b）为在激励力作用下的平衡状态.M为惯性质量；k为弹簧刚度；c为阻尼系数；l1为上部X 型机构单根刚性杆的长度，l2为下部X 型机构单根刚性杆的长度；四根刚性杆两两铰接，刚性杆与水平轴y的初始夹角为θ；运动前后，初始夹角θ的变化量为φ；t为时间；y1为上部X 型机构在受激励力作用下水平方向的单边变形量；y3为下部X型机构在受激励力作用下水平方向的单边变形量；x1为上部X型机构在受激励力作用下垂直方向的总变形量；x2为下部X型机构在受激励力作用下垂直方向的总变形量，F为激励力.假设，垂直方向向上为x轴正方向，水平方向向右为y轴正方向.

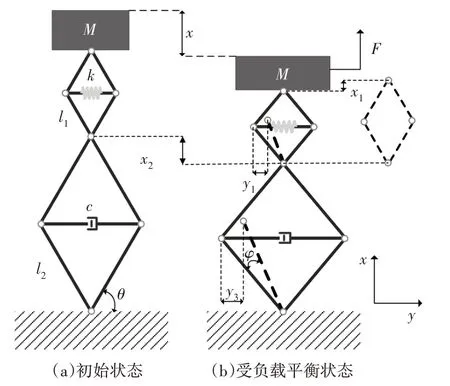
图1 力学模型Fig.1 Mechanical model

根据图1所示X型机构的几何运动关系，得到：

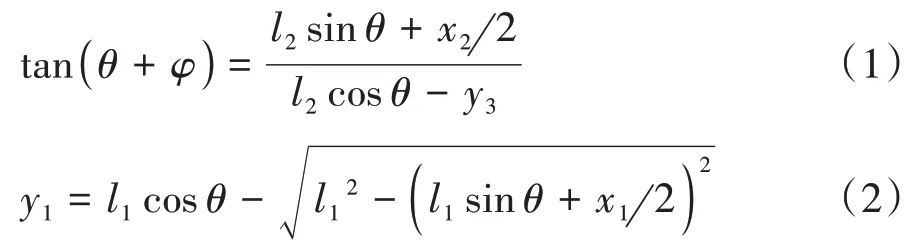
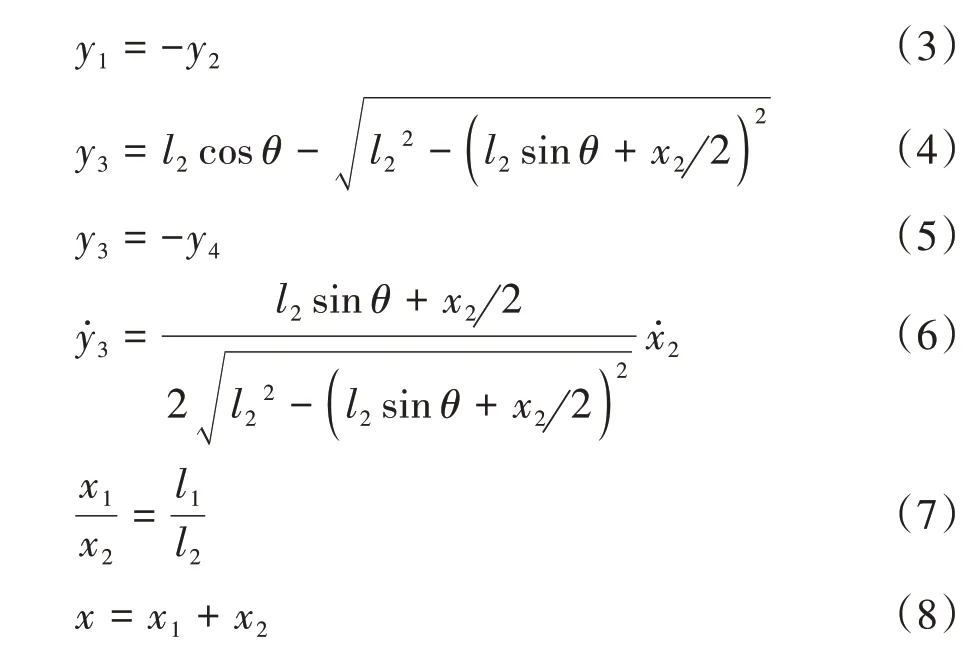
式中：x为惯性质量的垂向位移；y1和y2分别为上部X型机构刚性杆活动铰接点的水平位移（y1和y2反向）；y3和y4分别为下部X 型机构刚性杆活动铰接点的水平位移（y3和y4反向）；和则为下部X 型机构刚性杆活动铰接点的水平速度.

可以得到隔振系统的动能为：

隔振系统的弹性势能可表示为：

则可得到隔振系统的拉格朗日函数为：

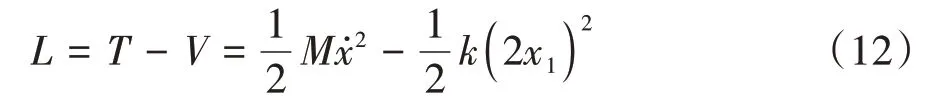
根据拉格朗日定理，可得到：

假设基础所受激励为F=F0cosωt，则该隔振系统的运动微分方程可表示为：

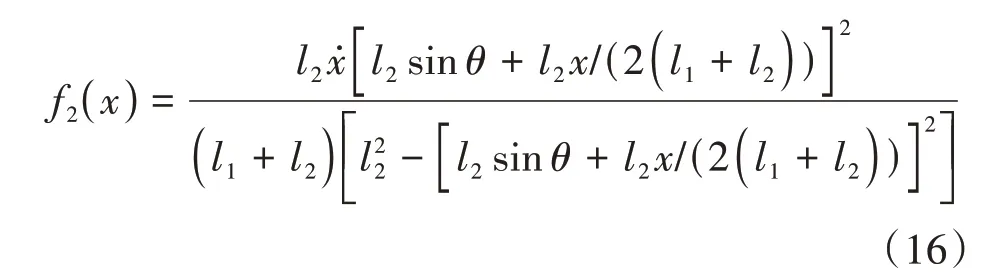
由于函数f1（x）和f2（x）在x=0 处连续，将式（15）和式（16）分别在零平衡位置采用三阶泰勒级数展开，可得：

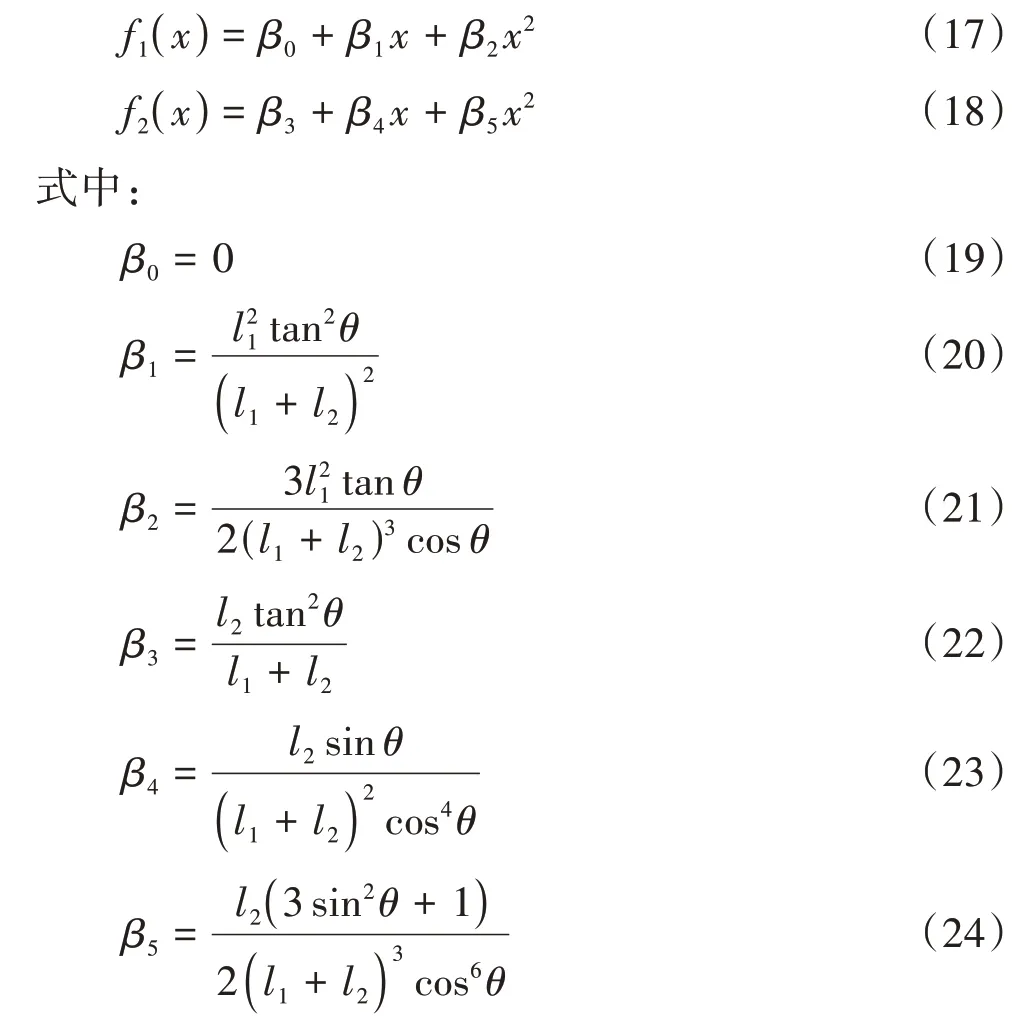
将式（17）和式（18）代入式（14）中，可得：

为了方便计算，对式（25）引入无量纲参数，具体定义如下：

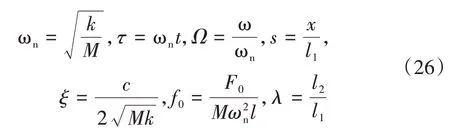
式中：ωn为隔振系统固有频率；τ为无量纲时间；Ω为频率比；s为无量纲位移；ξ为阻尼比；f0为无量纲激励力幅值；λ为杆长比.

进而得到：

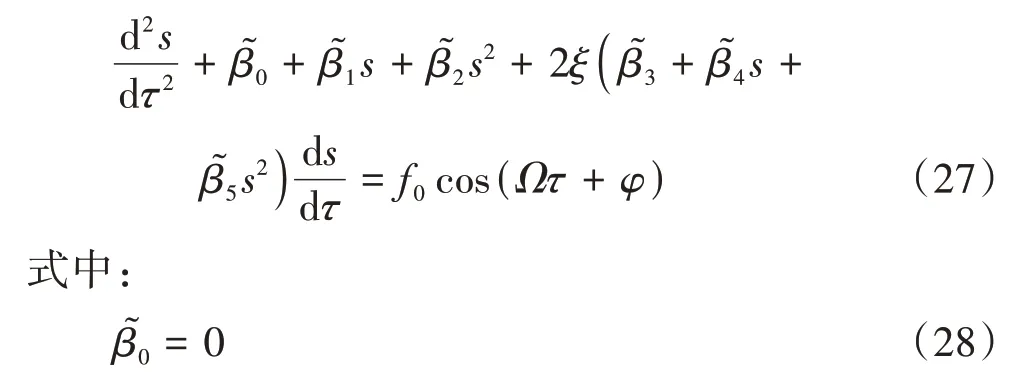
采用谐波平衡法对式（27）进行求解.假设其稳态解的形式为：

式中：s0为位移幅值.

将式（34）代入式（27）并略掉高次项得：

为了方便表示，定义：

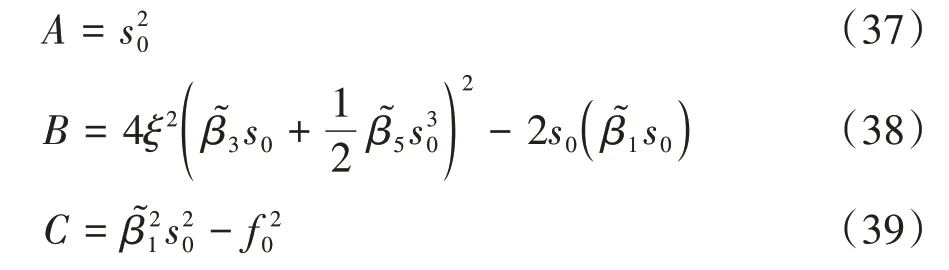
解得力激励条件下隔振系统的幅频响应和相频响应：

式中：Ω的上标代表力激励，下标则表示组成幅频响应曲线的两个部分.

2 等效刚度系数和等效阻尼系数

2.1 等效刚度系数分析

由前节动力学建模过程分析可知，低刚度高阻尼隔振系统的等效弹性恢复力为：

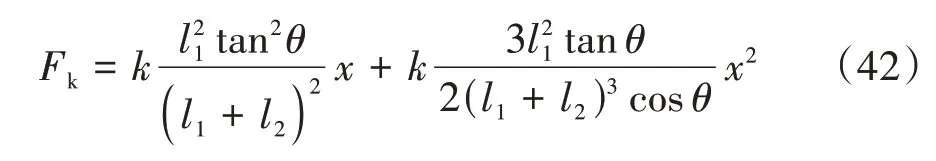
式（42）对x进行求导并无量纲化后即可解得系统的等效刚度系数：

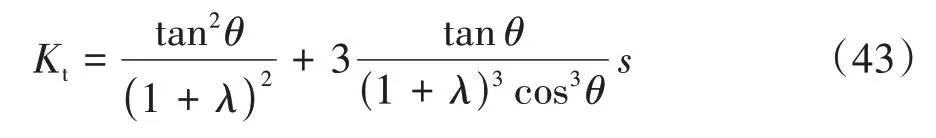
式中：Kt即为低刚度高阻尼隔振系统的无量纲化等效刚度系数.暂定λ=3，θ=60°，由式（43）即可画出无量纲化等效刚度系数随无量纲位移的变化规律，如图2所示.

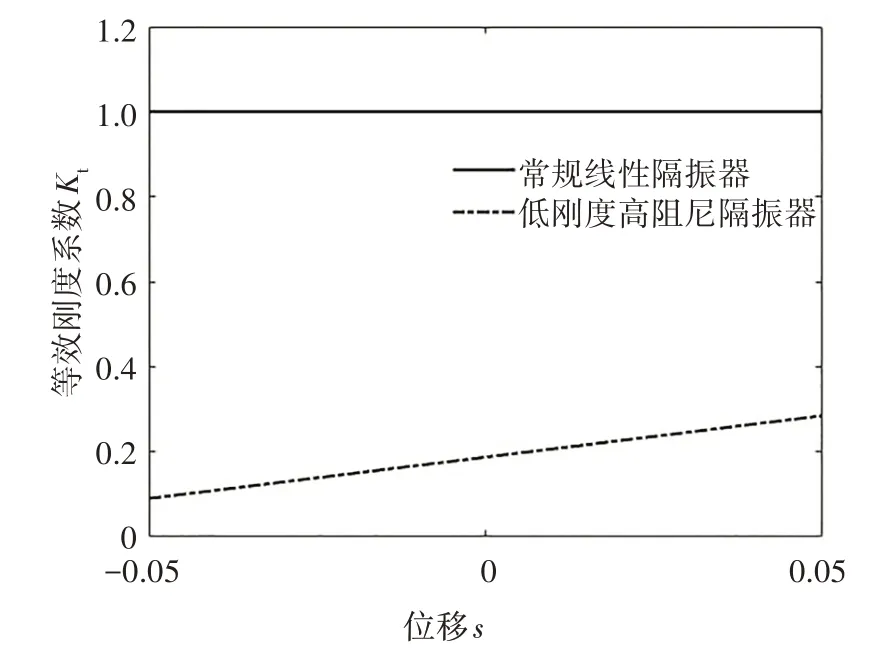
图2 无量纲等效刚度系数Fig.2 Equivalent stiffness coefficient

由图2 可以看出，与常规线性隔振系统相比，低刚度高阻尼隔振系统的等效刚度系数明显减小，证明该隔振器实现了低刚度的设计目标.

2.2 等效阻尼系数分析

与常规线性隔振系统类似，低刚度高阻尼隔振系统的等效阻尼恢复力为：

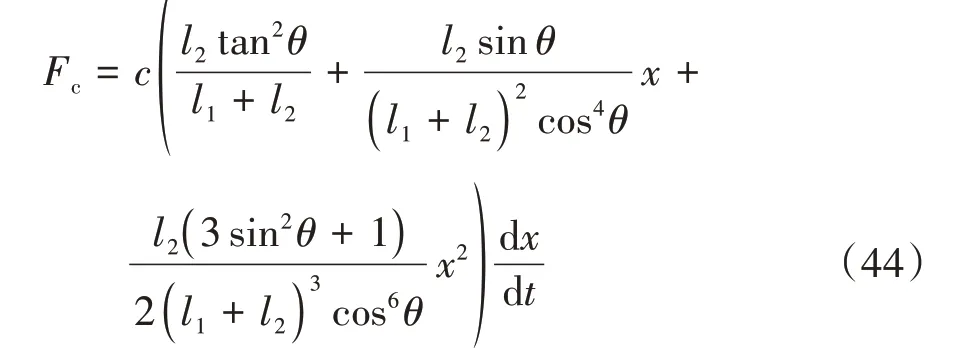
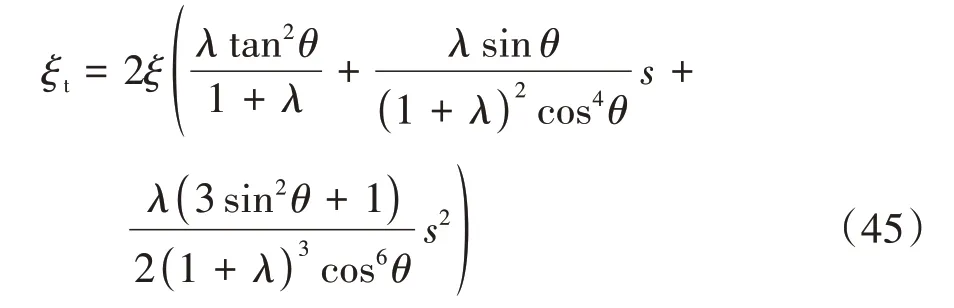
式中：ξt为低刚度高阻尼隔振器的等效阻尼系数.由式（45）即可给出隔振系统等效阻尼系数随s的变化规律，如图3所示.

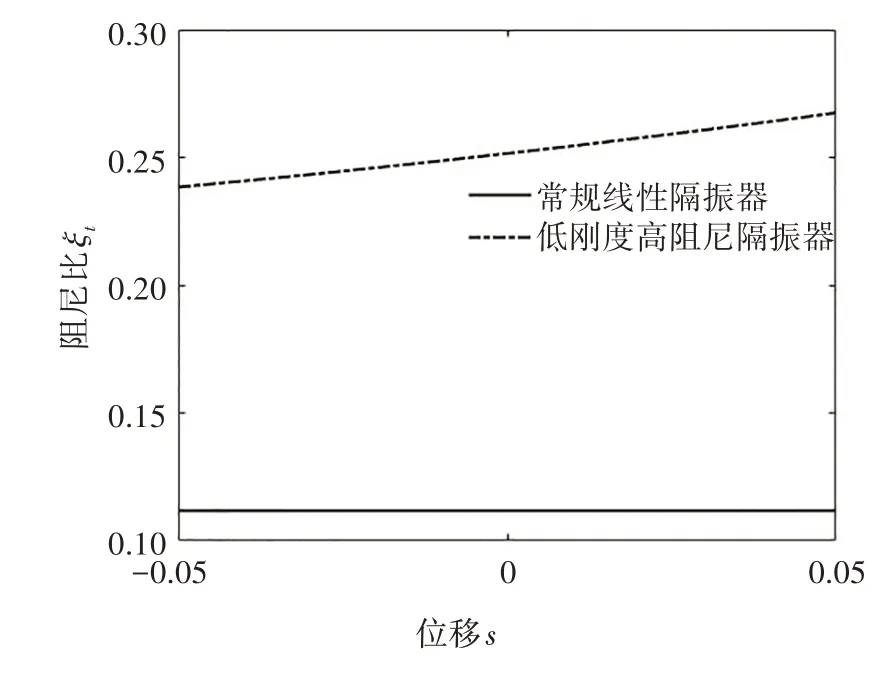
图3 无量纲等效阻尼系数Fig.3 Equivalent damping coefficient

由图3 可以看出，在当前结构参数下，无量纲等效阻尼系数放大了约2 倍.因此，与常规线性隔振系统相比，低刚度高阻尼隔振系统的阻尼得到了显著放大.

综上，选择合适的参数，低刚度高阻尼隔振系统的等效阻尼得到显著放大的同时，隔振系统刚度显著减小.

3 隔振效果评估

为验证低刚度高阻尼隔振器的隔振效果，与常规线性隔振器、准零刚度隔振器进行对比.

对于常规线性隔振器，容易得到力传递率为：

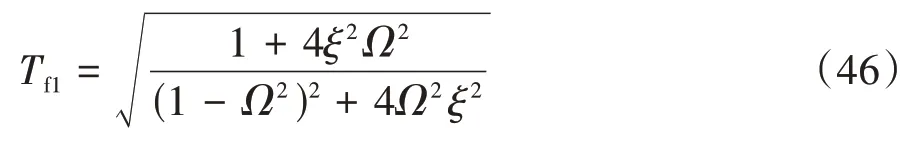
对于准零刚度隔振器［1-3］，其运动微分方程为：

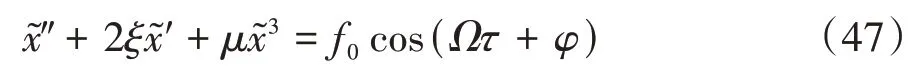
其力传递率可表示为：

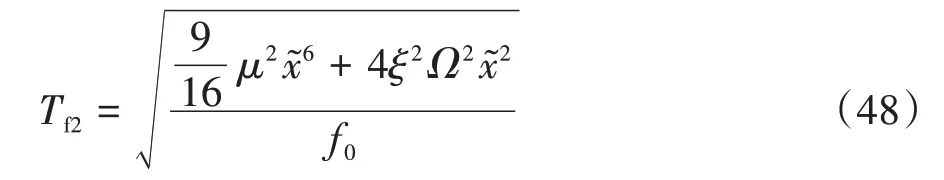
而对于低刚度高阻尼隔振器传递到基础的力可由谐波叠加的方式求得：

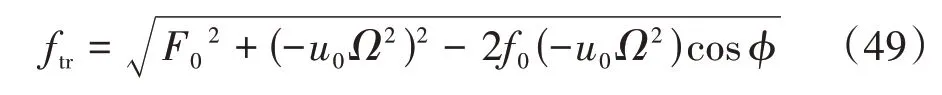
得到低刚度高阻尼隔振器的力传递率为：

由式（50）可得低刚度高阻尼隔振器的力传递率曲线Ω-T.同时，为了验证含放大机构隔振器解析解的正确性，利用龙格-库塔法给出部分频点的时域解.

低刚度高阻尼隔振器的初始设计参数为ξ=0.05，θ=60°，λ=3.分别得到常规线性隔振器、准零刚度隔振器与低刚度高阻尼隔振器的力传递率曲线；同时给出数值计算结果，如图4所示.

图4 不同隔振器力传递率曲线Fig.4 Force transmissibility curves for different isolators

由图4 可见，低刚度高阻尼隔振器的数值解和解析结果良好一致，证明其频域解析结果有效.

与常规线性隔振器相比，力传递率曲线峰值得到显著衰减，且峰值频率向低频移动，即有着更宽的隔振频带.

与准零刚度隔振器相比，本文所述低刚度高阻尼隔振器具有以下优点.

1）由于多稳态非线性的出现，准零刚度隔振器会出现严重的稳定性问题，而对低刚度高阻尼隔振器而言，其传递率曲线表现出较弱的非线性且没有分岔、混沌及多稳态现象，因此该隔振器有着较好的稳定性.

2）准零刚度隔振器只有在其隔振频率远大于跳变频率时才可实现较为安全的隔振，相比之下，低刚度高阻尼隔振器具有更宽的隔振频带.

3）在不改变刚度系数及阻尼系数的情况下，低刚度高阻尼隔振器通过其系统参数的调整可实现比准零刚度隔振器更低的谐振频率及更低的谐振峰值.

此外，由式（43）可以看出，系统的等效刚度随着初始倾角的增大而增大，因此本文所述低刚度高阻尼隔振器的静承载能力可根据隔振器结构的设计参数进行调节，从而实现“高静低动”的效果.如在负载质量未作用于隔振器时，设计初始倾角为一较大值，此时隔振器的等效刚度较大，可以保证隔振系统有较好的静承载能力；当负载作用在隔振器上且达到静平衡状态时，隔振系统的初始倾角必然会减小，此时隔振系统的等效刚度也会减小，即可保证该隔振器有较小的动刚度.

由此说明，低刚度高阻尼隔振器可实现对动刚度减小和阻尼放大的设计目标，即在系统动态刚度减小的同时实现了高阻尼输出，并且有着较好的稳定性与静承载能力.

4 有限元模型验证

为了验证解析模型的正确性，现建立与解析模型等效的有限元模型，如图5和图6所示.其中，惯性质量点的值M=10 kg；杆长比λ=3；初始倾角θ=60°；弹簧刚度k=2 000 N/m；阻尼系数c=10 N/m.

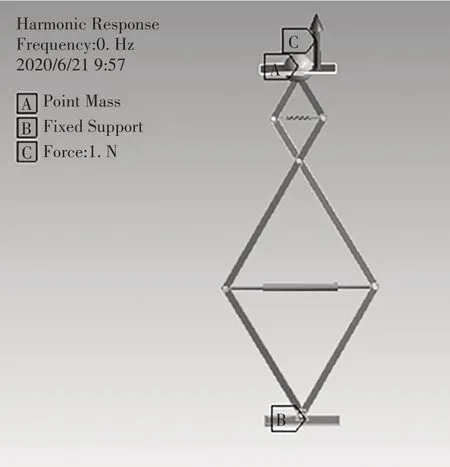
图5 几何模型Fig.5 Geometric model

图6 网格模型Fig.6 Mesh model

边界条件：杆之间铰接通过图示的轴采用revo⁃lute连接方式实现；在上部X 型机构内部添加刚度单元，在下部X 型机构内部添加阻尼单元，分别表征理论模型中的刚度单元与阻尼单元.在上板中心位置添加质量点表征负载；下板采用Fixed support固支表征基础；在上板施加垂向正弦力激励，表征力激励.网格条件为：所有网格单元均采用六面体网格，网格单元尺寸为3 mm，共划分为4 380 个单元，22 143 个节点.

上述分析在Ansys workbench扫频分析模块中进行，设置扫频范围为0～100 Hz，计算频点数为300个.通过提取固支端的反力得到激励力通过隔振器传递到基础的力，从而得到传递率曲线，如图7所示.

由图7 可以看出：有限元分析所得传递率曲线与解析方法所得传递率曲线在高频处有略微的差别，这是由有限元模型的高频局部模态引起的，由于隔振系统解析结果主要用于表征系统在中低频段的减隔振效果，不包含高频模态的影响，所以本文中由高频局部模态引起的动态响应不再讨论.由于刚性杆的质量相对于质量点较小，对有限元分析结果影响不大，因此两条传递率曲线基本完全拟合，由此说明解析结果正确、有效.

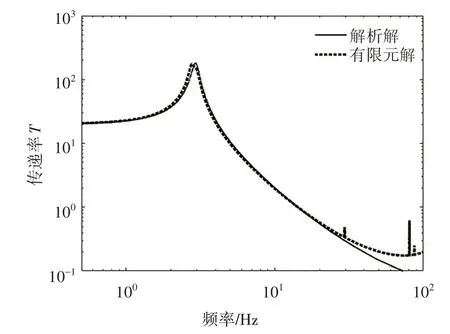
图7 有限元结果与解析结果对比Fig.7 Comparison of finite element results and analytical results

5 参数影响分析

根据第1 节所述内容，低刚度高阻尼隔振器的主要设计参数为λ、θ和ξ，以下重点讨论这些设计参数对低刚度高阻尼隔振器动态特性的影响.此外，还分析了激励力幅值对隔振器传递率的影响.为了便于讨论，以第3节中定义的设计参数为初始值.

5.1 阻尼比ξ对隔振性能的影响

阻尼比分别取ξ为0.01、0.05、0.10，得到力传递率曲线，如图8 所示.由图可见，阻尼系数主要对力传递峰值有影响，即随着阻尼比增大，力传递率峰值显著减小.

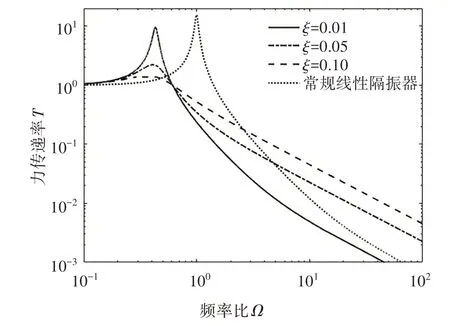
图8 不同阻尼比对应的力传递率Fig.8 Force transmissibility curves for different damping ratios

5.2 杆长比λ对隔振性能的影响

低刚度高阻尼隔振器杆长比对力传递率曲线的影响如图9 所示.其中，杆长比λ的取值分别为1、3和5.可见，杆长比增大，力传递率谐振峰值明显减小；其谐振频率向低频移动.由此可说明，杆长比越大，系统刚度越小，系统阻尼越大.

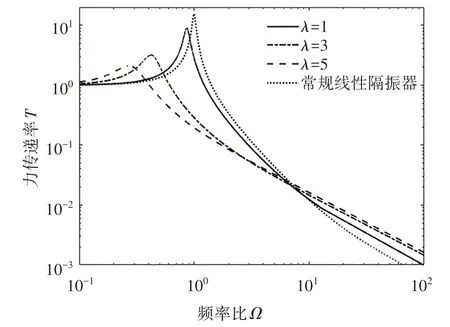
图9 不同杆长比对应的力传递Fig.9 Force transmissibility curves for different rod length ratios

5.3 初始倾角值θ对隔振性能的影响

低刚度高阻尼隔振器铰接杆初始倾角θ对力传递率的影响如图10 所示.由图10 可见，初始倾角分别为45°、60°和70°时，随着初始倾角增大，力传递率曲线谐振峰值明显减小，同时其谐振频率向高频移动.由此可说明，随着初始倾角的增大，系统阻尼在增大的同时，系统刚度也在增大.因此，为了实现隔振器低刚度高阻尼的输出这个设计目标，初始角度需要根据具体设计参数进行调整.

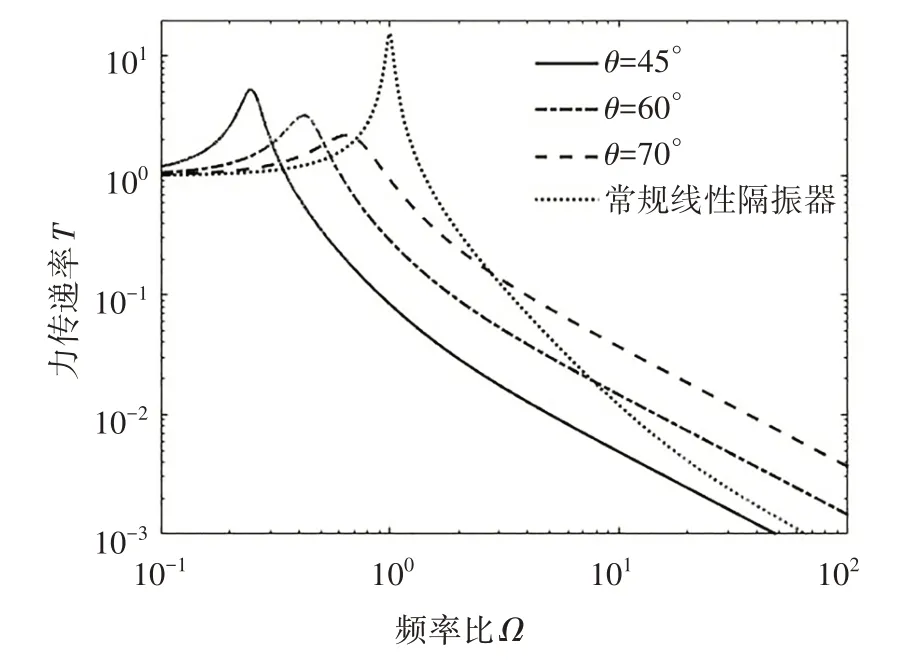
图10 不同初始倾角值对应的力传递率Fig.10 Force transmissibility curves for different initial inclination values

5.4 激励力幅值F对隔振性能的影响

低刚度高阻尼隔振器激励力幅值对力传递率的影响如图11 所示.由图11 可见，随着激励力幅值的增大，谐振幅值在减小，但其减小效果极其微小，而谐振频率基本没有变化.由此可说明激励力幅值对隔振效果的影响较小，也说明该隔振系统的非线性特性较弱.这就导致F=1 N、5 N、10 N 的3条力传递率曲线基本重合，因此图11看起来只有2条曲线.

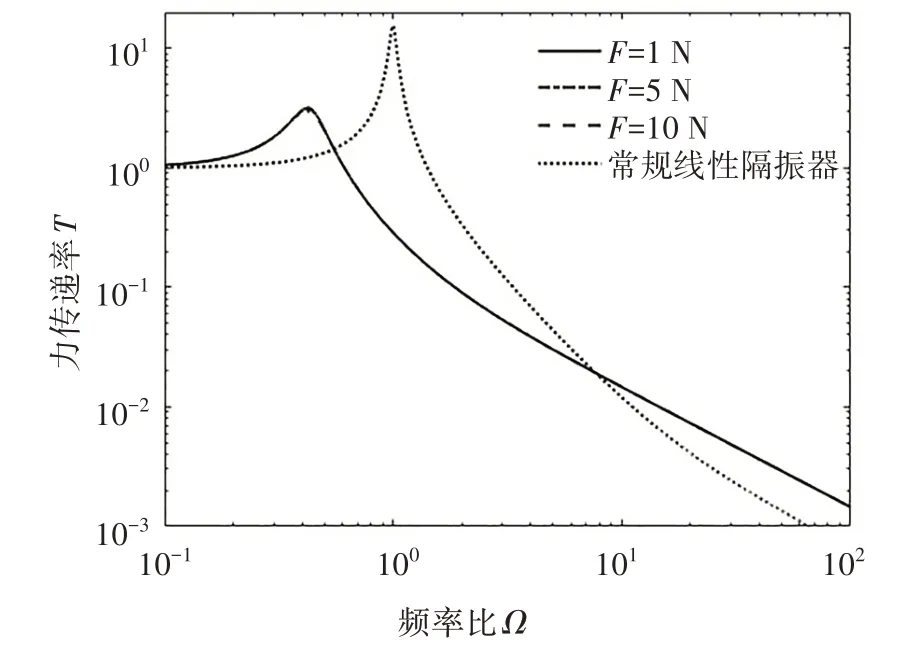
图11 不同激励幅值对应的力传递率Fig.11 Force transmissibility curves for different excitation amplitudes

6 结论

本文提出一种低刚度高阻尼的隔振器.首先，在所建隔振系统动力学方程的基础上，采用谐波平衡法给出其幅频响应和相频响应的解析表达式，并进行了验证，同时分别给出该隔振系统的等效刚度和等效阻尼表达式.其次，求得并利用有限元模型验证了隔振系统的力传递率，同时在频域对隔振器隔振效果进行了评估.最后，采用力传递率作为评价指标，对其关键设计参数进行了影响研究.研究结果表明：

1）与常规线性隔振器相比，低刚度高阻尼隔振系统的力传递率曲线峰值显著衰减，且谐振频率向低频移动.

2）与准零刚度隔振器相比，低刚度高阻尼隔振器有着较好的稳定性、更宽的隔振频带，隔振性能可通过结构设计参数灵活调整.

3）数值解与解析解的对比验证及有限元模型验证，证明所建解析模型和表达式正确有效.

4）隔振系统设计参数对隔振性能均有较大影响：隔振器阻尼比增大，力传递率峰值减小，谐振频率基本没有变化；杆长比增大，力传递率谐振峰值明显减小；其谐振频率向低频移动；初始倾角θ增大，力传递率曲线谐振峰值明显减小，同时其谐振频率向高频移动；合理设计结构参数，隔振器可实现“高静低动”的隔振特性.

本文研究成果对X 型机构类型隔振器的设计和应用具有一定的理论指导意义.