轨道交通新型正交异性钢桥面板局部应力分析*

曾勇 薛晓芳 张路 敖付勇

1.重庆交通大学山区桥梁及隧道工程国家重点实验室 400074 2.重庆交通大学山区桥梁结构与材料教育部工程研究中心 400074 3.重庆市轨道交通（集团）有限公司 401121

引言

轨道车辆在通过桥梁过程中，正交异性桥面板局部位置不但要直接承受车辆轮载的竖向压力，还要作为纵横梁上翼缘传递剪力弯矩，同时伴随着车辆移动，力的大小还在随时间变化，使其处于复杂的时变三轴应力状态。正交异性钢桥面板的受力问题是一个相当复杂的问题［1，2］。

赵欣欣［3］等根据正交异性板形式变化，对10年来我国关于正交异性板设计和结构构造细节的研究情况进行了综述分析。张清华［4］等人以港珠澳大桥为背景，分析了新型超高性能混凝土正交异性组合桥面板的受力情况，并将其与传统的正交异性板进行了比较。叶华文［5］等以某公轨两用单索面斜拉桥为研究对象，开展疲劳试验，以评估正交异性板设计参数的合理性。祝志文［6］等为了研究弧形切口处的细节，以某桥为研究背景，通过在现场监测随机的车流量并利用循环计数方法得到弧形切口处的应力谱。曾勇［7］等为了研究在循环往复荷载作用下正交异性板的关键细节处易开裂这一问题，以某悬索桥为工程背景，进行了1:2 的缩尺大节段模型疲劳试验。童乐为［8］等对正交异性钢桥面板的结构分析、疲劳强度、桥梁荷载谱等疲劳验算进行了系统化研究。袁卓亚［9］等将实验和有限元分析相结合，对正交异性钢桥面板的应力分布情况进行了研究。

轨道交通桥梁与公路桥梁有很大的不同，轨道车辆轴重大，冲击力强，正交异性钢桥面板结构的受力行为与公路桥梁存在差异，现行的钢结构规范有关疲劳的内容与现有的公轨两用桥梁或轨道专用桥梁不尽吻合，因此对轨道交通正交异性桥面板展开受力研究是很有必要的。虽然单一的开口肋正交异性钢桥面板和闭口的U肋正交异性钢桥面板有较多的研究，但是同时含有开口T肋与闭口U肋的正交异性钢桥面板的研究还相对较少。

本文通过建立某桥的正交异性钢桥面板模型，对其疲劳焊缝进行了受力分析，研究应力场分布特征，为此类桥面板结构的设计和评估提供参考依据。

1 工程概况

某轨道交通桥梁是国内轨道交通专用桥中跨径最大的斜拉桥，大桥总长为594m，其中中跨长340m，全宽19.6m。在该桥桥面板钢轨下方放置两道高796mm、厚20mm的倒T形纵梁；其他纵向加劲肋采用U 型加劲肋，上部宽300mm，下部宽180mm，厚8mm；为了加强桥面板的刚度，每3m放置一道12mm 厚的横隔板。轨道交通桥梁钢箱梁断面布置及开孔尺寸见图1、图2。该桥的正交异性钢桥面板同时含有开口T肋与闭口与U 肋，结构复杂，结构形式有一定的特殊性。

图1 城市轨道交通桥梁钢梁截面布置（单位： mm）Fig.1 Layout of steel girder s cross section a bridge in urban rail transit（unit：mm）

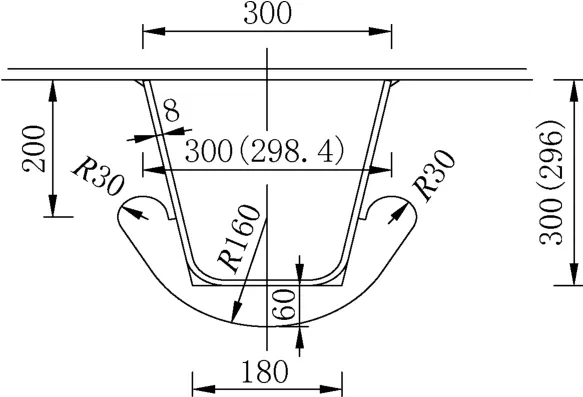
图2 横隔板开孔形式（单位： mm）Fig.2 Diaphragm opening type（unit：mm）

在传统的正交异性钢桥面板分析方法中，主要将其分为三个结构体系，其中主梁体系的内力变化幅趋于恒定，对于焊接钢结构的疲劳主要是通过应力幅进行计算，因此主梁体系的影响可以忽略。本文主要研究桥面体系，为了模型的计算精度，提高计算效率，同时保证受力与原桥相同，参照纵向加劲肋处开孔以上高度与横隔板总高之比不能超过0.4 这一规定，截取钢箱梁顶板以及顶板下900mm 建立有限元模型，其中纵向截取跨中箱梁段12m，包含4 道横隔板，间距为3m，横桥向取6.2m，包含9 个U 肋和两根倒T纵梁，两个U 肋中心线之间的距离为0.6m，倒T纵梁与U肋中心线距离为0.45m。

2 有限元计算模型

2.1 模型概述

模型采用大型有限元软件ANSYS 进行建立，由于桥面板、横隔板和纵肋在使用过程中都处于弹性阶段并且都是薄板，所以用板壳单元SHELL63 来建模分析。SHELL63 单元具有弯曲和薄膜两种功能，该单元有4 个节点，允许面内荷载和法向荷载，可以很好地模拟钢桥面板的几何特性和应力特性［10］。模型采用钢材的弹性模量E ＝2.1 × 1011Pa，泊松比μ ＝0.3，密度为7850kg／m3，在选取的节段横隔板两端施加固定约束，顺桥向两端允许有竖向位移而没有水平位移。模型如图3 所示。

图3 轨道交通正交异性钢桥面板简化模型Fig.3 Simplified model of orthotropic steel deck slab of rail transit

2.2 加载力的确定

根据轨道交通桥梁特点，轨道车辆都是在固定的轨道上行驶，设计时将轨道布置在2 根倒T纵梁之上。关于荷载在无道砟桥面上的横向纵向分布，根据《城市轨道交通桥梁设计规范》（GB／T 51234—2017）中的规定，在纵桥向上列车的轴重引起的集中荷载可分布于三个钢轨支点之上，在横桥向上列车轴重引起的集中荷载宜按轨底宽度加两倍的轨下基础高度进行计算。本次选取等效轴重最大的地铁A 型车作为加载。轴重荷载纵、横向分布见图4。图中：Qvi为列车轴重引起的集中力；a为钢轨支点间距。

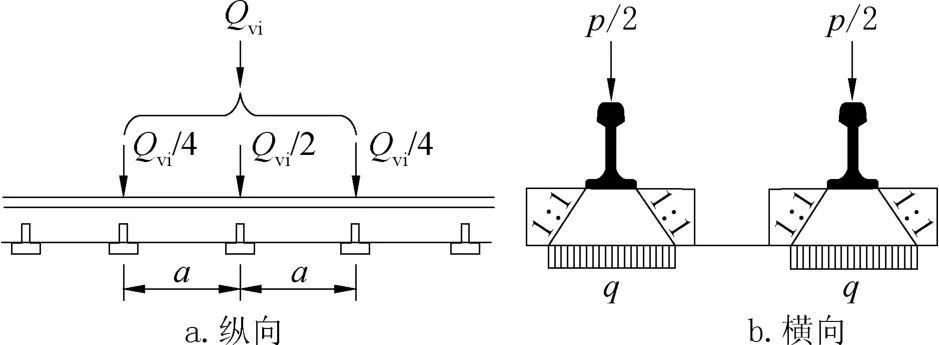
图4 轴重荷载分布Fig.4 Transverse distribution of axle load

在规范中给出了轴重荷载在横向上的均布分布形式，在纵向上只给出了集中荷载的分布形式，其均布分布形式参考美国钢结构设计手册的有关规定，认为轴力在纵桥向上均匀分布的长度可取0.925m再加上轨枕板的厚度。根据轨道交通桥梁设计参数，两钢轨支点之间的距离a ＝0.6m，轨底宽度为0.3m，轨枕板厚度为0.284m，计算得出在纵桥上的分布长度为1.209m，与两钢轨支点间距相近，可直接取1.2m。本文按单轴荷载分析正交异性板的应力分布情况，确定出各个疲劳焊缝的最不利加载位置，然后比较分析双轴荷载作用与单轴荷载作用对各个疲劳焊缝的影响。

2.3 最不利加载位置的确定

根据轨道交通桥梁的设计参数，计算可得单个车轮的轮压荷载面积为（1200 ×882）mm2，具体加载位置如图5 所示。为了模拟车轮在桥面板上移动，确定最不利加载位置，轮压荷载在纵桥向以倒T纵梁为荷载中心，从第一道横隔板开始移动至最后一道横隔板，每0.75m移动一次，共计13 个工况。本文主要为了研究正交异性钢桥面板的疲劳分析，因此只考虑了结构第二受力体系，而没有考虑第一受力体系，且模型为节段模型，限于篇幅只按纵向单独工况加载。加载位置见图6。

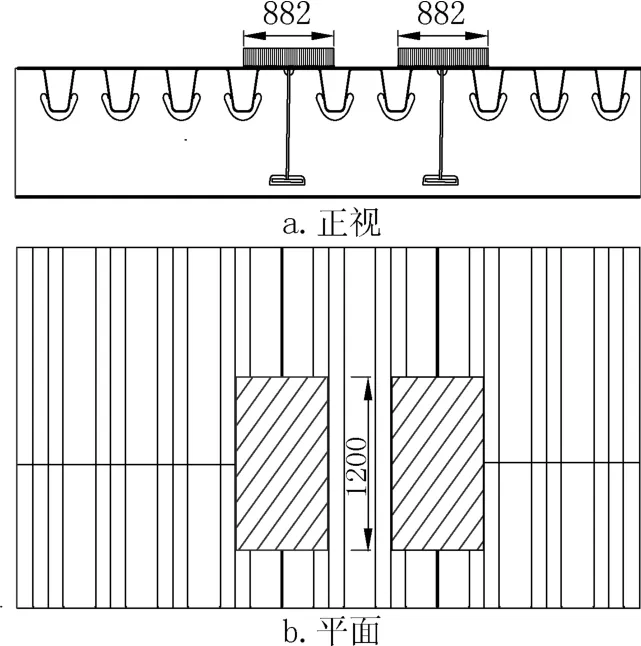
图5 单轴荷载加载位置（单位： mm）Fig.5 Plan of loading position of uniaxial load（unit：mm）

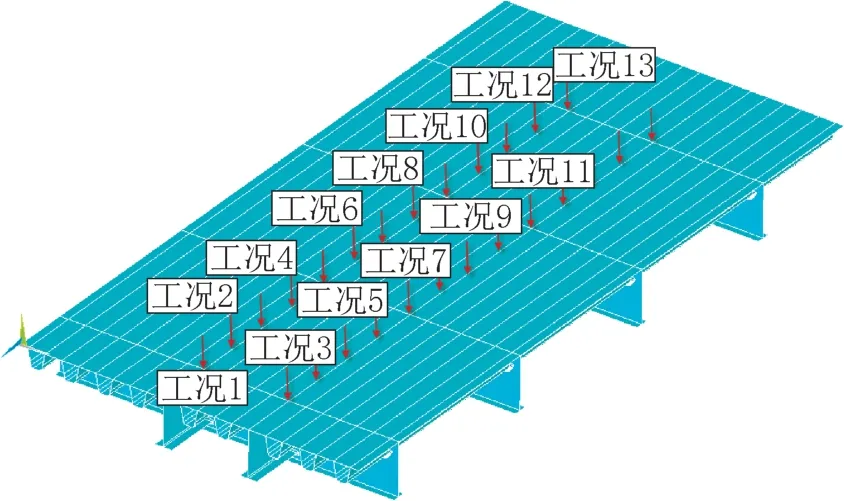
图6 模型加载位置示意Fig.6 Schematic diagram of loading position of model

根据有限元分析的应力分布情况，选取以下几个位置点进行重点分析，如图7 所示。其中关注点①为桥面板下表面；关注点②为横隔板开孔边缘位置；关注点③为横隔板与U 肋连接位置，关注点④为U肋与桥面板连接位置。

图7 关键应力点的提取位置Fig.7 Extraction position of key stress points

3 计算结果及分析

3.1 桥面板应力分布情况

通过有限元分析，对13 种工况加载位置下方的桥面板下表面应力进行计算，提取关注点①对应的桥面板下表面的应力，其在纵桥向上的计算位置对应每个加载工况。每个计算位置都有对应的最不利加载工况，即加载中心位于该计算位置之上，计算位置如图8 所示。

图8 应力提取位置Fig.8 Location of stress extraction

计算结果表明，桥面板的下表面在纵、横方向上具有相似的应力分布规律：

（1）当加载工况位于有横隔板支撑的桥面板上方时（工况1、工况5、工况9、工况13），桥面板下表面所受的横向应力与纵向应力最大值均出现在工况对应计算位置的横隔板与桥面板连接处。在工况5作用下，计算位置3处的桥面板下表面横、纵向应力均为最大值，分别为－14.89MPa、－5.86MPa。

（2）当加载工况位于两横隔板中间的桥面板上方时（工况3、工况7、工况11），与之相邻的两个横隔板桥面板下表面的横向应力值大于各个工况所对应计算处的横向应力值，最大的纵向应力值则出现在各个工况所对应计算位置。当加载工况位于桥面板一般位置时（工况2、工况4、工况6、工况8、工况10、工况12），应力分布规律与在两横隔板中间加载相似，说明影响应力分布只与加载位置是否位于横隔板上方有关。

（3）当单轴荷载作用在桥面板时，应力影响范围较小，在加载位置下方应力值较大，超过一定范围后应力迅速下降，应力集中现象明显。

桥面板下表面各个计算点在各自最不利受力情况的横向应力与纵向应力如图9 所示。根据此图可以得到桥面板下表面横向应力值在整体上要比纵向大这一结论。在有横隔板支撑位置加载时桥面板应力值较大，在一般位置加载时桥面板应力值较小，这一规律，横向应力与纵向应力相同，且最大应力值均出现在第二横隔板支撑的桥面板位置，对应工况5。依此可以推定，桥面板与横隔板连接位置非常容易产生应力集中现象。

图9 桥面板最不利工况下的横向及纵向应力Fig.9 Transverse and longitudinal stress of bridge deck under the most unfavorable condition

3.2 横隔板应力分布情况

正交异性钢桥面板钢桥面板纵肋与横隔板相交部位应力集中，为了降低该部位的应力水平，往往在横隔板上进行开孔。根据有限元计算结果，横隔板上的应力易在开孔处小圆弧向大圆弧的过渡位置发生应力集中。该位置不与任何其他构件进行焊接，无焊缝存在，选取主应力和vonmises应力进行分析。通过比较，两应力较大值均发生在第二个U 肋穿过的横隔板开孔处外侧，提取该位置在各个工况下的主应力和von-mises应力。横隔板开孔处应力计算位置见图10。

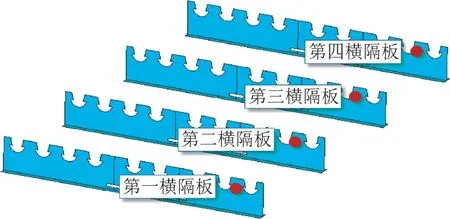
图10 横隔板开孔处应力计算位置Fig.10 Stress calculation position of diaphragm opening

计算结果表明，横隔板开孔小圆弧向大圆弧过渡处的主应力和von-mises应力分布规律相同：

（1）当加载工况位于有横隔板支撑的桥面板上方时（工况1、工况5、工况9、工况13），两种应力最大值均在荷载下方的横隔板处。

（2）当加载点下方无横隔板时，横隔板开孔处的最大应力值出现在与加载位置相临近的横隔板小圆弧向大圆弧开孔处。

（3）在横隔板开孔处，主应力和von-mises应力的最大值都出现在第二个横隔板处，对应于工况5。两应力最大值差别不大，分别为30.60MPa和28.17MPa。

3.3 U肋与横隔板连接位置

在U肋与横隔板连接处的最大应力值主要是由于车轮荷载的面外作用引起。当受到车辆荷载作用时，U 肋由于横向弯曲应力而产生挠曲变形，同时使得横隔板开孔周边产生面外畸变。当横隔板刚度过大且面外畸变受到限制时就会在U肋与横隔板连接处出现相对较大的次内力。横隔板面外畸变和竖向变形是同时进行的，因此纵肋与横隔板连接位置受力很复杂。

通过有限元模型分析可知，在荷载移动过程中U肋与横隔板连接位置的最大应力值出现在横隔板开孔的端部，如图11 所示。在计算过程中发现横向应力均较小，所以只分析竖向和纵向的应力，各个U肋与横隔板连接位置的竖向与纵向应力分布规律如下：

图11 U 肋与横隔板连接处应力计算位置Fig.11 Stress calculation position of the joint between U-rib and diaphragm

（1）当加载工况位于有横隔板支撑的桥面板上方时（工况1、工况5、工况9、工况13），无论是纵向应力还是竖向应力，U 肋与横隔板连接位置的最大应力值都发生在加载点下方的横隔板开孔的端部，当在没有横隔板支撑的地方加载时，该位置的最大应力值出现在加载点临近横隔板的开孔端部。

（2）在单轴荷载作用下，该位置同样也会出现应力集中。

（3）U肋与横隔板连接位置的最大纵向和竖向应力均发生在第二个横隔板开孔端部，最大值分别为10.07MPa和20.57MPa。但应力最大值不是在第二横隔板加载时（工况5）出现的，而是在距第二横隔板左侧0.75m加载时（工况4）出现。

3.4 U肋与桥面板连接位置

经过有限元计算分析，在U肋与桥面板连接位置的应力较大值多出现在沿纵桥向第二个U肋这一条路径上。又因为在不同工况下，此位置所受横向、竖向以及纵向应力都不是很大，所以选取各点在最不利荷载作用下的主应力以及vonmises应力进行分析。应力计算位置见图12，计算结果表明：

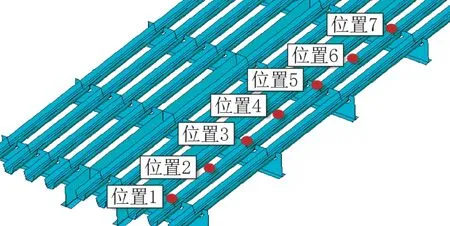
图12 U 肋与桥面板连接处应力计算位置Fig.12 Stress calculation position at the connection between U-rib and bridge deck

（1）无论是主应力还是von-mises应力，最大应力值位于有横隔板支撑的计算位置，即U肋与桥面板以及横隔板三者连接位置，最大主应力为13.85MPa，最大von-mises应力为17.68MPa。

（2）没有横隔板支撑部位的两种应力值都比较小，最大主应力和von-mises 应力分别是1.06MPa、1.39MPa。

（3）和其他计算位置一样，在U 肋和桥面板连接位置也会出现明显的应力集中。

U肋与桥面板连接位置各个计算点在各自最不利受力工况的主应力和von-mises应力见图13。

图13 U 肋与桥面板连接处应力Fig.13 Stress at the joint of U-rib and bridge deck

位于有横隔板支撑的地方的计算点应力值比较大，且高度集中。当加载位置位于第二个横隔板的上方时（工况5），主应力值和von-mises应力值都是最大的。经过以上分析，可以得到对于关注点①、关注点②和关注点④，当加载位置位于第二横隔板上方时（工况5）应力达到最大值。对于关注点③，当加载位置在第二个横隔板的左侧0.75m时（工况4）应力最大。

4 结论

针对某城市轨道交通钢桥同时含有开口T肋与闭口U肋的正交异性钢桥面板，分析了轨道荷载模型在单轴荷载作用下正交异性钢桥面板的整体应力分布状况，确定了关注点的最不利受力工况，并分析同时含有开口T肋与闭口U肋的正交异性板的各个关注点在最不利工况下的应力分布特点，得到如下结论：

（1）对于简化模型在单轴荷载或者双轴荷载作用时，桥面板的整体受力最大值发生在桥面板、U肋与横隔板三者连接位置。

（2）在单轴荷载作用下，关注点①、关注点②和关注点④在工况5 作用下受力最不利，关注点③在工况4 作用下受力最不利。

（3）桥面板的应力主要集中在与横隔板连接位置，横隔板应力主要集中在开孔的外缘，U 肋上的应力主要集中在与横隔板或桥面板连接位置。

（4）正交异性钢桥面板在外力作用下会产生应力集中并且主要发生于各个细部的连接位置。