GNSS 快速驯服高稳晶振的设计与实现

鲁 刚，何在民，王璐璐，王 康，邢 燕，武建锋

（1.中国科学院国家授时中心，陕西西安 710600；2.时间频率基准重点实验室，陕西西安 710600；3.中国科学院大学，北京 100049）

GNSS 系统的时频系统采用多台氢钟、铯钟作为联合守时钟组，产生的GNSS 系统时间具有优良的频率准确度、频率稳定度以及频率漂移率特性[1]。利用GNSS 信号对高稳晶振进行驯服[2]，可实现GNSS 系统时间准确度、长期稳定度与高稳晶振短期稳定度的完美结合[3]。文献[4]设计了一种基于GPS 的1 PPS 信号的二级频标驯服系统。文献[5]针对整个驯服系统进行了相应的测试，介绍了测试方法并且对系统的误差进行了分析讨论。文中利用计数器对接收机的1 PPS 信号与晶振分频产生的1 PPS 信号进行比对，对得到的相位差数据进行野值剔除和滤波，并通过晶振的电压-频率特性得到电压控制字，送入到DAC芯片以实时调整晶振的输出频率，整个系统构成反馈回路[6-11]，最终获得高准确度和稳定度的时频信号。

1 GNSS驯服频标原理

GNSS 驯服高稳晶振是利用GNSS 信号对高稳晶振的频率准确度进行校准，使得高稳晶振的频率准确度和长期稳定度性能得到一定的提升。以北斗/GNSS 定时板卡提供的1 PPS 信号作为参考，采用计数器板卡测量参考1 PPS 信号与高稳晶振分频1 PPS信号之间的时差，微处理器通过串口采集计数器板卡测量的时差值，通过粗差剔除、滤波平滑处理后，获得降噪后的有效时差测量值，由时差测量值计算高稳晶振的频率调整量，然后通过电压控制端进行控制[12-13]。高稳晶振分频1 PPS 信号和参考1 PPS 信号的时差满足以下关系：

式中，a是初始时刻高稳晶振分频1 PPS 信号相对参考1 PPS 信号的时差；b为初始时刻高稳晶振的频率相对于参考频率的频差；c是频率漂移率，也称老化率，是由于高稳晶振自身老化、温度等因素引起的；为随机误差，主要由测量和环境等引起。通常情况下，ξ(t) 服从正态分布，可以通过长时间平滑来降低[14-15]。频率的定义式如下：

对式（2）两边同时进行微分：

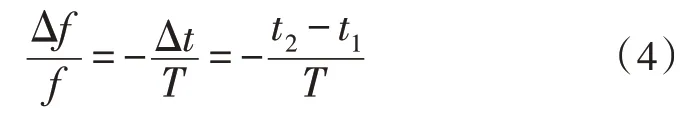
式中右边第二项是误差的次要成分[11]，可以忽略不计。从式（5）中可以看出，频率测量的精度随着比相时间的延长以及对相位差测试精度的提高而提高。

2 驯服系统设计与实现

2.1 硬件设计

根据安全可靠、开发成本低的设计原则，提出了系统的整体设计方案。整个系统由GNSS 定时模块、FPGA、计数器模块、STM32微处理器、高精度DAC1220及高稳晶振组成，其组成框图如图1 所示。

图1 系统总体架构

FPGA 外接晶振输出的10 MHz 频率信号，通过锁相环分频产生1 PPS 信号，和接收机输出的1 PPS信号接入计数器，通过STM32 每秒输入一次查询指令，计数器返回一帧包含相位差的二进制序列，然后STM32 将二进制序列转换成钟差数字量，并进行频差滤波，滤波后的频差值转换成压控晶振的电压控制字，通过SPI 协议送给DAC 模块，对高稳晶振的输出频率进行实时校准，最终把高稳晶振的准确度和稳定度都锁定到GNSS 系统时间。

2.1.1 BDS/GNSS定时板卡

GNSS 定时模块是一款基于ASIC 基带芯片的GNSS 多系统高精度定位板卡。该板卡拥有北斗三频超远距离超快速的高动态解算能力以及超大容量存储功能，并且能稳定输出1PPS 信号。

2.1.2 计数器板卡

计数器板卡的测量功能为测量参考1 PPS 信号上升沿与FPGA 分频1 PPS 信号之间的相位差，通过STM32 向计数器板卡发送开启测量指令帧，每隔一秒发送查询帧，计数器板卡回发一帧数据，经过结算就可以得到相位差数据。

2.1.3 高稳晶振

设计采用的是高稳晶振，属于频率为10 MHz 的高品质产品系列。该系列产品主要有低相噪、高频率稳定度等优点。产品采用密闭的小封装，便于安装集成，其温度稳定度为±5×10-8ppm，线性度为10%。

2.1.4 DAC芯片

DAC1220 分辨率可在满量程范围内达到20 位时，在15 ms 内达到0.003%。输出电压范围2 倍于外部参考电压，同时片上校准电路可动态地减少失调和增益误差[16]。

表1 输出电压选择模式表

对OCXO 的10 MHz±4 Hz 频段的频率控制而言，控制电压变化范围为0～5 V。为了达到设计要求即优于10-11的输出频率精度并留有余量，控制电压的分辨率要达到2×10-5,而DAC1220 转换器在位数为20位的情况下，分辨率如式（6）所示，满足分辨率要求。

1）频率和电压关系

在一定范围内，OCXO 的压控电压与晶振的输出频率成正比关系。DAC1220 电压控制字范围为0x0～0xFFFFF，对应输出电压为0～5 V。在STM32处理器中，先将电压控制字的初始值设为0，每经过一秒的延时，将控制字增加1 000，用SR620 测量晶振输出的频率，利用串口调试助手得到控制字和输出的频率值。高稳晶振电压和频率输出关系如图2 所示。

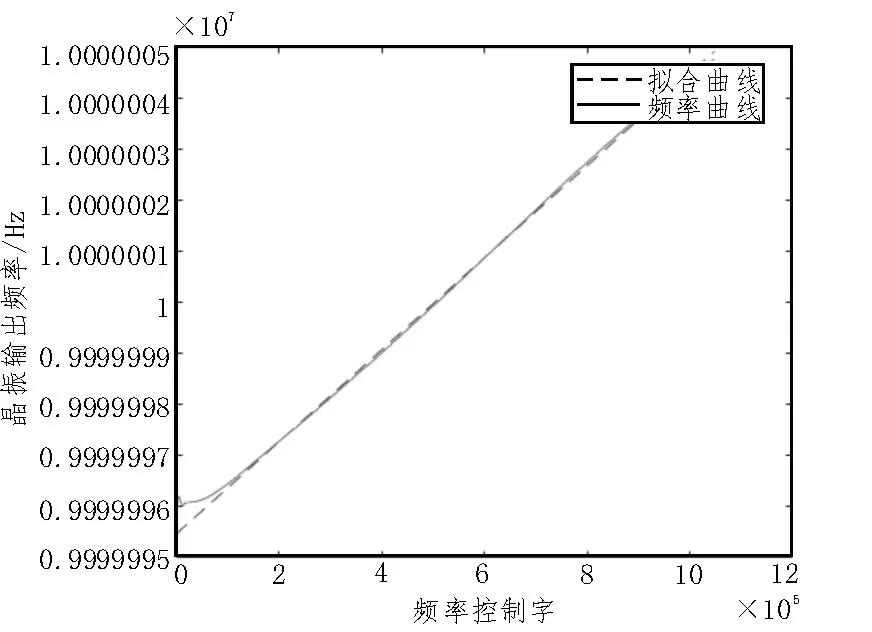
图2 电压控制字与频率关系

实测DAC1220 最大输出电压为4.96 V，从图3 中可以看出，除最初的一段呈现非线性，其余基本近似为一条直线，对频率-电压控制字曲线作线性拟合得到两者关系如下，其线性率为95%，RMSE为0.098 63。

其中，a=0.000 009 24，b=9 999 995.379 47 Hz。

2）控制电压产生

上电根据OCXO 电压和频率输出特性给晶振一个压控电压初始值（511000），使其输出频率为中心频率10 MHz，根据式（7）计算出频率偏差，将频偏值补偿给恒温晶振，通过式（8）改变压控电压控制字：

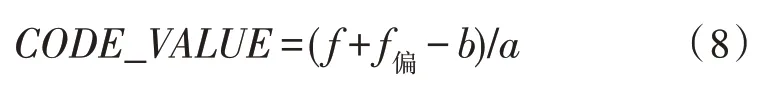
式中，f为上一时刻晶振输出频率值。

2.2 软件设计

系统软件设计流程图如图3 所示。上电系统初始化后，等待晶振预热和K708 板卡稳定输出1 PPS信号，先给一个频率控制字，让晶振输出中心频率，串口中断接收钟差数据，并对相位差数据进行实时处理，利用前100 个数据产生状态估计初始值和初始误差协方差，为剔除异常情况下产生的野值和减小测量噪声，利用Kalman 滤波器对数据进行滤波。在计算出相对频偏值后，实时对晶振的输出频率进行调整。

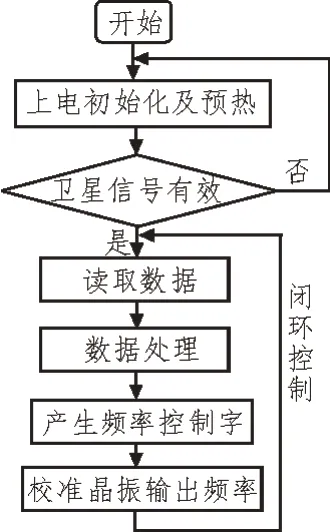
图3 系统主控流程图

2.3 Kalman滤波

定时板卡输出的钟差信号中包含多种误差信号，这些误差大部分都属于随机误差，如果不考虑这些误差，就会对晶振输出频率的稳定性产生很大的影响。为了减小误差给系统带来的影响，必须对相位差的测量结果进行处理，而Kalman 滤波适合解决最佳现象过滤和估计的问题，通过状态方程和递推方法进行处理。它以最小均方误差为准则，用前一个估计值和最近一个观测数据来估算，适用于进行实时处理。因此，该系统采用Kalman 滤波算法对测量结果进行滤波处理，消除干扰。

状态方程如下：

观测方程如下：

协方差计算如下：

最优化估算如下：

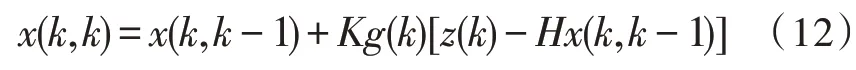
卡尔曼增益计算如下：

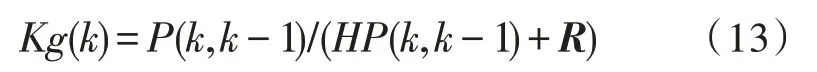
协方差更新计算如下：

式中，x(k)、x(k-1)分别为k时刻和k-1 时刻的系统状态；A是系统参数，z(k)是k时刻的测量值，H是测量系统的参数。随机信号ω(k)和v(k)分别表示过程噪声和观测噪声。P为估计误差协方差，Q为过程噪声的协方差矩阵，R为观测噪声协方差矩阵，Kg为卡尔曼增益。

使用前100 个观测值数据的平均值作为初始状态估计向量，其估计误差协方差初值为：

状态模型的时间常数A取值为1，观测模型的观测参数取值为1。经过多组实验对比，Q、R分别取0.001 和1 时滤波效果较好。

3 驯服系统实验验证与分析

图4 为采集的未经过野值剔除和滤波的相差(时间间隔差)曲线。

接收到的数据会受到各种随机噪声的干扰，导致数据出现较大的跳变，称之为“野值”。从图4 中可以看出，有些点不在正常值范围内。如果不消除这些数据，会对滤波系统产生非常不好的影响，使滤波系统的估计值产生很大的偏差，甚至滤波系统无法收敛，影响系统锁定的精度。程序中可采用3σ准则判断是否存在奇异值，设置此时相应的Kalman 增益为0。经过滤波和奇异值剔除后的相位差数据如图5 所示。

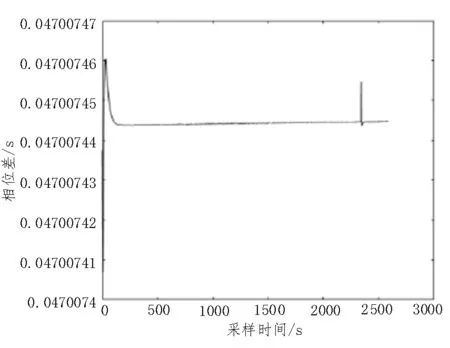
图4 未经滤波的相位差数据

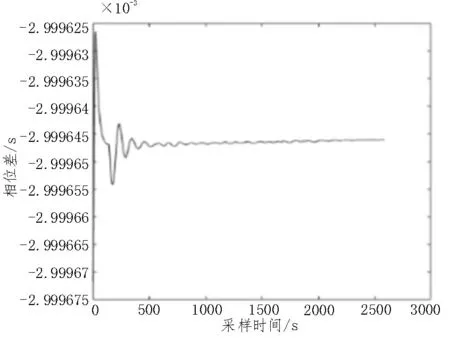
图5 滤波后的相位差数据

从图5 中可以看出，经过约600 s 的振荡，相对频率偏差数据开始收敛，说明频率调整效果明显。

图6 是采集的86 400 s 的数据。经计算，相对频率偏差均值为4.6×10-13，标准差为1.8×10-11。由图6(b)可知，相对频偏数据呈正态分布。

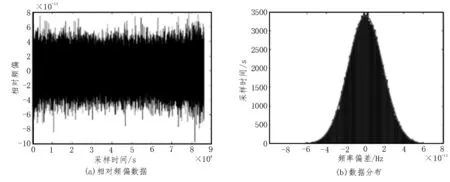
图6 相对频偏数据及其分布

4 结论

文中采用GNSS 信号对准确度为5×10-8的高稳晶振进行驯服，经过约600 s快速调整，晶振频率准确度由10-8提升到10-13量级，实现了GNSS 系统时间准确度、长期稳定度与高稳晶振短期稳定度的结合。