基于矩阵半张量积求解四元数Toeplitz线性系统

李 莹,王玉珊,丁文旭,韦安丽

(聊城大学 数学科学学院，山东 聊城 252059)

近年来, Toeplitz矩阵已经成为科学研究中较为热门的一类特殊矩阵, 它被广泛应用于众多科学领域, 如数字信号处理、数字图像处理、排队网络、数值分析、微分方程数值解等[1]. 在数字信号处理方面, 应用Toeplitz矩阵的特殊结构, 将共轭Toeplitz结构和中央对称Toeplitz结构纳入协方差模型中, 设计了一种基于MOS(model order selection)理论的先分类再检测的检测体系, 来判断接收到的回波信号中是否有目标[2]. 在数字图像处理方面, 将图像退化的过程等价为传输函数和噪声对原始图像矩阵进行线性变换, 而图像恢复过程等价为当传输函数可分离时, 将最小二乘问题转化为Toeplitz矩阵的求逆[3]. 利用系数矩阵Toeplitz的性质打破了在电磁法理论研究中一维理论以及积分方程方法存在的局限性, 使传统积分方程方法中遇到的稠密矩阵的存储困境得到了有效解决. 同时, 利用其所具有的特殊性质, 用快速傅里叶变换实现了迭代算法中的矩阵向量乘积, 加速了传统积分方程技术中直接求矩阵向量乘积的过程[4]. 此外, 针对Toeplitz矩阵特征值的渐近行为, 给出了其在时间序列分析中的应用[5]. 利用上三角Toeplitz矩阵分别给出了常系数线性微分方程和差分方程特解的表达式, 这对求解常系数线性微分方程和差分方程带来了极大的方便[6-7]. 由此可见, 对Toeplitz矩阵的研究具有重要的应用价值.

作为一类特殊的矩阵, 对以Toeplitz矩阵为系数矩阵的线性方程组的求解问题, 以及怎样用计算机来实现算法是主要研究方向之一[8]. 研究方法分为两大类：直接法[9]、迭代法.文献[10]提出了通过分裂Toeplitz矩阵迭代求解线性方程组的HSS方法(skew-Hermitian splitting). 文献[11]提出了将Toeplitz矩阵分裂成一个循环和一个反循环矩阵, 再进行双步迭代求解的CSCS(circulant and skew circulant splitting)方法. 文献[12]提出了将CSCS方法中一个参数形式改进成为两个参数形式的ACSCS(accelerated circulant and skew circulant splitting)方法. Toeplitz系统求解的最新研究进展参见文献[13]. 论文将基于矩阵半张量积,提出一种新的研究四元数上三角Toeplitz线性系统求解的直接方法.

问题1设A∈TQn×n, 令

S={x|x∈n,Ax=b}，

1 预备知识

定义1[14]设M∈m×n,U∈p×q,则

其中：t为n与p的最小公倍数, 当n=p时, 矩阵半张量积转化为普通矩阵乘积.

引理1[14]设x∈m,y∈n, 则

x×y=x⊗y.

注矩阵半张量积是普通矩阵乘积的推广, 具备普通矩阵乘积所具备的性质. 相较于普通矩阵乘积, 学者在矩阵半张量积可交换性方面的研究有着重要的突破.

引理2[14]设x∈t,A为任意矩阵, 则

x×A=(It⊗A)×x.

定义2[14]定义换位矩阵

直接计算即可检验换位矩阵的如下性质

借助于换位矩阵, 可以对矩阵半张量积中的两向量因子的顺序进行交换.

引理3[14]设x∈m,y∈n, 则

W[m,n]×x×y=y×x,(x)T×(y)T×W[m,n]=(y)T×(x)T.

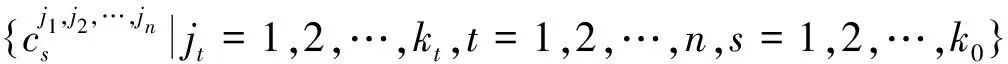
MF称为F的结构矩阵.

引理4[16]设A∈m×n,b∈m,当且仅当AA†b=b时，线性方程组Ax=b有解，且通解表示形式为x=A†b+(In-A†A)y,∀y∈n.

2 四元数矩阵的实向量表示

定义4[17]设q=q1+q2i+q3j+q4k∈, 其中：qi∈(i=1,2,3,4), 并且基底的乘积满足

i2=j2=k2=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j.

定义5设四元数a=a1+a2i+a3j+a4k∈, 称

vE(a)=(a1,a2,a3,a4)T

为四元数a的实向量表示.

根据定义5, 知两个四元数乘积的实向量表示可以转化为两个四元数的实向量表示与四元数乘积的结构矩阵的矩阵半张量积运算, 即引理5.

引理5[18]设l,m∈, 则

vE(lm)=MQ×vE(l)×vE(m),

定义6设xT,y∈n, 称

vE(x)=((vE(x1))T,(vE(x2))T,…,(vE(xn))T)T,

vE(y)=((vE(y1))T,(vE(y2))T,…,(vE(yn))T)T

为四元数向量x，y的实向量表示.

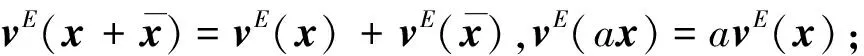
(2) ‖x‖=‖vE(x)‖;

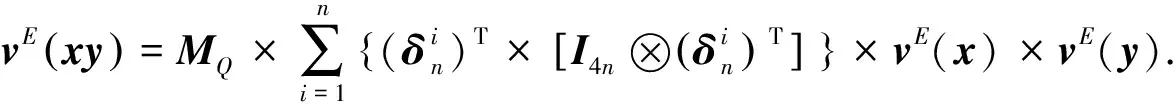
证明(1)，(2)容易验证, 仅对(3)进行证明.

设x=(x1,x2,…,xn),y=(y1,y2,…,yn)T, 则

vE(xy)=vE(x1y1+…+xnyn)=vE(x1y1)+…+vE(xnyn)=

MQ×[vE(x1)×vE(y1)+…+vE(xn)×vE(yn)]=

(3)得证.

借助于四元数向量的实向量表示, 给出四元数矩阵的实向量表示的定义及性质.

定义7设A∈m×n, Colj(A),Rowi(A)分别代表四元数矩阵A的第j列与第i行,j=1,2,…,n,i=1,2,…,m, 分别称

为四元数矩阵A的实列排与实行排.

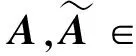
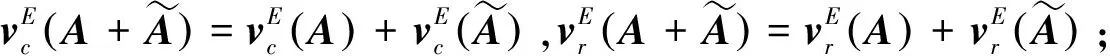
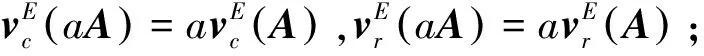
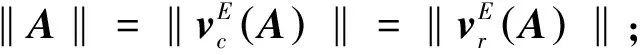
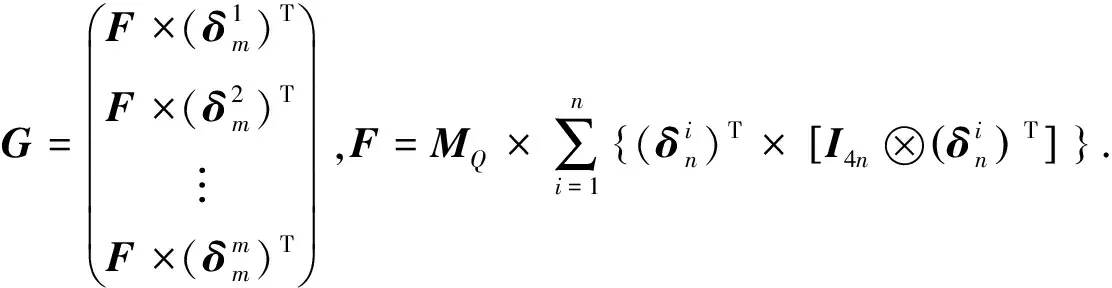
证明(1)～(3)易检验, 仅对(4)进行证明. 首先, 将矩阵A按行分块如下

可以得到Ax=(Row1(A)x,Row2(A)x,…,Rowm(A)x)T, 则

3 问题1的代数解

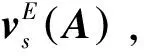
定理3设

则

其中

定理4设A∈TQn×n,x∈n, 则问题1中解的集合S可以表示为

S={x|x∈n,vE(x)=L†vE(b)+(I4n-L†L)y,∀y∈4n},

(1)

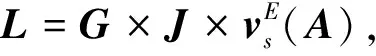
vE(xL)=L†vE(b).

(2)

证明根据定理1，3, 可得

所以,有

‖Ax-b‖=0⟺‖LvE(x)-vE(b)‖=0⟺LvE(x)=vE(b).

对于实矩阵方程LvE(x)=vE(b), 利用引理4, 即得(1)，(2)式.

推论设A∈TQn×n,x∈n, 则四元数上三角Toeplitz线性系统Ax=b有解的充要条件为

(LL†-I4n)vE(b)=0.

(3)

证明利用定理4的证明过程, 可得

‖Ax-b‖=‖LvE(x)-vE(b)‖=

‖LL†LvE(x)-vE(b)‖=‖LL†vE(b)-vE(b)‖=‖(LL†-I4n)vE(b)‖,

则

‖Ax-b‖=0⟺‖(LL†-I4n)vE(b)‖=0⟺(LL†-I4n)vE(b)=0，

从而(3)式得证.

4 算法与数值算例

算法(问题1) 设四元数上三角Toeplitz线性系统Ax=b相容，该算法用于计算极小范数解.

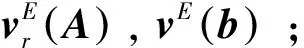
(2) 输入F,G,J, 输出L;

(3) 根据(2)计算Ax=b的极小范数解xL.

算例

在MATLAB中, 借助‘rand’函数随机生成两个向量, 通过‘Toeplitz’ ‘triu’ 函数构造出上三角Toeplitz矩阵Ai与实向量xi(i=1,2,3,4), 借助四元数工具包生成四元数矩阵A∈TQn×n与四元数向量x∈n,计算b=Ax.利用该算法计算得到四元数上三角Toeplitz线性方程Ax=b的极小范数解xL, 将其与真实解x进行比较, 令ε=log10‖xL-x‖, 则ε在不同规模的系统下的值如图1所示.从图1可以看出, 所得到的误差数量级均小于-12, 从而验证了该算法的有效性.

图1 不同规模系统下的误差的数量级