信噪局部方差自适应的小波阈值滤波
万里勇,邓 田
(1.南昌工学院 人工智能学院,江西 南昌 330108;2.江西师范大学 管理科学与工程研究中心,江西 南昌 330022)
高斯噪声常产生于图像的拍摄、传输和处理的过程中,对后续的图像处理与分析产生负面影响,对其有效去除非常必要.高斯噪声服从零均值的高斯分布,相对于其他类型的噪声,高斯噪声的去除往往难度较大,噪声去除与纹理细节的保持往往难以同时达到理想的效果.高斯噪声的数学模型为
Y=X+σN,
(1)
其中:X和Y分别为原图像和噪声图像;σ为噪声的标准差,即噪声强度;N为标准高斯分布:N~(0,1).空间域去噪算法,比如均值滤波[1]以及加权均值滤波算法[2],对高斯噪声的去除性能难以达到图像处理时的质量要求.而小波变换因为具有图像的稀疏表示、时频局部化以及多分辨率分析等良好性能,被广泛应用于图像滤波.最初,文献[3]在高斯模型下,应用多维独立正态变量决策理论,提出了基于小波变换的阈值去噪法.小波变换具有很强的去数据相关性,图像的能量集中于少部分幅值较大的小波系数中,而噪声的能量分布于整个小波域,图像的小波系数大于噪声的小波系数.小波阈值滤波需要一个准确区分信噪系数的阈值,以及对信噪系数进行量化处理的阈值函数[4].Donoho[5]提出了硬阈值和软阈值函数以及统一阈值,如式(2)~(4)所示.硬阈值与软阈值函数都将小于阈值的系数归零,不同的是,硬阈值函数保持其余的系数不变,而软阈值函数为了保持系数的连续性,将其余系数的幅值缩减一个阈值λ.
(2)
(3)
(4)
硬阈值函数的不连续性,导致去噪图像出现伪吉布斯现象.软阈值的连续性保证了图像的平滑性,但是图像系数缩减一个阈值,降低了去噪图像与原图像的相似度,破坏了图像的细节.另外,统一阈值具有明显的盲目性,对所有系数按统一的阈值标准进行处理,缺乏自适应性和鲁棒性[6].
1 相关研究工作
针对硬、软阈值函数的缺陷,Gao[7]提出了半软阈值函数,在保持阈值函数连续的同时,量化的小波系数尽量逼近原小波系数,以减少图像信息的损失.李秋妮等[8]提出一种新的小波半软阈值图像去噪方法,在阈值函数中加入局部相关系数,使其在各种小波变换中均能增强子带内小波系数的相关性.吴安全等[9]提出了一种渐进半软阈值函数,不仅弥补了硬阈值函数不连续性的缺陷,同时还克服软阈值函数重构信号后存在恒定偏差的缺陷.Dehda等[10]提出了一种带形状特征参数的阈值函数(image denoising using new wavelet thresholding function,简称NWTF),在克服硬、软阈值函数缺陷的同时,保持两者的优势.董雪等[11]提出一种基于LoG算子改进的自适应阈值小波去噪算法,在软阈值函数的基础上,对图像非边缘部分的阈值函数加入一个阈值修正系数,而对图像边缘部分,将小波系数附近的能量应用到自适应阈值函数中.王培等[12]在阈值函数中引入调节因子,通过因子的调节,以达到小波系数的最优估计.
将小波阈值去噪与其他技术相结合,优势互补,往往会取得更良好的去噪效果.郭中华等[13]在小波变换中结合多尺度边缘检测,充分考虑了在不同尺度上小波分解的特性,提出一种具有自适应阈值的小波图像去噪改进算法(improved alorithm with auto-adaptive threshold for wavelet image denoising,简称IAAT).Pankaj等[14]提出了一种在小波域中应用局部对比度和自适应均值的图像去噪方法,利用局部对比度和邻域均值对阈值进行设计,同时利用小波系数与对应邻域均值之间的插值对软阈值函数进行改进.非局部均值去噪算法通常受到非相似图像块特别是图像边缘的小权值累积的负面影响,因此,Lu等[15]提出了带软阈值的非局部均值图像滤波方法(non-local means image denoising with a soft threshold,简称NLM-ST),用软阈值去除小权值累积的影响,但是其假设噪声强度为已知,缺乏实用性和可行性,因为现实图像中的噪声强度是不可知的.为了在去除高频图像中噪声的同时去除低频图像的噪声,李嘉浪等[16]提出了基于小波阈值的非局部均值去噪方法,在小波阈值去噪的过程中,对重构的低频图像用非局部均值去噪算法进行去噪处理.显然,对低频图像的非局部均值去噪处理会在一定程度上破坏低频图像的结构,使去噪图像产生模糊效果.Fathi等[17]用小波包变换和优化小波基作为图像的表示工具,用基于小波系数及其子带的均值的优化线性插值方法对小波进行量化处理.Zahra等[18]提出了基于三维小波的双边滤波器,三维小波因其良好的小波定义以及有效的噪声系数表示能力而受到青睐.Ozmen等[19]对文献[18]进行了改进,提出了基于体积子频带加权原理的加权三维小波(a new denoising method for fMRI based on weighted three-dimensional wavelet transform,简称w-3D-DWT)去噪算法,子带加权旨在更好地改善图像表示能力以及自适应地去除图像中的噪声.
为了进一步提升高斯噪声去除的鲁棒性和有效性,作者提出了信噪局部方差自适应的小波阈值滤波方法(wavelet threshold filtering based on adaptive local variance of signal and noise,简称WDALV).该方法提出了一种信噪局部方差自适应的阈值,以及一种连续的、可微且高度逼近原小波系数的阈值函数.实验结果证明,该方法在有效去除高斯噪声的同时,对图像的纹理和细节保持得较好.
2 提出的方法
2.1 信噪局部方差自适应的阈值
作为区分信号系数与噪声系数的阈值,决定着图像去噪的效果.根据图像系数与噪声系数的特征,系数小于阈值的为噪声系数,而大于阈值的为图像系数.阈值过大过度扼杀部分小幅值的无噪的小波系数,但阈值过小会导致去噪不彻底.不同的图像,强度不同的噪声,其小波系数的分布和特征都不一样,以致其适用的阈值也不一样.现有文献中所提出的阈值,没有充分利用图像系数与噪声系数的分布与特征,缺乏自适应性和鲁棒性.
高斯噪声的强度越大,即方差越大,其小波系数的幅值就越大.因此,噪声的方差应作为定义阈值的重要参考,正比于阈值.噪声强度大对应大的阈值,反之,对应小的阈值.图像中的高斯噪声虽然是独立同分布,阈值的定义还应当考虑图像系数本身的方差.一味地将阈值正比于噪声方差,容易使得阈值设置得过大,破坏部分小幅值的图像系数.因此,将图像的标准差作为阈值的制约因子.根据以上分析,结合实验研究,论文提出了基于信噪局部方差的自适应阈值
(5)
其中:σn和σx分别为噪声和原图像小波子带的标准差,根据Donoho等[3]提出的鲁棒中值估计方法对其进行估计
(6)
(7)
其中:HH1为含噪图像的第一层小波分解的对角子带系数.式(5)中的C为系数,为确定其最优取值,将C取不同值的阈值λ结合以下所提出的阈值函数,应用于中等噪声强度(σ=30)的数据集BSD68.去噪图像对应的平均PSNR曲线如图1所示.根据平均PSNR曲线,取C=1.53作为最优值.
2.2 可微且逼近原系数的阈值函数
Donoho[5]最初提出了硬、软阈值函数,分别如式(2)和(3)所示,后续很多学者对其进行了改进.对阈值函数改进的目标,就是设计一个连续的、光滑的且无限逼近原图像系数的阈值函数,其中函数的光滑性体现于函数的可微性.函数的连续和光滑能够避免去噪图像出现伪吉布斯现象,而函数无限逼近原图像系数能够避免丢失图像的原始信息,保持图像的边缘和细节.提出一个同时具有这3个特性的阈值函数有一定的难度,因为连续、光滑与无限逼近存在着顾此失彼的关系,现有文献中的阈值函数只是作出相应的折中.为了更好地实现小波系数量化去噪处理的连续性、光滑性和逼近性,论文提出一种连续的、可微和无限逼近原图像系数的阈值函数,如式(8)所示,其函数图像如图2所示.
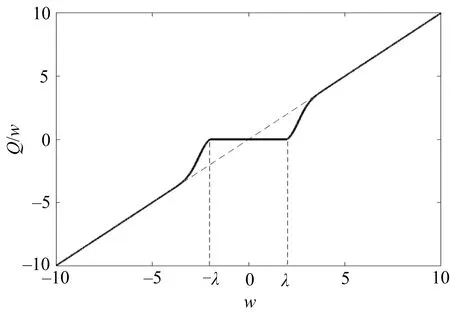
图2 论文提出的阈值函数
(8)
其中:r=1-e-(|w|-λ)2.
根据图2可以直观地看出,所提出的阈值函数具有连续性、良好的光滑性以及无限逼近性等数学特性.以下根据函数表达式证明Q(w)的连续性、可微性和逼近性.因为Q(w)满足Q(-w)=-Q(w),为奇函数,只需证明Q(w)的单边数学特性即可.
(1) 函数的连续性.因为
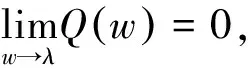
(2) 函数的可微性.由
可知Q(w)在λ处的左导数等于右导数,所以在λ处可导.又在区间(λ, +∞),有
所以,Q(w)在区间(λ, +∞)可导.对于区间[-λ,λ],Q(w)为常数,可导,因此Q(w)在整个定义域上可导.
(3) 函数的逼近性.由
可以看出Q(w)以Q(w)=w为渐近线.同时,有
所以,在|w|>λ时,λ(x)无限拟合原小波系数.
根据以上分析,所提出的Q(w)函数具有连续性、可微性和高度逼近性,具有良好的数学特性,所以能根据阈值λ更有效地对含噪的小波系数进行量化处理.
3 实 验
以数据集BSD68中的部分图像以及部分医学图像作为实验图像,如图3所示.在Intel(R) Core(TM) i5-4590 CPU @ 3.30GHZ, 8GB RAM 的计算机上用MATLAB R2013b 进行实验.根据去噪结果的峰值信噪比(PSNR)和结构相似性指数(SSIM),将所提出的WDALV算法与现有文献中最新提出的且有代表性的部分算法作比较,以验证WDALV算法的有效性和鲁棒性,这些算法分别是NWTF[10],IAAT[13],NLM-ST[15],w-3D-DWT[19].

图3 实验图像
3.1 去噪处理的PSNR和SSIM
各算法对含各种强度高斯噪声的图像test013和chest_xray进行去噪处理得到PSNR和SSIM值分别如表1和2所示.
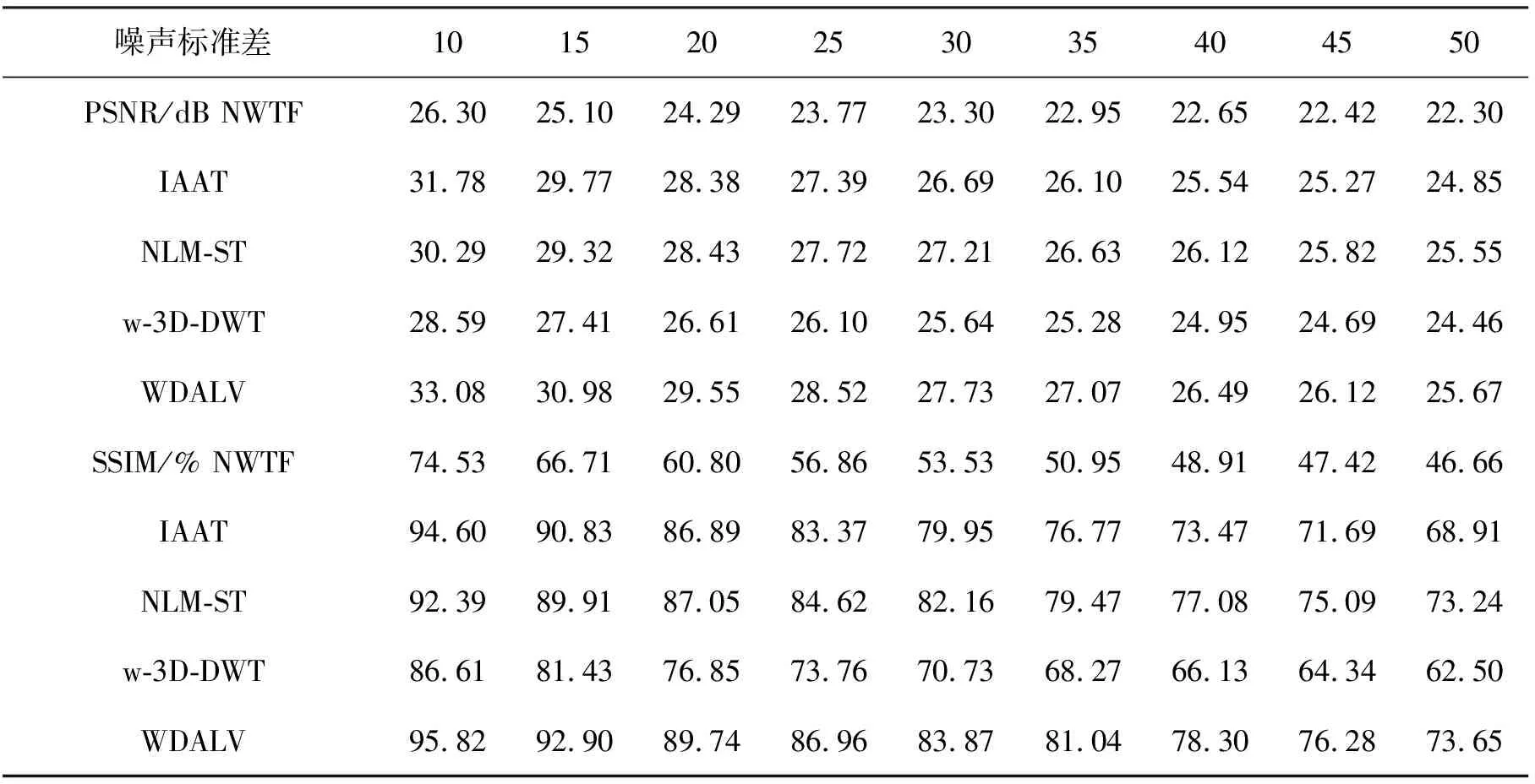
表1 各算法对的test013去噪处理的PSNR和SSIM值
从表1中的数据大小、其随噪声强度的走向以及各算法数据之间的差距可以看出,所提出的算法中WDALV的PSNR和SSIM值均大于其他算法,在噪声强度较小时相对于其他算法的优势异常显著,这表明WDALV在保持去噪图像与原图像较高相似性的同时,较好地保持和恢复图像的细节和纹理结构.各算法中效果最差的是NWTF,其PSNR和SSIM均最小,原因在于其所提出的带形状特征参数的阈值函数的最优参数不具有鲁棒性,对不同的图像适用的最优参数差别较大.w-3D-DWT在噪声强度较小时,其去除效果较差,而在噪声强度较高时,去噪效果可以接受.相对地,IAAT和NLM-ST取得了良好的去噪效果,两者在去噪和纹理结构的保持上的性能相当,虽然在同等噪声强度下其PSNR和SSIM值接近WDALV,但是WDALV的PSNR和SSIM依然比它们分别大致高出0.8 dB和1.7%.
表2显示了各算法对医学图像chest_xray的去噪结果.从表中的数据可知:①NWTF的去噪性能始终是最差的,其PSNR和SSIM值最小,与其他算法有明显的差距.②NLM-ST与w-3D-DWT的去噪性能差别不大,均处于中等水平;相对地,IAAT的去噪性能较好,特别对于低强度的噪声,其优越性更加明显.③在去噪性能和纹理结构的保持和恢复上,WDALV算法相对于现有算法的优越性明显,通过较大的PSNR和SSIM体现出来;对于每种强度的噪声,WDALV都取得最大的PSNR和SSIM值,比性能较好的IAAT分别大致高出0.7 dB和2.3%.

表2 各算法对chest_xray去噪处理的PSNR和SSIM值
3.2 去噪处理的视觉效果
为了在视觉感知上验证去噪结果的性能,以含噪强度σ=20的test049和σ=30的医学图像breast_xray作为实验图像.各算法对应的去噪图像分别如图4,5所示.分图题中的两个数字分别是分图对应的PSNR和SSIM值.
图4中,从视觉感知上,NWTF的模糊效果比较严重,原图像的细节和纹理结构已经丢失,只能看见图像的大致轮廓.同样地,w-3D-DWT的模糊效果比较明显,未能恢复图像的细节.IAAT和NLM-ST的去噪效果相对良好,IAAT对纹理结构保持得很好,但是依然存在少量可见的噪声,去噪不彻底,而NLM-ST去噪比较彻底,但是依然出现轻微的模糊效果.相对地,WDALV的去噪效果最好,将其去噪图像和原图进行比较,可见其在彻底去除噪声的同时,大部分的细节和纹理结构都恢复得很好.相对于性能较好的算法IAAT和NLM-ST,WDALV在细节和纹理结构的保持方面其优势还是明显的.进一步地,根据各去噪图像对应的PSNR和SSIM值所得出的结论,与视觉感知基本上是一致的.

图4 各算法对含噪强度为σ=20的test049的去噪图像
图5 中,对含噪强度为σ=30的医学图像breast_xray,NWTF和NLM-ST的去噪效果较差,去噪图像出现明显的模糊效果,大部分的图像脉络已经丢失.w-3D-DWT的效果图从视觉上可以接受,但是其模糊效果依然比较明显.相对地,IAAT取得了较好的去噪效果,图像的脉络清晰.同样地,WDALV的去噪图像较清晰,细节和脉络保持得很好,与IAAT相比,从视觉上难以分辨孰优孰劣,但从量化的数据PSNR和SSIM可以看出,相对于IAAT,WDALV在效果图与原图的相似性及结构纹理的恢复上还是占有一定的优势.
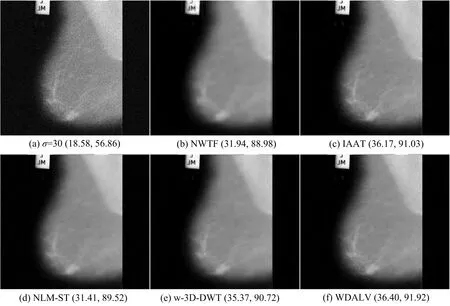
图5 各算法对含噪强度为σ=30的breast_xray的去噪图像
4 结束语
为进一步提升高斯噪声的去除效果,提出了一种信噪局部方差自适应的小波阈值滤波方法.其用信噪局部方差自适应的阈值对图像的信号系数与噪声系数进行区分,然后用连续的、可微且无限逼近原图像系数的阈值函数对小波子带系数进行量化处理.实验结果表明,论文方法相对于现有的方法具有更好的去噪性能,对于各种强度的高斯噪声及各种图像,其都能取得良好的去噪和边缘细节保持的效果.

