基于CPSO-PNN及灰色关联度分析的电网分区故障诊断

谢 民，邵庆祝，王同文，俞 斌，张 倩

(1.国网安徽省电力有限公司 电力调度控制中心,安徽 合肥 230022；2.安徽大学 电气工程与自动化学院，安徽 合肥 230601)

电网规模扩大和新能源接入，使电力系统结构越来越复杂，给电网故障诊断带来难度.电网故障诊断的主要方法有：专家系统[1]、贝叶斯网络[2]、粗糙集理论[3]、模糊理论[4]、人工神经网络[5]、遗传算法[6]、Petri网[7-8]、解析优化[9]等.专家系统有知识库建立和维护难、推理速度慢等不足之处.贝叶斯网络的系统参数若不能合理设置，则大幅降低故障诊断精度.使用粗糙集理论诊断故障时，决策表建立难度大，重要信息丢失会降低诊断准确率.模糊理论构建与电网拓扑结构相适应的隶属度函数模型难度较大.在拓扑结构复杂、节点数多的情况下，Petri网的关联矩阵维数大，因而计算量大.解析优化有严密的理论结构，但建立目标函数难度大.人工神经网络具有学习能力强、易实现、鲁棒性强、处理噪声响应快等优点，故广泛应用于故障诊断领域.

人工神经网络的分区电网故障诊断，将大电网分成多个区域，再对区域进行故障诊断[10]，减小了大型电网故障诊断建模的难度.文献[11]提出了电网分区的策略，但没有解决重合区域故障诊断的问题.文献[12]采用非重合分区法对电网进行分区，然后进行故障诊断，该方法虽然可以避免重合区域的重复诊断，但不能保证分区后各区域子网具有连续性.

该文拟提出基于混沌粒子群优化的概率神经网络及灰色关联度分析的电网分区故障诊断方法.将整个电网结构划分为若干区域，对不同区域构建相应的故障诊断模块，利用概率神经网络(probabilistic neural network，简称PNN)诊断故障.平滑因子作为影响概率神经网络训练的重要参数，直接影响故障的诊断精度，因此采用混沌粒子群优化(chaos particle swarm optimization，简称CPSO)算法[13]确定平滑因子的最优解.概率神经网络的电网分区故障诊断中，重合区域的故障会同时触发两个或两个以上区域的神经网络诊断模块，输出结果并不唯一.针对该问题，利用灰色关联度分析(gray relational analysis，简称GRA)[14-15]，对重合区域的多组神经网络输出结果进行故障再分析，以提高重合区域故障的诊断精确.通过仿真分析验证该文方法的有效性.

1 混沌粒子群优化的概率神经网络

1.1 概率神经网络

PNN是一种径向基函数前馈神经网络[16].PNN采用径向基函数，具有较强的容错能力，只要样本数据足够，就不会陷入局部极小，其结构如图1所示.

图1 PNN的结构

模式层的输出为

(1)

其中：φij表示输入向量与中心的距离；X=(x1,x2,…,xn)为输入样本；xij为第i个训练样本的第j个中心，i=1,2,…，n，j=1,2,…,n；d为特征向量的维数；σ为平滑因子.

求和层的输出为

(2)

其中：vi表示模式层输出的加权平均；L为第i类神经元的数量.

输出层的输出为

yi=arg(max(vi))，

(3)

其中：yi为元件的故障度.

1.2 混沌粒子群优化

CPSO算法是基于PSO(particle swarm optimization)的混沌优化算法.在n维搜索空间中，第k次迭代后第i个粒子的位置、速度分别为Xi(k)={xi1(k),xi2(k),…,xin(k)}，Vi(k)={vi1(k),vi2(k),…,vin(k)}.第(k+1)次迭代后第i个粒子的位置、速度分别为

Xi(k+1)=Xi(k)+Vi(k+1)，

(4)

Vi(k+1)=ω(k)Vi(k)+c1r1(lbesti(k)-Xi(k))+c2r2(gbesti(k)-Xi(k))，

(5)

其中：ω(k) 为第k次迭代的惯性权重；c1为搜索空间的认知参数，c2为搜索空间的社会参数；lbesti(k)为第k次迭代后第i个粒子的局部最佳位置，gbesti(k)为第k次迭代后第i个粒子的全局最佳位置；r1，r2为位于[0 ，1]的随机数.

第(k+1)次迭代后的参数为

ω(k+1)=4[ωmin+(ωmax-ωmin)ω(k)][1-ωmin+(ωmax-ωmin)ω(k)]，

(6)

cz(k+1)=4[cmin+(cmax-cmin)cz(k)][1-cmin+(cmax-cmin)cz(k)]，

(7)

rz(k+1)=4r(k)[1-r(k)]，

(8)

其中：ωmax，ωmin分别表示最大、最小惯性权重；cmax，cmin分别表示最大、最小搜索空间参数；z=1,2.

1.3 CPSO-PNN

PNN的平滑因子σ直接影响PNN的训练精度和收敛速度，进而影响故障诊断的精度及速度.因此，该文将CPSO与PNN相结合(CPSO-PNN)确定σ最优解，以提高PNN的性能.CPSO的适应度为

(9)

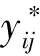
图2为CPSO-PNN的流程图.具体步骤如下：

图2 CPSO-PNN的流程图

(1) PNN和CPSO初始化.将PNN的平滑因子视为粒子，构建粒子群.对CPSO的每个粒子的位置和速度进行初始化.设置最大迭代次数.

(2) 计算每个粒子的MSE，确定粒子的lbest和gbest.

(3) 判断是否满足终止条件，若否，则进入步骤(4).

(4) 根据式(4)～(8)更新粒子的位置和速度.

(5) 重复步骤(2)～(4)，直至满足终止条件.

2 电网故障诊断方法

2.1 重合区域的故障诊断

重合区域的故障会触发两个或者两个以上区域的神经网络进行故障诊断，即会得到两个或者两个以上的诊断结果，因此须对神经网络的输出结果进行灰色关联度分析，以得到更精确的结果.

设区域总数为j.将区域i(i=1,2,…,j)神经网络期望输出记为参考序列Xi，其表达式为

Xi={x0(1),x0(2),…,x0(k)}，

其中：k为区域i的元件数.

将区域i神经网络诊断输出记为比较序列X′i，其表达式为

其中：m为区域i的故障数.

对神经网络的输出进行灰色关联度分析的具体步骤如下：

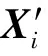
(10)

其中：i=1,2,…,j；q=1,2,…,k；ρ(ρ∈(0,1))为灰色关联度的分辨系数，一般取0.5[14].

(2) 计算Xi和X′i间的灰色关联度

(11)

(3) 计算综合灰色关联度

(12)

(4) 对T进行归一化后，计算元件的故障度

(13)

(5) 判断故障元件.若H大于0.5，则该元件为故障元件，否则为正常元件.

2.2 故障诊断流程

图3为故障诊断流程.具体步骤为：

(1) 将电网整体结构划分为n个区域.

(2) 提取区域i的告警信息作为训练样本，训练区域i的神经网络.

(3) 建立区域对应的CPSO-PNN故障诊断模块.

(4) 对故障告警信息进行预处理，发生故障的区域触发对应的神经网络诊断模块.

(5) 判断是否为重合区域故障.若否，则对故障结果进行诊断分析；若是，则对故障进行灰色关联度分析.

(6) 分析诊断结果，得到故障点.

将该文提出的故障诊断方法简称为CPSO-PNN-GRA.

3 仿真分析

3.1 电网分区

该文选择IEEE 14节点电力系统为仿真模型，如图4所示.图4中，蓝色背景部分为重合区域，根据蝶形分区法[17]将系统划分为4个区域.

图4 IEEE 14节点电力系统

3.2 故障诊断

提取各区域一定数量的典型故障构成训练样本集，对各区域进行训练.故障样本的神经网络输入采用二进制形式，即1表示保护装置动作或者断路器跳闸，0表示保护装置未动作或者断路器未跳闸.如果神经网络输出结果大于0.5，则认为对应的元件为故障元件.

图5为4个区域4种算法的适应度，其中的4种算法为差分 (differential evolution，简称DE)、PSO、CPSO、遗传算法(genetic algorithm,简称GA).由图5可看出，相对于DE,GA及PSO，CPSO的收敛速度最快，且没有陷入局部最优，表明其有很好的全局搜索能力.

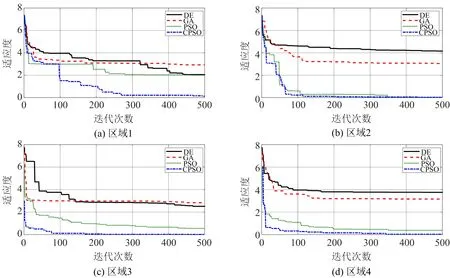
图5 4个区域4种算法的适应度

表1为区域1两种算法的训练结果.由表1可知， CPSO的成功率达99%，比PSO的成功率高；CPSO的训练时间为237 ms，比PSO的训练时间少.

表1 区域1两种算法的训练结果

对训练好的神经网络，选择若干重合区域和非重合区域故障进行诊断，验证该文所提方法的有效性.选取400个训练样本训练神经网络，选取60个诊断样本进行故障诊断.几种典型诊断样本的相关情况如表2所示.

表2 几种典型诊断样本的相关情况

表3为非重合区域故障元件的CPSO-PNN故障度.由表2～3知，CPSO-PNN能准确诊断出非重合区域故障元件.

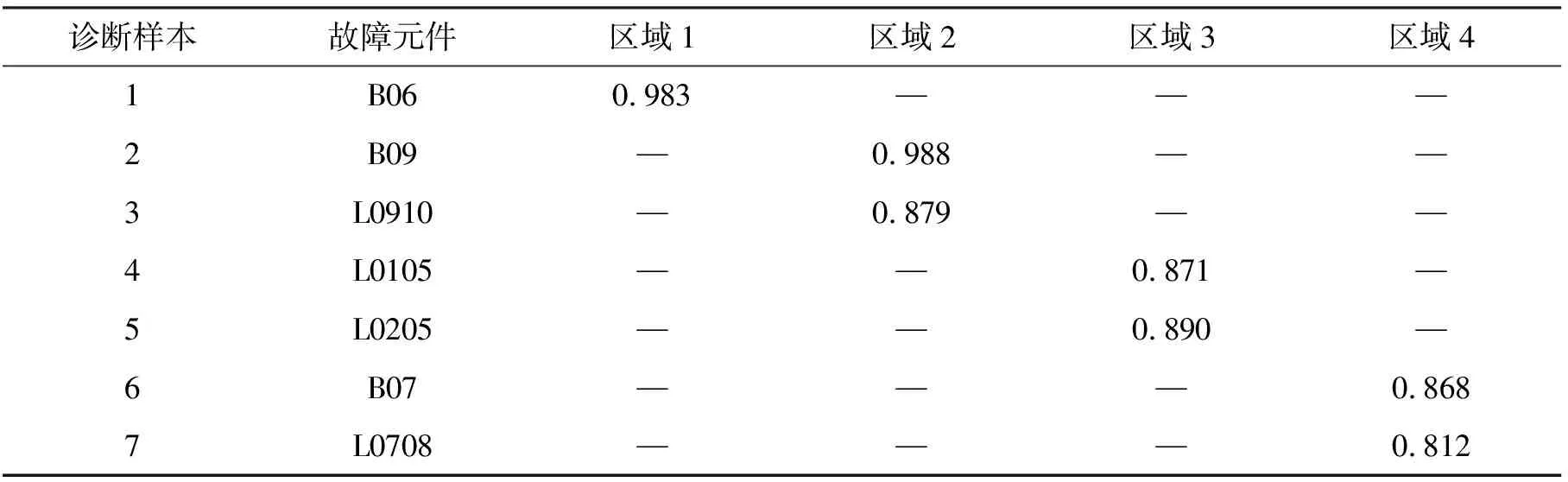
表3 非重合区域故障元件的CPSO-PNN故障度

注：“—”表示无法获得.

表4为重合区域CPSO-PNN-GRA及模糊积分[10]的故障诊断结果.由表4可知， CPSO-PNN-GRA能诊断出全部故障元件，而模糊积分未诊断出全部故障元件，因此CPSO-PNN-GRA方法优于模糊积分方法.

表4 重合区域2种方法的故障诊断结果

表5～8分别为使用CPSO-PNN-GRA方法得到的区域1～4的诊断结果.

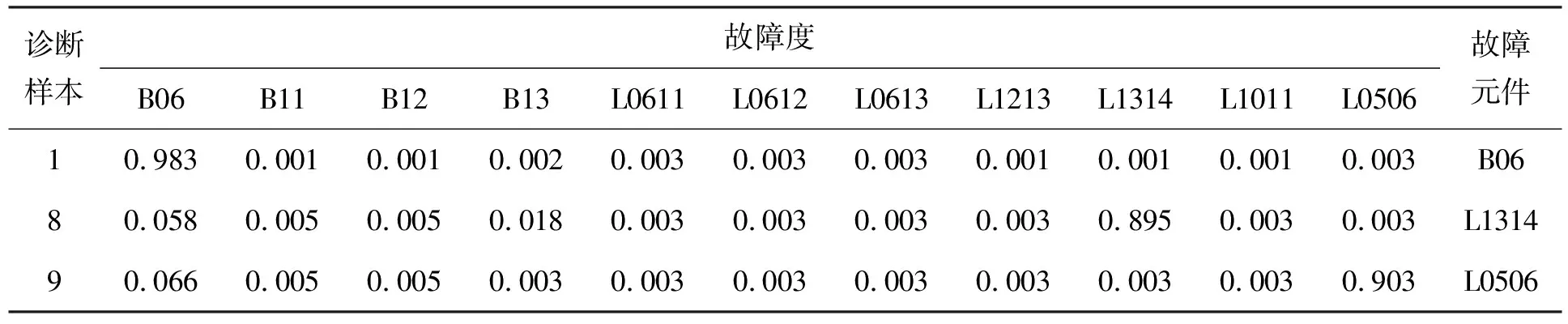
表5 区域1的诊断结果

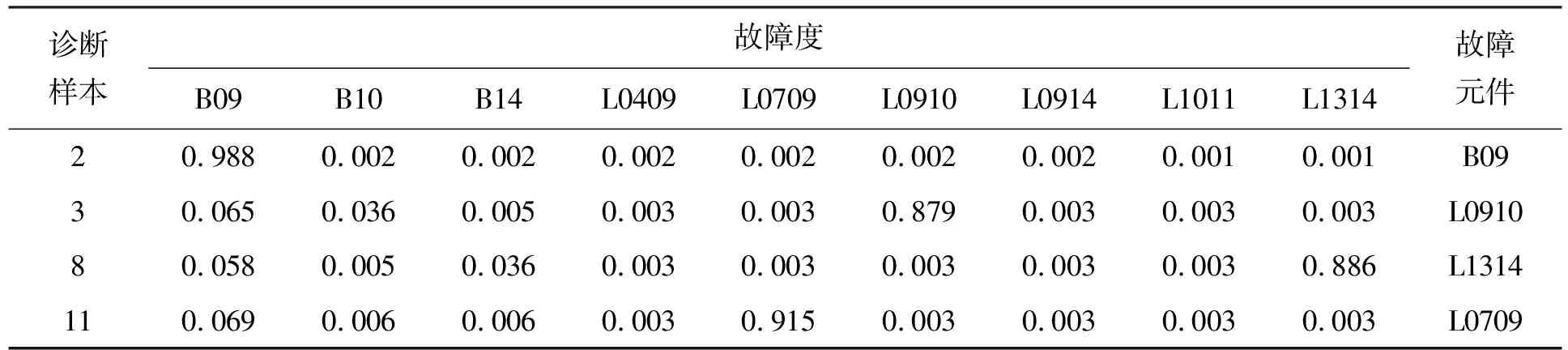
表6 区域2的诊断结果

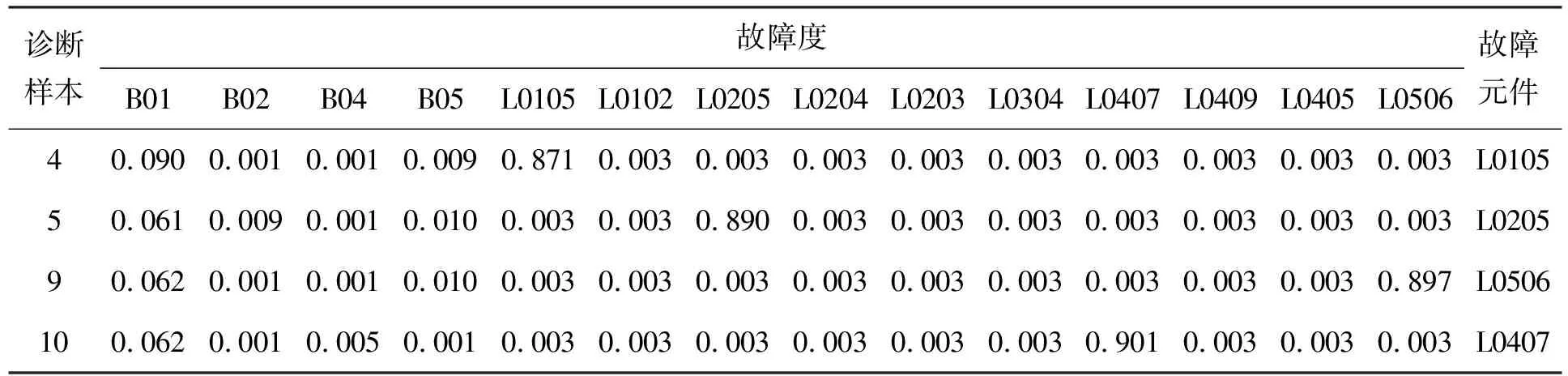
表7 区域3的诊断结果

表8 区域4的诊断结果

4 结束语

该文提出基于CPSO-PNN及灰色关联度分析的电网分区故障诊断方法，对复杂的大电网结构采取先分区后诊断的策略，降低了诊断难度.在PNN训练过程中，利用CPSO对PNN进行改进，提高了网络的性能.在故障诊断过程中，对重合区域利用GRA对重合区域的概率神经网络诊断模块的输出结果进行二次分析，实现了重合区域的故障诊断.仿真结果表明：该文提出的分区故障诊断方法不仅能诊断单个故障，而且能诊断多个故障和重合区域故障，具有较高的故障诊断精度.当电网分区或者电网结构发生变化时，必须改变神经网络结构，调整神经网络参数，使其适应变化的电网分区.因此，电网分区变化对故障诊断模型的影响，将是下一步的研究内容.