基于混合特征选择的脑电解码方法
莫 云
(桂林航天工业学院电子信息与自动化学院,广西 桂林 541004)
0 引 言
在运动想象脑电解码中,特征选择非常重要。由于运动想象脑电存在个体差异,因此需要特征选择方法选择被试特异的频带特征、时间窗特征、通道特征等[1]。另外,融合特征也需要特征选择方法选择更具判别性的特征。单一特征或者少数特征不需要特征选择,但是单一特征通常不能更好地表征完整的脑电信息。融合特征有利于实现信息互补[2],但是通常也包含噪声和冗余信息。因此,融合特征需要特征选择剔除无效信息。此外,特征选择可以降低特征维数,减少分类模型的复杂度,避免维数灾难和过拟合。
现有特征选择方法主要包括过滤式(Filter)、包裹式(Wrapper)和嵌入式(Embedded)3类[3]。过滤式特征选择方法使用信息度量和距离度量等评价准则选择特征,比如Fisher分数[4]、互信息[5]、散度[6]等。包裹式特征选择方法使用特定的方式产生特征子集,然后使用分类器的结果作为特征选择的评价标准。包裹式方法大多基于智能优化算法,包括粒子群优化(Particle Swarm Optimization, PSO)算法[7]、遗传算法(Genetic Algorithm, GA)[8]、人工蜂群算法[9]、萤火虫算法[10]等。嵌入式特征选择方法在分类器训练的时候自动把一些特征剔除,因此可以同时进行特征选择和分类。比较典型的嵌入式特征选择方法有最小绝对值收缩和选择算子(Least Absolute Shrinkage and Selection Operator, LASSO)方法[11]。LASSO在线性回归模型中加入l1-范数正则化惩罚项,使得部分特征的权重系数近乎归0,特征选择通过剔除系数为0或者接近0的特征实现。Miao等[1]使用LASSO对运动想象时-频-空域的特征进行选择。王金甲等[12]使用稀疏组LASSO同时进行运动想象信号的通道选择和特征选择。
以上3类方法都各有优缺点,各类方法之间的有机结合可以实现优势互补。因此,混合特征选择方法近年来也得到了比较广泛的研究。裴作飞等[13]使用卡方过滤算法剔除冗余特征,然后再使用LightGBM和自适应遗传算法组成的封装方法进一步约减特征。江泽涛等[14]使用Fisher分数(Fisher Score, F-score)对特征进行降维处理,然后引入超图的Helly属性对得到的特征子集进行二次筛选。肖艳等[15]提出了基于Relief F和PSO的混合特征选择方法,先使用Relief F滤除相关性小的特征,然后以PSO作为搜索算法,并使用支持向量机作为评估函数,进一步选择出最优特征子集。Ghareb等[16]结合6种过滤式特征选择方法和改进的遗传算法组成新的混合特征选择方法。文献[17]是一篇综述性文章,全面介绍了用于癌症分类(基于微阵列基因表达数据)的混合特征选择方法。Eslahi等[8]使用遗传算法寻找特征提取方法和分类器的最优组合。Qi等[18]提出了多级混合PSO-贝叶斯线性判别分析方法,用于运动想象的通道选择和特征选择。虽然混合特征选择方法已经得到了较为广泛的应用,但据了解,除了文献[8]和文献[18],很少见到有相关文献研究报道混合特征选择方法在脑电特征选择中的应用。
以上的混合特征选择方法大多基于遗传算法和PSO等智能优化算法,模型训练时间长,而且容易陷入局部最优解。为了同时兼顾特征选择的时间效率和分类性能这2个问题,本文提出2种混合特征选择方法,分别是基于LASSO的混合特征选择方法以及基于Fisher分数的混合特征选择方法。首先分别使用LASSO模型和Fisher分数获取特征的权重。然后设置一系列的阈值,大于设定阈值的特征将被选择。最后结合Fisher线性判别分析(Fisher Linear Discriminant Analysis, FLDA)和交叉验证选择最优的阈值参数,继而得到最优的特征子集。使用3个数据集验证混合特征选择方法的有效性。实验结果表明,2种新提出的方法不仅分类结果较好,而且特征选择时间也具有显著优势。
1 方 法
1.1 算法框架
图1给出了本文方法的算法框架。首先,对输入的原始脑电信号进行预处理,包括8~30 Hz带通滤波和0.5 s~2.5 s时间窗截取。其次,对预处理的数据进行CSP变换。针对CSP空间滤波后的信号,提取对数方差、4阶自回归(AutoRegressive, AR)系数、带通功率和小波能量4种特征,并进行特征融合。接着,使用特征选择方法对融合特征进行选择。最后,使用FLDA分类器对各种方法选择的特征子集进行分类。
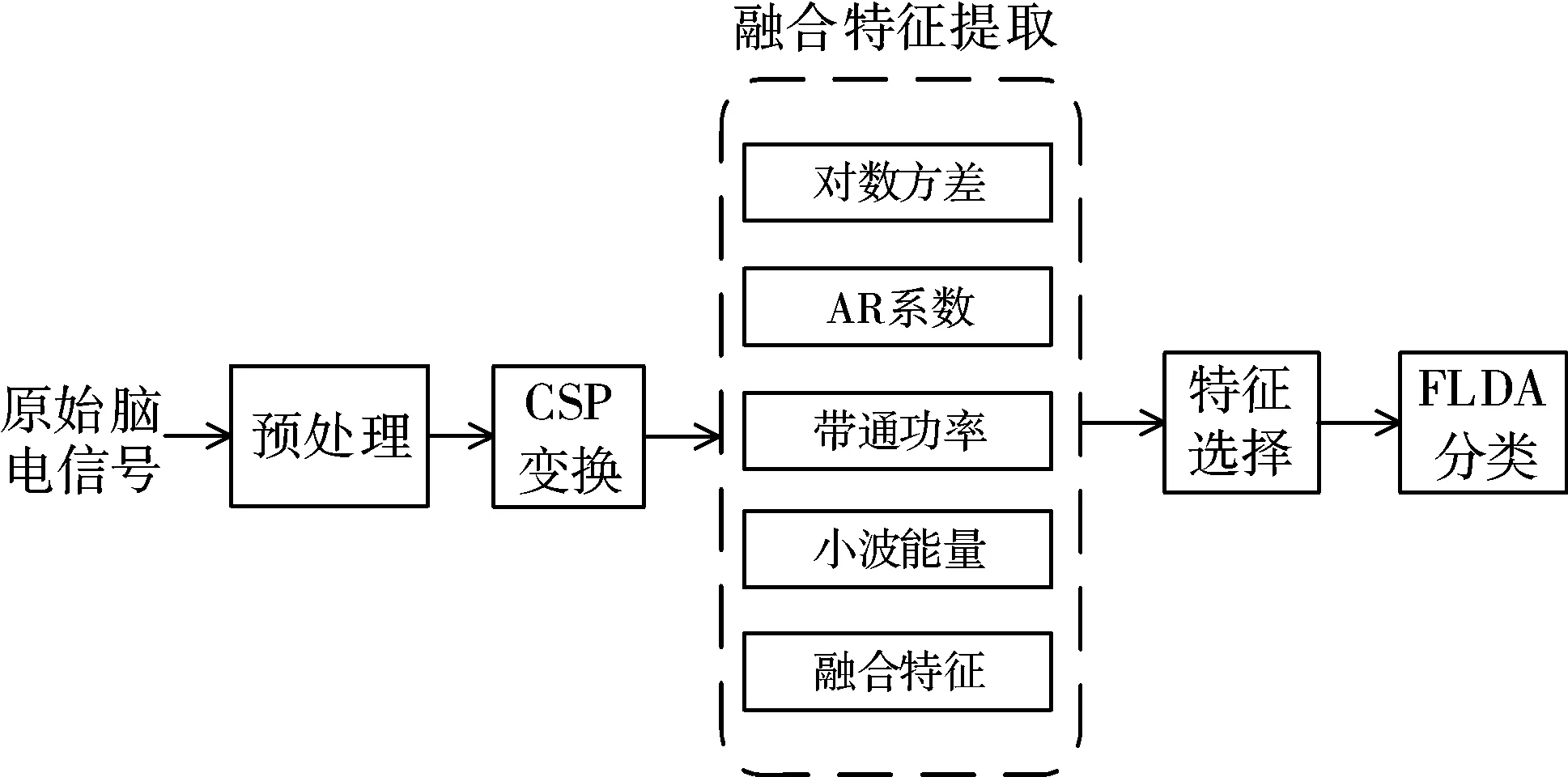
图1 算法框架
1.2 特征提取
传统的时域、频域和时频特征提取方法直接对预处理后的脑电信号提取相应的特征,本文的特征提取与传统方法有所不同。受文献[3]启发,在特征提取过程中,先进行CSP变换,然后再提取对数方差、4阶AR系数、带通功率和小波能量4种特征,并进行特征融合,特征融合过程详见图2。这样做有2个好处:1)信号经过CSP空间滤波之后,信号质量提高,提取的特征更加稳定、更具判别性;2)经过CSP空间投影之后,信号通道减少,特征提取的时间也相应减少。在本文中,对于数据集1和数据集3,CSP的空间滤波器对数选择为3;对于数据集2,滤波器对数选择为1。CSP的实现以及对数方差特征的计算可参考文献[19],AR系数、带通功率和小波能量的特征提取可参考文献[20]。
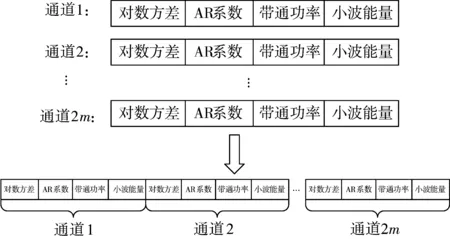
图2 融合特征的计算过程
1.3 特征选择
不同被试在进行运动想象的过程中存在个体差异性,而且不同被试其判别性特征也有所区别,所以使用单一特征不能很好地表征脑电信息。融合特征结合多种类型特征可以实现信息互补,而融合特征的维数过多,又会造成信息冗余,故需要进行特征选择。下面将介绍本文所提出的2种混合特征选择方法。
1.3.1 基于LASSO的混合特征选择方法
LASSO在线性回归模型的基础上,引入l1-范数对模型的权重进行约束,其数学模型如下:
(1)
其中X=(x1,x2,…,xN)T为样本矩阵,X∈N×P,N为样本数,P为样本的特征维数。y=(y1,y2,…,yN)T∈N为样本标签向量,yi∈{-1,1}。w=(w1,w2,…,wP)T∈P为特征权重系数向量,是正则化参数,决定了模型的稀疏度。当λ增大时,‖w‖1变小,导致w的某些元素趋于0,也即特征权重趋于0,被选择的特征减少;当λ减小时,‖w‖1变大,导致w非0的元素增多,被选择的特征增多。因此,LASSO可以用于特征选择。在权衡分类准确率和模型复杂度之间,需要使用训练数据选择一个合适的λ值以及最优的LASSO模型。w的权重系数越大,说明对应的特征对分类越重要。
一般使用交叉验证和网格搜索方法选择最优的LASSO模型参数,然后筛选出特征权重不为0的特征子集进行后续的分类。由于脑电信号的随机性和非平稳性,通过LASSO选择出的权重不为0的特征子集可能还包含有冗余信息。因此,有必要再做一次特征选择。因此,在本文中,设置特征权重的阈值为T∈{0,0.1,0.2,…,0.8},再次使用交叉验证和网格搜索方法选择最优的阈值,特征权重大于设定阈值的特征将被选择。使用FLDA的分类准确率作为评价准则,把最高的交叉验证平均分类准确率所对应的阈值作为最优阈值。这样就通过LASSO和FLDA分类器组成了一种混合的特征选择方法。该方法通过LASSO嵌入式特征选择方法进行特征子集预选,然后再使用包裹式方法进行二次特征筛选。
在本文中,2次交叉验证都选择10折交叉验证。LASSO模型参数λ的备选合集为{0.1,0.2,…,3}。
1.3.2 基于F-score的混合特征选择方法
F-score可以衡量特征在2个类别之间的区分能力。F-score通过计算每个特征的类间和类内的方差比得到,具体如下:
(2)
其中,xk∈P,k=1,2,…,n,xk表示第k个样本,n为样本总数。正类和负类的样本数分别为n+和n-,则n=n++n-。F(i)代表第i个特征的Fisher分数。和分别为第i个特征在整个数据样本集上的平均值、在正类样本集上的平均值和在负类样本集上的平均值。为第k个正类样本点的第i个特征的特征值,为第k个负类样本点的第i个特征的特征值。F值越大,说明此特征的辨别力越强。通常的做法是把特征按Fisher分数的大小进行排序,然后选择前N个特征进行后续的分类。
然而,具体选择多少个特征会达到最好分类效果,比较难以确定。为此,本文使用Fisher分数进行特征排序,然后使用FLDA和10折交叉验证选择最优的特征个数,得到最优特征组合,即最优特征子集。
2 实验结果与分析
2.1 实验数据
为了验证本文方法的有效性,共选取3个数据集进行试验,包括2个公开的BCI竞赛数据集和一个实验室自采集数据集。数据集的介绍如下:
数据集1:第4次BCI竞赛数据集IIa[21]。该数据集包含22个电极通道,采样率为250 Hz。9个健康被试(A01,A02,A03,A04,A05,A06,A07,A08,A09)分别执行左手、右手、脚和舌头4类运动想象任务。本文只对左手和右手2类任务进行分类。每个被试的训练集和测试集样本数均为144个。
数据集2:第4次BCI竞赛数据集IIb[22]。该数据集包含3个电极通道,分别为C3、CZ和C4,采样率为250 Hz。9个健康被试(B01,B02,B03,B04,B05,B06,B07,B08,B09)分别执行左、右手2类运动想象任务。该数据集有5个会话数据,本文只对第3个会话数据进行分析[23]。训练集和测试集的样本数均为80个。
数据集3:实验室的自采集数据。该数据集包含30个电极通道,采样率为250 Hz。6个健康被试(S01,S02,S03,S04,S05,S06)分别执行左、右手2类运动想象任务。使用Neuroscan公司的NuAmps 40导放大器以及脑电帽采集头皮脑电信号。
2.2 对比方法与参数设置
在数据实验中,参与对比的方法包括GA和二进制PSO(Binary PSO, BPSO),这2种方法的参数设置如下。
GA的参数设置与文献[24]一致。具体如下:特征编码方法使用二进制编码。适应度函数使用K-近邻分类器的分类准确率,其中k=5。种群个数为10,使用迭代次数作为算法的终止条件,最大迭代次数为100。交叉概率为0.8,变异概率为0.01。
BPSO的实现参考文献[25],参数设置与文献[25]一致。具体如下:适应度函数使用K-近邻分类器的分类准确率,其中k=5。种群个数为10,使用迭代次数作为算法的终止条件,最大迭代次数为100。加速系数c1=2,c2=2,最大速度和最小速度分别为6和-6,最大惯性权重和最小惯性权重为0.9和0.4。
为更加简明地描述实验结果,以下内容把基于LASSO的混合特征选择方法简称为LASSO_h,基于F-score的混合特征选择方法简称为F-score_h。
2.3 实验结果
表1~表3分别给出了数据集1~数据集3的分类准确率,表中最高分类准确率使用黑体加粗标注。F-score_h在数据集1中取得了最高的平均分类准确率,而LASSO_h在数据集2和数据集3中取得了最高的平均分类准确率。本文提出的2种混合特征选择方法都优于现有的特征选择方法。

表1 数据集1分类准确率/%
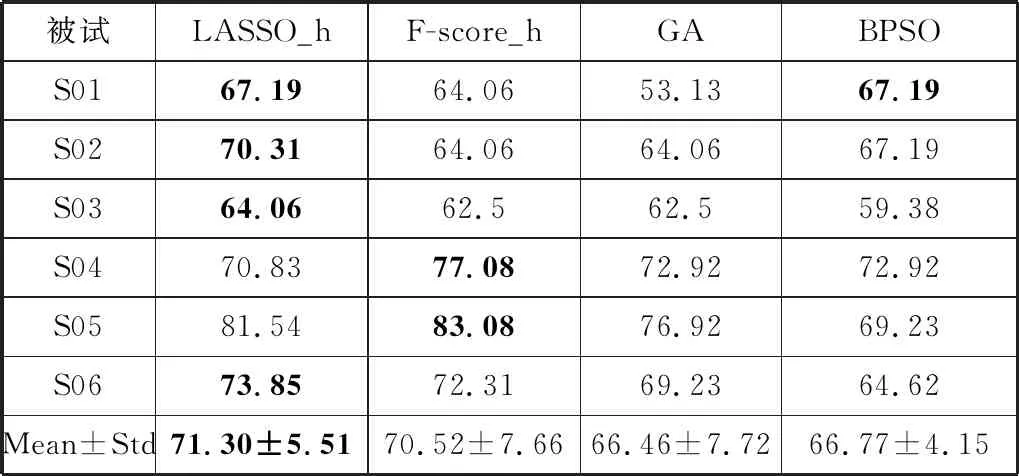
表3 数据集3分类准确率/%
为了更直观地比较不同特征选择方法的分类效果,图3给出了所有数据集的平均分类准确率对比情况。LASSO_h、F-score_h、GA和BPSO在所有数据集上取得的平均分类准确率分别为:74.87±14.03、75.12±15.03、72.08±14.35和72.42±13.64。F-score_h略高于LASSO_h,但LASSO_h在数据集2和数据集3的分类效果优于F-score_h。从数据集的适用性考虑,LASSO_h相比F-score_h有优势。
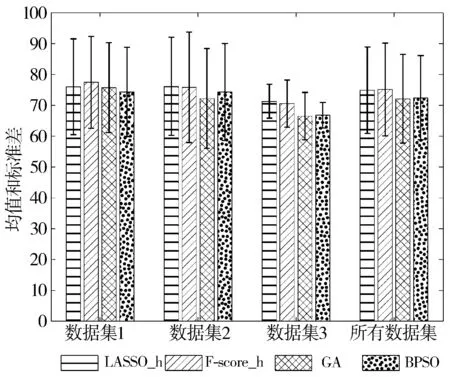
图3 不同算法下各个数据集的平均分类准确率
图4给出了不同特征选择方法分类准确率的整体分布情况。分类准确率的整体分布,LASSO_h和F-score_h这2种方法比较靠上,但是F-score_h的最小值低于40%,而LASSO_h方法的最小值在几种方法中表现最佳,说明LASSO的稳定性和鲁棒性会更好一些。
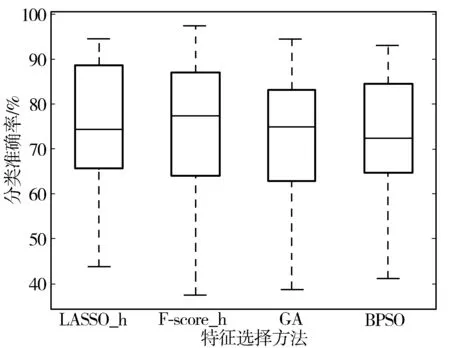
图4 不同算法下所有数据的分类准确率分布
表4给出了各种方法在模型训练阶段的特征选择时间,F-score_h的特征选择时间最少,LASSO_h多于F-score_h,但是远少于GA和BPSO。从特征选择时间角度考虑,基于过滤式的混合特征选择具有明显的时间优势,而基于智能优化的特征选择方法其计算时间都比较长。过滤式特征选择方法计算都比较简单,所以其特征选择时间比较少。在未来的工作中,可以加大对这方面的研究。

表4 各种方法的特征选择时间/s
3 讨 论
从以上实验结果的比较分析中可以得出结论:
1)从平均分类结果和特征选择时间方面评价,基于F-score混合特征选择方法优于基于LASSO的混合特征选择方法。
2)从各个数据集的分类效果和分类准确率整体分布评价,基于LASSO的混合特征选择方法的数据集适用性比较好,其稳定性和鲁棒性也较好。
导致基于LASSO的混合特征选择方法分类效果不佳的原因可能是出现了过拟合现象。该方法利用相同的训练集使用2次交叉验证选择最优的特征子集,容易出现过拟合现象。GA和BPSO的分类效果比较差,有多方面的原因。首先,遗传算法可能会出现陷入局部最优的情况;而BPSO可能会出现“早熟”现象[25]。另外,GA和BPSO的初始化参数选择对特征选择影响也非常大[26-27],如何选择更合适的模型参数是非常关键的问题。
综合考虑分类效果和特征选择时间,基于F-score的混合特征选择方法是一个较好选择。
4 结束语
本文提出了2种混合特征选择方法。第1种方法是LASSO嵌入式方法和包裹式方法的结合,第2种方法是Fisher分数过滤式方法和包裹式方法的结合。实验结果表明,无论是分类效果和特征选择时间,这2种方法都优于基于智能优化的包裹式方法。特征选择对运动想象脑电解码至关重要,在未来的工作中,将更加系统全面地研究特征选择方法,提出更具时效性的特征选择方法。

