基于多尺度CLG光流法的多目标检测方法

任朝宇，赵冬娥，张 斌，杨学峰，褚文博

(中北大学信息与通信工程学院，山西 太原 030051)

0 引 言

多目标检测[1]与人们的工作和生活息息相关，在医疗、工业质量检测、机器人跟踪导航、体育赛事、力学测试分析、智能交通、生物观察、影视特技及军事视觉制导等领域都有着极其广泛的应用[2]。

目前，静态场景下的动态目标检测方法主要有背景减除法、帧间差分法和光流法[3-5]。背景减除法[6-7]是将当前视频帧与建立的背景模型进行比较，通过判定灰度等一系列特征发生的变化或直方图等统计信息的变化来分割运动目标[8]，同时判断是否发生异常情况。它主要适用于静态、简单背景中的目标检测[9]。帧间差分法[7,10]是将多帧差分的图像信息进行融合，从而获得更好的结果[11]。其缺点是检测运动目标区域不完整，会丢失部分信息[12]。光流法[13-14]是利用图像序列中像素在时域上的变化和相邻帧之间的相关性来找到前一帧跟当前帧之间对应关系，从而计算相邻帧之间物体的运动信息的一种方法。其生成的光流场记录的是图像像素点灰度变化的瞬时速度场，它包含了物体的运动和结构信息[15-16]。而本文要检测的目标是处于运动中，携带运动信息的，在综合比较以上3种算法后，本文选取光流法对图像进行处理。

多目标检测场中背景比较复杂，影响检测的因素较多，传统的算法已经难以满足检测要求，而本文算法综合了Lucas-Kanade光流法[17-18]和Horn-Schunck光流法[19]的优点，使用2种光流方法结合的CLG(Combining Local and Global)光流方法并结合多尺度的方法对图像进行处理，既可保持光流场的分段平滑，又可提高算法对噪声的鲁棒性。

1 全局与局部组合CLG方法

光流[20]是空间运动物体在观察成像平面上的像素运动的瞬时速度。光流反映了图像的变化，包含目标运动的信息，可用来确定目标的运动。

1.1 亮度恒定约束方程

所有光流技术都是基于亮度恒定不变这个假设之上的，它们都可以利用图像亮度的时空导数。在图像中物体部分亮度守恒的条件下，基于图像平移的一阶导数有：

I(z,t)=I(z-vt,0)

(1)

其中，v=(u,v)T,z=(x,y)T,I(z,t)为t时刻像素点(x,y)的像素值(亮度)。

假设物体的运动较小，则利用式(1)的泰勒级数展开式，形成了一个亮度恒定约束方程：

Ixu+Iyv+It=0

(2)

其中，u=dx/dt,v=dy/dt,Ix=∂I/∂x,Iy=∂I/∂y,It=∂I/∂t。

Ix和Iy为亮度的空间变化率，即亮度在整个图像中的变化速度，表示在给定的像素点上，像素值随时间变化的速度。亮度恒定约束方程是光流技术的基本约束方程。

1.2 Lucas-Kanade局部方法

Lucas-Kanade(LK)方法[21-22]假定光流在ρ大小的邻近区域内是恒定的，通过最小二乘准则计算该邻域内所有像素的光流场：

ELK(u,v)=Gρ*(Ixu+Iyv+It)2

(3)

其中，Gρ表示大小为ρ的高斯核，*表示卷积。当(u,v)取得最小值且满足∂uELK=0、∂vELK=0时，可以得到以下矩阵方程：

(4)

如果图像梯度不为0，则系统的矩阵是可逆的，因此可以计算出唯一解。

LK光流法是局部平滑约束，只能得到特征点的光流结果。虽然LK光流法计算量小，能产生稳健的光流，但是很难精确地提取到运动目标的形状。

1.3 Horn-Schunck全局方法

假设I=I(x,y,t)为输入的图像序列，V为光流向量场，V=[u(x,y,t),v(x,y,t),1]T。Horn-Schunck(HS)算法模型假设图像总亮度水平随时间变化恒定，并且估计的光流向量在图像空间中平滑变化，亮度恒定假设由时间导数It=dI/dt表示，HS光流场[23]由一阶泰勒公式展开定义如下：

I(x+u,y+v,t+Δt)-I(x,y,t)=0

⟹Ixu+Iyv+It=0

(5)

将式(5)在图像域Ω上进行积分，能量函数定义为：

(6)

其中，Ix、Iy为空间导数，α(|∇u|2+|∇v|2)为光流场的平滑约束，V变化越大就越会导致|∇u|和|∇v|的增加。权重系数α>0为全局正则化系数，是光流场的平滑因子。α越大，场越均匀，而α越小，光流场的位移矢量越不均匀。

HS光流法可以产生密集的光流，但是HS方法对噪声更敏感，而本文的背景图像中噪声干扰比较严重，这大大降低了光流估计的精度。

1.4 全局与局部组合CLG方法

CLG[24]组合方法是在综合了LK和HS方法优点的基础上提出的，LK光流法可以产生稳健的光流，而HS光流法可以产生密集流场。使用CLG组合方法的目的是通过采用基于全局和局部方法的平滑项，产生对噪声具有鲁棒性的密集流场。

假设亮度梯度矩阵∇3I=[Ix,Iy,It]T，则HS光流场的能量函数如式(7)：

(7)

CLG光流场的能量函数在∇3I引入了一个平滑项，表达如式(8)：

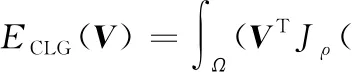
(8)

且有Jρ=Gρ*(∇3I∇3IT),Jρ为局部时空导数平滑项，表示为二维高斯核Gρ与矩阵∇3I∇3IT的卷积。如果ρ=0，则未发生局部平滑，CLG光流场相当于HS光流场；如果α=0，则该函数相当于LK光流场。

1.5 算法的优化

HS方法和CLG方法使用L2范数的平方，L2范数的缺点是对噪声很敏感。在复杂的检测场背景下，由于影响光流估算的干扰因素比较多，为了大大减少这些干扰因素带来的影响，将L2范数的平方改为L1范数，L1范数相对于L2范数对噪声没有那么敏感，对噪声具有更好的鲁棒性。因此CLG方法表达如下：

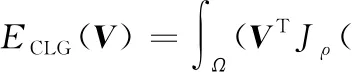
(9)

除了将L2范数的平方修改为L1范数外，在CLG算法的基础上，结合多尺度的思想，本文提出多尺度CLG方法对连续2帧图像做处理，实现光流场的估算，以提高算法对噪声的鲁棒性。

2 多尺度CLG方法

为了满足光流场的假设，HS方法和CLG方法对亮度恒定约束做了线性化，因此要求矢量场V较小。对于具有较大目标位移的图像序列来说，会存在问题：可能会出现目标不连续并导致检测错误的情况。由于图像中目标较多，可能会存在目标位移较大的问题。为了解决这个问题，本文提出多尺度的方案，采用由粗到细的方法依次计算更精确的光流向量场。

多尺度[25]的主要思想是计算一个图像金字塔[26]，对将要估计的光流场的集合中的每一幅图像进行降采样(一般为2帧，分别为I1和I2，时刻为t1和t2)，从最小的金字塔图像开始，计算向量场，然后为下一个较细的尺度，粗估计用于t2处使第2帧图像发生变化，表示为I(x+δV)，并计算出相应的光流向量场[27]。在金字塔的每一层都计算向量场增量(δV)，最终的光流向量场估计是所有金字塔层估计的插值和。多尺度CLG光流法可表示为：

α(|∇δu|+|∇δv|))dxdy

(10)

其中，δV=(δu,δv)。其算法原理如图1所示。

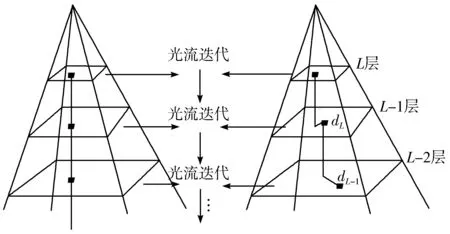
图1 多尺度光流算法原理图

多尺度算法工作流程如图2所示。

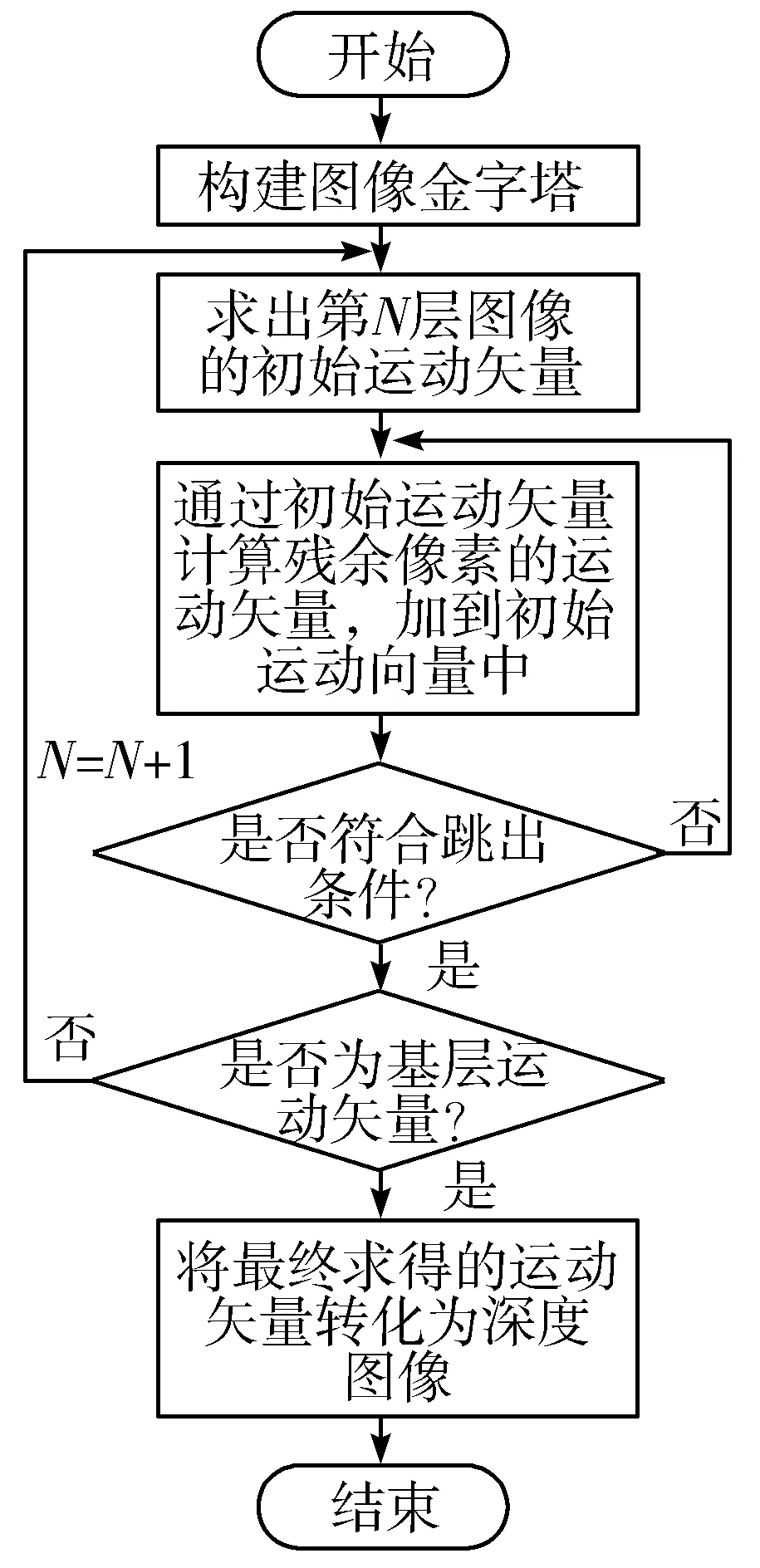
图2 多尺度光流算法流程图

3 实验与结果分析

为了验证算法的有效性，本文比较了CLG算法和多尺度CLG算法误差。光流误差评价采用平均角度误差AAE(Average Angular Error)和平均端点误差AEE(Average Endpoint Error)的误差估计方法来评估光流计算的精度。

平均角度误差AAE与平均端点误差AEE的计算公式如下：

(11)

(12)

其中，(uE,vE)表示光流场的速度估计值，(uT,vT)表示标准光流的真实值，n表示图像中像素点的个数。

实验1选取Middlebury标准光流库中的图像序列Urban2和Grove2作为测试图像序列，使用CLG算法和本文所提出的多尺度CLG算法对测试图像进行平均角误差AAE和平均端点误差AEE的误差计算，结果如图3所示。

(a) 原图 (b) True Flow

平均角度误差AAE和平均端点误差AEE的对比如表1所示。经过实验结果的对比与分析，可知本文所使用的多尺度CLG光流算法所得的光流的误差明显减小，提高了光流计算的精度。实验表明多尺度CLG算法结合了CLG算法和多尺度方法的优点，有效地解决了经典CLG算法存在的光照问题和噪声问题，具有较高的精度。

表1 平均角误差AAE和平均端点误差AEE对比

实验2选取一组多目标运动图像做CLG算法以及多尺度CLG算法处理，处理结果如图4所示。

(a) 原图连续帧1

可以看出，图4(c)与图4(d)都能很明显地显现出运动物体的形状，但与图4(d)相比，图4(c)中噪声明显，与图4(f)相比，图4(e)中噪点明显。由此可以得出多尺度CLG算法相对CLG算法对噪声的鲁棒性明显增强，光流估计整体效果较CLG算法有了很大的提升。

4 结束语

为了提高算法对噪声的鲁棒性，本文使用了CLG光流法并结合多尺度的方法，运用由粗到精的金字塔思想对图像进行处理，可提高光流的估计精度，并将L2范数的平方改为L1范数，以减小周围因素带来的干扰。通过Middlebury光流数据库图像光流计算结果和标准光流图像对比对所提出的方法进行验证，实验结果表明了所提方法的有效性。用所提方法对多目标图像进行处理，结果表明，多尺度CLG光流方法可以使光流场分段保持平滑，对噪声具有良好的鲁棒性。