基于多传感器两级特征融合的滚动轴承故障诊断方法

刘 仓， 童靳于， 包家汉， 郑近德， 潘海洋

(安徽工业大学 机械工程学院，安徽 马鞍山 243032)

滚动轴承作为旋转机械的关键部件，其运行状态直接影响到整个机械设备的性能。因此，如何有效地从滚动轴承的复杂振动信号中提取故障特征并进行模式识别，对保障旋转机械正常运行有重要的意义[1-2]。

对于非线性、非平稳的滚动轴承振动信号，传统的故障诊断大多是基于单一传感器信号开展的[3-4]。对于一个复杂的机械系统，单个传感器包含的故障信息有限，无法进行准确的状况监测和故障诊断[5]。多传感器信息融合技术是近年来发展起来的一种重要的应用技术，已被广泛应用于军事和民用领域[6]。与单传感器系统相比，利用多传感器信息融合技术可以提高诊断的精度、可靠性和鲁棒性[7]。文献[8]利用多传感器信息融合技术实现旋转机械的故障诊断，提取多个传感器振动信号的时域特征，构成融合向量，输入支持向量机进行分类。文献[9]为了更好地实现旋转机械的故障诊断，提出一种基于奇异值流形特征、优化支持向量机和多传感器信息融合的智能故障诊断模型。文献[10]提出了基于多类支持向量机数据融合的齿轮故障诊断方法，采用各种分析方法从振动信号中提取故障特征，将故障特征融合后输入支持向量机中。

多传感器信息融合的常用方法可分为两大类：以传统非线性数学为基础的方法和以深度学习为基础的方法。以传统非线性数学为基础的方法如：加权平均法[11]、卡尔曼滤波法[12]、多贝叶斯估计法[13]以及D-S证据推理法[14]，这些方法主要应用于数据级或决策级融合。以深度学习为基础的方法如：卷积神经网络 (convolutional neural network，CNN)[15]、深度置信网络 (deep belief network，DBN)[16]等具有强大的自组织映射和非线性处理能力的网络，能够满足多传感器数据融合的需求，通常用于高维数据特征级的融合。文献[17]通过在CNN中引入空洞卷积核实现多传感器数据的自适应融合，从而更好的实现了基于多传感器数据的故障诊断。文献[18]为了解决单传感器振动信号有用信息较少的问题，提出了一种基于多传感器振动信号和深度置信网络的新型故障诊断方法。利用DBN的学习能力，自适应地融合多特征数据，识别各种轴承故障。

然而，对于多传感器融合的故障诊断问题，目前尚未建立统一和有效的融合模型及算法，各种所提模型目前仍处于探索阶段。针对故障诊断中的多传感器融合问题，本文提出一种基于多传感器两级特征融合的故障诊断方法。首先，针对一维多传感器振动信号，在特征融合的第一阶段，利用变分模态分解(variational mode decomposition，VMD)[19]进行预处理，得到若干本征模态函数(intrinsic mode function，IMF)分量。其次，为了充分表示故障信息，对每个IMF分量提取时域、频域和多尺度熵特征，在一维特征层面融合后形成多域特征集。然后，为了进一步提升特征融合能力和网络诊断性能，提出一种改进的深度自编码网络(improved deep auto-encoder network，IDAEN)用于第二阶段的特征融合及分类。最后，设计不同工况下的滚动轴承故障诊断试验，验证了所提模型的优越性。

1 本文所提方法

在本章中，提出了一种基于多传感器信号的两级特征融合模型，并将其用于滚动轴承故障诊断。

1.1 多传感器信号两级特征融合模型架构

所提模型如图1所示。包括2个阶段特征融合：在第一阶段，首先通过VMD计算每个传感器振动信号的IMF分量，再根据各IMF分量分别提取时域、频域和多尺度熵特征，最后融合成一个多域特征集；在第二阶段，首先构建IDAEN，然后输入第一阶段融合的特征，利用IDAEN进一步进行特征的深度融合和分类。

图1 多传感器信息融合过程模型Fig.1 Multi-sensor information fusion process model

1.2 实施过程

1.2.1 第一阶段特征融合

第一阶段特征融合方案如下：

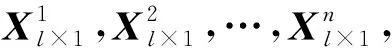
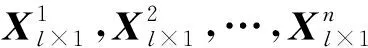
1.2.2 第二阶段融合及分类

自编码器(auto-encoder，AE)是一种能够最小化输入和输出重构误差的无监督神经网络[23]，分为编码器和解码器2个部分，其结构如图2所示。AE由3个全连接层组成，前两层构成编码器，后两层构成解码器。编码器将高维的输入数据转换为低维的特征表示，解码器将特征表示转化为输入数据的重构形式。

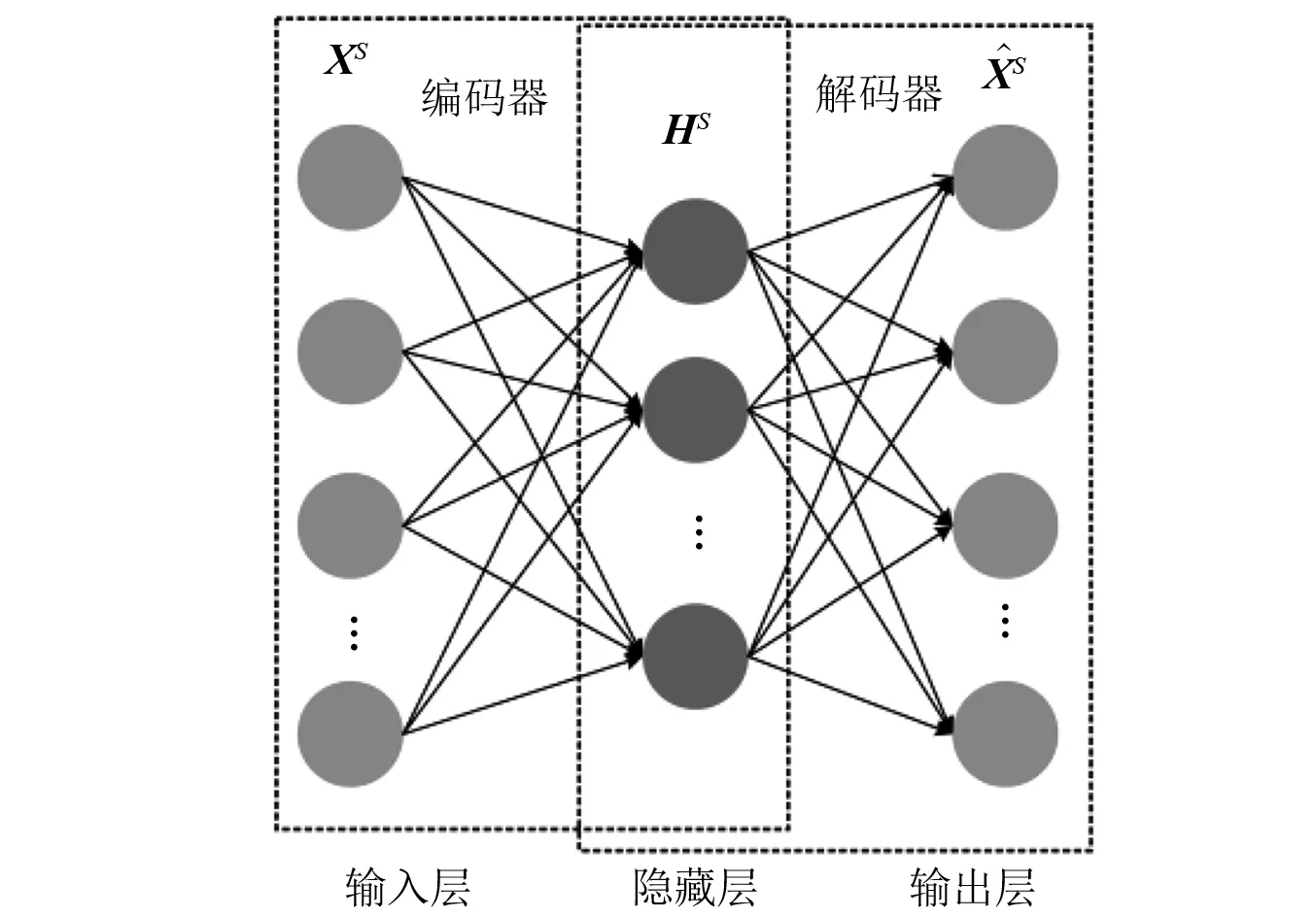
图2 AE的结构图Fig.2 Structure chart of AE

H=Sf(WX+b)

(1)

(2)

式中：W，W′分别为编码器和解码器的权重；b，b′分别为编码器和解码器的偏置；Sf，Sg分别为编码器和解码器的Sigmoid激活函数。

为了进一步提升多域特征融合能力和故障诊断性能，本文基于AE提出一种改进的深度自编码网络用于特征的第二阶段自适应融合与分类。IDAEN是通过堆叠多个改进自编码器(improved auto-encoder，IAE)和一个Softmax分类器组成，其结构如图3所示。

图3 IDAEN结构图Fig.3 Structure chart of IDAEN

如式(2)所示，通常标准AE模型采用Sigmoid作为激活函数，通过非线性映射输出隐藏层神经元。其定义为

(3)

由图4可知，Sigmoid函数在输入值非常小或非常大时，导数会变得很小，甚至接近于0，此时会出现梯度消失现象，模型学习效率和权重更新效率低。针对Sigmoid函数上述问题，本文采用Swish函数[24]作为IDAEN的激活函数，捕捉隐藏在多传感器信号中的精确映射关系。从图4可以看出，Swish函数在拥有Sigmoid函数全部优点的同时可以避免梯度消失现象，能够在非平稳输入和各种输出之间建立更精确的映射。其定义为

Swish(x)=x×Sigmoid(βx)

(4)

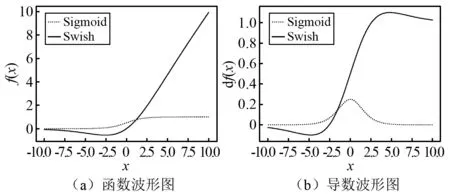
图4 Sigmoid和Swish的函数及导函数波形图Fig.4 Function and derivative waveforms of Sigmoid and Swish

Swish函数激活后，IDAEN隐藏层的输出为

(5)

式中：wij为第L层节点i与第L+1层节点j间的连接权值；bj为隐藏层节j点的偏置；β为常数。

标准AE模型中最常用的损失函数为均方误差(mean square error，MSE)。其定义为

(6)

对于信号中的异常值，MSE在计算过程中会赋予较大的权重，导致MSE对异常值的鲁棒性差。此外，MSE在远离最优点时损失增大，而当损失较小时梯度又变得很小。考虑到轴承振动信号中通常包含较多异常值，为了进一步提升所提IDAEN性能，本文采用log(cosh)[25]作为损失函数。log(cosh)拥有MSE的优点且对异常值的鲁棒性更好，在最优点附近的梯度会随着误差减小而减小，更有利于收敛。其定义为

(7)

更进一步，IDAEN的损失函数可以表示为

(8)

式中：第一项为均方误差损失；第二项为惩罚项；r为稀疏惩罚系数。

(9)

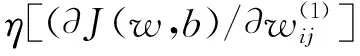
1.3 基于IDAEN的滚动轴承故障诊断流程

基于IDAEN模型的故障诊断流程如图5所示，具体步骤如下：

步骤1利用多个传感器采集滚动轴承振动信号；

步骤2 对多传感器数据进行第一阶段特征融合；

步骤3 根据一定比例，将第一阶段融合的多域特征集划分为训练集和测试集；

步骤4 进行第二阶段特征融合，构建IDAEN模型，初始化IDAEN模型的参数，使用训练集作为模型的输入，并最小化模型损失函数；

步骤5 将测试集输入到训练后的IDAEN模型中，获得测试精度。

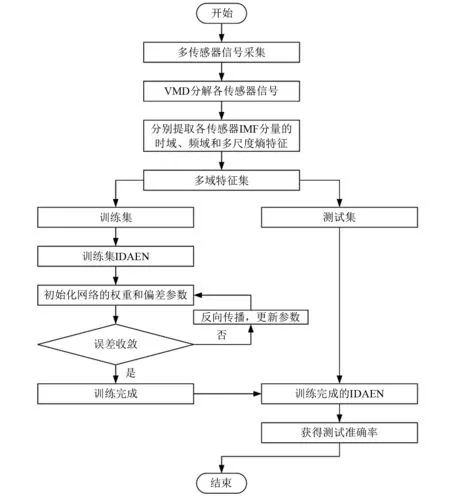
图5 IDAEN的故障诊断流程图Fig.5 Diagnosis flow chart for IDAEN

2 试验验证

2.1 滚动轴承试验台

自制滚动轴承模拟故障试验台如图6所示，包括电动机、加载装置、待测轴承等。待测滚动轴承型号为6206-2RS1 SKF，利用线切割技术在轴承内、外圈和滚动体上加工出不同故障程度的故障，四种健康状态如图7所示。试验中多传感器信号由3个不同方向的加速度传感器采集。

图6 滚动轴承故障试验台示意图Fig.6 Schematic diagram of rolling bearing test rig

图7 滚动轴承的不同健康状况Fig.7 Different health states of rolling bearing

2.2 滚动轴承多传感器信号

2.2.1 试验一：恒定转速

在负载5 kN，采样频率8 192 Hz，转速900 r/min的工况下，利用3个不同方向传感器分别采集不同故障程度的滚动轴承振动信号。3个不同方向滚动轴承振动时域信号如图8所示，各方向信号均包含滚动轴承六种健康状态：一类正常状态(NO)；两类内圈故障，故障深度分别为0.3 mm(IR1)和0.4 mm(IR2)；两类外圈故障，故障深度分别为0.2 mm(OR1)和0.3 mm(OR2)；一类滚动体故障，故障深度为0.2 mm(BA)。

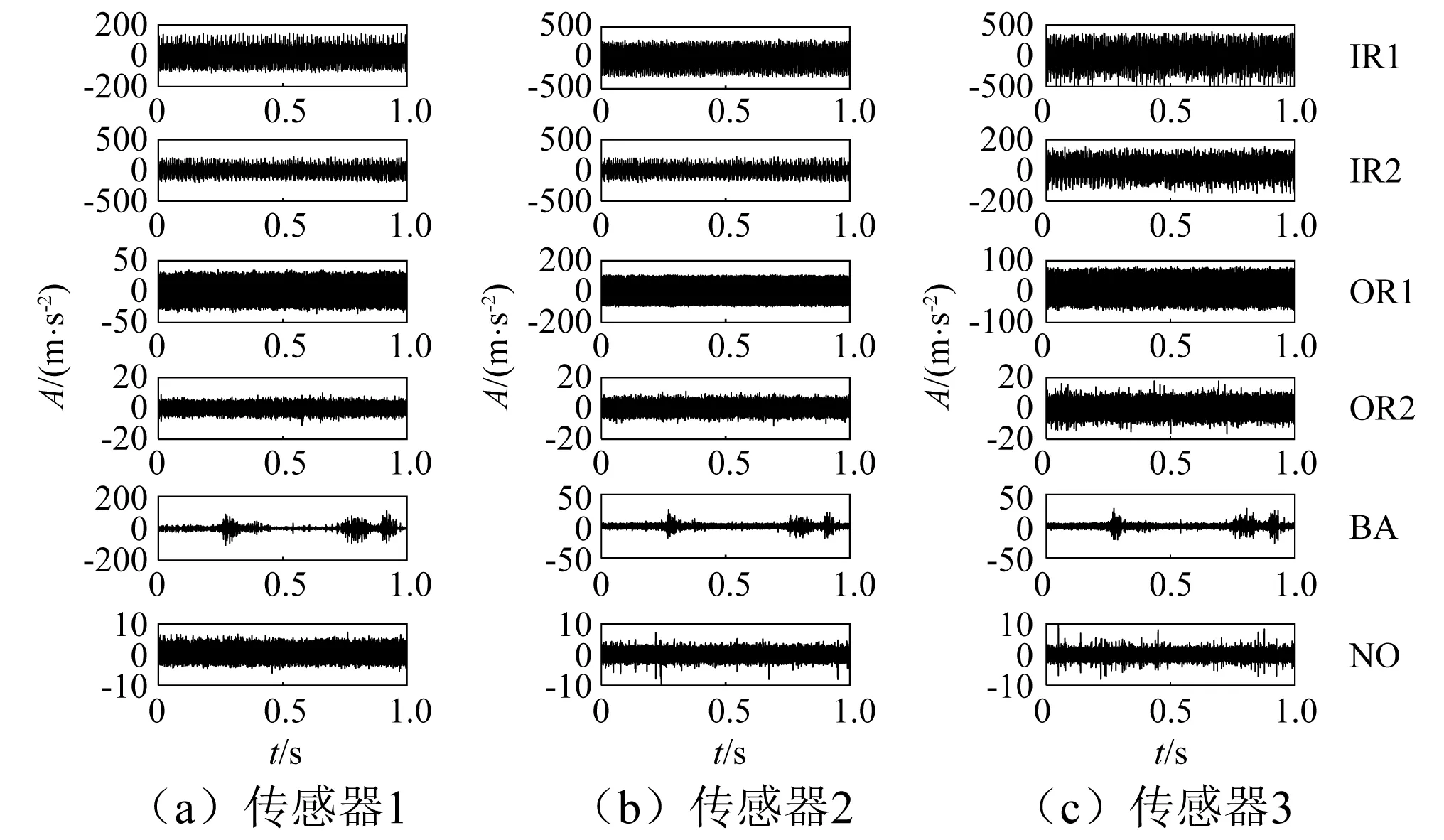
图8 恒定转速工况下滚动轴承3个不同方向振动时域信号Fig.8 Time domain signals of rolling bearing vibration in three different directions under constant speed

2.2.2 试验二：变转速

在负载5 kN，采样频率10 240 Hz，转速从500 r/min经过20 s加速至1 000 r/min的工况下，利用3个不同方向传感器采集不同健康状态的滚动轴承振动信号。图9为变转速工况下3个不同方向滚动轴承振动时域信号，包含六种健康状态：一类滚动轴承正常状态(NO)；两类内圈故障，故障的深度分别为0.3 mm(IR1)和0.4 mm(IR2)；两类外圈故障，故障深度分别为0.2 mm(OR1)和0.3 mm(OR2)；一类滚动体故障，故障深度为0.4 mm(BA)。

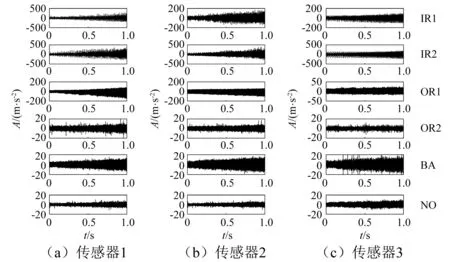
图9 变转速工况下滚动轴承3个不同方向振动时域信号Fig.9 Time domain signals of rolling bearing vibration in three different directions under variable speed

2.3 数据集构造

2.3.1 试验一数据集

选取负载5 kN，采样频率为8 192 Hz，转速900 r/min工况下的振动数据。在同一故障类型下，以1 024个数据点作为一个样本，每类故障随机取100个样本，共600个样本。利用VMD对每个样本分解得到3个IMF分量，对每个IMF分量提取12个时域特征，5个频域特征，以及5个多尺度熵值。因此，经过第一阶段特征提取，一个1 024个数据点的样本变为66个数据点的样本，并依此作为第二阶段IDAEN模型和对比模型的输入。随机将其中的90%划分为训练集，10%划分为测试集，如表1所示。每类故障获得了数据维度为90×66的训练样本，10×66的测试样本。在一维特征层面融合后，多传感器信号的每类故障获得了数据维度为90×198的训练样本，10×198的测试样本。

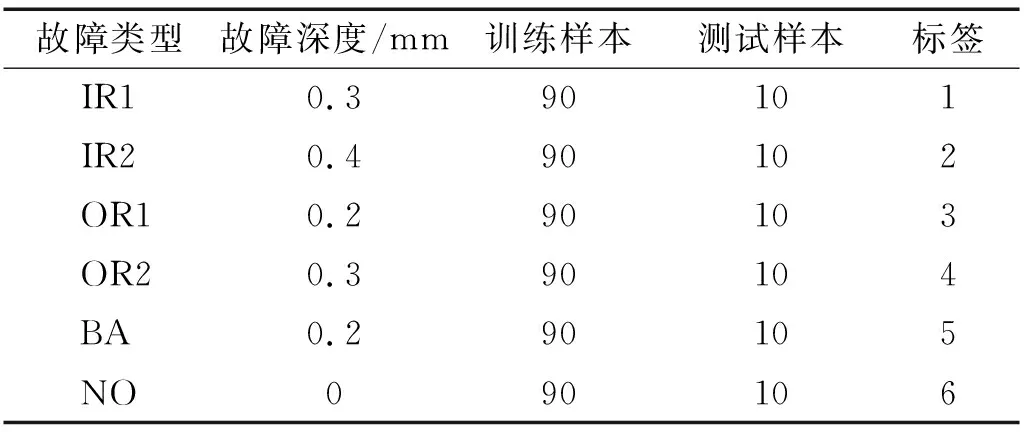
表1 试验一轴承数据集

2.3.2 试验二数据集

同样地，选取负载5kN，采样频率10 240 Hz，转速从500 r/min经过20 s加速至1 000 r/min工况下的振动数据。在同一故障类型下，以1 024个数据点作为一个样本，每种故障随机取200个样本，共1 200个样本。利用VMD对每个样本分解得到3个IMF分量，对每个IMF分量提取12个时域特征，5个频域特征，以及5个多尺度熵值。因此，经过第一阶段特征提取，一个1 024个数据点的样本变为66个数据点的样本，并依此作为第二阶段IDAEN模型和对比模型的输入。随机将其中的90%划分为训练集，10%划分为测试集，如表2所示。每类故障获得了数据维度为180×66的训练样本，20×66的测试样本。在一维特征层面融合后，多传感器信号的每类故障获得了数据维度为180×198的训练样本，20×198的测试样本。

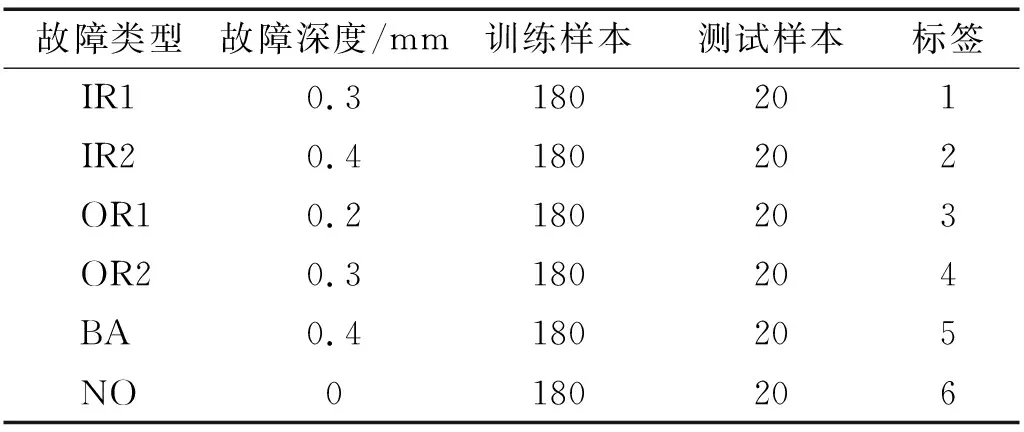
表2 试验二轴承数据集

2.4 对比试验和结果分析

2.4.1 多传感器信号协同诊断的可行性与有效性

为了减小随机误差，将试验一和试验二数据集的训练样本分别用IDAEN模型训练10次，再用测试样本进行测试，最后得到相应的诊断结果。根据文献[26]和多次试验，设置基于单个传感器信号的IDAEN结构为[66，50，30，10，6]，基于多传感器信号的IDAEN结构为[198，50，30，10，6]。设置IDAEN初始学习率为0.01，最大迭代次数为100，稀疏参数为0.01，稀疏惩罚系数r为0.13。

图10给出了两组试验10次测试的诊断准确率，表3和表4分别为两组试验10次测试诊断准确率的平均值和标准差。由表3可知，对于试验一数据集，基于多传感器融合的诊断准确率达到98.92%，标准差为0.416，相对于单个传感器1～传感器3来说，诊断准确率分别提高了4.67%，9.89%和5.09%。由表4可知，对于试验二数据集，基于多传感器融合的诊断准确率均达到96.49%，标准差为0.396，相对于单个传感器1～传感器3来说，诊断准确率分别提高了22.97%，3.53%和7.47%。综合多传感器信号协同诊断在两个不同数据集中的表现可以看出，基于多传感器融合信号的诊断效果远远优于单个传感器，充分证明多传感器信号协同诊断是可行的、有效的，且具有更好的鲁棒性。

图11和图12分别为两次试验中基于多传感器和基于单个传感器1～传感器3的混淆矩阵，其中横轴和纵轴分别是真实标签和预测标签。由图11可以看出，对于试验一数据集中故障类型IR2来说，基于传感器1信号的诊断准确率较低，仅为70%；基于传感器2和传感器3的诊断准确率相对较高，达到80%；而基于多传感器的诊断准确率取得了90%的诊断准确率。由图12可以看出，对于试验二数据集中故障类型NO来说，基于传感器3的诊断准确率较低，仅为55%；基于传感器1和传感器2的诊断准确率分别达到75%和85%；而基于多传感器的诊断取得了90%的诊断准确率。由此可知，对于同一故障，不同的传感器信号能够提供不同的故障信息，当它们协同诊断时，会提供更加准确和可靠的结果。

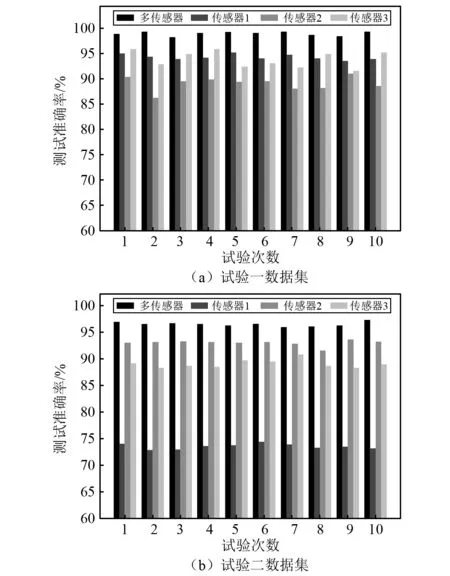
图10 不同传感器的10次对比试验结果Fig.10 Comparison of 10 experiment results for different sensors

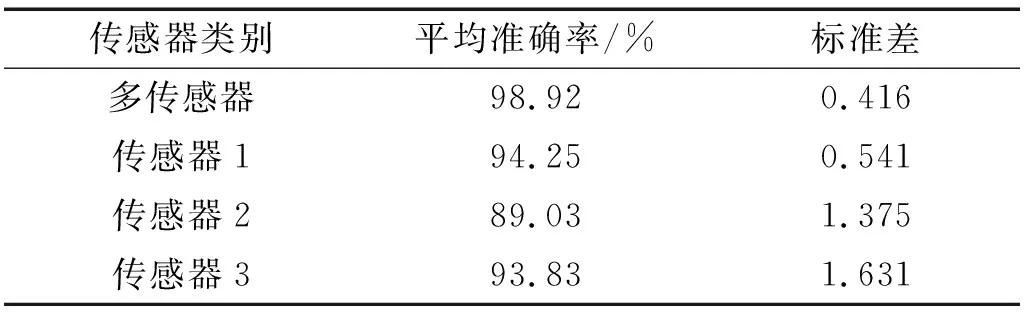
表3 试验一数据集中不同传感器信号的平均准确率和标准差

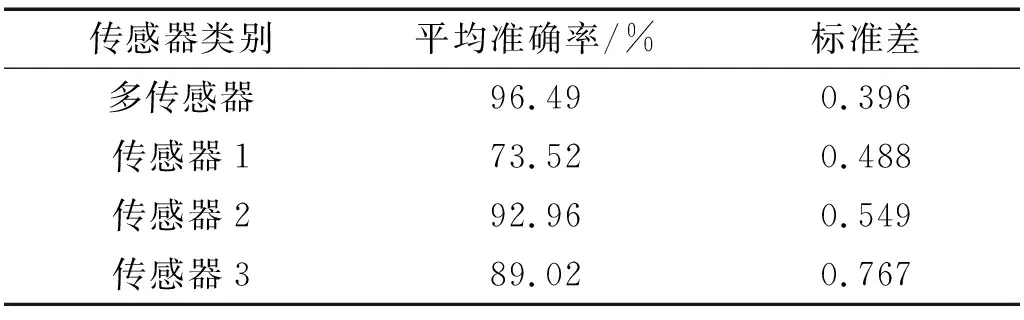
表4 试验二数据集中不同传感器信号的平均准确率和标准差

2.4.2 试验一结果及分析

为了验证所提模型的优越性，基于试验一数据集，将所提方法与深度自编码网络(deep auto-encoder network，DAEN)，堆叠稀疏自编码器(stacked sparse auto-encoder，SSAE)以及传统的机器学习模型[27]随机森林(random forest，RF)，支持向量机(support vector machine，SVM)进行比较。IDAEN与DAEN的超参数设置同2.4.1节，DAEN的激活函数和损失函数分别为Sigmoid和MSE。SSAE的网络结构与本文所提方法相同，为[198，50，30，10，6]，SSAE中的稀疏参数设置为0.2，稀疏惩罚系数设置为0.15。RF的最大深度设置为3，包含200棵树。SVM的核函数采用RBF函数，惩罚因子与核函数参数分别设置为1和0.01。

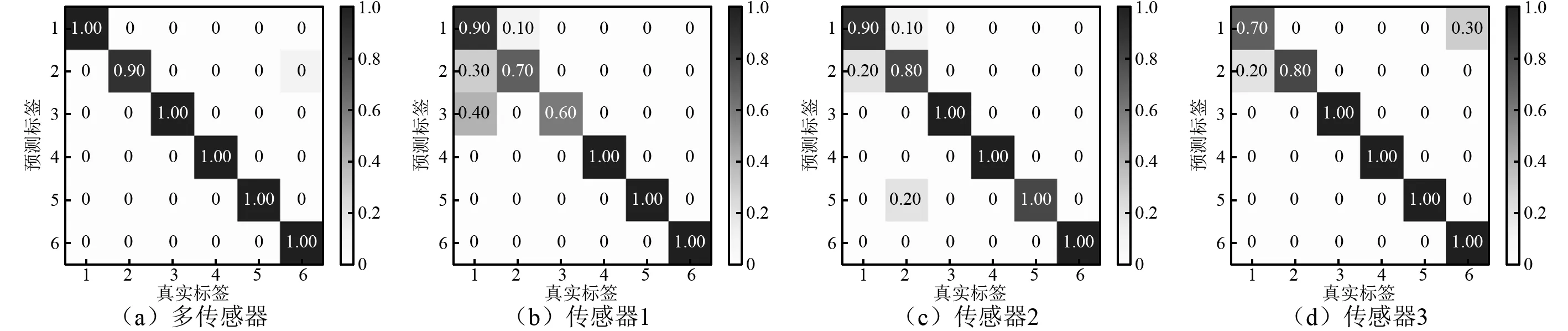
图11 试验一不同传感器信号的IDAEN混淆矩阵Fig.11 IDAEN confusion matrix for different sensor signals of experiment 1

图12 试验二不同传感器信号的IDAEN混淆矩阵Fig.12 IDAEN confusion matrix for different sensor signals of experiment 2

为消除偶然误差的影响，每种方法各进行10次试验，将10次试验诊断准确率的平均值和标准差作为该方法的评估指标。10次试验结果对比如图13所示，10次试验平均准确率和标准差如表5所示。

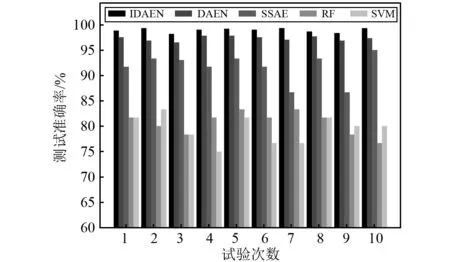
图13 试验一结果比较Fig.13 Comparison of experimental 1 results

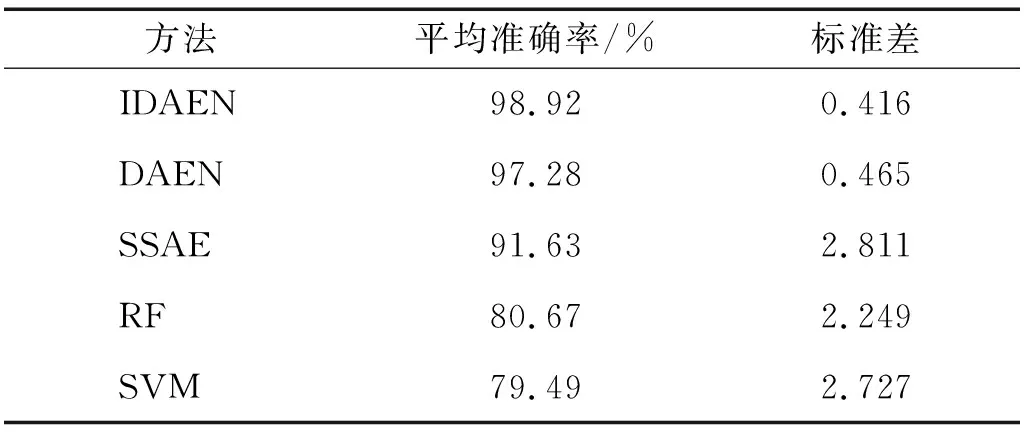
表5 对比模型的平均准确率和标准差

从图13和表5可以看出，在五种模型中，作为传统的机器学习算法，RF和SVM的10次试验诊断结果较其余三种自编码网络均偏低，平均准确率仅达到80.67%和79.49%，标准差分别为2.249和2.727，说明传统机器学习模型在处理滚动轴承信号时特征提取能力弱、模型泛化性能低，很难取得较好的诊断结果。在三种自编码网络中，SSAE的10次试验平均准确率最低，仅为91.63%，标准差为2.811，说明SSAE其深度不足以处理复杂的振动信号，且10次试验准确率波动较大，表现不稳定。DAEN模型的平均准确率为97.28%，标准差为0.465。所提IDAEN模型10次试验诊断准确率均最高，平均准确率达到98.92%，且标准差远低于所对比的其他几种模型，仅为0.416，说明了基于Swish激活函数和log(cosh)损失函数构建IDAEN的模型，能够较好地减少重构误差，提高模型的诊断准确率和稳定性。

为了进一步分析IDAEN的故障诊断效果，利用t-分布邻域嵌入(t-distribution stochastic neighbor embedding，t-SNE)算法[28]进行特征可视化，采用t-SNE方法分别对原始数据，所提方法Softmax层输出的特征绘制散点图如图14和图15所示。从图中可以看出，原始时域信号包含过多冗余信息，所有类别的特征难以分辨。而IDAEN在Softmax层提取到的特征较原始信号容易区分，表现出较好的分类效果，即相同的故障特征按照同一中心聚集，不同的故障特征被区分开，证明IDAEN网络性能较好。

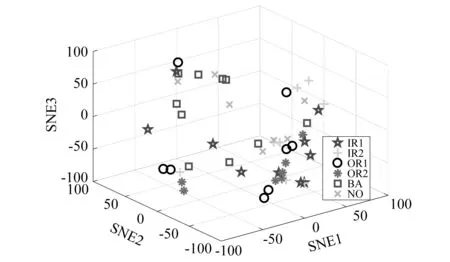
图14 原始信号的特征可视化Fig.14 Visualization of raw signal features

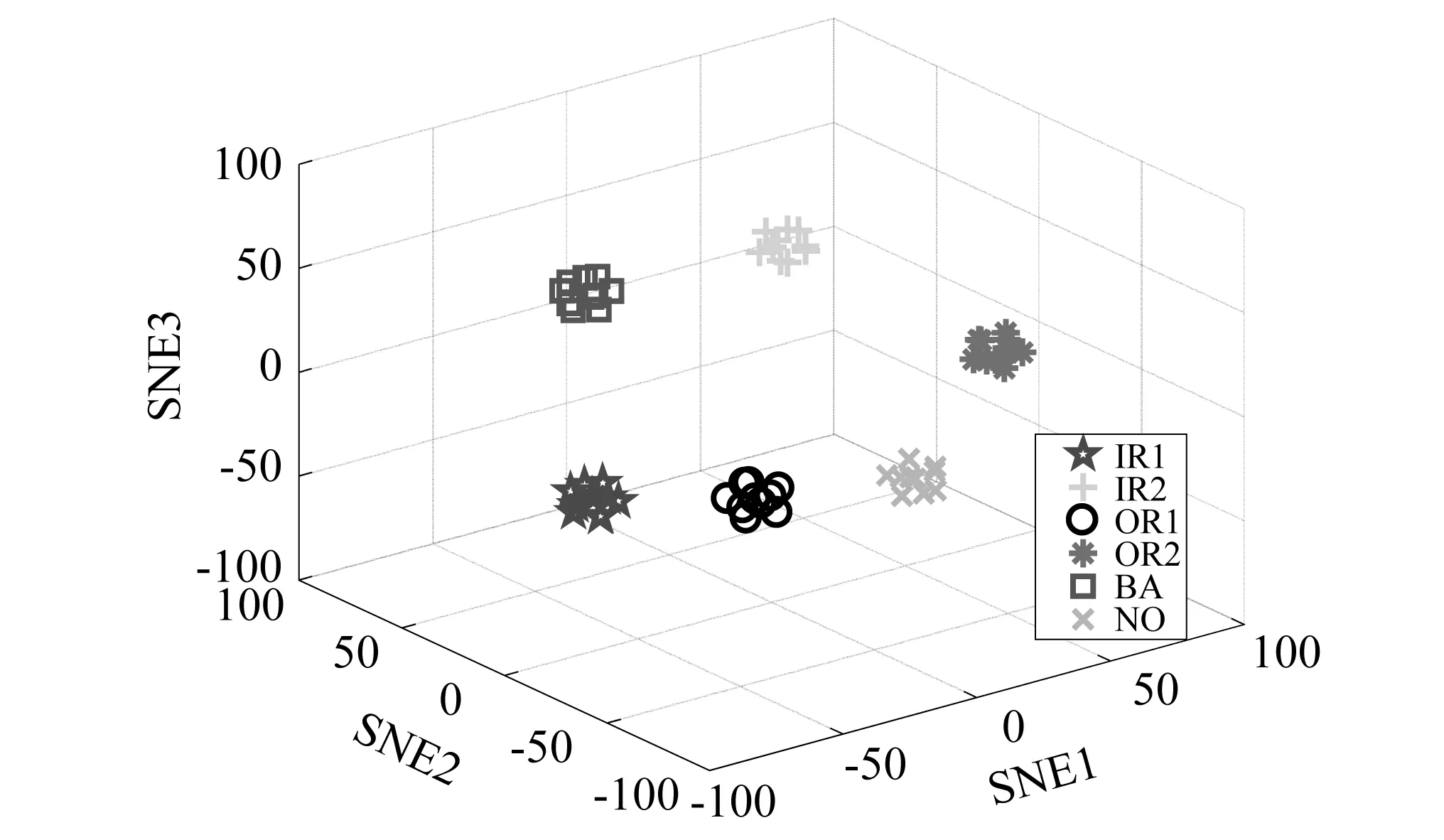
图15 Softmax层的特征可视化Fig.15 Visualization of Softmax layer features

2.4.3 试验二结果及分析

为了进一步验证所提模型对变转速条件下滚动轴承故障的诊断能力，基于试验二变转速数据集，将所提方法与DAEN，SSAE以及传统的机器学习模型RF，SVM进行比较。网络超参数的设定与2.4.2节相同。为消除偶然误差的影响，每种方法各进行10次试验，将10次试验诊断准确率的平均值和标准差作为该方法的评估指标。10次试验结果对比如图16所示，10次试验平均准确率和标准差如表6所示。

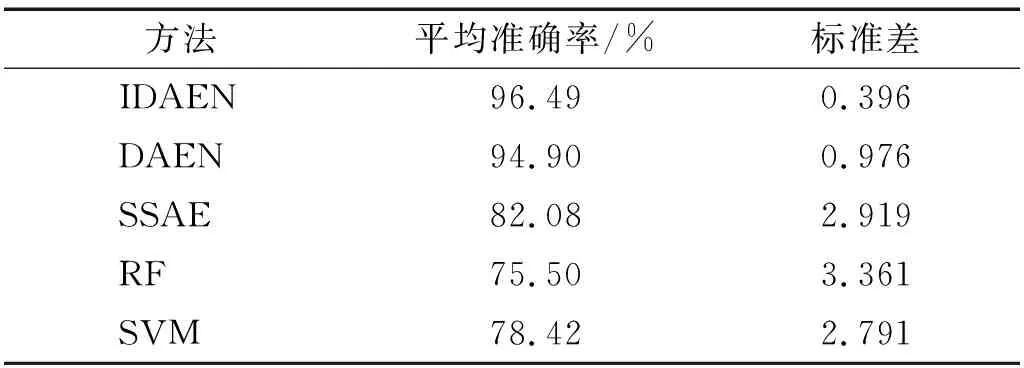
表6 对比模型的平均准确率和标准差

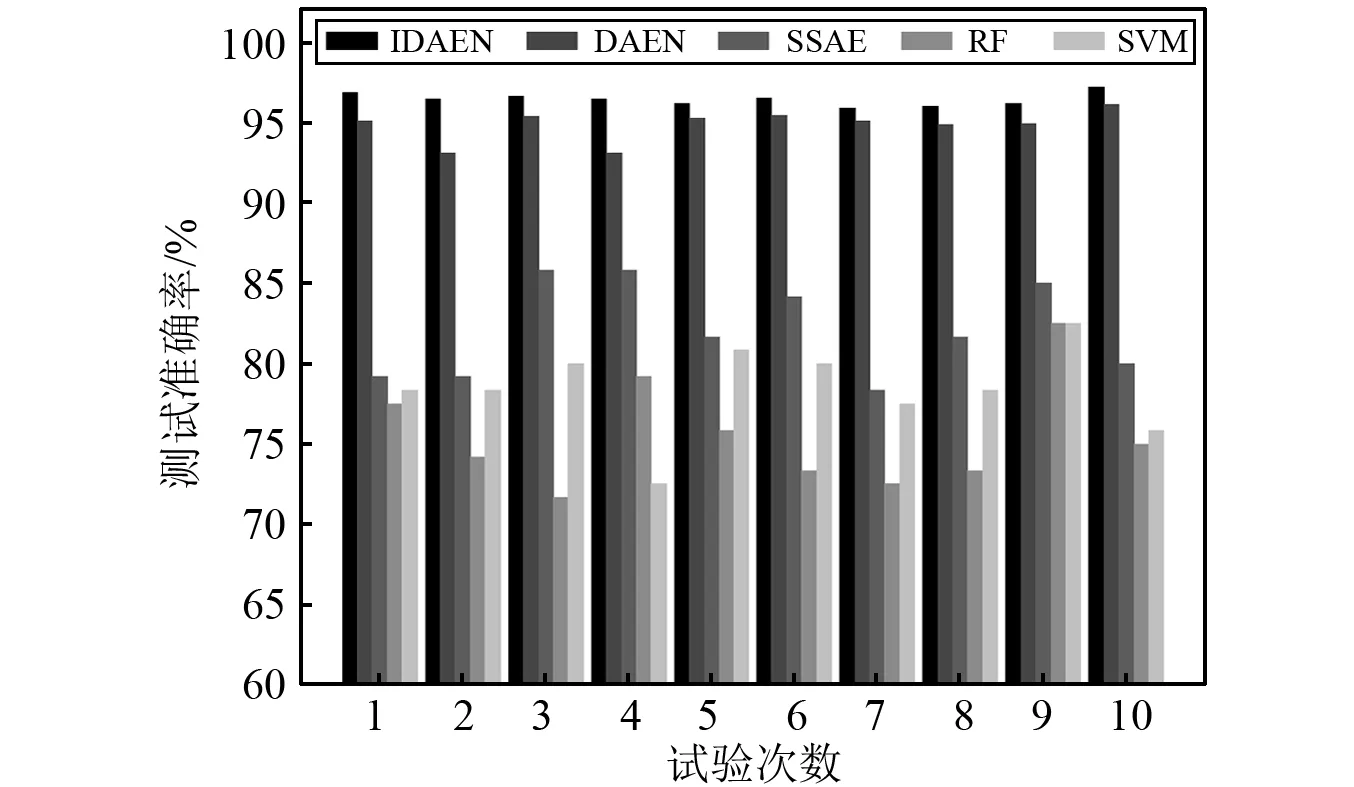
图16 试验二结果比较Fig.16 Comparison of experimental 2 results

对比表6和表5可知，五种模型故障识别准确率和模型稳定性均有不同程度的下降。由此可知，对于变转速滚动轴承振动数据的故障诊断问题，由于转速变化导致不同健康状态下振动信号特征差异变大，诊断难度加大，但所提IDAEN诊断准确率下降相对较少，体现了模型更好的鲁棒性。

从图16和表6可以看出，在五种模型中，RF和SVM作为传统的机器学习算法，10次试验诊断结果较其余三种自编码网络低，平均准确率仅达到75.5%和78.42%，标准差分别为3.361和2.791，说明传统机器学习模型在处理变转速滚动轴承信号时由于振动信号特征差异大，很难得到较好的诊断结果。在三种自编码网络中，SSAE的10次试验平均准确率较低，仅为82.08%，标准差为2.919，说明SSAE在处理变转速振动信号时诊断能力不足，且10次试验准确率波动较大，表现不稳定。DAEN模型的平均准确率为94.9%，标准差为0.976。所提IDAEN模型10次试验诊断准确率均最高，平均准确率达到96.49%，且标准差仅为0.396，说明了IDAEN模型针对变工况下滚动轴承的故障诊断仍然能够取得较高的试验准确率。

与试验一相同，采用t-SNE方法分别对原始数据，所提方法Softmax层输出的特征绘制散点图如图17和图18所示。从图中可以看出，原始时域信号所有类别特征的聚类效果很差。而IDAEN在Softmax层提取到的特征较原始信号容易区分，表现出较好的聚类效果，即相同的故障特征按照同一中心聚集，不同的故障特征被区分开，虽然有少数故障类型被错分，但不难证明IDAEN在变转速下的滚动轴承数据也能达到较高的识别精度，具有较好的鲁棒性。

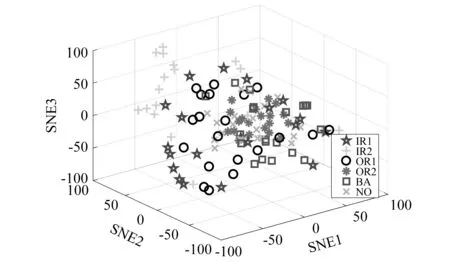
图17 原始信号的特征可视化Fig.17 Visualization of Raw Signal Features

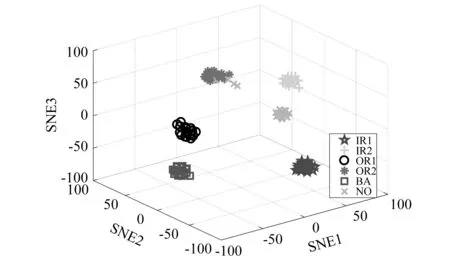
图18 Softmax层的特征可视化Fig.18 Visualization of Softmax layer features

3 结 论

本文提出一种基于多传感器两级特征融合的滚动轴承故障诊断方法，在不同工况下的轴承故障诊断数据集中表现良好，主要结论如下：

(1)本文所提基于多传感器融合的故障诊断方法诊断效果优于单个传感器，表现出更好的鲁棒性；两阶段特征融合为故障信号深度挖掘提供了更为有效的手段。

(2)基于Swish激活函数和log(cosh)损失函数设计的IDAEN显著提升了自编码器的性能。

(3)对于不同工况下的滚动轴承数据集，所提方法均取得了较高的识别率，特别是针对变转速工况，所提方法仍然具有较高的诊断精度。