考虑侧壁影响的偏心单刚体地震响应分析

贾传果， 潘家富， 李建广， 马 丽

(1. 重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045；2. 重庆大学 土木工程学院，重庆 400045)

地震时建筑物内高大器物的摇摆、晃动，通常会导致一定的人员伤亡和经济损失。据统计调查，室内家具带来的灾害损失仅次于建筑倒塌，其中以柜类家具的灾害形态最为多样[1]。柜体、冰箱等一般是靠墙壁安放在室内地面上，与地面或墙体之间没有可靠的连接。当建筑遭遇地震影响时，此类家具会发生摇摆、滑移、与墙壁碰撞等运动[2]，甚至会出现倾倒现象。

自1963年Housner首次提出了刚体摇摆动动力分析方法并创建了摇摆刚体经典模型后，刚体摇摆运动分析方法和模型得到了很大的发展与改进[3]。近年来，国外学者对偏心单刚体碰壁、碰地等运动做了许多理论性研究。Pompei等[4]研究了刚体块结构受强烈水平地面激励作用下的滑动与摇摆响应。Boroschek等[5]对在水平方向上有偏心的刚体块结构的动力响应特征进行了研究。Contento等[6]研究了偏心单刚体的偏心距和安全挡块对结构动力响应的影响。Wittich等[7]对偏心单刚体进行了试验研究，发现水平质量偏心对处于摇摆模式的结构影响最大，并可能增加倾覆的风险。现有研究主要是理论分析和数值模拟，试验研究相对较少，且未见有考虑碰壁的影响。建筑物内家具一般是靠墙放置的，发生碰壁后，会导致地震能量向刚体临空侧(与临墙侧对应的另一侧)积累，从而加剧刚体倾倒的危险性。另外，刚体在碰地前后，运动方程发生改变，若未能准确地判断碰撞点会导致误差积累，以致计算精度大幅降低。随着刚体摇摆运动研究的深入与非结构构件抗震的需要[8]，建立切合实际的刚体摇摆运动分析方法，提高刚体地震响应分析的精度显得尤为重要。

于此，本文首先利用Lagrange定理建立了偏心单刚体运动方程；并基于角动量守恒进行刚体碰撞分析，提出碰地瞬间的恢复系数公式，采用Rosenbrock方法建立了偏心单刚体摇摆运动响应分析方法；进行了刚体的单侧碰壁试验，验证了刚体动力分析方法的可靠性；通过数值模拟，分析了考虑碰壁影响的必要性。

1 偏心单刚体摇摆运动方程的推导

在推导运动方程的过程中，借鉴Housner的推导过程[9]，采用了如下假设：物体和地面均为刚体；物体与地面的接触面摩擦力足够大，不会产生滑动；碰撞是非完全弹性碰撞。

本文采用拉格朗日方程推导出偏心单刚体的摇摆运动方程。偏心单刚体的计算模型如图1所示，其中c″为矩形刚体的质心，质心到几何中心c的距离为偏心距(沿X轴正方向为正)e，e=B/2-b1。R1和R2分别为质心到摇摆点O和O′的距离。假定偏心单刚体绕O点摇摆运动时，摇摆角为正；相反，偏心单刚体绕点O′摇摆时，摇摆角为负。

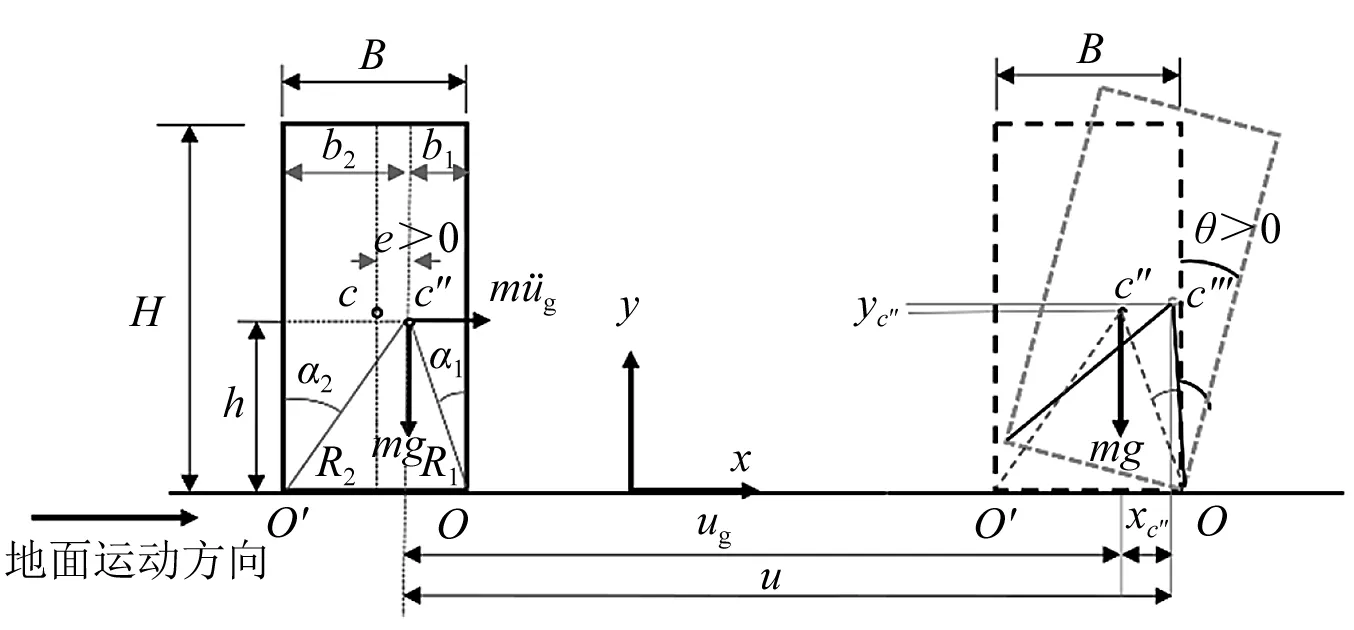
图1 偏心单刚体的计算模型Fig.1 Computational model of asymmetric rigid block

拉格朗日运动方程是一个非常重要的力学分析方程，它具有以下形式

(1)

式中：T为动能；Qk为广义力。该方程组以N个广义坐标，q1,q2,…，qN,作为独立变量。如果作用在质点系上的主动力都是有势力(保守力)，则广义力Qk可写成用质点系势能表达的形式

(2)

式中，V为系统势能。

假设地面运动位移为ug，假设刚体的摇摆角为θ。刚体质心在水平方向上的绝对位移为u可表示为

u=ug+xc″,xc″=b1-R1sin(α1-θ)

(3)

质心在竖直方向上的绝对位移为yc″可表示为

yc″=R1[cos(α1-θ)-cosα1]

(4)

对式(4)求导可得水平方向和竖直方向的绝对速度，依次求出偏心单刚体结构的动能T和势能V，根据拉格朗日方程可推得偏心单刚体绕O点摇摆运动方程。

(5)

同理矩形偏心单刚体绕O′点的摇摆运动方程

(6)

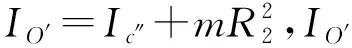
2 摇摆启动条件分析

当地面运动幅度较小时，结构不会产生摇摆运动。为提高计算效率，需要先判断是否发生摇摆，一旦发生摇摆则开始积分，故有必要分析刚体摇摆的启动条件。通过分析可得偏心单刚体发生摇摆运动应该满足两个条件：①摩擦力足够大，不产生滑动；②外部激励产生的力矩超过自重产生的恢复力矩。

当矩形偏心单刚体摆动(即θ>0)时，其自重产生的恢复力矩为mgRsin(a1-θ)。当摇摆角为零时，刚体自重产生的恢复力矩最大为mgRsina1。随着摇摆角增大，自重产生的恢复力矩减小，当摇摆角达到临界值(即θ=α1)时，自重产生的恢复力矩为零[10]。一旦摇摆角超过临界值，刚体无法回到初始平衡位置，即产生倾覆。刚体摇摆时，恢复力矩和摇摆角遵循图2所示关系，在此过程中不损失能量[11]。刚体摇摆运动的能量损失主要来源于摩擦耗能和单刚体与地面的碰撞耗能。

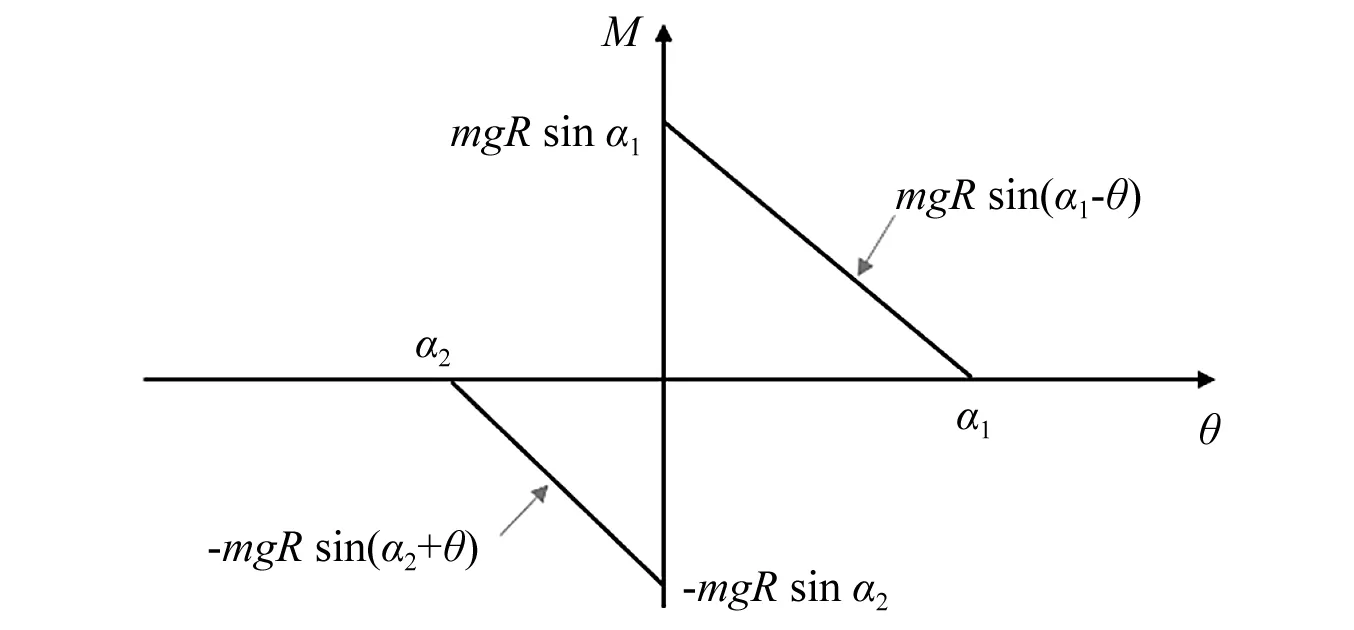
图2 恢复力矩与摇摆角关系Fig.2 Relationship of restoring moment and rocking angle

如图1所示，当地面运动引起的惯性力绕O点的力矩超过自质量产生的恢复力矩，刚体开始摆动。由此可见，偏心单刚体绕O点摇摆运动的启动条件为

(7)

同理可以得到绕O′点的摇摆运动条件

(8)

对比式(7)和式(8)可以看出，偏心的矩形单刚体对不同摇摆点的摇摆启动条件不一致，以靠近质心的角点为摇摆点的摇摆运动更容易被激发。

当地面运动幅值较小时，不会激起刚体的摇摆运动。这样可把地震动时程曲线中第一次达到启动条件之前的部分扣除掉。另外，一般地震动时程曲线尾部，幅值小于启动条件时，不会引起过大的摇摆运动。因此，可以把地震动时程曲线中最后一次达到启动条件之后的部分扣除掉。

3 理想条件下碰撞恢复系数的确定

碰撞是刚体摇摆运动的关键，其特点是在短时间内速度大小和方向发生瞬时变化。碰撞问题也一直是动力学领域的难点和热点问题[12]。碰撞问题的关键是碰撞恢复系数，关于碰撞恢复系数的定义尚未统一，而常见的定义有三种：①牛顿定义法：碰撞恢复系数为碰撞后与碰撞前物体的速度之比；②冲量定义法：碰撞恢复阶段与压缩阶段的冲量之比；③能量定义法：碰撞恢复阶段与碰撞压缩阶段所释放及吸收的弹性应变能之比。本文中碰地和碰壁过程均采用牛顿定义法，及碰撞前后的速度比。根据碰撞过程假设不同，碰撞问题的解决办法有三种：连续接触力法、冲量动量法、基于连续介质力学的有限元法[13]。本文采用冲量动量法确定恢复系数[14]。

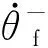
(9)

依据角动量的柯尼希定理，碰撞前的角动量为刚体块对质心的角动量和刚体质心对O′的角动量之和。故碰撞前角动量为

(10)

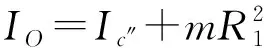
(11)

根据碰撞前后角动量相等可得偏心单刚体绕O′点的碰撞恢复系数

(12)

同理可得偏心单刚体碰地后绕O点(即碰地时偏心单刚体的O点撞击地面)的碰撞恢复系数

(13)

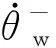
(14)

碰壁前角动量为

(15)

根据碰撞前后角动量相等可得偏心单刚体碰壁时的碰撞恢复系数

(16)

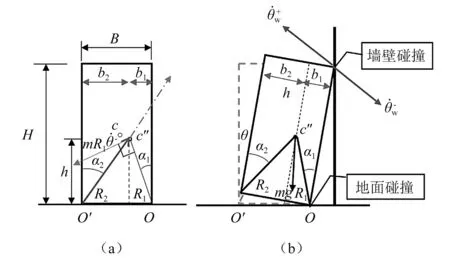
图3 碰撞前后角动量守恒Fig.3 Conservation of angular momentum before and after collision

4 偏心单刚体摇摆响应数值分析

4.1 摇摆运动方程的求解

Rosenbrock积分方法是在隐式Runge-Kutta算法的基础之上，通过采用内嵌牛顿迭代的方式进行显式化，因此也被称为线性隐式积分方法[15]。该方法既保留了Runge-Kutta算法的稳定性，又避免了迭代，提高了计算效率。

根据本文精度和稳定性要求，采用具有二阶精度的Rosenbrock积分方法L-Stable Real-Time compatible algorithm(LRST2)算法。二阶方程不便直接利用Rosenbrock的LRST2方法进行求解，为满足积分方法的要求，需要对原运动方程进行降阶处理。

以式(5)绕O点运动方程为例，进行运动方程的降阶处理，首先把运动方程式(5)转化为

(17)

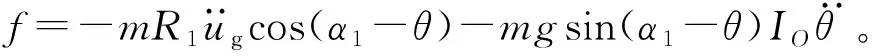
(18)

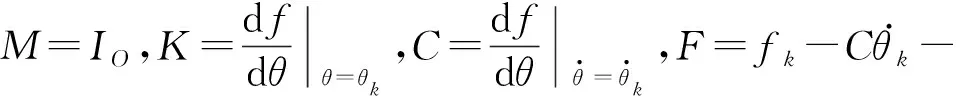
Kθk。

利用Jacobian矩阵对方程进行降阶预处理得到最终表达式为

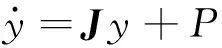
(19)

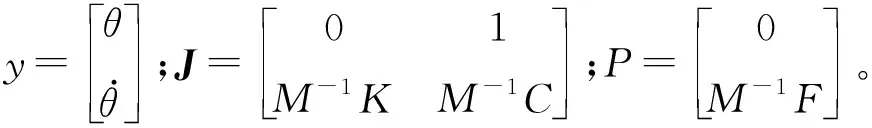
采用Rosenbrock方法时，将地震动时程曲线总时间T等分为N个相等的时间步Δt，即Δt=T/N。令tk=kΔt，则yk表示在tk时刻的状态变量值。应用Rosenbrock方法计算在tk+1时刻的状态变量值yk+1，则

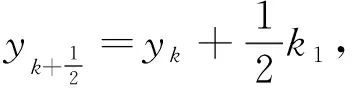
(20)

yk+1=yk+k2,
k2=[I-γΔtJ]-1(Jyk+fk-Jγk1)Δt

(21)

Jacobian矩阵是多元方程组的一阶偏导数以一定方式排列而成的矩阵，体现了一个可微分方程与给出点的最优线性逼近[16]，因此，Jacobian矩阵类似于多元函数的导数。在进行积分计算的时候，只需要在每一步更新Jacobian矩阵，这样就避免了大量的迭代过程，简化了计算。偏心单刚体其他模式的摇摆运动方程都可通过此方法进行降阶预处理，最后将处理后的运动方程采用Rosenbrock数值积分方法进行求解。

4.2 子步-两步法

碰撞前后速度发生变化，碰地时刻还存在运动方程的改变。因此为了准确进行摇摆运动方程求解，需要通过摇摆角来确定偏心单刚体的运动模式。现假定碰壁为正向碰壁，即到正向摇摆角超过某一数值时，刚体与墙壁发生碰撞。

将Rosenbrock积分方法用于本文偏心单刚体摇摆运动响应的问题之中，可以直接对各种模式处理后的状态方程进行求解。为了提高碰撞点的判别精度，本文提出了“子步-两步法”。其原理为在判断可能发生碰撞的积分步长内，插入一定数量的子步，以更小积分步长进行计算；当再次判别到碰撞点时，再采用“两步法”(积分步示意图如图4所示)。下面以偏心单刚体与地面碰撞为例，介绍其计算过程(如图5所示)。假设在点A～点B之间发生了碰撞(摇摆角符号发生改变)，在这个时间段内插入一定数量的子步(示意图中只插入了四个子步)。在以子步步长计算的过程中假设在点C和点D之间发生了摇摆角符号改变，此时假定点C和点D之间摇摆角线性变化，可得到理想碰撞点E。两步中第一步的积分步长为ωt，第二步的积分步长δt-ωt。在C点和D点之间采用“两步法”(如图6所示)，更加准确地识别碰撞点。

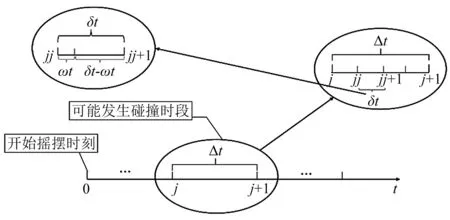
图4 子步-两步法积分示意图Fig.4 Sub-step-two-step integration diagram

图5 子步1两步法Fig.5 Sub-step-two-step method

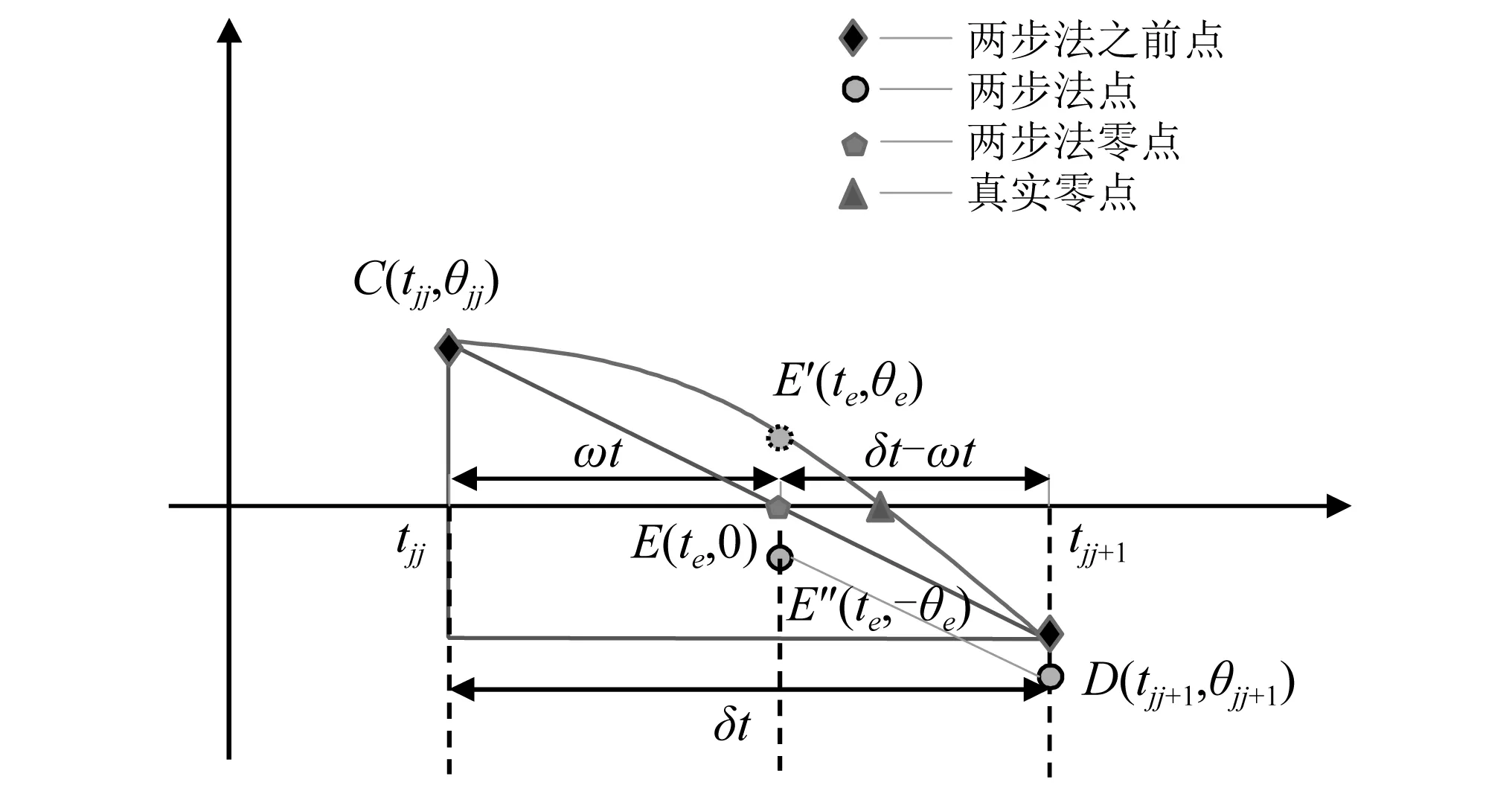
图6 两步法Fig.6 Two-step method

4.3 计算程序与正确性验证

为验证计算程序的正确性，本文的计算模型选取的是文献[17]的模型。该文献中采用的刚体块模型高4 m，宽2 m，质量为124.8 t，碰撞恢复系数取为0.8。地面激励采用1976发生在意大利的Friuli地震，加速度峰值为1.0g，时间间隔为0.005 s，前12 s的加速度时程曲线如图7所示。文献采用的求解摇摆运动方程方法为Runge-Kutta积分方法，最大的步长为0.001 s。本小节对同样的模型采用基于Rosenbrock积分方法的“子步-两步法”方法进行计算，考虑到在原文献中积分采用的最大步长为0.001 s，是五分之一的原始地震动时间间隔，所以在“子步-两步法”将子步数ss=5。通过两种方法计算得到的摇摆角时程曲线对比来验证所本文编写的MATLAB程序的正确性，其计算过程循环示意图如图8所示。循环每一步都包含碰地判断和碰壁判断两个判断条件。这两个判断条件互不影响，因为碰地和碰壁不会同时发生。

图7 Friuli地震波加速度时程曲线Fig.7 Acceleration time history curve of Friuli earthquake

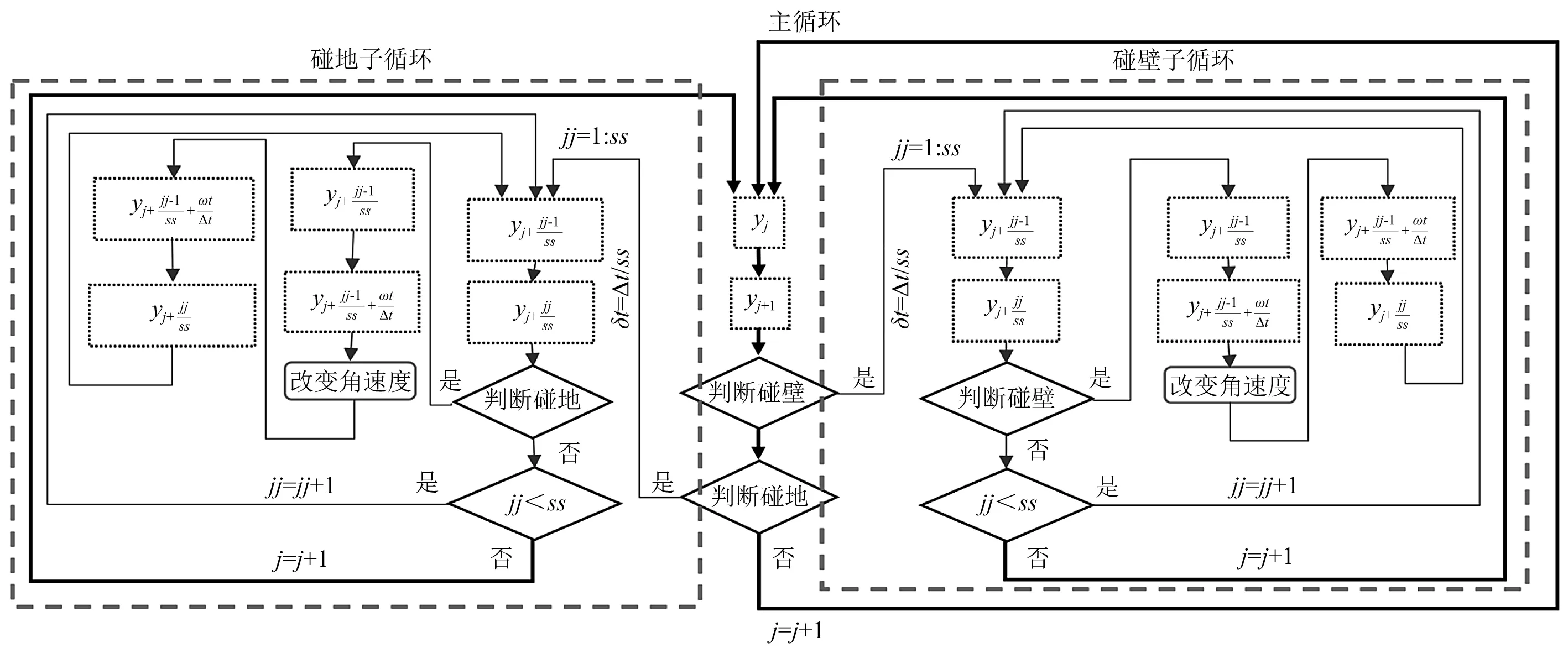
图8 主循环流程图Fig.8 Main loop flow chart

图9显示了参考文献计算结果与本文“子步-两步法”的计算结果。对比“子步-两步”法和参考文献计算结果可以看出，两条曲线吻合度非常高，趋势一致，只在后期存在一些细微差别。由此可知，Rosenbrock积分算法具有较好的精度和稳定性，且“子步-两步法”可以提高计算的精度。

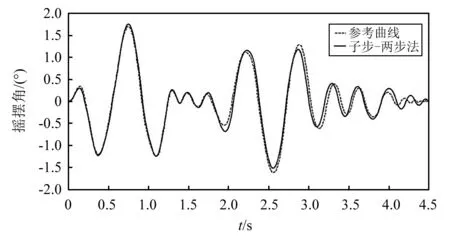
图9 摇摆角计算结果对比Fig.9 Comparison of calculation results

5 理论计算与试验结果对比

试验采用仪器为小型地震振动台系统(WS-Z30-50)和Vic-2D非触式动力响应采集系统。试件参数见表1。

表1 试验试件的参数Tab.1 The parameters of experimental specimens

为了满足碰壁试验的刚度要求，采用两块厚5 mm钢板焊接为L型。用四根20 mm×20 mm(厚2 mm)的铝合金方管组成框架作为墙壁的支撑结构。试验试件设计如图10(其中(a)为正视图，(b)为俯视图)和图11所示。

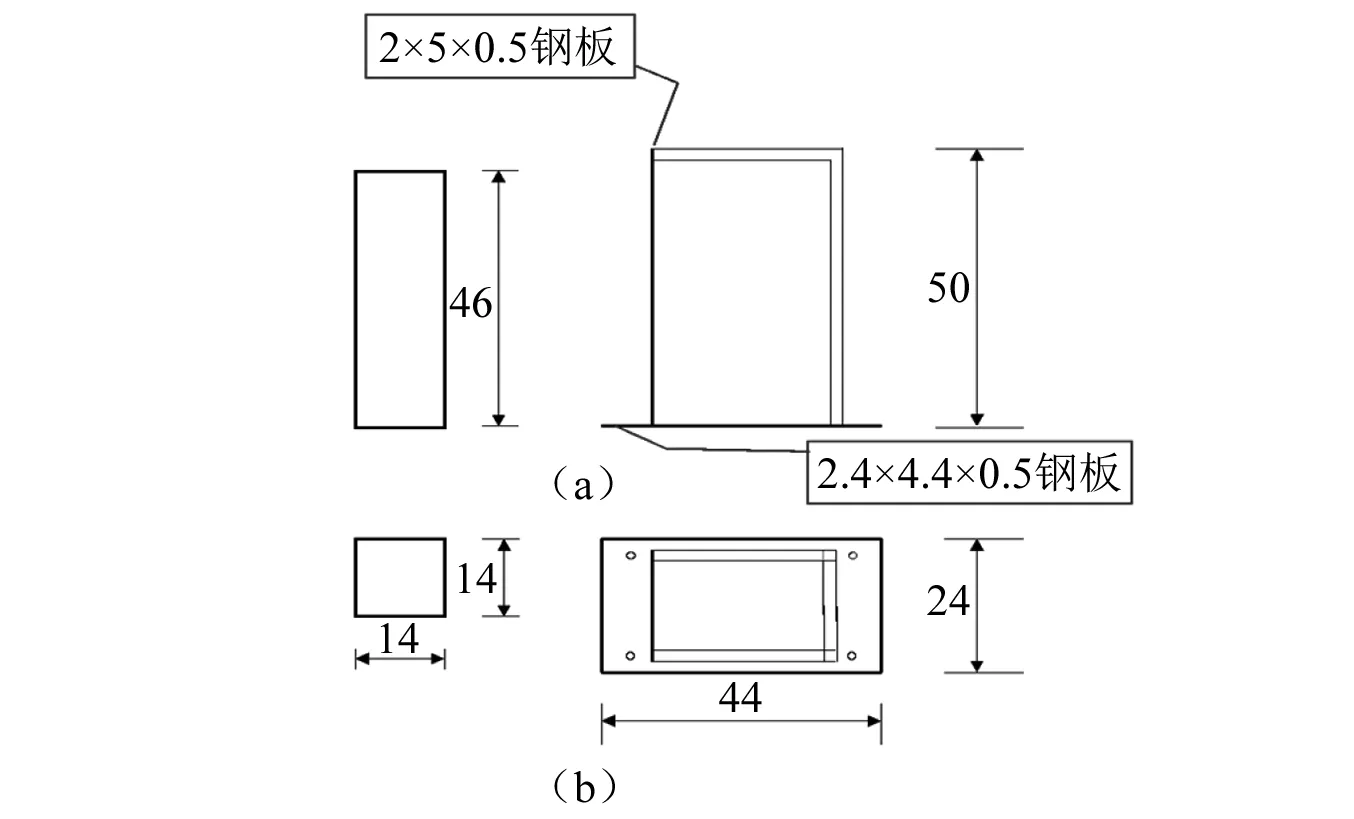
图10 试验试件设计 (cm)Fig.10 Dimension of specimens (cm)

图11 试件配置图Fig.11 The photos of specimens

进行振动台试验前，为方便试验进行，对试验所有的地震动进行命名，采用太平洋地震研究中心强震数据库中的NGA序号命名，如“NGA1493”代表前场效应TCU053EW台站的地震动。通过自由振动试验测得了实际的碰地恢复系数0.901，较理论计算结果0.873偏大。碰壁恢复系数统一取理论推导值1.0。将采用MATLAB编制计算程序，计算结果如图12和图13所示。从图中可以看出无论是在碰壁还是不碰壁的情况下两次试验曲线几乎重合，充分证明了试验试件设计的合理性以及偏心单刚体振动台试验的可重复性。数值模拟结果与试验结果相比，总体走势相近，较试验结果偏大。导致偏差的原因为：数值模拟时假设刚体作单轴向摇摆运动，实际试验过程中不可避免会发生微小的滑移、扭转等现象，导致试验结果较模拟结果偏小。考虑碰壁影响时，碰撞过程更为复杂，不确定性增加，计算结果和试验结果的偏差略大。此外，模拟所得的时程曲线，与试验结果相比，有相位差。这主要是由于刚体与地面接触面不平整，导致试件摇摆运动更早被激发。表2给出了偏心单刚体在地震动作用下试验结果与数值计算结果的摇摆角峰值绝对值的对比结果。本模拟试验结果相比实际结果而言偏大，主要是因为试验中考虑的是最不利的情况下的试验结果。

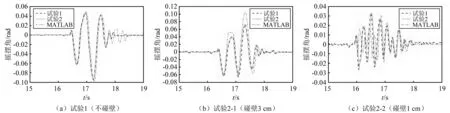
图12 NGA1493地震动作用下单刚体摇摆角时程曲线Fig.12 The rocking angle curve of single rigid block under the NGA1493 wave

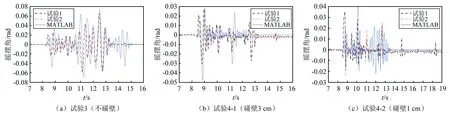
图13 NGA1504地震动作用下单刚体摇摆角时程曲线Fig.13 The rocking angle curve of single rigid block under the NGA1504 wave

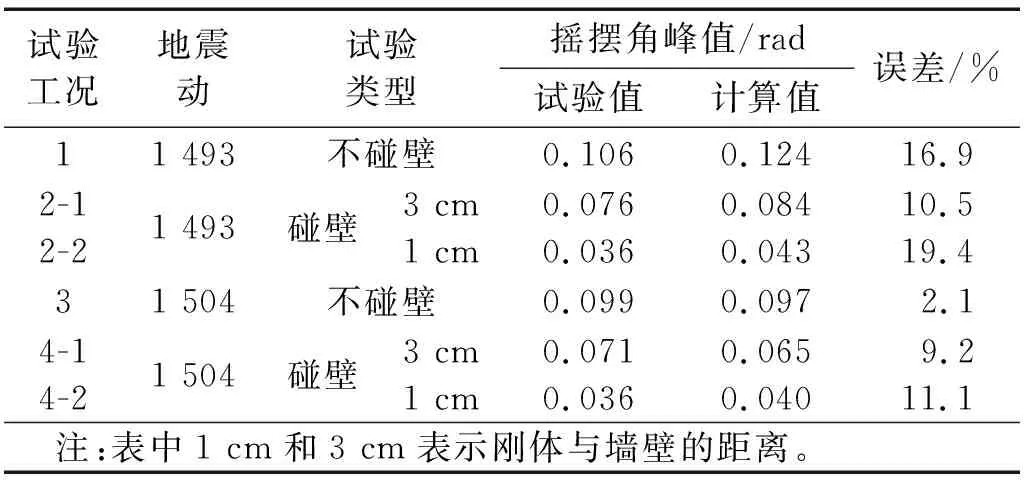
表2 试验结果与计算结果的摇摆角峰值对比Tab.2 The comparison of the peak rotation angle value between the test and the theory

6 偏心单刚体结构摇摆动力响应影响因素分析

为了研究偏心单刚体摇摆动力响应影响因素，参考已有研究选取常用的恒温箱作为计算模型[18]，其尺寸参数见表3。通过设定偏心单刚体块距离墙壁的距离，选定地震动作用NGA1494、NGA1515、NGA1531进行数值模拟，以偏心单刚体结构在地震动作用下的摇摆角峰值为指标来研究碰壁对刚体摇摆响应的影响，计算结果如图14和图15所示。

表3 模型参数Tab.3 Geometric and physical characteristics of the model

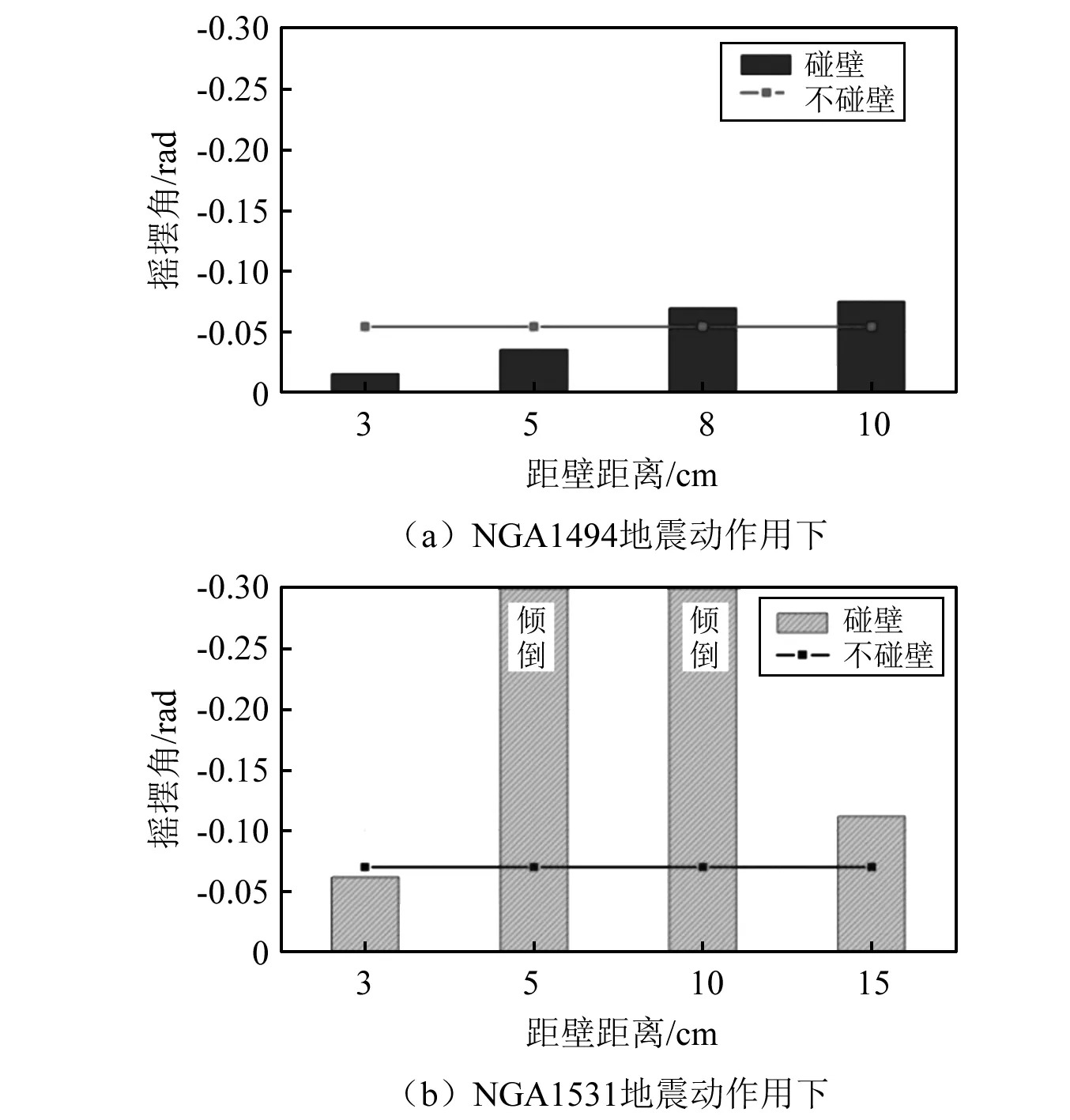
图14 对称刚体碰壁摇摆角与距壁距离的关系Fig.14 The relationship between rocking angle and distance from wall of a symmetric rigid body

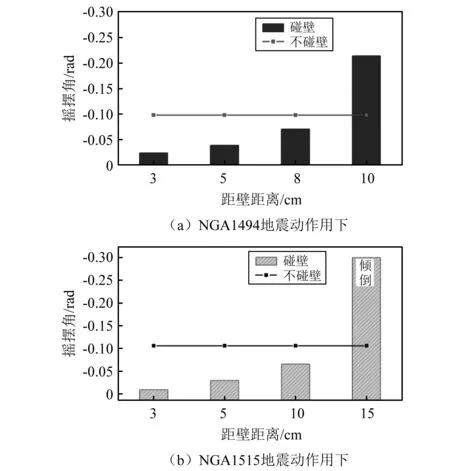
图15 偏心单刚体摇摆角峰值与距壁距离的关系Fig.15 The relationship between rocking angle and distance from wall of an asymmetric rigid body

从图14和图15可以看出，由于碰壁的影响，使摇摆角峰值(绝对值)与无碰壁影响有明显不同，在部分工况下摇摆角峰值明显提高，甚至出现了倾倒现象。这主要是当偏心单刚体正向摇摆碰撞墙壁瞬间，摇摆角速度方向发生变化，会导致地震能量向刚体临空侧积累，从而加剧刚体向临空侧倾倒的危险性。此外，有部分工况摇摆角峰值比不碰壁大幅降低，其原因主要在于碰壁过程伴随着能量损失，使刚体摇摆响应降低。

7 结 论

以考虑侧壁影响的偏心单刚体地震响应为研究对象，通过对偏心单刚体的运动方程推导、动力响应分析及单侧碰壁试验的研究，得出以下主要结论：

(1) 采用Rosenbrock方法建立了偏心单刚体摇摆地震响应分析方法，并提出采用“子步-两步法”将碰撞前后的积分步长进行细分，与试验结果对比发现，该方法具有稳定性强、精度高的优点。

(2) 在有些情况下，考虑刚体块结构碰壁会增加其摇摆响应，增大了倾覆的可能性。因此，研究家具类器物地震影响时，有必要考虑碰壁的不利影响。