智能网联电动汽车经济性巡航速度规划*
张 哲,丁海涛,张袅娜,郭孔辉
(1.吉林大学,汽车仿真与控制国家重点实验室,长春 130022;2.长春工业大学电气与电子工程学院,长春 130012)
前言
目前,全球范围内能源和环境问题日益严峻,人们对汽车工业节能环保的要求也不断提高,而经济性驾驶技术是缓解能源危机和提高汽车燃油效率的重要方法。目前,单车经济性驾驶技术已经逐步成熟。而近年来,智能网联环境飞速发展也给车辆的经济性驾驶带来新的机遇,利用智能交通数据信息的车联网环境下的经济性驾驶技术已成为研究重点。
在网络环境下车辆经济性驾驶的速度优化过程中,道路坡度会对车辆的经济性产生重要影响。车辆在上坡阶段,需要更多的动力来克服由重力产生的坡度阻力;在下坡阶段,重力势能转化为动能,可以有效降低能量消耗。而频繁的加速与制动会造成燃油消耗的增加,研究表明,相比平坦的道路,在丘陵地区车辆的燃油消耗大约要高出5%~20%。因此,基于智能网联信息,利用上下坡度的影响,通过优化本车的驾驶行为,能有效提高车辆的经济性。
在现有研究中,基于规则类的优化、瞬时优化等方法已逐步应用于经济性巡航控制中,Li等基于切换逻辑设计了一种加速−滑行控制策略,在均匀流量和自然流量下与基于线性二次型的基准控制器相比,该控制器的燃油经济性提高20%。Saerens等基于庞特里亚金最大值原理,提出了一种计算汽车在固定坡道上最低油耗驱动控制方法,有效降低了能量消耗。但上述方法主要依靠当前道路信息和已有的驾驶经验作为输入求解控制问题,并未全面考虑动态的交通变化,从而导致控制系统的泛化能力低,很难实际应用。随着优化算法研究的深入,Zhuang等提出了一种基于能量导向的分层递阶电动汽车巡航控制策略,以实现在不同坡度公路上的经济驾驶,同时提高电池寿命。部分文献利用未来路面地形信息,采用动态规划方法优化柴油车的速度轨迹,在不增加行驶时间的情况下燃料消耗降低约3.5%。动态规划方法能有效计算非线性优化问题的全局最优解,但前提是需要获得整个行驶周期中的所有信息,而外界信息的增加,会导致计算过程中“维数灾难”,在车辆实际运行中很难实现。近些年,因预测控制具有前瞻性与有效处理约束的特点,使其在经济性巡航控制方面获得广泛应用。Vajedi等利用非线性模型预测控制理论设计生态自适应巡航控制器来提高丰田Prius的燃油经济性和安全性,仿真结果显示,能源利用率提高约19%。Bakibillah等提出了一种基于模糊规则调整权重的预测控制策略,与传统的人工驾驶系统相比,在相同驾驶时间内可以显著降低燃油消耗与CO等有害气体的排放。Guo等针对时空迁移变化尺度不同的问题,提出基于预测控制的分层控制方法,结合燃料最优速度轨迹和混合动力汽车力矩分配管理来降低混合动力汽车油耗。但智能交通信息的不断融入,导致数据维度不断扩大,预测控制等方法在求解过程中仍然存在计算复杂、优化速度慢的问题,影响系统的实时性,工程应用能力低。
本文针对丘陵道路上电动汽车经济性巡航车速优化问题,综合考虑坡道、限速和前车等外界时变信息,采用分段距离域的方法,构建车速与前方道路信息的映射关系,在预测加优化的框架下,设计滚动距离域的自适应动态规划方法,该方法将滚动优化与自适应动态规划相结合,有效降低控制优化问题的计算维度,并权衡计算效率与控制优化效果,在满足行驶需求的前提下,有效提高车辆自适应巡航的经济性。
1 丘陵道路经济性巡航
在丘陵道路上,基于车载传感器等信息的生态驾驶技术的巡航控制如图1所示,其中道路坡度和周围车辆信息根据车联网系统的V2I(vehicle−to−infrastructure)、V2V(vehicle−to−vehicle)等设备不断更新,主车将接收的环境信息与车辆动力学相结合,在满足车辆自身安全约束的条件下,合理规划巡航车速,并输出适当的需求转矩,使车辆安全、低能耗地完成驾驶意图。

图1 丘陵道路下经济性巡航控制
1.1 车辆运动学模型
以四轮轮毂驱动电动汽车作为研究对象,只考虑纵向动力学控制;驱动力由四轮轮毂电机提供,则电动汽车驱动力表示为

式中:T(=1,2,3,4)为各车轮的驱动力矩;为车轮半径。电动汽车行驶过程中满足如下运动学方程:

式中:为车辆的质量;为旋转质量系数;为车辆加速度;为行驶阻力,包括空气阻力、滚动阻力和坡度阻力。

式中:为阻力系数;为迎风面积;为车辆纵向速度;为重力加速度;为坡度角;为滚动阻力系数。可以表示为速度的函数,式中的单位为km/h。
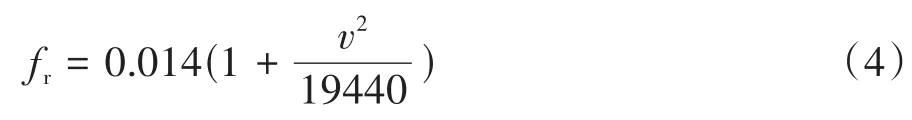
纯电动车在行驶过程中能量消耗以电池消耗电量表示:

式中:为消耗功率;为运行时间;为总需求力矩;η为电机效率。当=1时,电机转矩为正,消耗电池能量;当=−1电机转矩为负,进行能量回收。
本文中动力源为Protean Electric PD16电机,驱、制动电机效率特性如图2所示。本文只考虑车辆纵向运动,驱动力采用左右平均分配,前后力矩按载荷分配。该方法是根据坡道上的载荷转移调整前后力矩比例系数,能有效保证车辆的稳定性,前后轴制动力采用文献[20]中提出的再生制动策略,左右平均分配,其不足部分由液压制动补足。
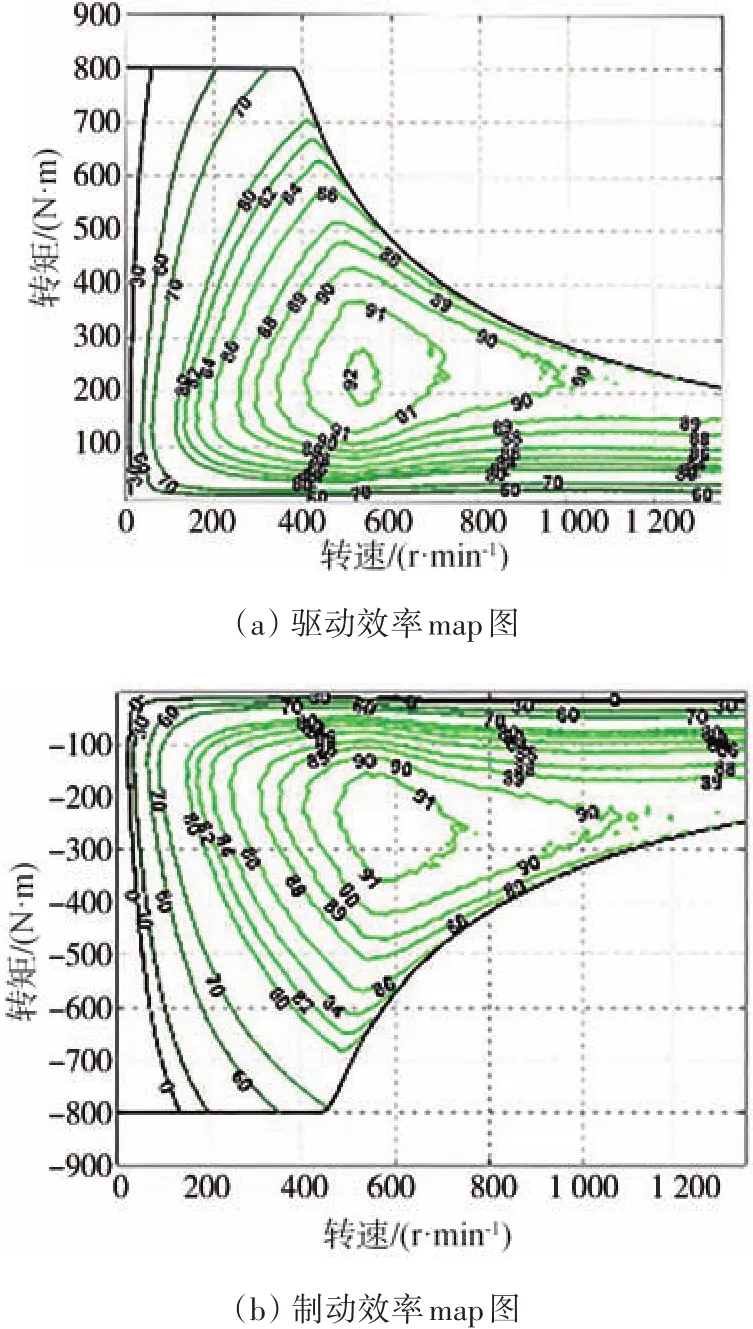
图2 电机效率map图
1.2 面向节能的速度规划问题构建
对于智能网联环境下的车辆,基于距离的道路信息更容易获得,为了建立车速与行驶距离的映射关系,对控制优化问题进行距离域离散:定义优化的总距离为,离散的每个距离域长度为Δ,即全程的优化总步数=/Δ,结果上取整。设定下标表示滚动优化阶段,即每次滚动优化总步数表示为N,为了节约计算资源,本文根据高精地图获得的前方坡度值设计优化步数,表示为

式中:为当前位置到前方路段最近的海拔最高点的距离;为当前位置到前方路段最近的海拔最低点的距离。
设定当前步状态为,控制系统状态量为速度和运行时间,即=[,]=[,],控制输入为车辆加速度:=[]。在第次优化过程中,优化问题表示如下:

性能指标中:第1项为能量消耗,由式(5)计算得到;第2项为系统控制输入的幅值约束,防止过大的加速度导致舒适度下降;第3项表示通行效率,使车辆在ACC设定车速附近波动,防止车速过慢,影响其他车辆通行;第4项为跟车安全距离约束,防止发生碰撞。
本文中将本车不触发AEB的安全制动距离表示为前后车安全距离,本车制动距离表示为

式中:为最大制动减速度,取值0.4 m/s;为系统反应时间,取值0.2 s。前车制动距离=(1/2);最小安全距离=−;两车之间的距离Δ=(−1)+(−1) Δ()−[(−1)+Δ]。与前车的安全距离作为惩罚项:本文中选择sigmoid函数作为惩罚项,即Δ−值越大,惩罚越小,反之惩罚越大。
2 基于滚动距离域近似动态规划方法的速度规划
为了实时获得经济性巡航的优化车速,即求解1.2节中速度规划问题的最优解,本文提出一种滚动距离域近似动态规划方法对巡航控制系统的加速度进行求解,该方法是一种在线优化控制方法。基本思想是将优化问题离散,在每个预测域内采用近似动态规划求解一个最优控制序列,并将优化序列的(≤N)个控制量作用到系统中,并进行滚动,进行下一次优化。算法结构如图3所示。

图3 滚动时域近似动态规划算法结构图
2.1 回报函数
回报函数()是学习算法的重要指标参数,在本文中为速度规划问题的目标函数即式(7)第1式,单步回报函数表示为
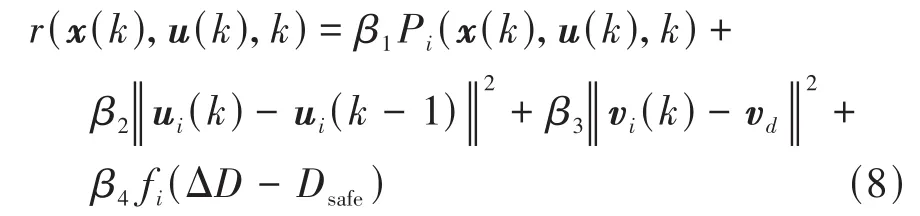
系统回报函数表示为

2.2 动作网络


图4 动作网络结构图



权值()修正迭代公式表示为

式中为动作网络学习率,它一般会随时间的增加而逐渐减小至一个较小的固定值。
2.3 评价网络
评价网络用于近似代价函数(),评价网络的输出表示为


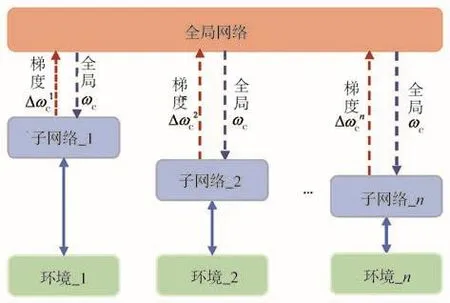
图5 评价网络异步更新结构图


根据Bellman最优值原理,最优值函数表示为

最优控制表示为

2.4 时序差分(temporal-difference,TD)误差函数
TD误差函数用来修正评价权值,根据式(15)累积代价误差表示为
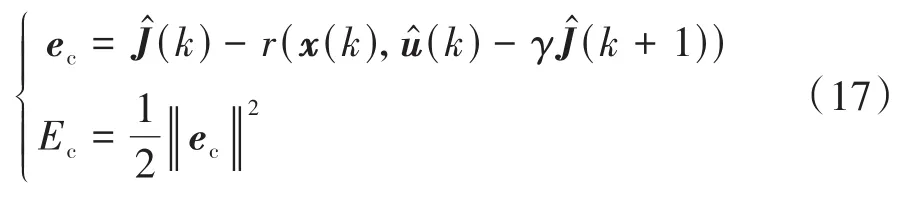
评价网络误差()更新规则如下:

式中()为评价网络学习率,与动作网络学习率相同,一般会随时间的增加而逐渐减小至一个较小的固定值。滚动距离域近似动态规划原理图如图6所示。
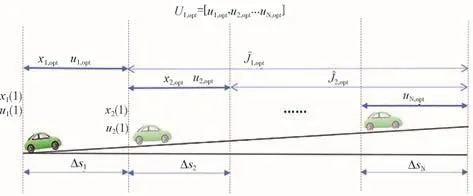
图6 滚动距离域近似动态规划原理图
在每个预测域内,采用近似动态规划方法求解有约束的最优控制问题,算法流程如表1所示。

表1 优化流程表
3 仿真结果与分析
为了实现和验证所提出的控制算法适用于不同山地道路交通场景,采用设计的仿真路段与真实路段信息两种情况进行仿真分析,以评价本文提出的经济性巡航方法。智能网联汽车硬件在环仿真平台包括驾驶模拟器、运行控制算法dSPACE、运行实时车辆模型的目标机、SCANeR交通场景模型的主机和运行Carsim车辆模型与控制主机5部分组成,硬件在环仿真平台如图7所示。驾驶员在驾驶模拟器中操纵转向盘,速度规划模块根据以太网传输的实时路况信息和车辆状态计算需求力矩,将转向盘信息与需求力矩信号同时发送到目标机,计算得到车辆的位置与状态变化,并通过以太网发送到交通场景和速度规划模块,驾驶员和规划模块根据位置场景变化同时控制车辆。

图7 智能网联汽车硬件在环仿真平台
本文所用车辆参数如表2所示。电动汽车的初始速度设置为60 km/h。仿真的电脑配置为Intel(R)Core(TM)i7−6700 CPU。

表2 车辆参数
仿真中,每个时域内的最大迭代次数设定为=50。离散系统的距离Δ=5 m,网络迭代误差如图8(a)和图8(b)所示,代价函数收敛曲线如图8(c)所示。
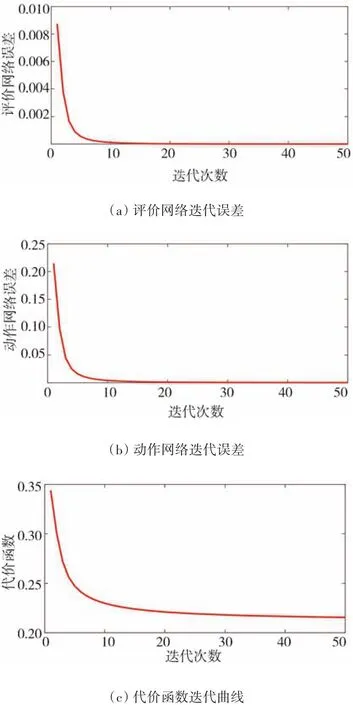
图8 网络迭代误差及代价函数曲线
3.1 单坡道场景
按照道路设计标准,本文中选择的典型单坡度场景如图9所示。
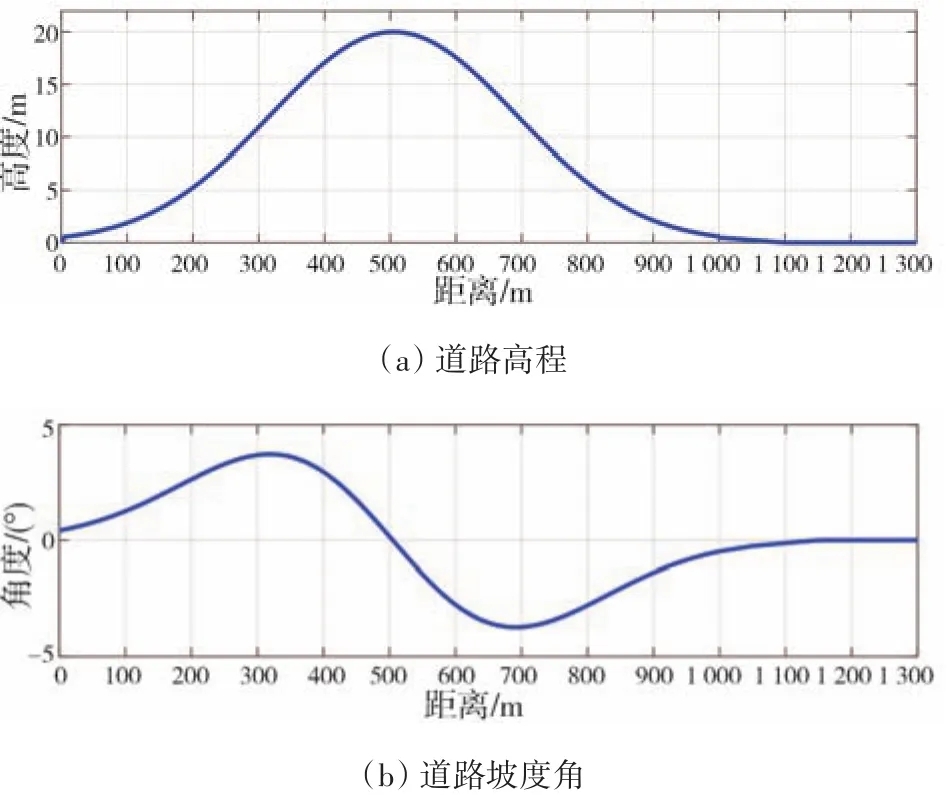
图9 单坡道场景信息
在1.3 km的仿真路段上,采用自适应巡航控制(ACC)和本文所提方法规划车辆的行驶速度,仿真结果对比如图10所示。
车辆在上坡阶段,需要提供更多的动力来克服由重力因素产生的坡度阻力;在下坡阶段,重力势能转化为动能,可以有效降低能量消耗。由图10可知:经济性驾驶车辆在进入上坡阶段适当放宽速度容许范围并按照预先计划的方式缓慢增加车速,预计车辆能平稳通过上坡后,适当降低车速;在下坡阶段,有效利用自身的重力势能,允许速度在容许范围内增加,将重力势能有效转化为动能。在经济性方面,能量消耗对比如图10(d)所示,与ACC定速巡航相比,能耗降低约5.91%。

图10 典型单坡度场景对比图
3.2 多坡道场景
为了验证优化控制器的有效性,选择一段真实丘陵道路,长约3 km,道路坡道信息如图11所示。首先根据坡度值确定优化长度,例如,0−450 m为一个优化长度,并根据设定的距离域长度进行分段。

图11 丘陵道路场景信息
与上一节相同,采用自适应巡航控制(ACC)及本文所提方法控制规划车辆的行驶速度,仿真结果对比如图12所示。
由图12(a)速度图对比可知,经济性驾驶策略的速度会根据前方坡度参数对行驶速度在容许范围内进行调整。例如在0.6−1 km之间,经济性行驶方法在预测车辆可以平稳通过坡度最高点后,适当放宽车速容许范围,采用自身原有动力克服坡度阻力,达到降低能耗的目的;在1.9−2.2 km之间,利用下坡重力势能优势,尽可能将重力势能转化为车辆的动能,适当增加车速,减少车辆因制动力矩过大造成的能量耗散。在经济性方面,能量消耗对比如图12(d)所示,与ACC定速巡航相比,能耗降低约10.39%。以某品牌电动汽车为例,电池满电量平均约为50 kW·h,在同等转化效率的条件下(即不考虑气温、空调及其他因素),续航里程提高约9.5%。
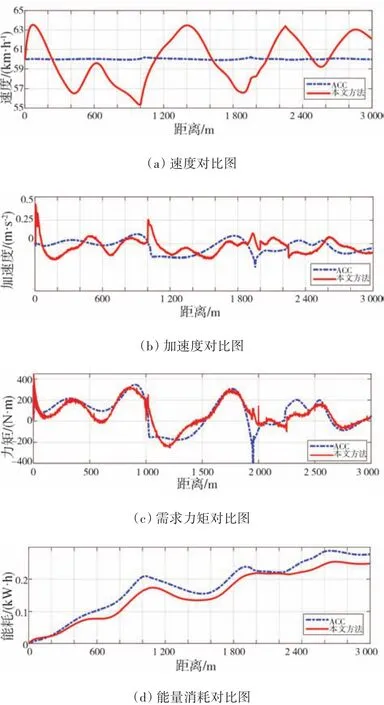
图12 多坡道路场景对比图
车辆仿真中,两种方法在3 km路面的运行时间如表3所示,可以看出,运行时间基本相同,本文提出的方法在不损失通行时间的基础上具有显著的节能效果。

表3 通行时间
4 结论
本文基于智能交通系统,提出了一种基于滚动距离域近似动态规划的经济性巡航速度规划方法。该方法采用距离分段,有效解决了行驶速度与空间道路信息两者难映射的问题;并提出滚动距离域近似动态规划方法,能够快速求解车辆在多坡道地形上经济性行驶的巡航车速,在保证通行效率的基础上,减少智能交通环境下的能源消耗,该方法计算维度低,具有工程应用能力。并通过搭建智能网联汽车硬件在环仿真平台对控制策略进行验证,与自适应巡航相比,在不增加通行时间的基础上,能源消耗降低约10.39%,续航里程提高约9.5%。

