含局域共振单元复合材料格栅夹芯结构的吸声性能研究
罗英勤, 楼京俊, 张焱冰
(海军工程大学 舰船与海洋学院,武汉 430000)
随着传统吸声结构越来越难满足水下结构物低频隐身需求[1-5],具有超常物理特性的局域共振声学超材料逐渐被应用到低频吸声控制领域。Liu等[6]首次提出了局域共振声子晶体,其低频带隙处声波波长大于散射体尺寸两个数量级,为低频声控制开辟了新思路。Zhao等[7-10]在水声吸声材料聚氨酯基体中引入硅胶包覆的金属球作为局域共振散射体,在低频段实现了很高的吸声系数,为覆盖层设计提供了重要技术途径。Zhao等采用多重散射理论对其吸声机理进行分析,表明纵波在局域共振散射体的作用下更容易转化成易耗散能量的横波且吸声峰频率与金属球密度关系密切。Wen等采用多重散射理论和有限元方法进一步对该结构吸声性能进行了分析,建立了周期单元的共振模态和吸声谱之间的关系。Meng等采用遗传算法对两层含有不同球型局域共振散射体的吸声材料进行了优化设计,得到了吸声频带更宽的优化结果并对结果进行了实验验证。吕林梅等采用简化的有限元方法对含有不同形状局域共振散射体吸声结构的声学性能进行了分析。总之,局域共振型吸声结构是控制低频吸声非常有效的结构形式。
对于潜艇隐身,传统吸声覆盖层还面临着静压作用下吸声性能变差的问题。静压能引起吸声结构内部空腔形状或材料动态力学性能发生变化,因此深水环境下结构吸声性能也发生变化[11],但是考虑静压的吸声结构声学性能研究文献并不多。姚熊亮等[12]研究了水深对隔声去耦瓦吸声系数的影响,认为可将黏弹性材料近似为高黏性流体。邹明松等[13]采用传递矩阵法建立了静压下吸声覆盖层的声阻抗求解方法。姜闻文等[14]利用有限元法分析了不同空腔结构吸声性能受静压的影响。陶猛等[15]考虑静压作用推导了吸声覆盖层声学性能计算的传递矩阵法。Panigrahi等[16]采用有限元法计算了静压下不同组合空腔结构的声学性能。张冲等采用有限元讨论了静压对球形空腔吸声覆盖层的影响。这些研究均表明实际应用中,不可忽略静水压力对结构吸声性能的影响。
本文综合考虑低频吸声和耐静压需求,提出了一种含局域共振单元的复合材料格栅夹芯结构。众多研究表明复合材料格栅加筋结构是非常有效的承压结构[17-21]。本文在该格栅结构中引入可实现低频吸声的局域共振微结构,以实现耐静压低频吸声结构设计。结构面板为透声性能良好的高强玻纤,保证结构强度的同时确保声波能够进入结构;夹芯层为格栅加筋以增加结构刚度减小变形;格栅格内填充局域共振型吸声结构。
1 吸声型复合材料格栅夹芯结构模型
含局域共振单元的复合材料格栅夹芯结构模型如图1所示,结构由上下面板和格栅夹芯层构成,面板为高强玻纤,蜂窝格栅骨架为浮力材料,面板和格栅通过胶结剂粘结,格栅内填充内嵌有软橡胶包覆铁球的局域共振散射体单元的聚氨酯基体。设结构在二维平面无限延伸,格栅夹芯呈六边形周期性排列。如图2(a)所示为复合材料格栅夹芯结构的一个周期单元,以单元底面中心为原点建立笛卡尔坐标系;如图2(b)所示为周期单元在y=0处截面示意图,单元高度为H,上下面板厚度为t;如图2(c)所示为周期单元在z=H/2处截面示意图,格栅骨架边长为a,格栅骨架厚度为b,局域共振散射体半径为rc,散射体芯体半径为rx。
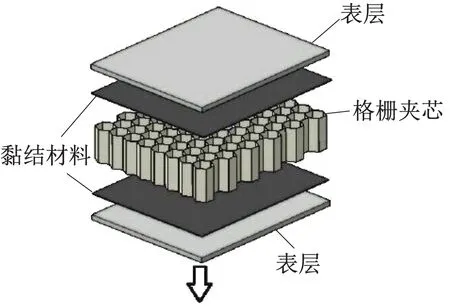
图1 复合材料格栅夹芯结构模型示意图
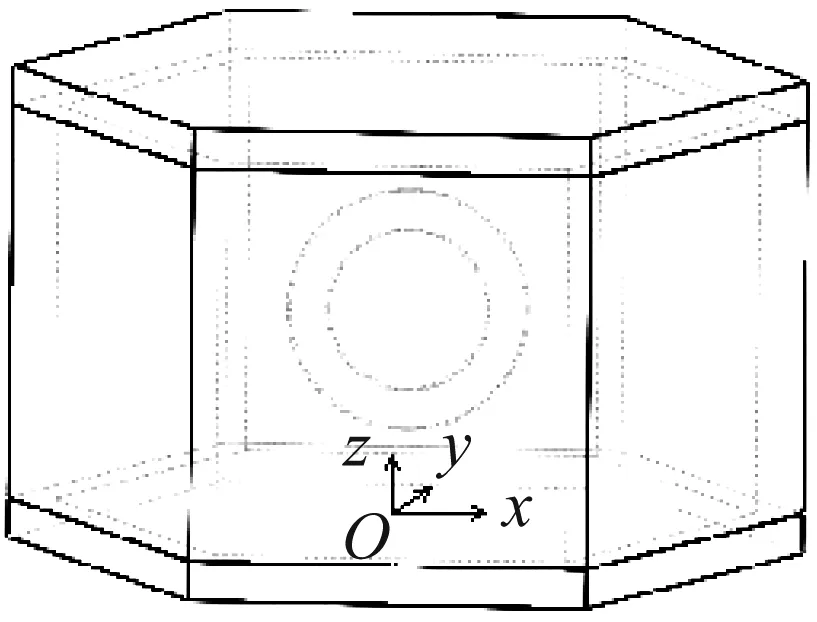
(a)
2 仿真模型
2.1 有限元仿真方法
保证格栅内所填充基体的通孔率相同,将六棱柱周期单元转化成圆柱周期单元,再利用结构的轴对称特性将三维模型简化为二维轴对称模型[22]。采用COMSOL Multiphysics多物理场分析软件建立的二维轴对称仿真模型如图3所示,吸声结构入射端为半无限水介质,一列平面纵波从其中垂直入射至结构表面,吸声结构后端为半无限空气介质。流体介质两端分别施加PML层形成吸声端面以模拟无限介质边界;柱面边界2设置法向位移为0模拟周期性边界条件。仿真模型提取结构反射系数R和透射系数T,由于透射侧为空气,阻抗严格不匹配,透射系数T考虑为0,则吸声系数为α=1-R2。
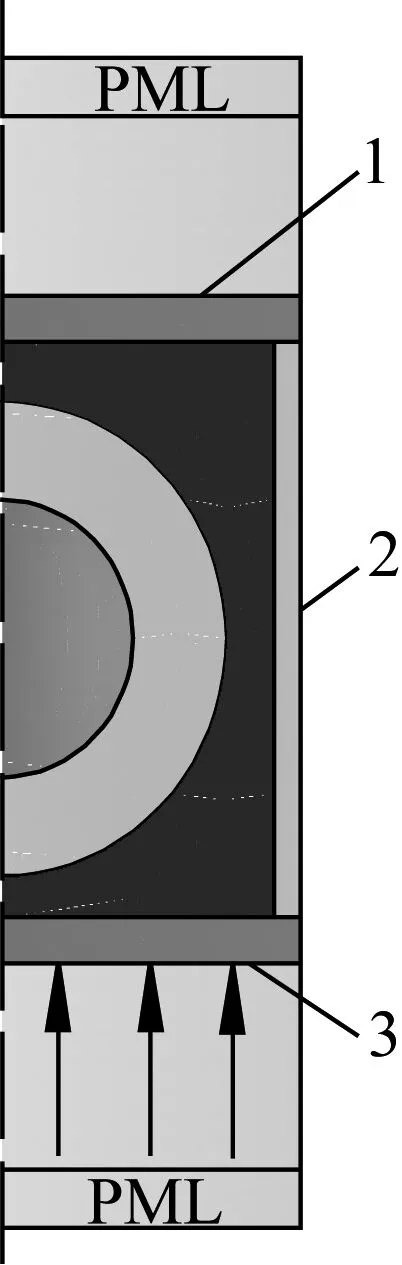
图3 二维轴对称模型示意图
为计算静水压下结构吸声性能,首先计算静水压作用下吸声结构的变形,再对变形后的结构重新划分网格计算其吸声性能。计算过程忽略结构变形产生的残余应力。如图3所示,结构变形计算中,将边界1固定,在边界3施加静水压力,其他边界条件保持不变。
对比文献[7]局域共振结构吸声性能的理论及实验值,对本文方法进行验证。如图4所示,模型为二维周期性结构,晶格参数为s=19.5,样件直径D=118 mm,厚度为h=L1+L2+L3=55 mm,其中L1=L3=13.75 mm,L2=27.5 mm,局域共振散射体芯体半径rx=5 mm,包覆层外径rc=7.5 mm。文献[7]为保证实验结果的可靠性,制备了2组模型,标号分别为2和R2,计算结果如图5所示,实验值与理论值的吸声峰幅值及频率分别吻合较好,且本文方法计算结果与文献理论解吻合一致,验证了本文方法的有效性。实验测试值与理论解之间的误差原因可能有:实际实验样件中有不可避免的小气泡,气泡的存在会增加声散射,影响吸声系数;实际样件中散射体位置具有随机性;实验中结构局域共振作用对材料动态黏性属性有影响。另外,理论解对无限大周期平板结构进行计算,而实验样件仅能对有限个周期单元进行测试,边界条件也会对吸声系数产生一定影响。
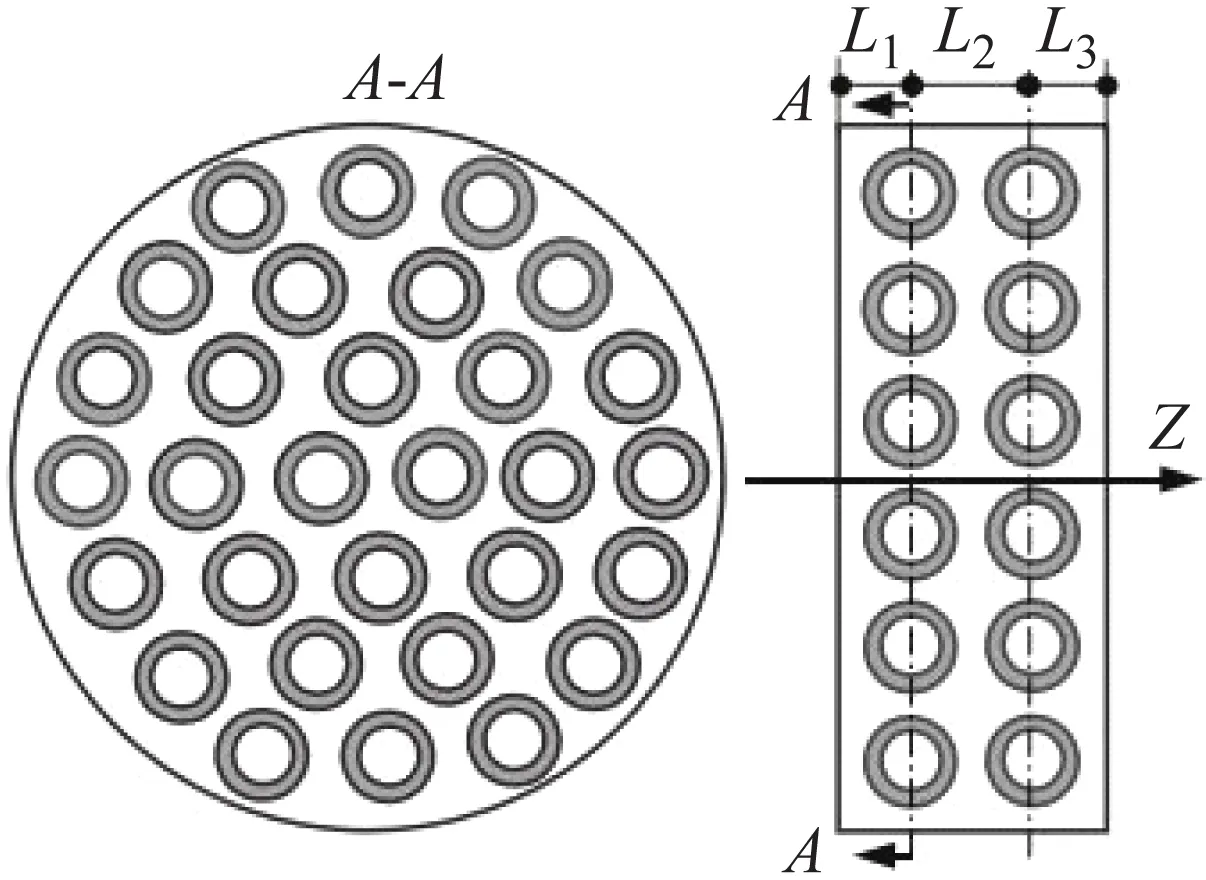
图4 文献[7]局域共振模型示意图
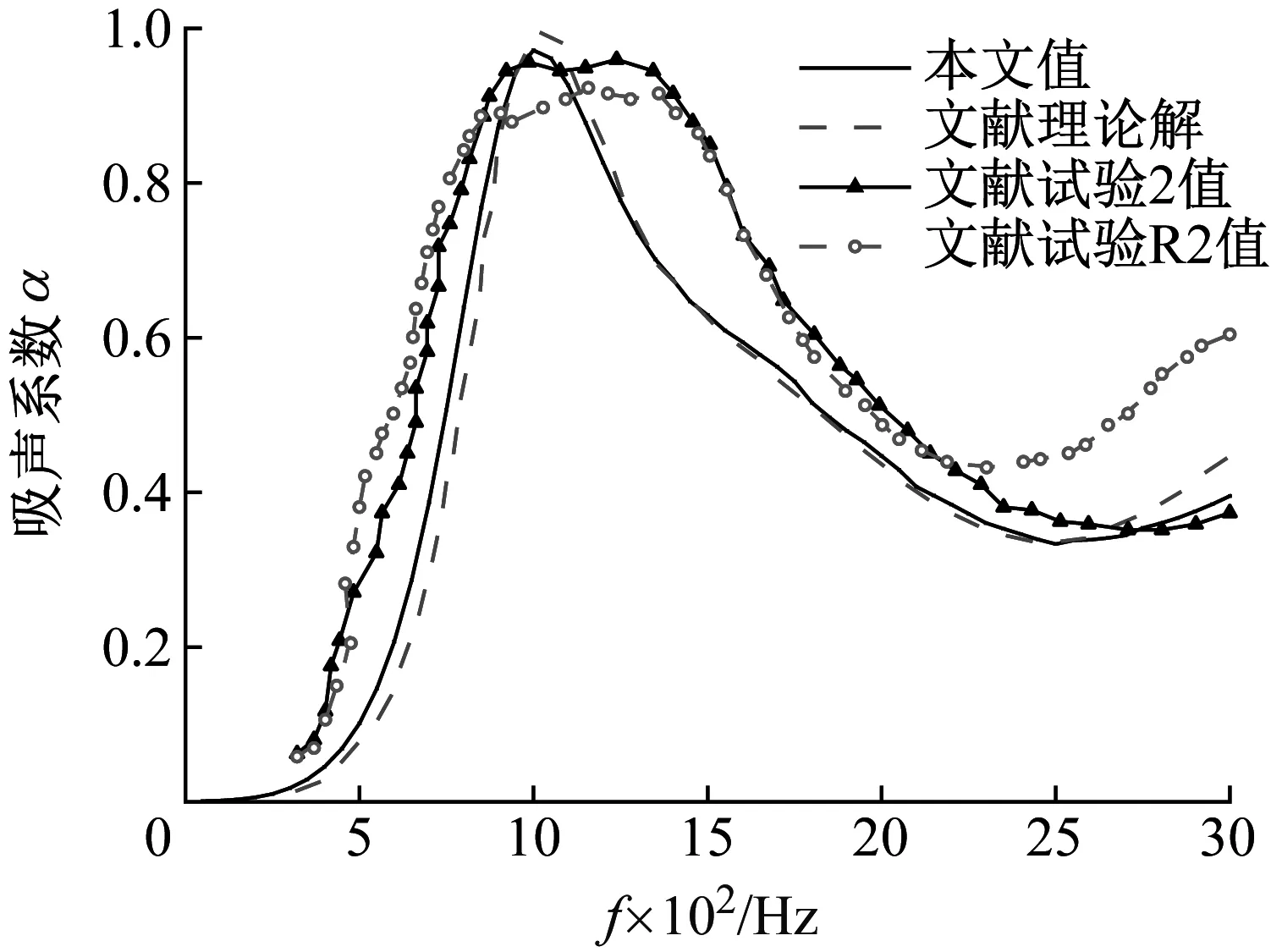
图5 文献[7]局域共振模型吸声性能验证结果
2.2 能耗功率密度场
结构吸声性能一方面和表面阻抗与流体特性阻抗的匹配程度有关,另一方面与结构内声能耗散机理有关,因此声能耗散功率密度场对研究吸声机理有重要意义。吸声结构往往由含有阻尼特性的黏弹性材料组成,由粘弹性介质中能量守恒关系可知,介质中某区域V的边界受到外部作用做功的时间平均功率,与V内部的时间平均耗散功率〈Pab〉相等[23]
(1)
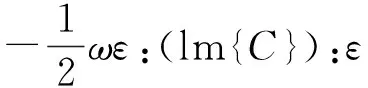
3 复合材料格栅夹芯结构吸声性能分析
模型几何参数如表1所示。结构面板为各向异性复合材料,杨氏模量为E1=E2=18 GPa,E3=5 GPa,泊松比为v12=0.16,v23=v13=0.3,密度为ρ=1 800 kg/m3,损耗因子忽略不计。其他材料参数如表2所示。研究频段为2 000~5 000 Hz,步长取为50 Hz。建模过程最大网格尺寸设为3 mm,远远满足1/4最小波长网格大小的精度要求[24]。分别计算常压和3 MPa下的吸声系数。

表1 模型几何参数
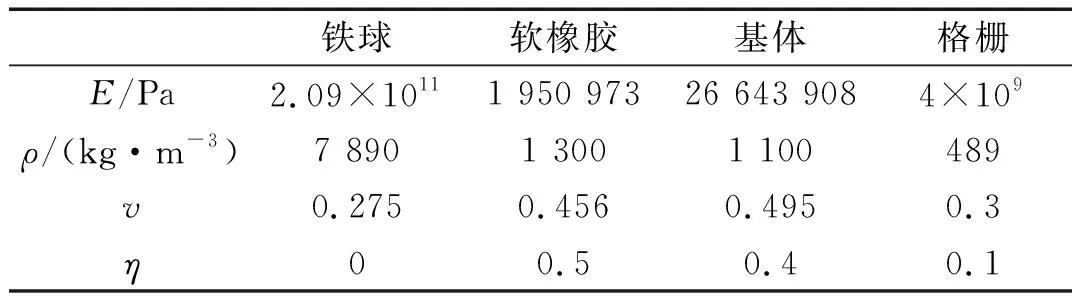
表2 模型材料参数
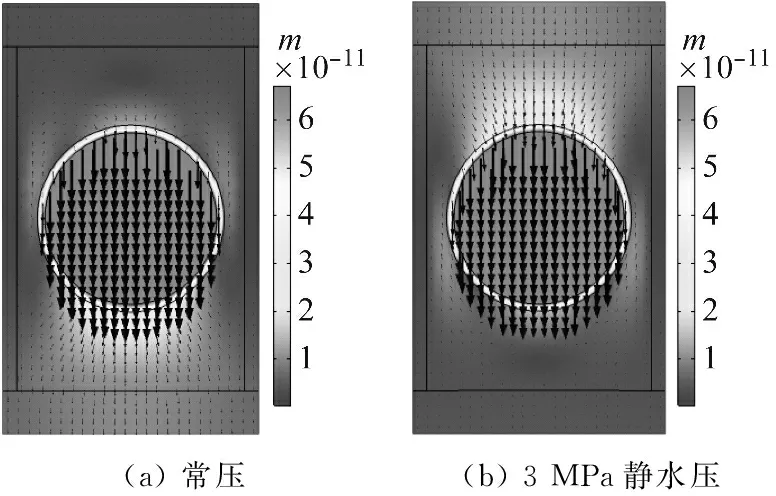
计算结果如图6所示,常压和3 MPa静水压作用下吸声系数非常接近,研究频段内的平均吸声系数分别为0.306和0.309,平均相差1.13%,两者几乎相等,说明本结构吸声性能在静水压作用下稳定性良好。研究频段内常压和3 MPa静水压作用下吸声系数曲线分别在2 150 Hz和2 200 Hz处形成了吸声系数峰值,图7和图8分别给出了该频率处常压和3 MPa静水压作用下结构中面的位移分布图和能量耗散密度分布图,位移分布图中箭头表示质点位移矢量,箭头方向表示位移方向,箭头大小表示位移相对大小。由图可知,常压和静水压作用下的位移分布图和能耗功率密度曲线分布图分别几乎相同,进一步说明吸声结构的吸声性能在静水压作用下的稳定性良好。另外,从位移分布图可以看到吸声系数波峰处几乎是铁球作纵向运动,从能量耗散密度分布图可知声能主要在软橡胶包覆层耗散。图6给出了常压和3 MPa静水压作用下包覆层的能量耗散值,平均能耗曲线趋势几乎与对应吸声系数一致,且分别在2 150 Hz和2 200 Hz处形成平均能耗曲线波峰,均与吸声系数峰值频率位置对应。表明波峰由铁球纵向共振引起,铁球运动带动包覆层发生剪切变形,其剪切应变分布如图9所示。剪切变形更易促进纵波模式向横波转化并耗散声能,最终声能主要在包覆层耗散。
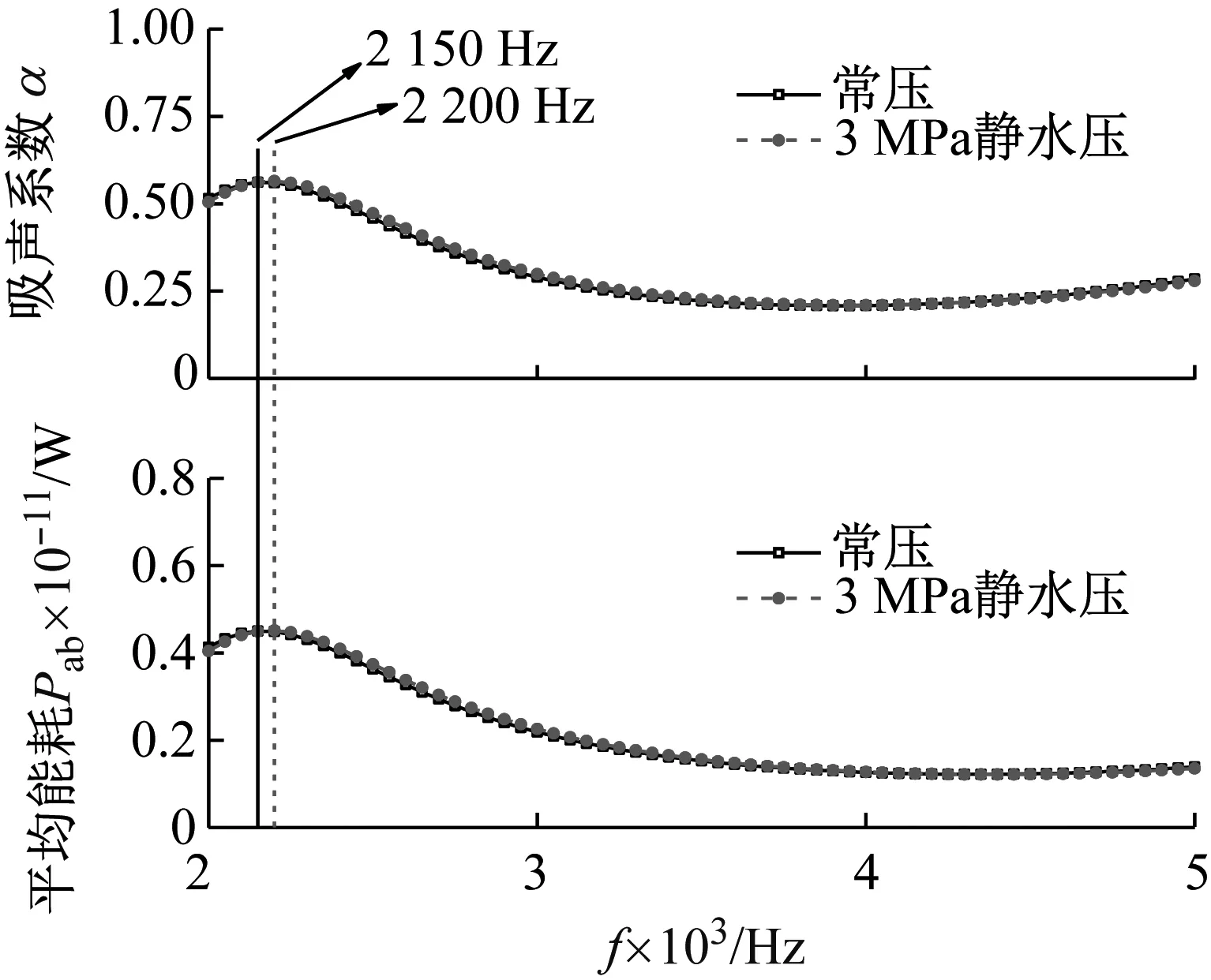
图6 吸声系数与平均能耗曲线对比图
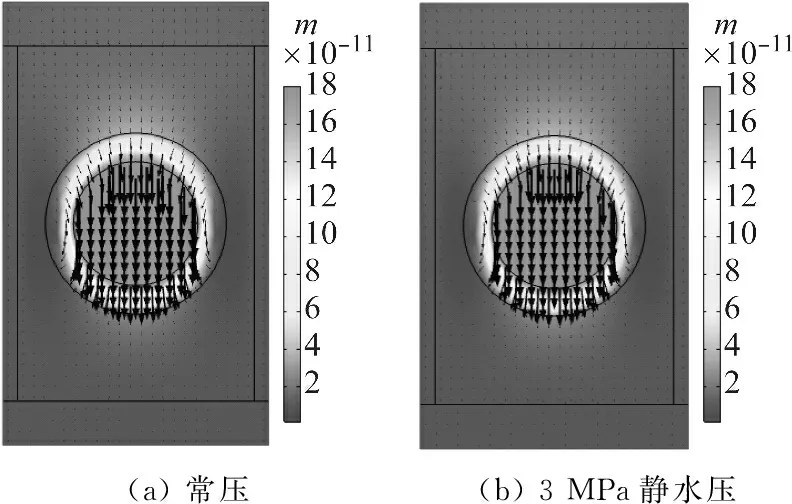
图7 吸声系数曲线波峰处位移分布图

图8 吸声系数曲线波峰处能量耗散密度分布图

图9 吸声系数曲线波峰处剪切应变分布图
4 复合材料格栅夹芯结构吸声性能优化设计
采用MATLAB的遗传算法GA函数联接有限元仿真软件对常压下结构二维轴对称模型的宽频吸声系数进行优化设计,优化频段为2 000~5 000 Hz,步长取为50 Hz。综合考虑研究频段内最差吸声系数和平均吸声系数的平衡,分别对频段内吸声系数最差值和平均值加权建立适应度函数F下
F(D)=-q(minf∈[f1,f2]α(f;D))-
(2)
式中:D表示设计变量,此处设计变量为a、rc和rx;q为权重系数,此处取0.5,GA函数目标是获取适应度函数最小值。引入几何因子β、γ和ξ对设计参数作无量纲化处理,设六边形周期单元边长a的等效半径为r=(3+10β)mm,rc=2 mm+γ(r-2.5 mm),rx=1 mm+ξ(rc-1.5 mm)。其中β、γ和ξ为无量纲化的优化设计参数,参数范围为[0,1],此时原始设计变量自然满足以下几何关系,保证了优化过程几何建模的鲁棒性。
rc (3) 优化后参数如表3所示,对比优化后模型在常压和3 MPa静水压作用下的吸声系数如图10所示,平均吸声系数分别为0.767 7和0.767 6,相比于优化前平均提高约150%。且常压和3 MPa静水压作用下的吸声系数平均相差0.01%,二者几乎相等,表明在复合材料夹芯结构的格栅芯层填充吸声材料是非常稳定的耐压型吸声结构设计形式。研究频段内常压和3 MPa静水压作用下吸声系数曲线在3 400 Hz和3 500 Hz频率下吸声系数均达到峰值0.99,几乎完美吸声,且此时结构厚度与波长关系为H<λ/14,表明吸声结构采用较小厚度实现了低频吸声控制。图11和图12分别给出了吸声系数峰值频率处常压和3 MPa静水压作用下结构中面的位移分布图和平均能量耗散密度分布图。由图可知,与优化前相似,常压和静水压作用下的位移分布图和能耗功率密度曲线分布图分别几乎相同。另外,从位移分布图可以看到吸声系数波峰处几乎是铁球作纵向运动,从能量耗散密度分布图可知声能主要在软橡胶包覆层耗散。图10给出了常压和3 MPa静水压作用下包覆层的平均能量耗散值,平均能耗曲线趋势几乎与对应吸声系数一致,且分别在3 400 Hz和3 500 Hz处形成能耗曲线波峰,与吸声系数峰值频率位置对应。表明吸声机理与优化前保持一致。 图10 优化后吸声系数与平均能耗曲线对比图 图11 优化后吸声系数曲线波峰处位移分布图 表3 优化后参数值 图12 优化后吸声系数曲线波峰处能量耗散密度分布图 本文提出了一种耐静水压吸声型复合材料格栅夹芯结构模型。结构格栅内填充聚氨酯基体,基体内嵌入软橡胶包覆铁球的局域共振散射体单元。 分别在常压和3 MPa静水压作用下对结构的吸声性能进行对比计算,结果表明,吸声性能在静水压作用下稳定性良好。通过讨论吸声系数、平均能耗曲线、位移场和能耗密度场的关系,对结构吸声机理进行了分析,结果表明研究频段内的吸声系数峰值由填充基体内局域共振单元的铁球发生纵向共振引起,可以通过调整铁球、包覆层和基体的几何尺寸来调整结构的吸声性能。以此为基础,本文采用遗传算法,在常压下对结构在宽频范围的吸声系数进行了优化设计,优化后吸声系数提高约150%,且在低频点3 400 Hz处吸声系数达到0.99,接近完美吸声,且此时结构厚度与波长关系为H<λ/14,表明吸声结构采用较小厚度实现了低频吸声控制。对比优化后结构在常压和3 MPa静水压作用下的吸声性能,结果表明优化前后常压和3 MPa静水压下的平均吸声系数相差均不大于1.2%,进一步证明了结构吸声性能在静水压作用下稳定性良好。 可以考虑在优化模型中引入更多材料参数和几何参数获取更优的吸声性能。另外,通过在多个格栅格内填充多种结构形式的针对不同低频点实现完美吸声的局域共振单元有望实现低频宽带吸声性能设计。因此,本模型为耐静水压下低频宽带吸声设计提供了有效思路。同时,复合材料格栅夹芯结构已经被证明是承载特性优良的结构形式,在格栅内附加吸声性能设计有望实现承载和隐身功能一体化设计。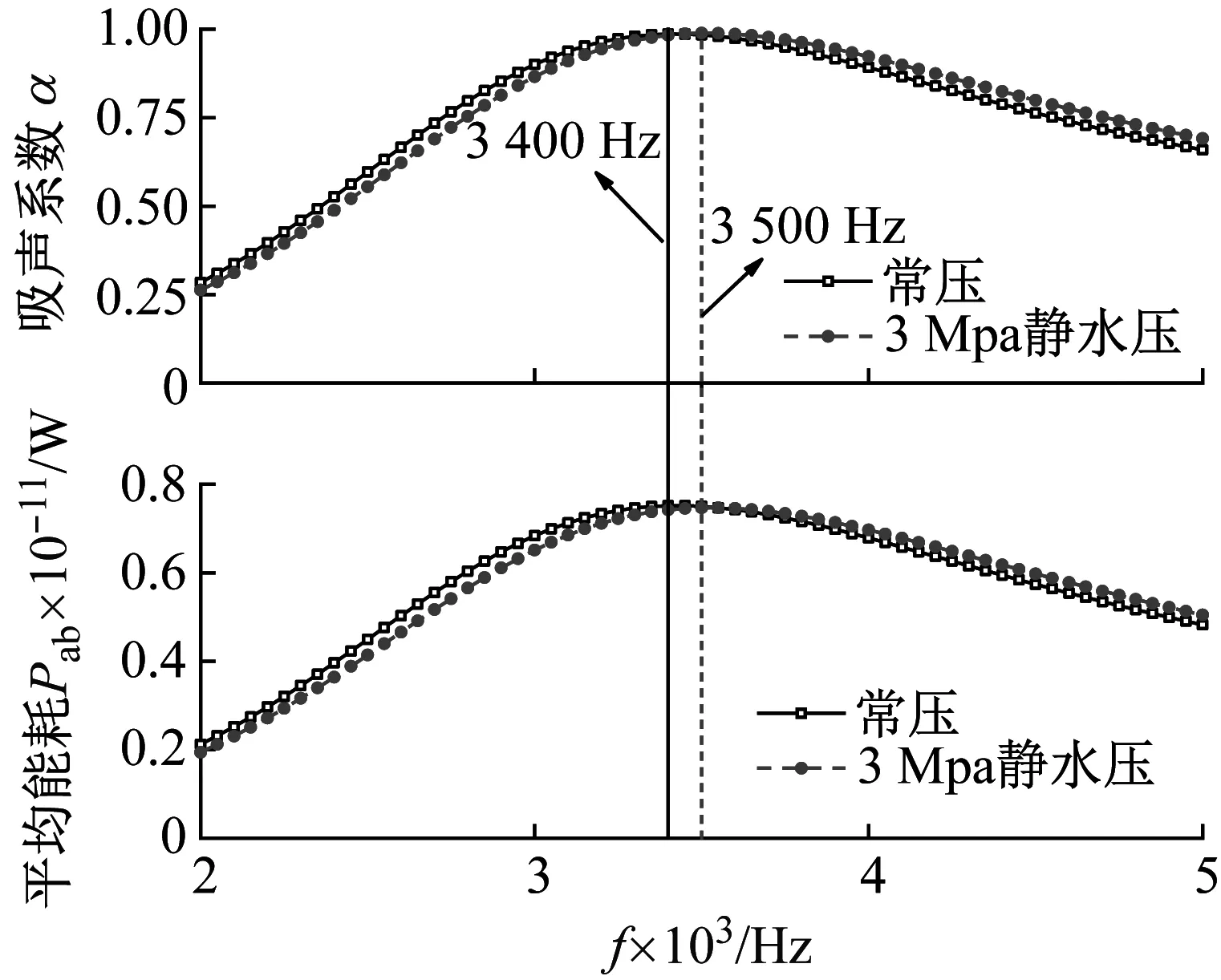


5 结 论

