含缺陷功能梯度压电材料的动态断裂行为分析
安 妮, 宋天舒, 赵 明
(1. 哈尔滨工程大学 航天与建筑工程学院, 哈尔滨 150001; 2. 东北电力大学 建筑工程学院, 吉林 吉林 132012)
为了满足自适应材料的特殊要求,功能梯度材料的概念被提出,并引起了人们的广泛关注。在很短的时间内,功能梯度材料的概念便从最初的高温元件扩展到了压电元件,目前功能梯度压电材料在电子技术、通讯和控制技术中均得到了广泛的应用。由于压电材料属于脆性材料,在生产或者加工过程中产生的孔洞、裂纹、夹杂等缺陷将在很大程度上影响材料的使用寿命,使得含缺陷的功能梯度压电材料的断裂特性的研究成为了热点问题。因此,本文对于含复合型缺陷的功能梯度压电材料的断裂问题的研究具有重要意义。
目前,国内外学者针对不同材料结构、不同缺陷形式、不同载荷作用下的功能梯度材料的断裂问题的相关研究已经十分广泛。按照所研究的结构形式由简单到复杂,可细分全空间功能梯度压电结构、半空间功能梯度压电结构、均匀压电材料与功能梯度压电材料粘接结构、两种不同的功能梯度压电材料粘接结构、功能梯度压电带、由中间层为功能梯度压电材料而上下层为均匀压电材料组成的三明治结构等。按照缺陷形式的不同,大体上可分为孔类缺陷、裂纹缺陷、夹杂缺陷等。其中裂纹的形式研究较多的为直裂纹,还有一些学者们关注弧形裂纹、环形裂纹和便士形裂纹的扩展问题。按照载荷形式的不同,被研究较多的通常有热载荷、电载荷、静载荷、冲击载荷、弹性波等。
20世纪60年代中期,Sih[1]较早研究了剪应力作用下裂纹体的应力分布问题,为此类问题的研究奠定了理论基础。21世纪初,Wang等[2]考虑了包含动态载荷作用下的一些非共线裂纹的渐变复合材料板的响应问题,利用拉普拉斯变换和傅里叶变换技术,得出了每一层的一般解。然后,通过引入边界条件和层界面条件来获得整个介质的解。该方法为层合结构的分析提供了思路。Ma等[3-6]采用Schmidt方法研究了在反平面剪切波作用下三明治结构中的共线裂纹问题、利用积分变换和微分因子法求解了功能梯度涂层-基体系统中的内部或边缘静动态裂纹问题。综合积分变换、留数理论和叠加方法,Guo等[7-8]针对功能梯度材料或功能梯度涂层结构中的垂直于表面的裂纹和共线裂纹的热断裂行为进行了分析。仲政等[9]对有关功能梯度材料断裂问题的理论与数值计算方法进行了综述。Ghafarollahi等[10]基于多极展开法,对界面附近的任意方向椭圆孔洞或裂纹对弹性波的散射问题进行了解析求解。李戎等[11]关注到含裂纹功能梯度材料的应力强度因子计算难以避免复杂的矩阵运算以及数值积分,他们对含外表面环向裂纹功能梯度材料圆筒,利用功能梯度材料圆筒与均匀材料圆筒裂尖应力的比例关系,将复杂的功能梯度材料圆筒应力强度因子求解问题转化为简单的应力值提取问题以及经验公式计算问题。
除了对稳态断裂问题的研究外,也有很多学者对瞬态断裂问题展开讨论。Guo等[12-13]采用Fourier和Laplace变换方法研究了含裂纹功能梯度层状结构的瞬态断裂行为。Bagheri[14]基于线弹性理论提出了两个具有界面Volterra-型螺旋位错的正交各向异性功能梯度半层在反平面瞬态载荷作用下的解析方法。以上大部分的分析均是在力电载荷、静载荷、冲击载荷、弹性波等的作用下展开的,而在扭转载荷、热载荷作用下的此类问题分析较少,Tavakoli等[15]应用分布位错技术从理论上分析均匀各向同性层与其功能梯度材料涂层之间的多个轴对称界面裂纹在扭转载荷下的断裂行为。程家幸等[16]研究了含微孔洞缺陷的压电功能梯度材料矩形板的热屈曲相关特性。
在实际工程中,压电材料的应用场合越来越复杂,一些学者开始转向研究功能梯度材料的混合加载问题以及压电压磁材料的力-电-热-磁多场耦合问题。Pathak[17]用扩展有限元法模拟了裂纹的不连续性,分析了在机械载荷和热载荷混合加载环境下的裂纹相互作用问题。Fang等[18-19]利用波函数展开法和镜像法研究了圆孔对反平面剪切波的散射问题。孙建亮等[20]利用Fourier变换方法对功能梯度压电压磁体中单个直裂纹的反平面剪切问题进行了详细的理论研究。用同样的方法,Bagheri等[21]研究了夹在两个磁电弹性层之间的功能梯度正交各向异性层的动应力集中问题。张超群等[22]利用传递矩阵法和Bloch定理,分析了界面损伤和损伤耦合对第一带隙特性的影响。夏振庭等[23]基于变分渐近法模拟了金属芯压电压磁纤维/聚合物基复合材料的有效时变,非线性和多物理场响应。赵星等[24]针对非理想界面功能梯度压电/压磁双材料中SH界面波的传播问题。Milan等[25-27]把处理力-电场中瞬态断裂问题的方法引入到求解力-电-磁多场耦合结构的瞬态断裂问题中。
可以看出,现有文献大部分关注FGPMs中单一缺陷的动应力集中问题、或单纯考虑对称缺陷问题,而研究多个缺陷相互作用问题的文献又大部分关注的是单一的弹性场,不涉及力电耦合问题。因此,为了研究含非对称复合型缺陷的FGPMs粘接结构在剪切波作用下的力学特性,本文将用于求解均匀压电材料断裂问题的方法引入到FGPMs的求解中,为含复杂缺陷功能梯度材料的多场耦合断裂问题提供方法和参考。
1 问题描述
本文考虑的双相功能梯度压电材料结构如图1所示。x轴的下方和上方分别为两种不同梯度的压电材料,材料性质分别沿y方向呈指数形式变化。将这两种材料沿着x轴粘接,在粘接面上存在一个半径为R0的圆形孔洞和长度为A的界面裂纹。假设一束时间谐和的力电波沿与x轴正半轴成α0角度入射到含缺陷的介质中,本文所要解决的问题是如何求解此类非均匀材料中复合型缺陷的动应力集中问题。

图1 功能梯度压电材料中由孔边激发的界面裂纹模型
1.1 控制方程
假设此粘接结构的弹性常数、压电系数、介电常数和密度在界面上同,分别为c440,e150,κ110和ρ0,介质I和介质II的非均匀参数分别为βI和βII。材料参数满足如下关系
(c44(y),e15(y),κ11(y),ρ(y))=
(c440,e150,κ110,ρ0)e2βy
(1)
对于此反平面问题,仅存在出平面位移和平面内电场,力电场表达式可以定义为[28]
F*(x,y,t)=F(x,y)e-iωt
(2)
式中,ω为入射波的圆频率。由于所有场变量均具有相同的时间因子e-iωt,故在后续的推导中将忽略此项,仅考虑场变量F(x,y)即可。
功能梯度材料的压电方程分量形式如下

(3)
在忽略体力和自由电荷的情况下,由弹性位移和电位势φ两个物理量表示的控制方程为
(4)
可以看出,控制方程中的位移和电位势φ耦合在一起,这将使得方程的求解非常复杂,因此,考虑引入一个合适的解耦函数来解决此问题,其满足如下关系
φ=φ-(e150/κ110)
(5)
将式(5)代入到控制方程(4)中可使和φ分别满足

(6a)
(6b)

1.2 电弹场的构造
本文考虑所研究问题的稳态解,令=0e-iωt,代入到式(6b)中可将位移满足的方程转换为
(7)
其中k为波数,满足关系k=ω/cSH。若式(7)的解的形式为=e-βyu(x,y),则u(x,y) 应满足方程
∇2u+K2u=0
(8)
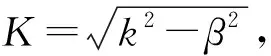
i=
r=
f=
(9)
上标i,r和f分别代表入射、反射和折射。α2为折射角。式(9)相应的散射位移场和电位势场分别为
is=
rs=
fs=
(10)
(11)
其中

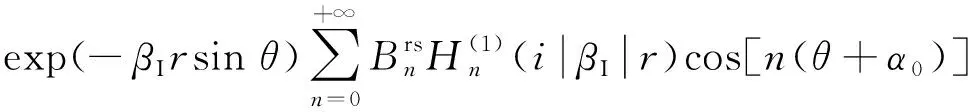
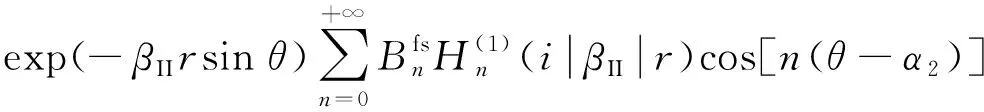
由于孔内仅存在电场,并无位移场,结合∇2φc=0可知孔内的电位势场φc(is,rs,fs)形式如下
(12)
接下来,以入射波为例,将式(9)~(12)代入式(3)相应的极坐标方程中可得出剪应力和电位移的表达式
φ=φi+φis=
(13)

(14)
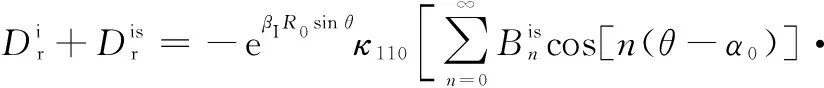
(15)
(16)
2 Green函数
在本小节中,采用Green函数方法来求解边界值问题。对于本文模型,所构造的Green函数为一个具有半圆形缺口的功能梯度压电介质弹性半空间在其表面任意一点r0作用时间谐和的出平面力电线源载荷时位移函数和电场函数的基本解,分别表示为

(17)
(18)
式中:G代表位移Green函数;Gφ代表电位势Green函数。由Sommerfeld辐射条件可知,孔内电位势应为有限值,故:
(19)
把式(17)~(19)代入式(3)的极坐标形式可以得到剪应力和电位移为

(20)
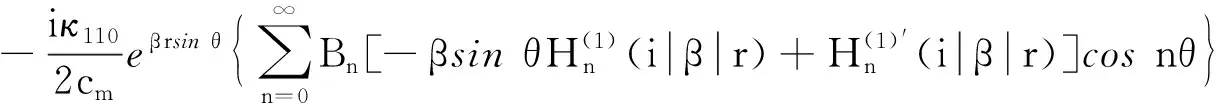
(21)
(22)
式中,κ0为真空(或空气)介电常数。由于在界面处,上半空间与下半空间的边界应力方向相反,故作用的线源激励方向也应相反,由此可知
(23)
3 边界条件与未知系数的确定
3.1 边界条件
圆孔边界面和裂纹面应满足电导通边界条件和应力自由边界条件,界面处应满足弹性位移连续、剪应力连续、电位移连续、电位势连续边界条件,即:
(24)
(25)
3.2 未知系数的确定
将式(12)~(16)代入到边界条件(25)中可得出求解入射波散射场未知系数的无穷代数方程组
(26)
其中

cos[n(θ-α0])


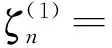
inεncos[n(θ-α0)]
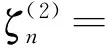
cos[n(θ-α0)]
将式(17)~(22)代入到边界条件(25)中可得出求解和Green函数未知系数的无穷代数方程组

(27)
其中
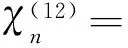
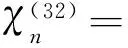
接下来,利用三角函数的周期正交性消除变量θ,将式(26)、(27)的两边同乘exp(-imθ)并在(-π,π)上积分,即:
(28)
(29)
4 积分方程与动应力强度因子
根据裂纹切割和界面契合的思想,可以构造出接近于真实裂纹的裂纹力学模型,如图2所示。
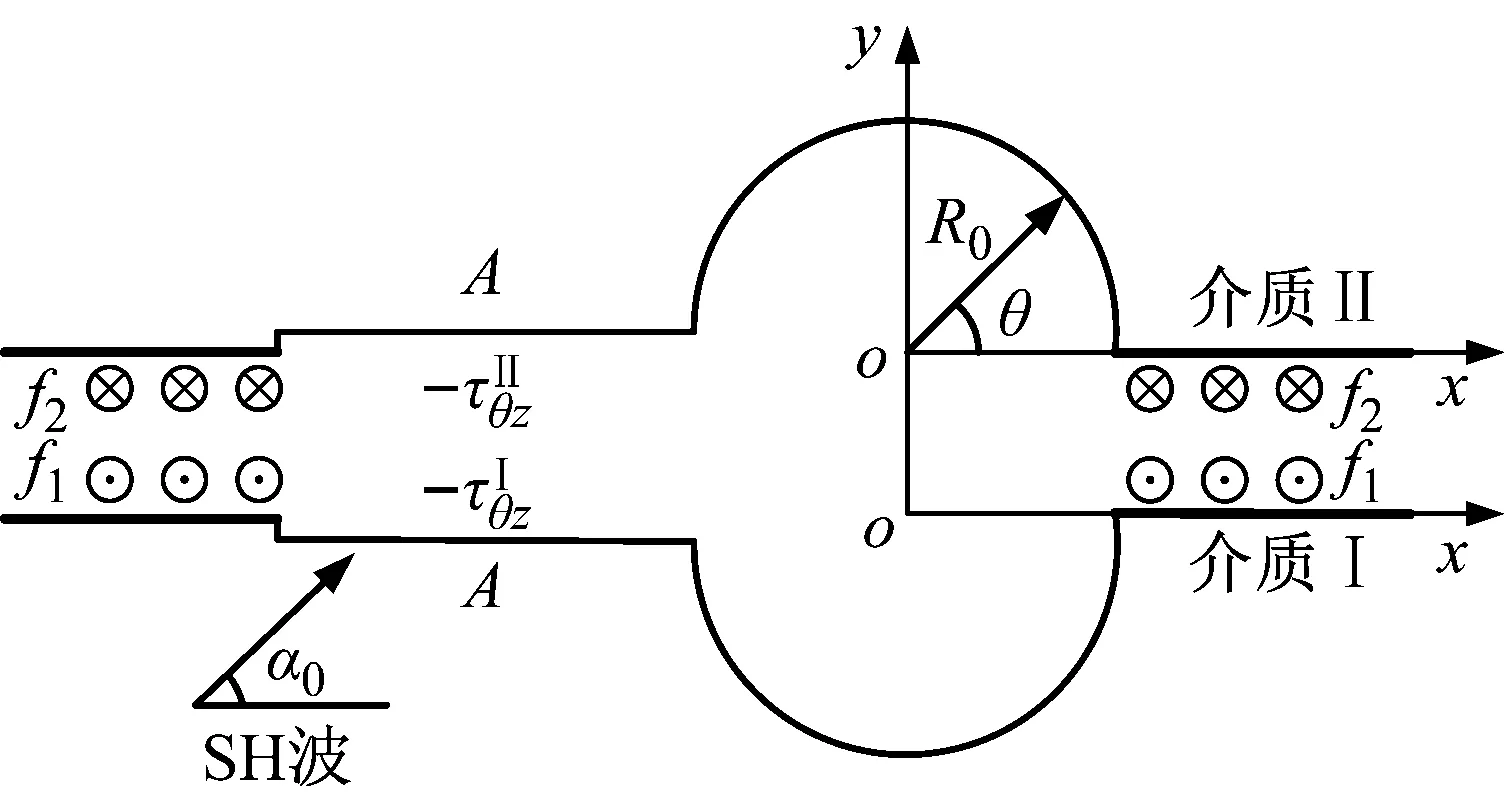
图2 上下半无限功能梯度压电介质的切割与契合
具体构造过程如下:
首先将双相功能梯度压电介质于界面处(x-轴)切割开,则切割面上的位移为
(Ι)(r,θ)=(i)(r,θ)+(is)(r,θ)+(r)(r,θ)+(rs)(r,θ)
(ΙΙ)(r,θ)=(f)(r,θ)+(fs)(r,θ)
(30)
剪应力为

(31)
式中



(32)
Ι(r,θ)+(f1)(r,θ)+(τI)(r,θ)=ΙΙ(r,θ)+(f2)(r,θ)+(τII)(r,θ)θ=0,r≥R0;θ=π,r≥R0+A
(33)
式中
将式(32)代入式(33)中便得到所求问题的积分方程

(34)
这里引入孔边径向裂纹的动应力强度因子公式
(35)
将式(34)中的被积函数做如下代换

(36)
则可知在裂尖处,即r0→R0+A时
(37)
这样代换后得到的积分方程将直接包含kIII,在理论计算中一般会定义一个无量纲动应力强度因子
(38)

5 数值算例
作为算例,本节给出了动应力强度因子(dynamic stress intensity factor, DSIF)随非均匀参数、入射波数、入射角以及缺陷几何尺寸的变化规律。为了验证理论方法的正确性,首先将本文模型退化成直裂纹,针对垂直入射的情况,与Guo等研究进行对比,结果如图3所示。可以看到两条曲线基本吻合,最大误差出现在kA=1.6处,误差值为1.21%,由于误差小于3%故可以认为采用本文方法求解功能梯度材料中复合型缺陷的断裂问题是有效的。接下来,为了说明孔的散射对裂纹尖端应力场的影响绘制了图4;图5~图7用于反映材料非均匀性和波数对DSIF的影响;图8用于分析缺陷几何尺寸对结果的影响;图9用于表明入射角度对DSIF的影响。

图3 本文退化模型与已出版文献[30]模型的对比

图4 缺陷总长度相等情况下本文结果与已出版文献[30]结果的对比

图5 功能梯度压电材料和均匀压电材料的对比

图6 DSIF随βI/βII和kR0的变化规律

图7 DSIF随kR0和β(βI=βII=β)的变化规律
图4给出的是当本文模型中裂纹和圆孔的总长度和文献[30]中的直裂纹长度相等时的对比结果。可以看出,随着孔半径的增加(与此同时裂纹长度的减小),裂纹尖端的DSIF越来越小,且孔径相对于裂纹的尺寸越大,DSIF值下降的越明显。这说明,为了简化计算而将复合型缺陷等效为直裂纹进行分析是不准确的,这种等效计算无法反映裂尖应力场的真实情况。
图5给出的是波数kR0=0.5和kR0=1.0两种情况下功能梯度压电材料与均匀压电材料的裂尖场DSIF对比结果。当非均匀参数值取图中数值的情况下:低频入射(kR0=0.5)情况下,功能梯度压电材料的动应力强度因子峰值比均匀压电材料高约34%;中频入射(kR0=1.0)情况下,两曲线峰值相差不大且走势接近。由此可知,当其他参数相同时,材料的非均匀性对裂尖应力场的影响在低频载荷作用下更明显。
图6给出的是不同波数情况下DSIF随材料I与材料II的非均匀参数比值的变化规律。按照当前参数的取值,可以看出,在中高频段DSIFs随βI/βII的增加而减小,且DSIF与βI/βII几乎成比例变化;在低频段,随着βI/βII的增加,DSIF先是缓慢增大,增大到材料I的非均匀参数为料II的非均匀参数的2倍时才呈现大幅度减小趋势。且kR0=1.0所对应的曲线一直比其他两条曲线高,说明对于FGPMs,中频段的动态特性分析更为重要。
图7给出的是两种材料梯度特性相同情况下的DSIF随波数和非均匀参数的变化规律。可以看出,均匀材料的DSIF峰值并不是最大的,当梯度参数值减小为负值时,DSIF的峰值要远比均匀材料的情况大很多。这说明材料的非均匀性并不总是增加裂纹尖端处的应力集中,适当的选取梯度参数反而可以降低结构破坏的可能性。
图8给出的是当裂纹长度与孔径的比取不同值时,DSIF随波数kR0的变化规律。可以看出当A/R0=1.0时曲线的峰值最大,且各曲线峰值基本位于中低频段,低频和高频作用下DSIF数值均较小。这说明当复合缺陷中孔半径与裂纹长度相近时孔的散射作用将加剧裂纹尖端的应力集中。
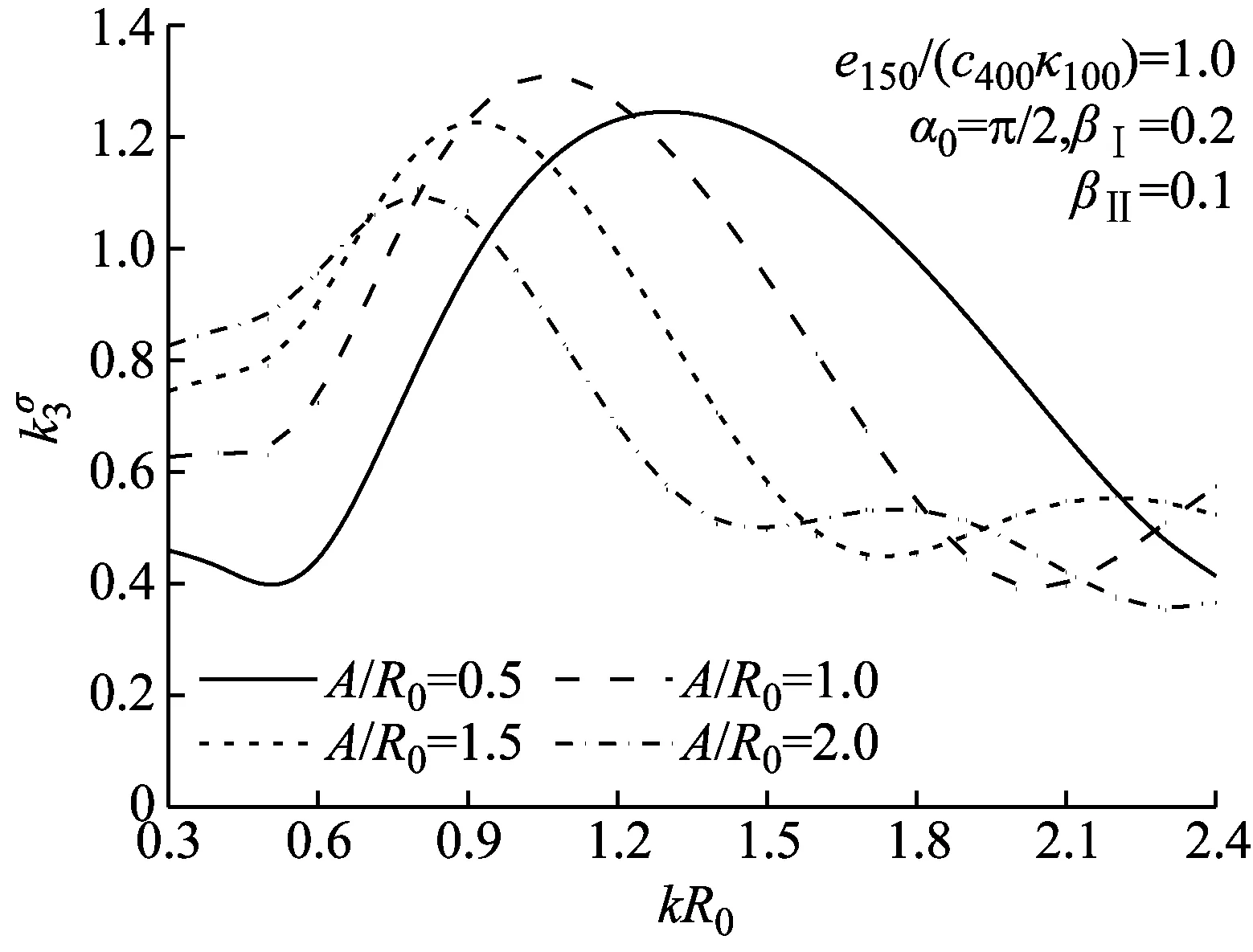
图8 DSIF随kR0和A/R0的变化规律
图9给出的是低、中、高频情况下DSIF随入射角度和上半空间非均匀参数的变化规律。显然,三幅图的峰值均对应βII取较大值的情况。低频和中频入射时,无论弹性波以何角度入射,DSIF均随βII的增大而增大;而高频入射时,入射角度为90°~135°时的规律正好与此相反。低频入射时的最危险入射角度在120°左右;中、高频入射时的最危险入射角度在60°左右。整体来看,随着SH波的入射角度的增加,频率越高,裂纹尖端的DSIF减小的越明显,这是由复合缺陷不对称导致的。
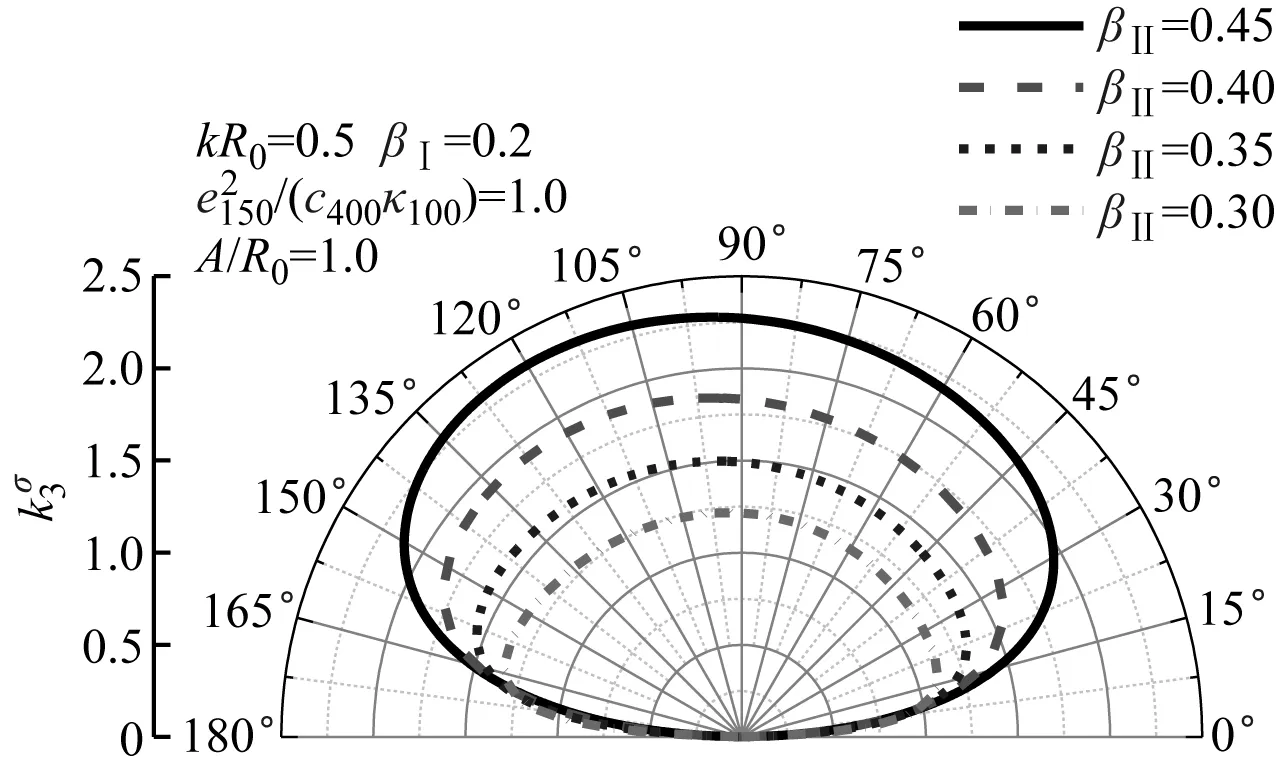
(a) kR0=0.5
6 结 论
本文针对反平面剪切波作用下含复合缺陷功能梯度压电材料的断裂问题,提出了一种基于Green函数的理论计算方法。通过引入解耦函数将电场和弹性场分离,推导出由界面和圆孔导致的反射波、折射波和散射波的具体形式,根据界面边界条件并结合裂纹切割和契合技术得到直接包含动应力强度因子的积分方程。对于实际工程中普遍存在的由缺陷导致的功能梯度压电元件失效问题,采用本文方法可以获得动应力强度因子的理论表达式,从而便于后续对裂纹扩展以及材料断裂等问题的研究。最后,通过数值算例详细分析了缺陷的几何特征、波数、入射角以及材料的梯度参数等对计算结果的影响。结果表明,基于Green函数方法在进行含复合缺陷功能梯度压电材料的反平面动态响应分析时具有较高的求解精度。

