基于组合赋权法的红河县地质灾害危险性评价*

周子涵，杨海林，钟延江

(1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2.中国电建集团昆明勘测设计研究院有限公司，云南 昆明 650051)

0 引言

地质灾害具有强隐蔽性和强破坏性的特点[1-2]。通过对地质灾害进行系统性的分析评价，判断区内地质灾害危险性程度，并根据危险区分布提前做好防治工作，可以避免或减少人员伤亡及财产损失，也可为地质灾害预警及灾后重建工作提供决策依据。

当前主流的地质灾害危险性评价方法分为定性方法和定量方法。定性方法主要基于决策者的主观判断及经验积累，评价结果具有较强的主观随意性，常见的定性方法有层次分析法、专家打分法等[3-4]。定量方法主要是对客观数据的理论分析，常见的定量方法有信息量法、熵值法、神经网络、支持向量机、逻辑回归模型等。定性定量模型的组合赋权法逐渐被用于地质灾害危险性评价。赵晓燕等[5]通过建立层次分析法和熵权法(熵值法)耦合模型，针对云南省东川区进行了地质灾害危险性评价，并结合斜坡单元的划分对危险性评价结果进行了检验，其结果与实际调查具有较高的吻合度。黄德镛等[6]提供了一种基于层次分析法和距离判别法的边坡稳定耦合模型，对边坡稳定状态进行了判别分析，与其他分析法相比，组合赋权法对边坡稳定状态判别具有更优解。

本文在红河县地质环境调查的基础上，通过对各类不同地质灾害孕育环境和发生条件进行分析，结合前人对该地的相关研究，通过主观评判的方式，选取9种具有普遍适用性的评价因子：地貌、高程、坡度、坡高、归一化植被指数(INDV)、岩性分布、与构造断层距离、年平均降雨量、与河流距离。运用层次分析法对上述因子进行主观权重的赋值，运用信息量-逻辑回归模型判断上述因子的显著性，筛除不满足显著条件的因子，再进行熵权法的客观权重赋值，最后运用层次分析法和熵权法组合赋权开展红河县地质灾害危险性评价，以期为红河县城乡发展规划、防灾减灾预警、灾后重建等工作提供参考，也可为类似地区的地质灾害防治提供借鉴。

1 研究方法

1.1 层次分析法

层次分析法作为一种主观赋权法，是通过将待评对象拆解为目标层-要素层-因子层[7-8]，根据各评价因子对地质灾害危险性的重要程度进行打分，建立判断矩阵，计算所得判断矩阵的最大特征向量，标准化得到权重矩阵W，对矩阵作一致性检验，即证明打分具有相对的合理性。

计算判断矩阵的最大特征值λmax，定义一致性指标CI和一致性比率CR：

(1)

(2)

式中，RI为平均随机一致性指标，1～9阶判断矩阵的RI值见表1。定义当CR<0.1时，判断矩阵通过一致性检验。

在判断矩阵通过一致性检验的前提下，通过一级评价因子权重计算对应的二级评价因子权重值：

(3)

式中，Na为各二级评价因子所含灾害点数，N为研究区灾害点总数，Wm为归一化后的一级评价因子权重值。

表1 平均随机一致性指标

1.2 信息量模型

信息量模型是以信息论为基础，通过统计分析诱发地质灾害的实测值，并将其转化为地质灾害危险性的信息量值，对各类评价因子提供的信息量进行加权分析，加权结果反映了各类评价因子对地质灾害危险性的贡献程度，信息量越高，则认为危险性系数越大[9-10]，其表达式为

(4)

(5)

式中，I为各评价因子Xi对形成地质灾害(H)所提供的信息量的总和，Ii(Xi，H)为各评价因子对地质灾害(H)所提供的信息量值，n为参评因子的个数，Ni为分布在某特定评价因子Xi内的地质灾害单元数，N为区内各处的地质灾害总数，Si为区内某评价因子Xi的分级单元面积，S为研究区域总面积。

1.3 逻辑回归模型

逻辑回归模型是二分类因变量(因变量y只取两个固定值)的回归统计分析模型[11]，可以描述因变量与自变量之间的关系。将区内地质灾害是否已发生作为因变量(0代表地质灾害未发生，1代表地质灾害已发生)、各类评价因子作为自变量(x1,x2,…,xm)，其中自变量可以是连续值或者离散值，不需要严格满足正态分布。按照每个指标的信息量值，建立研究区信息量-逻辑回归耦合模型。设研究区内各处发生地质灾害的概率为P，Q=1-P为地质灾害不发生的概率，将P/Q取对数即对P作Logit转换，记为LogitP，这样就保证了当概率在(0，1)中取值时，Logit转换值可以取任意实数。建立的回归方程为

(6)

式中：α为回归常数，βi(i=1，2，…，m)为回归系数，xi(i=1，2，…，n)为评价因子的信息量值。

得逻辑回归方程：

(7)

z=α+β1x1+β2x2+…+βmxm。

(8)

由信息量-逻辑回归耦合模型得到的各评价因子逻辑回归系数需满足显著性检验要求：显著性指标Sig.<0.05。移除不满足显著性检验的评价因子，重新计算信息量-逻辑回归耦合模型。

1.4 熵权法

熵权法是一种客观赋权法。按照每个评价因子的信息量确定权重，信息熵越大，信息的不确定程度越高，有效性越小，反之有效性越大[12-13]。诱发地质灾害的因素较多，不同诱因对地质灾害的贡献程度存在差异。因此本文考虑在建立信息量-逻辑回归耦合模型、排除显著性不足的评价因子的基础上，引入熵权法，降低极端值对结果的影响。熵权法确定贡献度的具体步骤叙述如下。

1)定义熵

(9)

式中：i为各二级评价因子；j为各一级评价因子；M为一级评价因子中各二级评价因子在研究区域内灾点密度分布的归一化指数，M∈[0，1]；E为一级评价因子的熵值。其中：

(10)

n为各一级评价因子下的二级评价因子分级数。

2)求熵权

(11)

式中，Wj为各一级评价因子权重系数，m为一级评价因子数。

3)加权叠加

(12)

式中，zi为第i项二级评价因子的逻辑回归值。

1.5 组合赋权

利用层次分析法确定主观权重时，忽略了大部分客观因素的影响[14]；而采用基于信息量-逻辑回归模型的熵权法确定客观权重时，忽略了一些主观因素的影响。因此，将层次分析法和熵权法结合，建立优化决策矩阵，可使评价结果更加合理。

设组合赋权为ω，得到组合赋权值：

ω=αωa+βωb，

(13)

式中，α和β分别表示主观权重和客观权重的偏好程度。

可根据欧氏距离函数建立差异程度方程确定α、β：

(14)

D(ωa,ωb)2=(α-β)2，

(15)

α+β=1。

(16)

2 研究区概况

红河县位于云南省南部、红河哈尼族彝族自治州西南缘(东经101°49′～102°37′，北纬23°05′～23°26′，海拔1 630 m)，距昆明市276 km，距州政府所在地121 km。

教学细节决定于教师本身的素质以及当时的教学过程和教学情境。教师面对特定的教学对象，有益的教学过程、形成的心理氛围，审时度势，为完成教学任务而采取相应的教学行为。在教学过程中，情境性也就意味着临场性、随机性和偶发性。许多教学细节是当时特定情境的特定反应行为，甚至于有些精彩的教学细节生成于特定情境中的偶发事件。

区内地层发育不全，地层连续性较差，以元古界哀牢山群及中生界三叠系地层出露最为广泛，其次为古生界志留系(S)、石炭系(C)及二叠系(P)，新生界新近系(N)及第四系(Q)地层。且由于区内多期构造运动和变质作用，地层发育多受断裂构造控制，接触关系多为不整合或假整合接触；县域处于著名的云南“山”字型构造建水弧顶前缘与哀牢山构造带中段复合区域，地质构造十分复杂，构造强烈发育。由于特殊的地理环境、复杂的构造背景和多变的岩性条件，导致红河县地质灾害频发(见图1)。

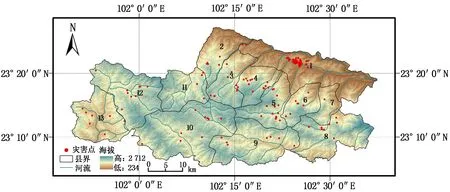
1-迤萨镇；2-大羊街乡；3-浪提乡；4-乐育镇；5-宝华镇；

3 危险性评价分区及结果分析

本研究所用的地质灾害数据来源于2019年云南省地质调查局组织的招标项目“云南省红河县地质灾害详细调查”，共有地质灾害点170处。与地质灾害危险性评价因子有关的基础数据包括：Landsat8 OLI影像(2015年2月7日、2017年7月3日)，ASTER GDEM数据(30 m 空间分辨率)，红河县1∶20万地质图，中国1∶25万一级，三级河流分级数据集，多年平均降雨量数据(2012-2017年)。

3.1 评价因子的选取与分级

地质灾害的暴发是内外部因子、自然与人为因素相互影响的结果。地质灾害危险性受多个因素的影响与制约，根据区内地质灾害的规模、种类、危险性、孕灾环境等，选择区内的地貌、高程、坡度、坡高、INDV、岩性分布、年平均降雨量、与河流距离、与构造断层距离等9个因子作为红河县地质灾害危险性评价指标，根据式(4)-式(8)建立各评价因子的信息量-逻辑回归模型，偏似然比检验结果显示，9个评价因子的Sig.均小于所设的显著性水平0.05(见表2)，说明这9个因子具有显著有效性，逻辑回归模型通过检验。

各评价因子分级结果如图2所示。

表2 逻辑回归分析结果

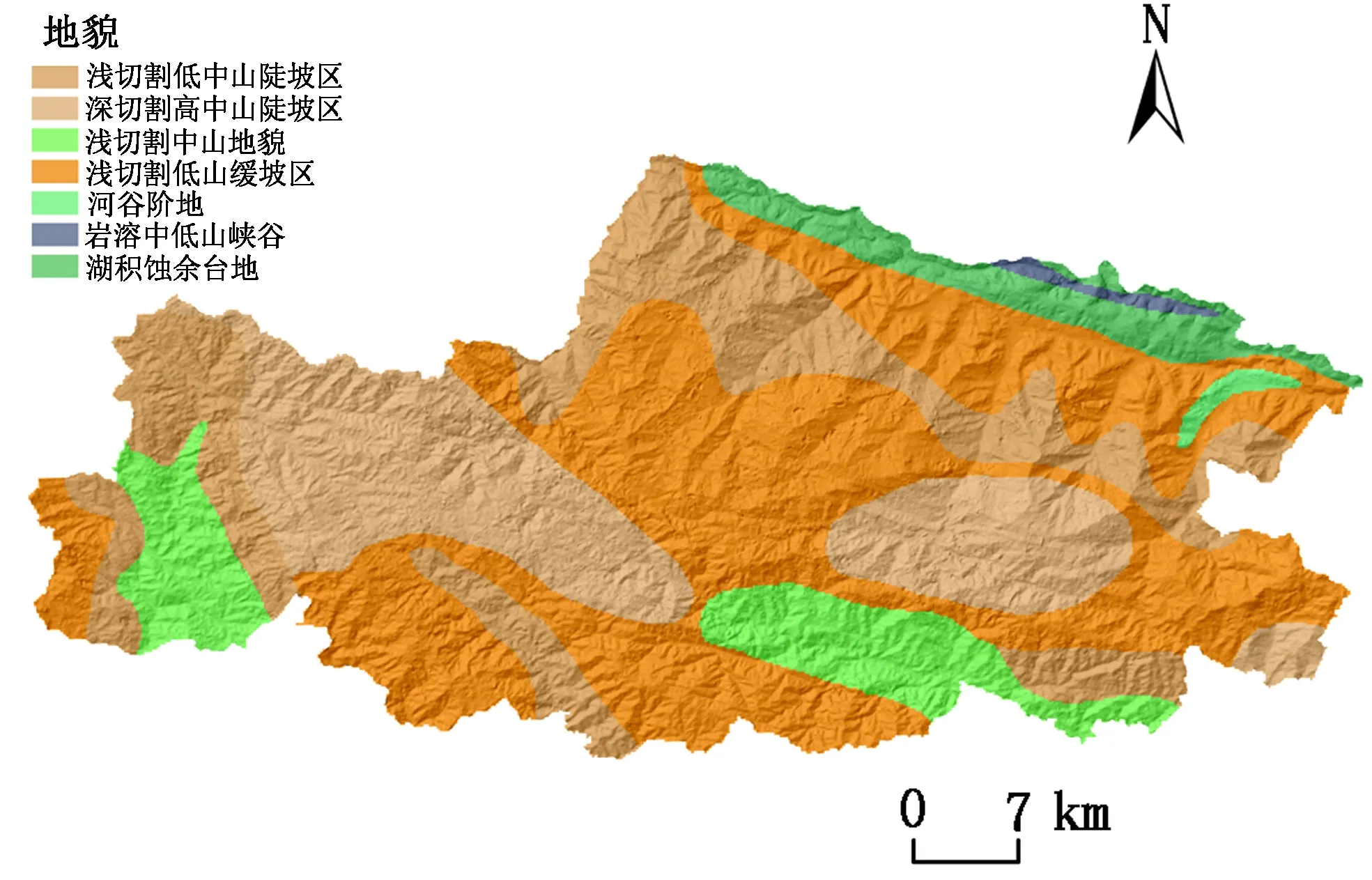
(a)地貌 (b)高程 (c)坡度/(°)

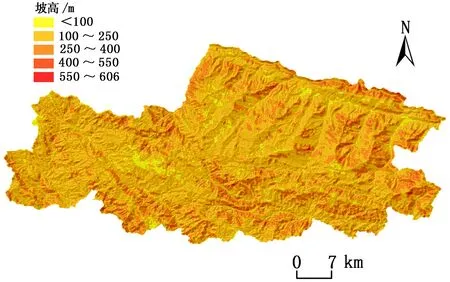
(d)坡高 (e)INDV (f)岩性分布

(g)与构造断层距离 (h)年平均降雨量 (i)与河流距离

1)地貌

地貌是地质灾害发生的控制条件[15-16]。本区地质灾害主要发生在侵蚀堆积地貌的亚类湖积蚀余台地和浅切割低山缓坡区，主要分布于北部红河河谷地带。该区主要为碎屑岩分布区，受干热河谷气候影响，降雨量少，单点暴雨强度大，风化及节理裂隙发育，地层较松散，坡面冲沟发育，中东侧局部有土林分布，为地质灾害高风险区。

2)高程

3)坡度

斜坡坡度对滑坡、崩塌等灾害的形成具有明显的控制作用。但坡度与地质灾害的发生不是单一的线性关系，在到达一定临界点后，较高的坡度并不利于坡积物堆积，物源不丰富，不利于灾害的形成。在本研究中，灾害集中发生在坡度小于30°的区域(占94.67%)，主要原因是缓坡区域便于人类生活和开垦耕地等，导致地表被严重改造。

4)坡高

坡高是单位面积内的高程最值差，反映了地表的起伏状况。坡度和坡高与包括重力在内的剪切力呈正相关。

5)INDV

植被能够增加土壤附着力，对松散岩土体有加固作用。一般情况下，高植被覆盖区的抗风化能力强，地质灾害发生率低。区内地质灾害危险点集中分布于北部低植被覆盖区(占31.95%)，主要原因是人类顺坡耕作、乱砍滥伐，导致水系紊乱，水土流失严重，生态环境恶化。调查显示，研究区内乡镇植被覆盖率最高仅为23.4%。

6)岩性分布

岩土体性质是衡量地质灾害危险性的重要因素之一，不同岩层结构的力学性质存在较大的差异，是地质灾害的物质基础和主控因子。由于区内多期构造运动和变质作用，地层发育多受断裂构造控制，岩性具有一定的不稳定性，岩体破碎、易风化和易泥化。同时，沿活动断裂带展布的动力变质岩、蚀变侵入岩等对外动力地质作用比较敏感，进而导致区内地质灾害频发。

7)与构造断层距离

构造发育地区岩体常呈破碎状，为地质灾害提供了丰富的物源。本文中与构造断层距离小于2 000 m的范围为地质灾害点相对密集区域。

8)年平均降雨量

降雨是地质灾害形成的主要诱因，雨水渗入岩层中，对泥质岩产生了浸润、软化的作用，使其摩擦力和黏聚力减小。此外，大量雨水冲刷会导致松散堆积体溃散，进而引发地质灾害。调查结果表明，区内降雨在时空分布上不均匀，大量降雨集中在5-10月，占全年降雨量的76%～84%，再加之各地地势起伏较大，导致区内降雨量与地质灾害活动强度、频度呈正相关。

9)与河流距离

区内主要河流有8条，灾害点在与河流距离小于600 m的缓冲区内集中分布，其他区域依次向两侧递减。调查结果表明，由于雨季雨量集中，地表径流剧增，山高坡陡，植被条件差，河道短，落差大，汛期洪水肆虐，是诱发滑坡、泥石流等地质灾害的主要因素之一。

3.2 评价结果及分析

根据式(1)-式(16)求出各指标权重，建立优化矩阵，确定各指标的组合权重，组合赋权各指标权重(见表3)。将主客观权重应用于优化矩阵，得到的最优组合权重为W=[0.125 5，0.176 2，0.050 4，0.047 0，0.116 5，0.116 1，0.162 2，0.150 1，0.056 0]。

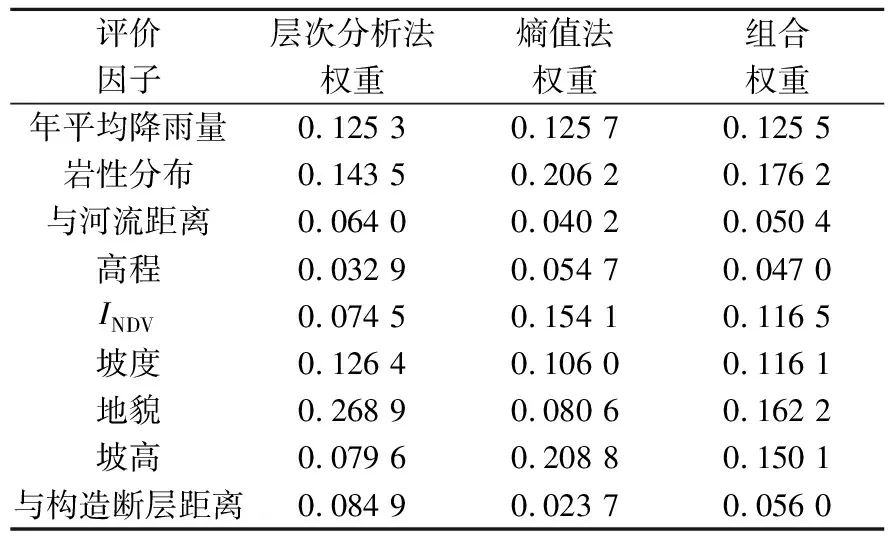
表3 组合赋权各指标权重

对所得的各类评价因子的组合权重进行叠加分析，使用自然断点法将地质灾害危险性程度划分为较低危险区、低危险区、中危险区和高危险区4个等级，得到红河县地质灾害危险性评价图(见图3)。对各等级危险区的面积和地质灾害点数进行统计(见表4)。由表4可知，中、高危险区的面积占总面积的63.34%，90.59%的地质灾害点落在中、高危险区内。经与实际地质调查报告对比，发现红河县地质灾害危险性分区具有较高的准确性。

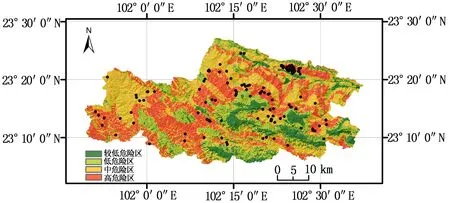
图3 红河县地质灾害危险性评价图

表4 各等级危险区的面积和地质灾害点数

3.3 评价精度检验

受试者工作特征曲线(Receive Operating Characteristic Curve，ROC曲线)是反映敏感性和特异性连续变量的综合指标，ROC曲线下的面积(AUC)越大，代表模型分类结果越准确，即模型精度越高。以地质灾害点的评价因子为样本，利用ARCGIS生成170个随机点，随机点与各灾害点的直线距离大于100 m，计算随机点的组合权重，进行ROC曲线检验，结果见图4。由图4可知，组合权重的AUC为0.840，表明组合赋权法对地质灾害危险性的划分具有较高的精度。

图4 地质灾害危险性评价模型ROC曲线

4 结论

a.以信息量-逻辑回归模型为地质灾害评价因子的筛选手段，确定了地貌、高程、坡度、坡高、INDV、岩性分布、与构造断层距离、年平均降雨量、与河流距离等9个评价因子。

b.采用层次分析法和熵权法的组合赋权，建立优化矩阵确定各因子权重，兼顾主客观因素，一定程度上避免了使用单一赋权法造成的评价结果的片面性。

c.对危险性分区和灾害点分布进行统计分析，将研究区分为较低危险区(12.48%)、低危险区(24.18%)、中危险区(33.98%)和高危险区(29.36%)，分区结果与实地调查结果具有较高的吻合度。

d.红河县地质灾害集中分布在北部地区，属于人类活动密集区，且地质环境脆弱，断层分布密集，危险性较高。