基于CRITIC-G1-TOPSIS法的爆破安全评价研究*

石海天，邓 飞，宋学朋

(江西理工大学 资源与环境工程学院，江西 赣州 341000)

0 引言

安全评价是预防工程爆破安全事故的重要环节，通过辨识爆破施工过程中的危险因素，可以发现安全薄弱环节，进而采取相应的预防措施，以降低重大事故发生的风险。目前关于工程爆破安全评价的研究成果较多[1]。徐志胜等[2]基于改进AHP法建立了多层次评价指标体系，并运用该体系分析了爆破施工安全模型，得出了该爆破工程的安全评价等级。于文贵[3]基于AHP-Fuzzy理论建立了模糊综合评价模型，通过分析水下钻孔爆破施工工艺，对工程项目进行了安全评价。

以上研究主要通过AHP法分析爆破安全评价体系中各因素的影响情况，然而AHP法比较的因素繁多，易导致如矩阵的一致性构造能力弱、标度值与排序方法不一致等问题[4]。与传统的AHP法相比，CRITIC-G1法既可以避免因重视主观经验而忽略指标之间内在关系的问题，又可以解决客观数据分析中因缺乏主观决策经验而导致权重不合理的问题[4]。鉴于此，本文利用G1法得到主观权重，利用CRITIC法获得客观权重，采用TOPSIS法对由主客观权重确定的综合权重进行分析，并对工程爆破安全体系进行综合评价，最终得出评价结果与正理想解的贴近度，据此判别爆破安全程度[5]。

1 爆破安全评价体系构建

影响爆破安全的因素包括定性因素和定量因素，本文参照相关文献及工程实际情况，基于层次分析原理，从安全4M(人为因素、管理因素、环境因素、技术因素)原则的角度出发[6]，建立工程爆破安全综合评价体系(见图1)。

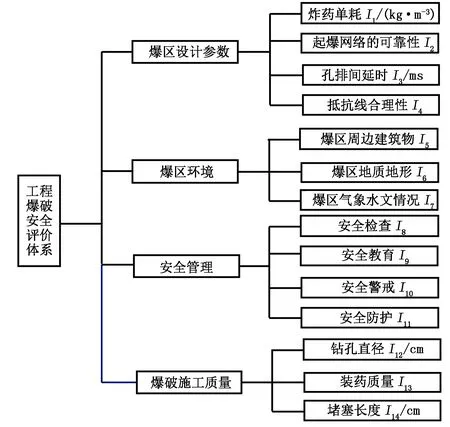
图1 工程爆破安全评价体系

2 CRITIC-G1法计算原理

2.1 主观权重的确定

通常采用AHP法确定主观权重，运用较多的计算方法是特征值法[7]，但是当被比较的指标数量较多时，会导致计算量庞大[8]。为了克服这一缺点，可采用无需一致性检验的G1法[9]，使主观权重的计算更加简便直接，计算步骤叙述如下。

当考虑某一评价标准时，如果指标Yi的重要程度大于Yj，则Yi>Yj。如果指标Y1，Y2，…，Ym对于某一评价准则有Yi>Yj>…>Yk(i,j, …;k=1, 2, …,m)，则指标之间的序关系为“>”。从指标集{Y1,Y2, …,Ym}中选出m个指标，并从m个指标中选出重要程度最高或者最低的某个指标Yi，将此步骤一直进行下去直至剩下最后一个指标，将其记为Yk，最后确定唯一的序关系[10]。

两相邻指标重要程度的比值计算如式(1)所示。根据前述的多个序关系计算出不同指标间的相对重要程度值[11](见表1)。

γk=φk-1/φk,k=m,m-1,…,3,2。

(1)

式中，φk表示第k个指标的权重。

表1 指标间的重要程度值

则

γk-1≥γk,k=m,m-1,…,3,2;

(2)

(3)

φk-1=γkφk,k=m,m-1,…,3,2。

(4)

2.2 客观权重的确定

CRITIC法是通过联合指标的相关性和信息量来确定指标权重的，既考虑了指标变异对客观权重造成的影响，又考虑了各指标之间的冲突[12]。用相关系数表征指标的相关性，相关系数越大则两个指标特征间的冲突性越低。用标准差来衡量指标的信息量，信息量越大则表明评价对象受该指标的影响程度越大[13]。CRITIC法计算步骤叙述如下。

建立评估指标矩阵X：

=(xj(ki))n×m，j=1, 2, …,n;i=1, 2, …,m。

用式(4)对矩阵作标准化处理，得到X*：

(5)

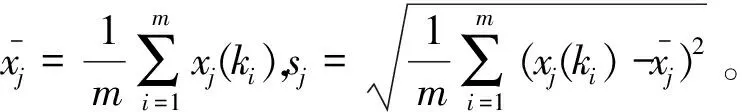
计算指标的变异系数：

(6)

利用式(5)得到X*的相关系数矩阵A=(ρtl)(t=1, 2,…,n;l=1, 2,…,m)，计算每列的(1-ρtl)值，得到行向量：

(7)

计算指标所含信息的综合度量hj以及客观权重Vj：

(8)

(9)

2.3 综合权重的确定

通过G1法与CRITIC法分别得到指标的主观权重与客观权重，结合两种方法的优点并充分考虑主观经验和客观规律的影响[14]，得到各评价指标的综合权重Vi：

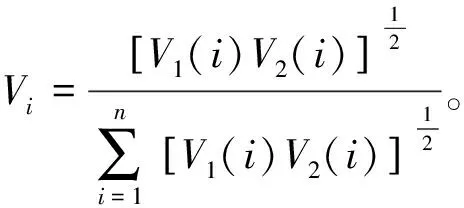
(10)

3 TOPSIS评价法

TOPSIS模型基于评价体系中的正负理想解，通过对每一个评价对象与正负理想解之间的距离和贴近度进行计算与排序，从而得出评价对象的优劣程度[15]。其计算步骤叙述如下。

(1)计算规范决策矩阵Zij

(11)

(2)构造加权规范矩阵Xij

Xij=Vj×Zi。

(12)

(3)确定正理想解和负理想解

正理想解记为Z+={maxzij|i=1,2,3,…,n}，

负理想解记为Z-={minzij|i=1,2,3,…,n}。

(4)计算各评价单元距正负理想解的距离

(13)

(14)

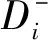
(5)确定各评价对象与理想解的相近程度

(15)

式中，Di表示第i个评价对象与正理想解的贴近程度，Di值越大，表明对象越优[16]。

(6)根据Di对各矿山进行排序，从而确定最优对象。

4 实例分析

新田萤石矿矿体岩层完整性较好，岩层产状平缓稳定，节理略发育，开采后东部北端形成直立陡坡[17]；石雷钨矿矿区属于丘陵地貌，山体总体呈北东走向，采用露天爆破自上而下开采，采剥面走向与矿体走向一致，梯段高差为15 m；武山铜矿矿区属于中低山区地貌，山体呈东南向延伸，坡度30°，矿带高50 m，平均厚5 m[18]。以新田萤石矿、石雷钨矿、武山铜矿的爆破开采为例，验证爆破安全评价模型的应用效果[19]。

通过调研相关文献及工程实际得到各评价指标的实测值(见表2)。由G1法计算得到的各指标主观权重见表3。

表2 各矿山爆破安全评价指标实测值

表3 各指标主观权重

根据CRITIC法建立评价指标矩阵X，对X作标准化处理得到X*，结合式(6)-式(9)，求出客观权重(见表4)。

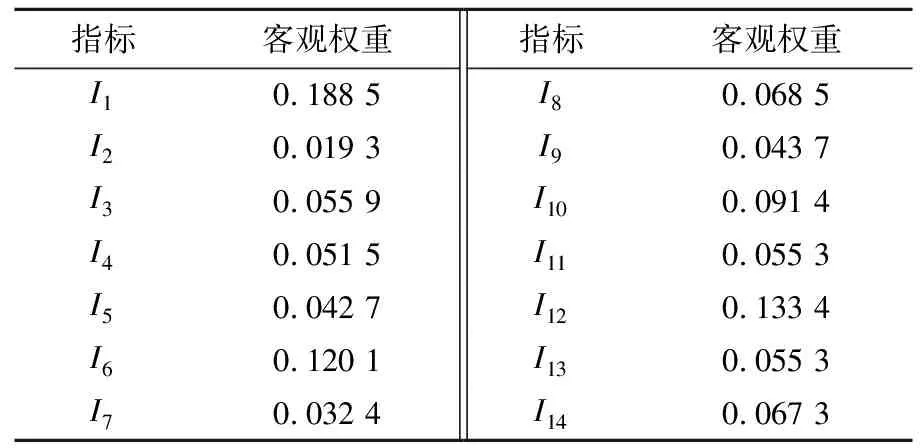
表4 各指标客观权重

用式(10)确定主客观综合权重Vi(见表5)。

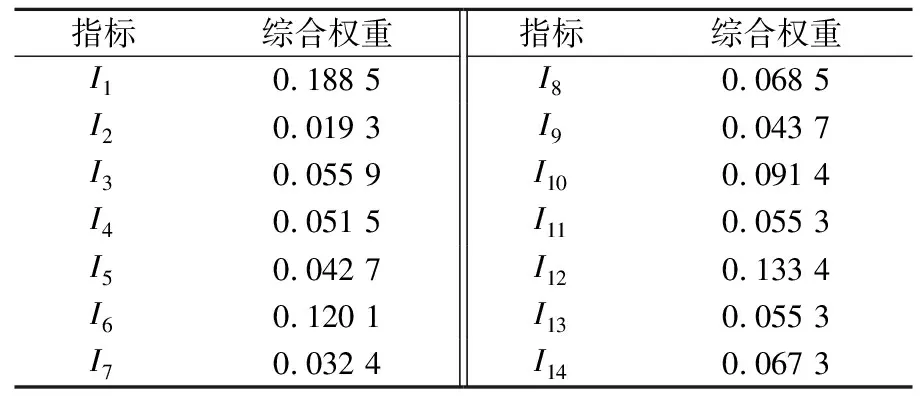
表5 各指标主客观综合权重

根据TOPSIS评价法，利用式(11)-式(15)，求得贴进度Di(见表6)。

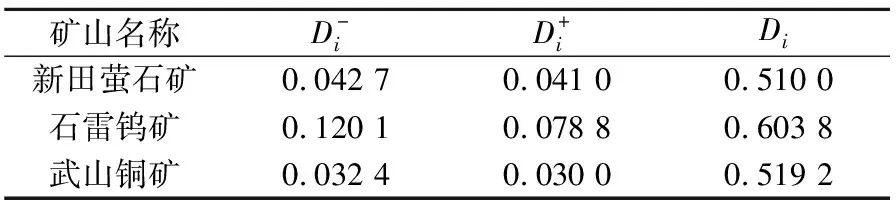
表6 工程爆破安全评价结果

由表6可知，新田萤石矿、石雷钨矿、武山铜矿的安全评价结果与正理想解的贴近度分别为0.510 0、0.603 8、0.519 2，即爆破安全评价结果从劣到优的排序为新田萤石矿、武山铜矿、石雷钨矿。

在爆破安全评价指标权重值一致的情况下[20]，新田萤石矿的爆破安全状况最差，主要原因是其爆破参数设计不合理、爆区环境较其他矿山差、爆破施工安全检查不充分。评价结果与AHP法的结果基本吻合，表明将CRITIC-G1-TOPSIS法用于矿山爆破安全评价是可行的。

5 结论

通过建立爆破安全评价体系，选取与爆破设计参数、爆区环境等相关的14项指标，根据CRITIC-G1-TOPSIS法计算得到新田萤石矿、石雷钨矿、武山铜矿的安全评价结果与正理想解的贴近度分别为0.510 0、0.603 8、0.519 2。该方法结合了相关经验与专家意见，兼顾了主观因素与客观因素的影响，提高了计算结果的客观性与合理性，为解决爆破安全评价问题提供了新思路。