基于自适应猫群算法的多目标波束赋形

林 峰，郑贾维，邵 羽，张长虹

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 电子信息与网络工程研究院，重庆 400065)

0 引 言

毫米波大规模阵列天线及其波束赋形是5G移动通信的关键技术之一，对提高频谱效率、减少小区间干扰具有重要意义。然而，毫米波技术的应用使得传统的智能优化算法及阵列方向图综合方法不再能满足用户对波束精度的需求。因此，为提高波束赋形的精度，如何设计一种更为有效的优化算法，已成为毫米波阵列天线波束赋形的关键问题。

目前，已有大量学者将智能优化算法应用到波束赋形中。文献[1]提出利用遗传算法查找幅度和相位最优值，但这种方法的收敛速度较慢。文献[2]提出利用粒子群算法寻找最优值，虽然其收敛速度快于遗传算法，但较容易陷入局部最优。为了进一步改进算法，文献[3]提出猫群算法(cat swarm optimization, CSO)，该算法在寻优过程中收敛速度快且具有较好的全局探测和局部搜索能力，可以很好地克服遗传算法局部搜索能力不足和粒子群算法易陷入局部最优的问题。文献[4]进行了猫群算法与遗传算法的性能比较，提出了一种改进的跟踪方法：在传统猫群算法的基础上，加入速度更新公式。通过对两个基准函数和一个背包优化问题仿真，得出猫群算法在收敛速度上优于遗传算法的结论。文献[5]提出一种二进制猫群算法，利用跟踪模式和搜寻模式交互来求解全局最优，对副瓣电平和主瓣宽度进行优化，并与二进制粒子群算法进行性能对比分析，仿真结果表明，二进制猫群算法的性能更优。文献[6]使用猫群算法对时间调制的圆环阵列进行优化，使其方向图获得更低的副瓣和更好的方向性，并把猫群算法与其他算法优化进行对比，验证了猫群算法的鲁棒性。可见，猫群算法在阵列方向图综合应用中具有较好的应用前景。由于大规模阵列天线的应用对阵列天线赋形性能的要求越来越高，传统的猫群优化算法的收敛性及全局寻优能力有待进一步提高。

为此，针对复杂的多目标赋形过程，提出一种自适应猫群算法(adaptive cat swarm optimization, ACSO)。首先，在搜寻模式中引入赌轮盘和精英选择相结合的策略，以增加种群多样性，提高局部搜索能力。其次，根据迭代次数和适应度函数值使用相关参数函数式自适应地调整算法参数，以提高算法的收敛性。通过对4种算法性能仿真对比，表明该算法收敛性得到提高且具有良好的全局寻优能力。最后，将该算法应用到2×8毫米波阵列天线多目标波束赋形中，提高了波束赋形的效率和精度。

1 猫群算法

猫群算法是一种基于猫的新型智能优化算法。在猫群算法中，大部分猫执行搜寻模式，少部分猫执行跟踪模式，两种模式通过猫的混合比率(mixture ratio, MR)相互切换。因此，猫群算法将猫的搜寻模式与跟踪模式相结合，实现了算法的全局优化。猫群算法的基本流程见图1。

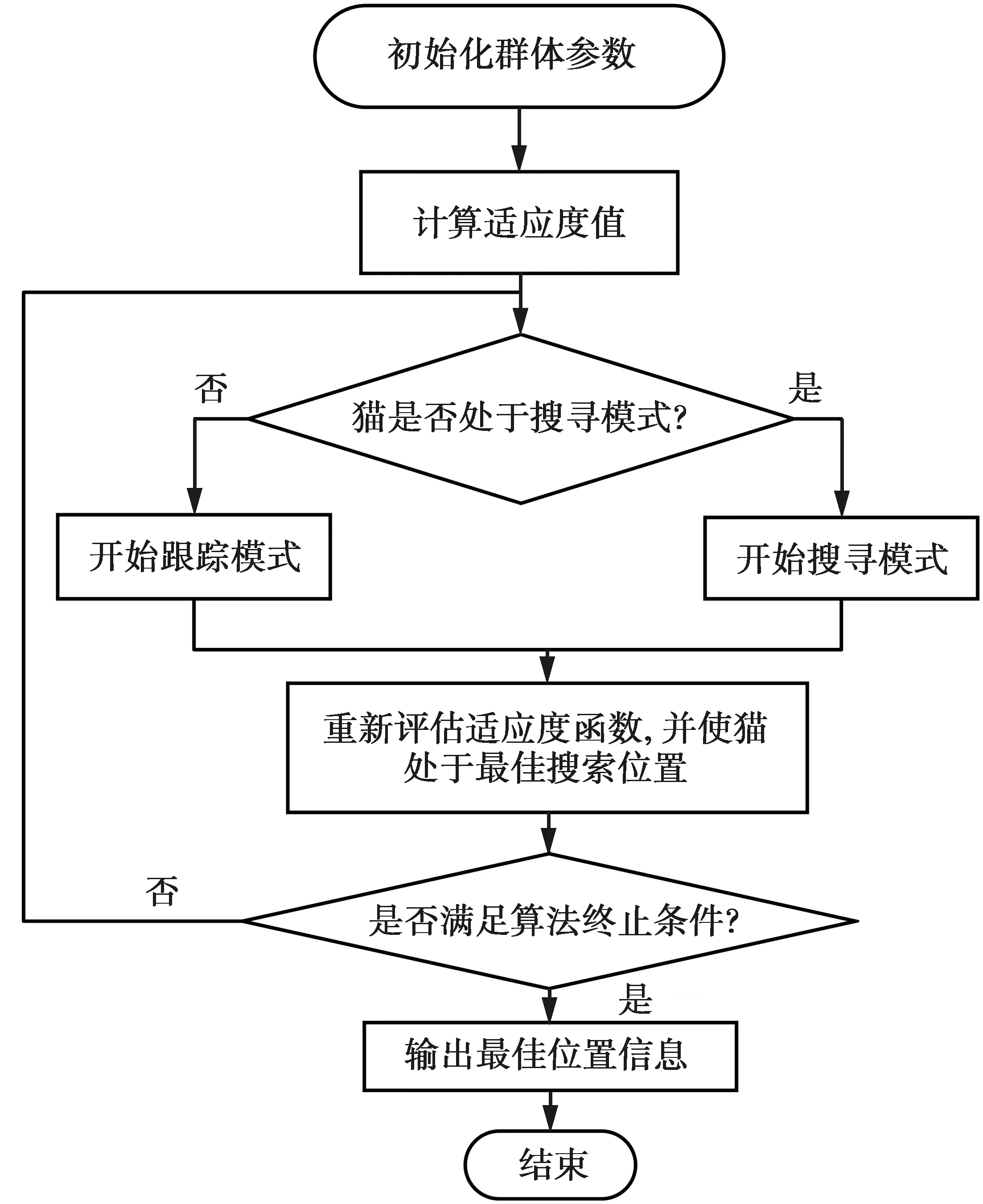
图1 猫群算法流程图Fig.1 Flow chart of cat swarm optimization

2 ACSO

为使多目标波束赋形能够更好地达到预期效果，在传统猫群算法的基础上进行改进，使其收敛速度和全局搜索能力更优。针对两种行为模式分别进行改进。

2.1 猫行为模式选择策略

混合比率MR值在传统猫群算法中是一个固定值，MR的大小决定了猫选择跟踪模式的比重，也就决定了算法的全局搜索能力。若MR过大，则局部搜索能力降低，反之MR过小，全局搜索能力下降，因此不论MR的大小如何选择，采用固定MR的猫群算法都不能合理有效地分配局部搜索和全局搜索的比重。本文采用一种根据迭代次数更新参数的方法[7]，使猫群算法在迭代前期采用较大MR的跟踪猫，以增加算法的全局搜索能力，在算法迭代后期选择较小MR值的跟踪猫，以提高解精度和算法收敛性。

混合比率MR的计算公式如下：

MR∈[0,1]

(1)

(1)式中：MRmax为混合比率最大值，MRmin为混合比率最小值，MaxIt为最大迭代次数，it为当前迭代次数。

2.2 搜寻模式

搜寻模式是用来模拟猫的当前状态：休息、四处探查、搜寻下一个目标位置。在搜寻模式中，包含4个基本参数，分别为：

1)搜寻记忆池(seeking memory pool, SMP)：主要用来暂存猫群在搜寻模式开始时复制出的与自身信息相同的猫，在每次迭代完成后，猫将从记忆池中选择适应度值合适的猫。

2)维度变化域(seeking range of selected dimension, SRD)：该数值通常为固定的百分比，用于改变搜索维度，使新旧值之间的变化不超过定义的范围。

3)维度变化数(counts of dimension change, CDC)：表示变异的维度个数，其取值范围为0到最大维度数。

4)自身位置判断(self-position consideration, SPC)：是一个布尔值，表示是否将猫经过的位置作为候选位置，取值为0或1。

为更好地权衡算法的收敛速度和收敛性，本文提出对搜寻模式中副本复制次数SMP、维度变化数CDC根据适应度函数值自适应调整的方法。根据迭代搜索原理，在较好适应度函数值的猫所在的局部区域，存在可更新全局最优猫的概率较大，此时增加SMP、CDC的值，可以增强局部寻优能力。而在较差适应度函数值的猫所在局部区域，存在可更新全局最优猫的概率较低，此时减少SMP、CDC的值可以减少算法运行时间。因此，相对于传统猫群算法中使用固定的SMP、CDC值的方法，根据当前适应度函数值大小调整SMP、CDC值可以在一定程度上提高算法的收敛性。针对本文中的ACSO，将适应度函数值归一化后划分为5部分，其对应的SMP值分别为12，10，8，6，4。同时CDC的值也被划分为5部分，分别为总维度的90%，90%，90%，80%，80%。

其次，为了进一步提高局部搜索能力，在搜寻模式中结合赌轮盘与精英选择算法以增加算法在初始阶段种群的多样性，并采用随机布尔运算法则，对这两种方法进行随机选择。

ACSO的搜寻模式具体流程如下。

步骤1根据适应度函数值计算当前猫所处位置的SMP值和CDC值；

步骤2将猫的当前位置复制SMP份，并根据SPC值判断是否保留当前值作为候选解；

步骤3对每个副本，针对现阶段的CDC值，给相应维度的猫加上或减去SRD值，并覆盖旧值，更新记忆池；

步骤4计算此时所有候选解的适应度函数值；

步骤5计算所有候选解的选择概率，及最优解的位置，并根据改进的候选解策略，按照随机布尔运算法则在2种策略中任选一种，输出该策略下猫的位置，替换搜寻模式猫的初始位置。

2.3 跟踪模式

跟踪模式下猫的活动轨迹与粒子群算法相似，在猫群算法中，猫进入跟踪模式，会以每一维上的速度进行移动。通常情况下会在速度更新公式前加入惯性权值，从而提高算法的收敛性。惯性权值大小影响算法的全局搜索能力和局部搜索能力。因此，为权衡两者性能，对惯性权值进行自适应调整。文献[8-9]提到将惯性权值根据迭代次数的增加而减少，但这种方法并不总是适用。为更快找到全局最优解，将惯性权重随着适应度函数Fitness单调地减少，因此，定义如下映射函数：

∀Fitness∈[0,1]

(2)

惯性权重的初始值为0.9，在跟踪前期较大的适应度函数值Fitness可以提高全局搜索能力，随着Fitness值的逐渐降低，局部跟踪能力得到提高。

ACSO的跟踪模式具体过程如下：

步骤1对每只猫按照式(3)更新其当前迭代的每一维速度；

v(t)=w×v(t-1)+r×c1×

[Xbest(t-1)-X(t-1)]

(3)

(3)式中，Xbest(t-1)为上一次迭代后适应度函数值最优的猫位置，X(t-1)为上一次迭代猫的位置，c1为常数，r的取值范围为[0,1]，w为惯性权值，如(2)式所示，根据适应度函数自适应调整以提高算法的收敛性。

步骤2对当前每一维速度进行判断，如超出边界，则取边界值；

步骤3根据速度更新值确定当前猫位置。

自适应猫群算法的流程见图2。

2.4 算法性能仿真分析

波束赋形的优化算法仿真主要在Matlab中实现，算法的性能指标主要包括算法的收敛速度、收敛精度、稳定性以及对误差的正确判断性。遗传算法和粒子群算法是波束赋形常用的优化算法，都是在自然特性的基础上，通过模拟个体种群的适应性，对空间进行搜索，从而得到最优解。

图2 自适应猫群算法流程图Fig.2 Flow chart of cat swarm optimization

为此，本文主要针对以下4种算法对比分析：遗传算法(GA)、粒子群算法(PSO)、猫群算法(CSO)、自适应猫群算法(ACSO)。为了比较4种算法的收敛和寻优能力，对表1所示的2种基准函数进行仿真测试，算法种群规模均设置为60，最大迭代次数均设置为800。

本算法在Matlab2016b平台上进行仿真，其操作系统为windows8.1，运行内存为8 GHz。算法独立运行20次，记录多次运行仿真后适应度函数收敛值的平均值、最优值、最差值和标准差，仿真结果见表2。为了验证ACSO的收敛速度，对CSO及ACSO迭代次数为800时的仿真时间进行测试，算法独立运行20次，仿真结果见表3。此外，由于本文所提到的毫米波阵列天线多目标波束赋形的适应度函数表达式与基准函数Sphere表达式较为一致，为了验证ACSO在多目标波束赋形应用中的可行性，对基准函数Sphere进行4种算法的收敛性测试，仿真结果见图3。

表1 基准函数

表2 各算法收敛精度对比

表3 猫群算法与自适应猫群算法收敛速度对比

图3 各算法针对基准函数Sphere的收敛性仿真结果图Fig.3 Convergence simulation results of each algorithm based on Sphere

由表2—表3可知，ACSO得到的最终适应度函数值均优于其他3种算法，并且当迭代次数为800时，ACSO的收敛速度优于CSO。此外，从图3可看出，针对基准函数Sphere的仿真测试，ACSO在77代时已收敛，而猫群算法、粒子群算法和遗传算法分别在123代、225代、345代才收敛，从而验证了ACSO在多目标波束赋形中的可行性。由此可看出，与CSO相比，ACSO具有更快的收敛速度和更强的全局寻优能力。

3 基于ACSO的波束赋形

3.1 波束赋形基本流程

随着5G毫米波大规模阵列的出现，阵元间耦合效应随之增加，传统的波束赋形方法已不能满足波束赋形精度的要求。为了减少阵元间耦合，在各个阵元间加入等间距的由基片集成波导(substrate integrated waveguide，SIW)构成的金属腔[10]，并且采用本征激励法[11]进行阵列方向图综合。

然而，对于大型阵列，本征激励法使得数据导出过程变得更加繁琐，为此提出一种针对大型阵列联合调用的波束赋形方法。在Matlab与HFSS联合调用过程中，通过HFSS的VBA宏语言与Matlab连接，利用Matlab中函数工具包产生脚本，调用HFSS软件，使得天线优化设计工作独立地在Matlab软件中实现，建模、求解、仿真工作在HFSS中自动完成[12]。此外，使用Matlab数值计算功能，对天线设计中的变量进行算法优化，并将优化结果返回HFSS进行仿真，循环调用后得到最优解。Matlab与HFSS联合调用的基本流程见图4。

图4 Matlab与HFSS联合调用的基本流程图Fig.4 Basic flowchart for joint invocation of Matlab and HFSS

首先，在HFSS中对天线单元进行建模，并在HFSS中建立2×8的天线阵列。对每个阵元的端口以集总端口馈电，集总端口的阻抗为天线单元在中心频点35GHz的阻抗，以此进行全波仿真。其次，仿真完成后，将Edit Source下激励端口的幅度和相位设置为变量。使用Matlab调用HFSS，将仿真后每个阵元被单独激励时的方向图数据以.csv文件格式导出，通过Matlab进行数据提取，并且根据阵元与阵因子方向图乘积原理，综合出阵列的方向图。最后，使用ACSO对幅度和相位进行优化仿真，并将优化的结果导入到HFSS中进行验证，如果未得到期望方向图，则调整适应度函数中各个子目标函数的权重，直至获得期望方向图，程序结束运行。

3.2 波束赋形仿真验证

为了验证算法的实用性，本文选取文献[13]中的毫米波电磁偶极子微带天线作为阵元，并且在电磁仿真软件HFSS中构建一个如图5所示的2×8阵列天线仿真模型。该阵列中心频率为35 GHz，拥有16个阵元，各个阵元等间距分布，间距为0.7λ(6 mm)。为实现良好的圆极化特性，使第一排阵列与第二排阵列空间旋转90°，相位相差90°。由于本文仅针对阵列的俯仰面进行波束赋形，所以只需优化第一排8个阵元的幅度和相位，而第二排8个阵元的幅度与第一排相等，相位调整成与第一排相差90°。波束赋形仿真结果如图6所示。

图5 毫米波阵列天线模型Fig.5 Model of millimeter wave array antenna

本文多目标赋形包括阵列余割平方方向图[14]、低副瓣以及较好的圆极化特性。针对优化目标，将适应度函数设置为：

Fitness=a×fitness1+b×fitness2+c×fitness3

(4)

(4)式中：fitness1是实际方向图与如图6a所示的余割平方目标方向图函数的差的平方函数；fitness2是实际方向图的副瓣电平值与目标低副瓣电平值的差的平方函数；fitness3为实际方向图轴比赋形范围内最大轴比与轴比优化目标值的差的平方函数；a、b、c分别为各个子目标函数的权值，此次赋形中a=0.56，b=0.32，c=0.12。

图6 波束赋形仿真结果图Fig.6 Simulation results of beamforming

使用HFSS对阵列进行全波仿真，并且选取各个阵元的幅度和相位作为优化变量，用HFSS与Matlab联合调用的方法提取各个阵元的远场方向图，使用ACSO在Matlab中优化各个阵元的幅度和相位。针对本次赋形，初始化算法参数MRmax=0.9，MRmin=0.1，MaxIt=800，SRD=0.5，SPC=1，r=0.5，c1=2。首先，根据(4)式计算适应度函数值，并且保存最优函数值的猫。然后，根据(1)式计算MR值，随机分配猫的行为模式，进行首轮迭代。此时，进入搜寻模式的猫，根据适应度函数值自适应调整SMP，CDC值，采用新的候选解策略选择此次迭代后的猫；进入跟踪模式的猫，根据(3)式更新当前猫的速度及位置。最后，当16只猫完成自身行为模式后，计算16只猫的适应度函数，并且选择最优适应度函数值的猫，再根据(1)式计算MR值，进行新一轮的寻优。经过多次迭代后保存适应度值最优的猫，从而得到满足赋形要求的幅度和相位，如表4所示。将优化的结果导入到HFSS中验证。仿真测试30次，选择最优赋形结果。为了更好地说明ACSO在阵列天线多目标波束赋形应用中的有效性，本文对GA、PSO、CSO及ACSO 4种算法在多目标波束赋形应用中的迭代收敛性进行仿真测试，测试30次，选择各个算法最优收敛结果，仿真结果见图7。

表4 各个阵元幅度和相位优化结果

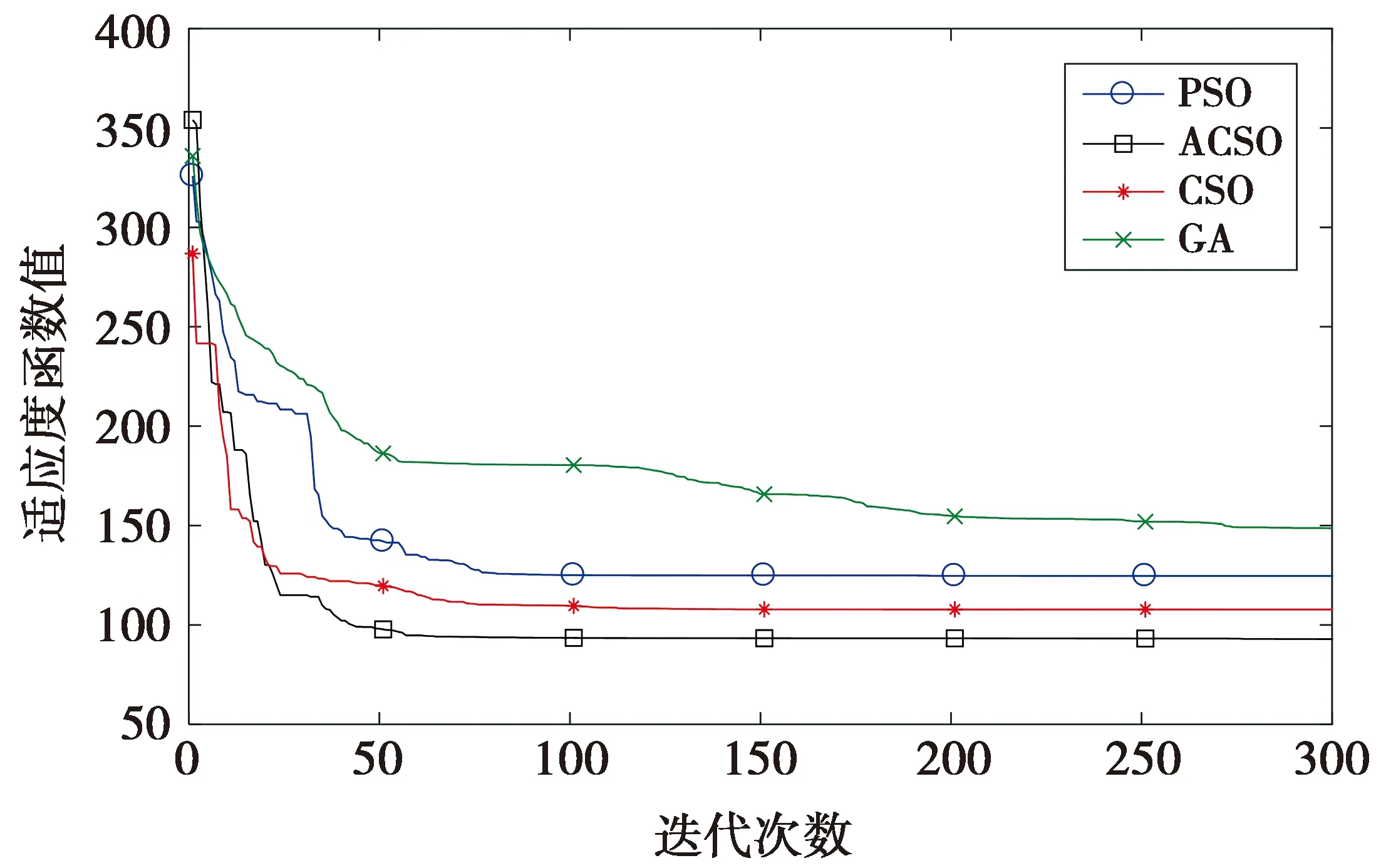
图7 多目标波束赋形中4种算法迭代收敛仿真结果图Fig.7 Simulation results ofiterative convergence for four algorithms in multi-objective beamforming

仿真结果表明，ACSO收敛精度优于其他3种算法，赋形结果满足目标设计要求。余割平方波束主瓣覆盖范围为[-15°,40°]，副瓣电平低于-13 dB，轴比小于3 dB的范围由原来的10°提高到21°，获得了良好的圆极化特性。此外，与文献[15]赋形结果相比，ACSO在赋形优化时综合考虑了阵元间耦合效应的影响，提高了波束赋形精度，同时也验证了其在毫米波阵列多目标波束赋形中的有效性。

4 结束语

本文针对阵列天线波束赋形中智能优化算法收敛性不高、收敛速度不快等问题，提出了ACSO。在传统猫群算法的基础上，使ACSO中的基本参数随着迭代次数或适应度函数值自适应改变，并在搜寻模式中加入赌轮盘和精英选择相结合的策略。基准函数测试表明，ACSO提高了CSO的收敛性和收敛速度。同时，ACSO在毫米波阵列波束赋形的应用中取得了较好的赋形效果，验证了其在多目标波束赋形中的有效性。