周期随机捕食-食饵系统的周期解的存在性

黄幼林，魏春金，张树文

(集美大学理学院，福建 厦门 361021)

0 引言

近年来,种群关系是生物数学研究的一个方向,对捕食-食饵模型的研究己经成为生物数学领域的热点之一，许多学者对其进行了深入的研究,并取得丰富的成果[1-4]。但实际上,各种随机干扰随处可见,它是生态系统中必不可少的重要组成部分。出生率、死亡率、环境最大承载量和其他参数都会受随机扰动的影响[5]。具有随机扰动的种群动力系统具有丰富的动力学行为,因此受到生物数学研究者的青睐。

在实际的生态系统中,周期现象普遍存在。比如种群受到昼夜更替、四季更替、个体生命周期、食物供应等的影响[6],出生率、死亡率和其他系数并不是保持一成不变的,而是可能会呈现一定的周期性[5]。因此，研究具有周期系数的动力学系统也是非常重要的。

文献[7]在研究害虫管理时提出了一个捕食-食饵模型假设:随着食饵密度的增加,捕食者种群将会逐渐消耗更小比例的食饵。该基础模型为

(1)

其中：x,y分别表示食饵和捕食者在t时刻的种群密度;r表示食饵的内禀增长率;b表示捕食者的捕获率;d表示捕食者的死亡率;λbx/(1+bhx)是Holling Ⅱ功能反应函数,λ和h分别表示营养转化率和处理时间;所有参数都是正数。文献[7-9]在这个基础模型上考虑脉冲作用,进一步研究了系统的种群动力学行为。基于模型(1)和上述工作,考虑了密度制约项，即

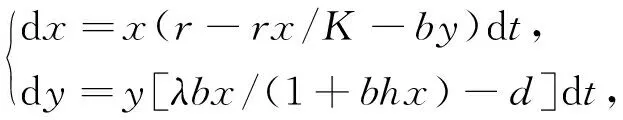
(2)

其中K>0表示最大环境容纳量。Sun等[2]在系统(2)中考虑经济阈值,研究系统的动力学性质,对害虫管理提供了一定的参考。

本文考虑下列带有密度制约与随机干扰的捕食-食饵模型的非自治系统，有

(3)

文中,总假设(Ω,F,{Ft}t≥0,P)是一个带有滤子Ft并且满足通常条件(即{Ft}t≥0是右连续单调递增,且F0包含所有零测集)的完备概率空间。

1 预备知识

随机微分方程

dx(t)=f(x(t),t)dt+g(x(t),t)dB(t)

(4)

的解记作x(t)=(x1(t),x2(t),…,xn(t))(t≥0),其中:f∈L1(Rn×R+,Rn);g∈L2(Rn×R+,Rn×m);B(t)是n维布朗运动。

定理1[10](存在唯一性定理) 假设f(x(t),t)和g(x(t),t)关于x(t)满足下列条件：1)局部Lipschitz条件，存在ck>0(k=1,2,…),使得∀x,y∈Rn且|x|∨|y|≤k有不等式|f(x,t)-f(y,t)|∨|g(x,t)-g(y,t)|≤ck|x-y|成立;2)线性增长条件，存在c>0,使得|f(x,t)|∨|g(x,t)|≤c|1+|x||,∀(x,t)∈Rn×R+,则初始条件为x(0)=x0∈Rn的系统(4)存在唯一连续的局部解x(t)(t∈[0,τe),τe是爆破时间)。

定理2[10](It公式) 设x(t)(t≥0)是It过程,其随机微分为dx(t)=f(t)dt+g(t)dB(t),其中：f∈L1(R+,Rn);g∈L2(R+,Rn×m)。若V(x(t),t)∈C2,1(Rn×R+;R),则V(x(t),t)仍然是It过程,具有如下随机微分：dV(x(t),t)=Vt(x(t),t)dt+Vx(x(t),t)dx(t)+dxT(t)Vxx(x(t),t)dx(t)/2。

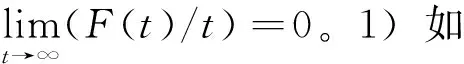
考虑方程

(5)

假设下列条件成立：

(6)

(7)

其中B是一个常数。

引理3[16]设方程(5)的所有系数关于t是T周期的,且在每个柱形I×U中条件(6)和(7)成立,并且假设存在一个C2-函数V(t,x)关于t是T周期的,且下列条件在某个紧集外成立:

(8)

LV(t,x)≤-1,

(9)

则方程(5)存在一个T周期解,即该解是一个T周期的Markov过程。

2 主要结果及其证明

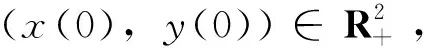
证明首先考虑如下方程

(10)

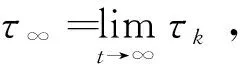
假设τ∞→∞成立，否则存在常数T>0、ε∈(0,1)和一个正整数k1≥k0,有P{τk≤T}≥ε,∀k≥k1。

LV=r(t)x-r(t)x2/K(t)-b(t)xy-r(t)+r(t)x/K(t)+b(t)y+λ(t)b(t)xy/(1+b(t)h(t)x)-

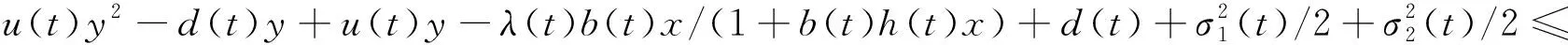
因此,V(x(τk∧T),y(τk∧T))≥(k-1-lnk)∧(1/k-1-ln 1/k)。则M≥E[1Ωt(θ)V(x(τk∧T),y(τk∧T))]≥ε([k-1-lnk]∧[1/k-1-ln 1/k]),其中1Ωt(θ)是在Ωk上的一个指示函数。令k→∞,则∞>M=∞。这与假设相矛盾,证毕。

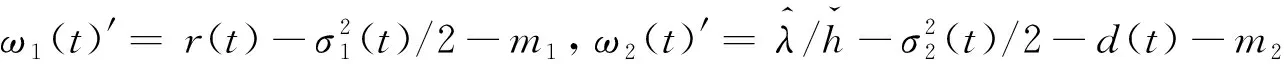
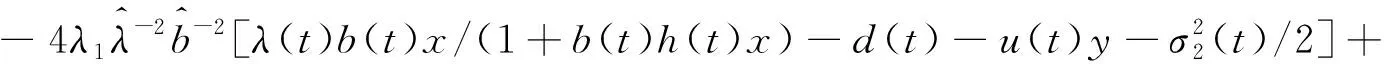
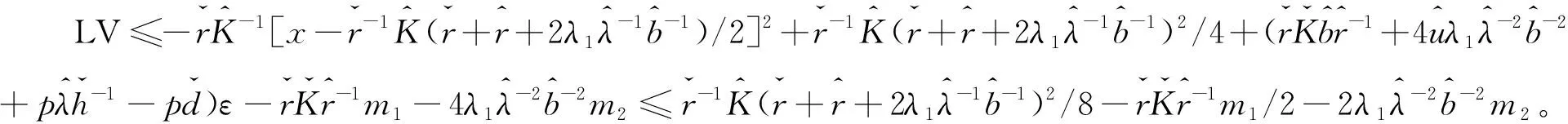
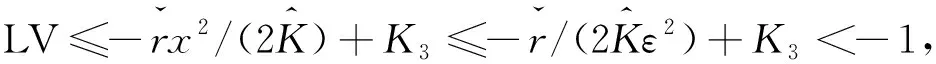
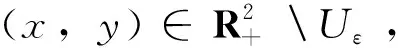
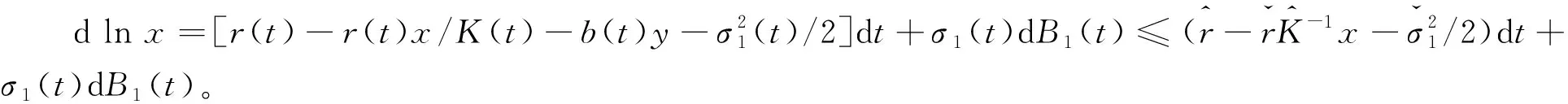
构造一个比较系统

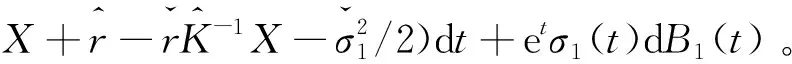
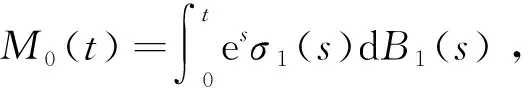
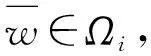
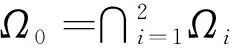
证明ⅰ)构造

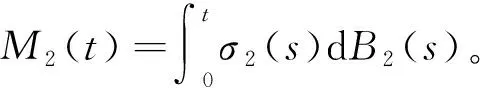
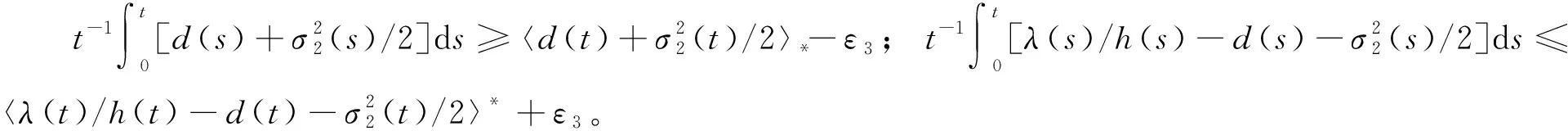
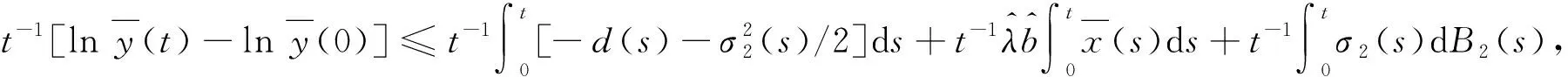
由系统(3)容易得到

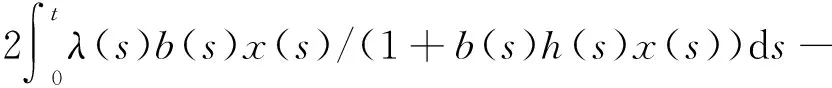
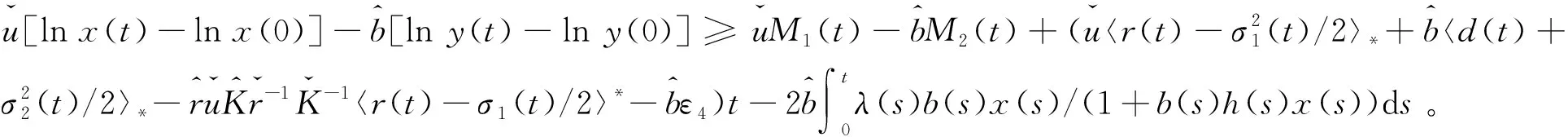
由系统(3)的第二个方程容易证得，

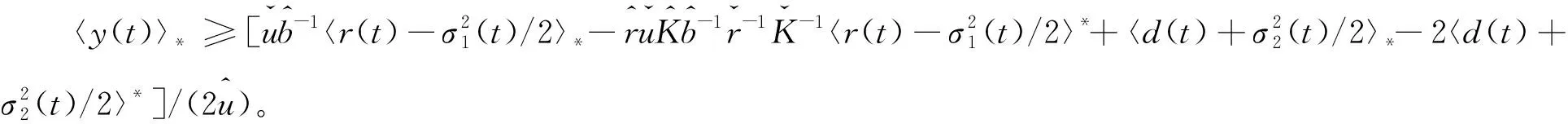
3 数值模拟

为了验证理论结果,采用Milstein高阶方法[18]对模型(3)进行数值模拟。

取初值(x(0),y(0))=(1.436,0.282),参数r=0.8+0.01sin(πt/5)，K=1.5+0.01sin(πt/5)，λ=1.6+0.01sin(πt/5)，b=0.12+0.01sin(πt/5)，h=2+0.1sin(πt/5),d=0.16+0.01sin(πt/5)，u=0.16+0.01sin(πt/5)，σ1=0.01+0.001sin(πt/5)，σ2=0.01+0.001sin(πt/5)。所有参数都是以T=10的周期函数,系统(3)及其确定性模型模拟如图1所示。

在其他参数保持不变的情况下,取σ1=0.000 1+0.000 01 sin(πt/5)，σ2=0.000 1+0.000 01 sin(πt/5)。通过计算得:

且

1.307 2>0。

故满足定理4的条件,系统(3)存在一个正周期解(如图2)。

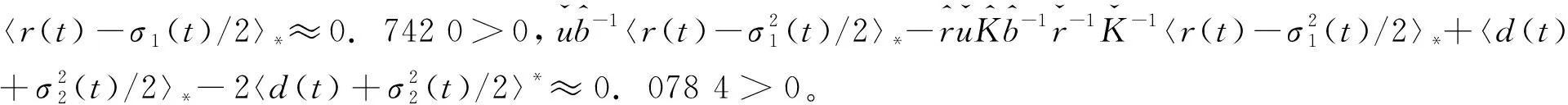
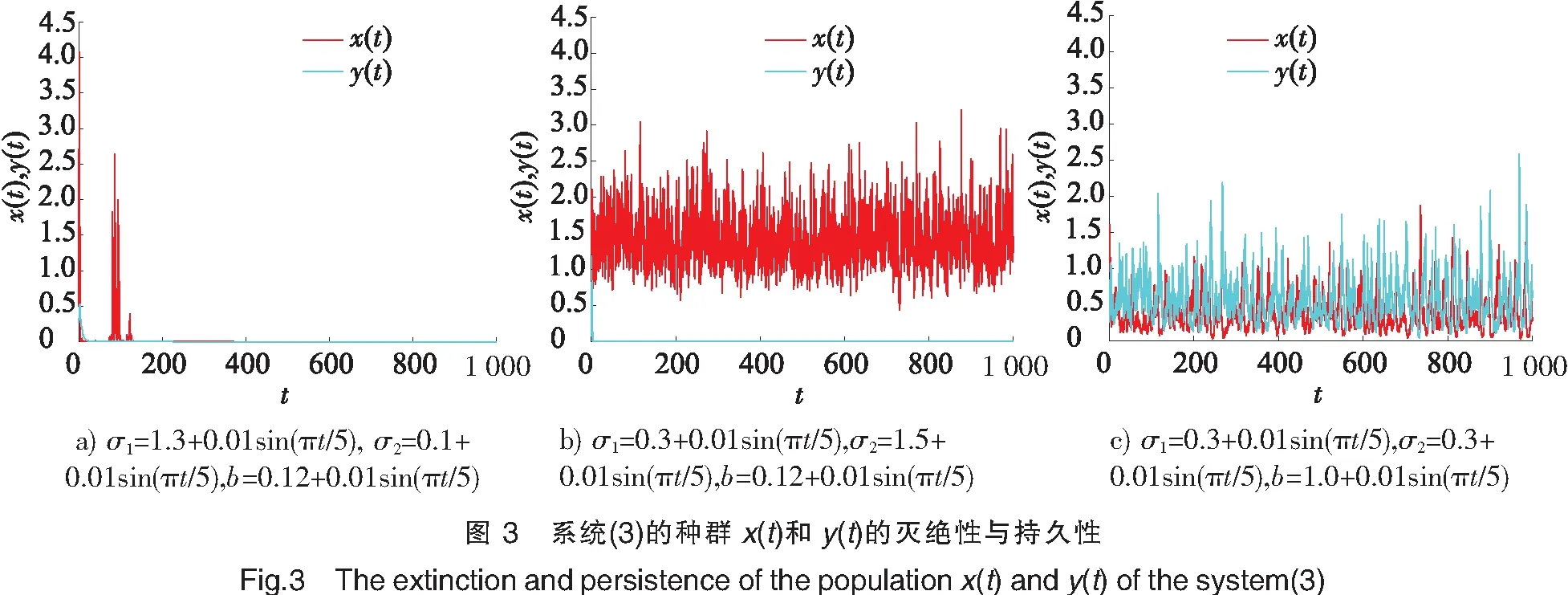
从生态学上看,白噪声的强度对种群x(t)和y(t)的生存具有负面作用。如果噪声强度足够小,种群可能持久;如果噪声强度足够大,则种群可能趋于灭绝。

4 结论