基于深度置信网络的车辆交通流预测

付永钢,李传目,王惠蓉

(1.集美大学计算机工程学院，福建 厦门 361021;2.集美大学海洋文化与法律学院，福建 厦门 361021)

0 引言

在智能交通系统(intelligent transportation system,ITS)研究领域，交通流的快速精确预测研究对智能交通有着重要的意义，是智能交通系统领域需要完成的主要任务之一[1-2]。快速和精确的交通流分析预测能准确规划和预测路径，对缓解道路拥堵具有重要的作用。此外，及时准确的交通流预测能有效为驾驶者提供后续的出行指导，使人们能够选择更好的出发时间和最佳的规划路线，避免交通堵塞。然而，交通流的预测受诸多因素的影响，难以在应用中进行实时预测。最近几年，随着智慧城市的逐步实施，在交通流预测方面做了大量的研究工作。到目前为止，现有的交通流预测方法大致可分为如下三类[3]：1)基于参数的方法；2)非参数的方法；3)混合方法。代表性的统计回归方法为自回归积分移动平均ARIMA(autoregressive integrated moving average)模型和ARMA(autoregressive moving average)模型[1]。ARIMA模型通常采用线性的移动平均回归的方法，该方法较大程度依赖于主观的参数设定，而交通网络又具复杂性和相互关联性，使得交通流预测的应用效果并不能令人满意。非参数回归方法是一种广泛应用的交通流预测技术[4]。通过前人的仿真研究结果[5-9]表明，基于非参数的交通流数据预测方法不能有效用于复杂条件下的模型建立和求解。为了有效处理复杂非线性交通状态下，对交通流时间序列进行非参数模型的有效分析和预测，一些研究人员提出了混合的方法[10-11]。在文献[12-13]中，多个参数模型被有效整合起来，可以实现对交通流进行分析和预测，但预测结果仍然存在较大误差。

深度学习已经吸引了众多研究者进行人工智能领域的研究和应用，尤其是在交通预测中[14-16]。文献[17]提出一种基于深度学习网络的交通流预测方法，通过设计一种简单的深度学习网络来学习交通流数据在一天中的前后关系，但预测精度有待提高。文献[18]采用多步RNN网络来进行训练和预测交通流，但总体预测精度仍然较大。文献[19]考虑了交通流数据的不完整性问题，参照了图像处理的CNN算法将交通流数据变换成图像的形状，采用CNN网络学习交通流数据中的时空关系，预测精度比SVR和ANN模型好。文献[20]使用深度学习架构，嵌入堆叠自动编解码器(stacked autoencoders,SAEs)作为主体网络结构块来预测交通流，在顶层添加了一个标准的预测器，提出了基于logistic回归的预测模型。很难说某种方法在任何情况下都明显优于其他方法，其中一个原因在于，所提出的模型都是基于少量单独的特定交通流数据而建立，而交通流预测方法的准确性依赖于所收集的时空交通数据中嵌入的交通流特征。同时，虽然神经网络的深层结构可以学习到比浅层网络更强大的模型，但现有的基于神经网络的交通流预测方法通常只有一个或几个隐含层，基于梯度的训练算法很难训练出层次较深的神经网络。深度置信网络(deep belief network,DBN)[21]是Hinton于2006年提出的一种快速训练的神经网络。目前基于DBN的交通流预测研究相对较少，鉴于DBN在机器学习领域的有效应用及其良好的性能，以及具有传统神经网络不能比拟的训练和预测优势，本文提出一种基于深度置信网络的交通流预测方法。

1 算法的提出

1.1 DBN算法

DBNs是由一系列受限玻尔兹曼机(restricted Boltzmann machines，RBMs)进行模块堆叠组成的概率生成模型，具体如图1所示。堆叠DBN时，通常由前一个RBM的输出层作为下一个RBM的可见层，依次进行堆叠，构成了基本的DBN结构，最后增加一个输出层，从而形成最终的DBN架构。

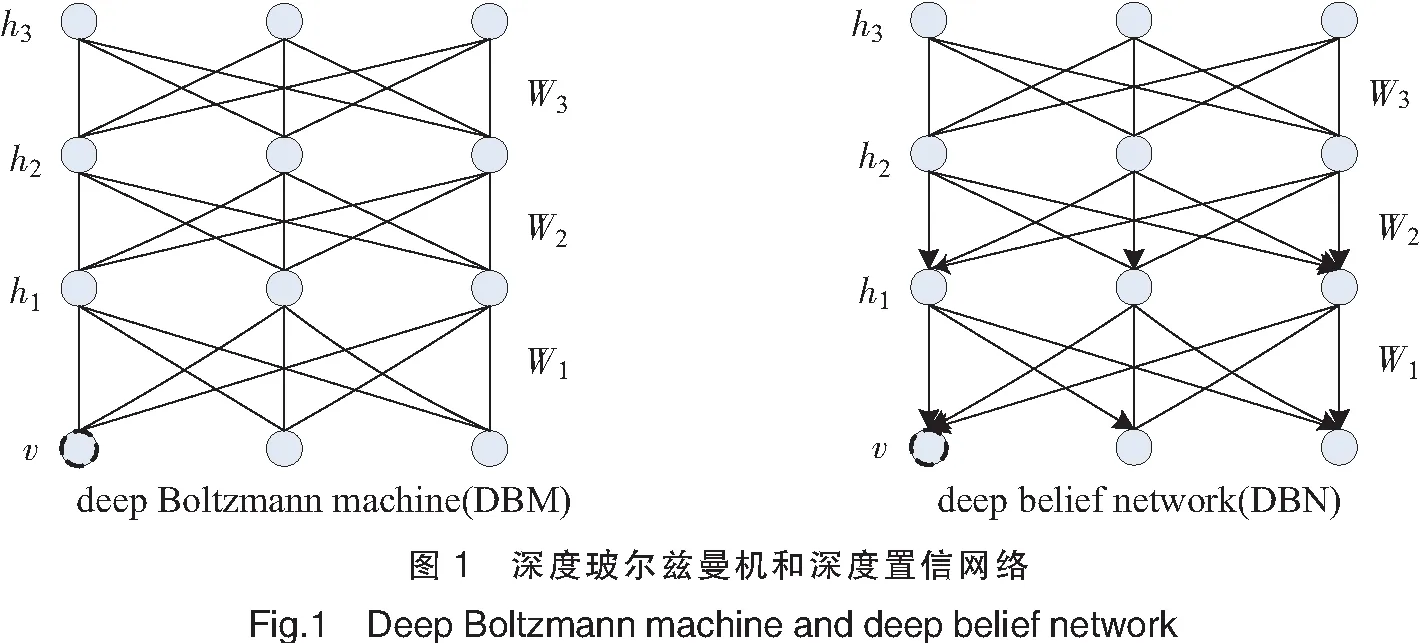
RBM是一种具有随机性的生成型神经网络结构，它本质上是一个无向图模型，由一层可见神经元和一层隐藏神经元组成，具有随机性。只有隐藏层和可见层的神经元之间有联系，而可见层和隐藏层的神经元之间没有连接。RBM的训练过程可以以贪婪的分层方式进行训练，并对从原始输入数据中提取的抽象层次特征进行权值微调；此外，还可以确定输入数据的条件概率分布，学习对变换具有鲁棒性和不变性的抽象特征。

在RBM中，当输入v时，利用P(h|v),可以计算出隐藏层h的概率，然后通过P(v|h),得到显示层v，通过参数的微调，使从隐藏层得到的显示层v1与原始显示层的v相同，如果隐藏层与原始显示层v相同，则隐藏层h是显示层的另一种表现形式。因此，隐藏层可以作为显示层输入数据的特征。

基于各层间能量偏差的相互作用和各层之间的相互作用，可以导出RBM的能量函数，具体能量函数可以定义为：

其中b和c分别是对应于隐藏层和显示层的偏移向量，是隐藏层和显示层之间的权重。所有这些参数包括b、c和w都可以统一用一个参数向量θ来表达。

根据该能量函数，本文给出每个可能的显示层和隐藏层的概率：

P(x,h)=e-E(x,h)/Z，

(1)

(2)

因为在隐藏层之间不存在连接，所以通过层间的关系很容易求出隐藏层的分布〈xihj〉data。给定随机选择的训练数据x、隐藏层j，可得：

近日，央行发布《2018年第三季度中国货币政策执行报告》（以下简称《报告》）。据了解，2018年第三季度以来，中国经济总体保持平稳增长，结构调整继续推进，供需总体平衡，经济运行韧性较强。消费对经济增长的拉动作用增强，制造业和民间投资增速回升，就业稳中向好，消费价格温和上涨。第三季度，国内生产总值（GDP）同比增长6．5%，居民消费价格（CPI）同比上涨2．3%。但需要注意的是，受外部环境发生明显变化及需求端“几碰头”等因素影响，目前经济下行压力有所加大。

(3)

其中σ(x) 是sigmoid函数。同时也注意到，在可见层之间也是没有连接的，因此可以计算出概率分布：

(4)

如果增加隐藏层的数量，则会得到DBM(deep Boltzmann machine);如果采用有向图模型BBN(bayesian belief network)在层内节点间无连接，并且在可见层的远端采用RBM，则会得到新DBN[22-23]。

1.2 算法框架

本文提出的基于DBN的交通流预测模型框架如图2所示， 具体算法描述如下：

步骤1) 交通流数据预处理。由于传感器的失误等原因的存在，收集到的数据中通常会有一些异常数据和丢失的数据。数据预处理需要对这些异常数据进行分析整理，剔除异常数据;并对缺失数据进行补全。通常补全数据的方法有很多，比如常用的有均值替换、KNN替换[24]、MissForest[25]、EM算法[26]、MODE算法[27],等等。通过比较，用均值替换方法进行数据缺失处理具有效率上和性能上的优势，因此，本文采用均值替换方法来补足缺失数据。由于交通流的数据量通常很大，大绝对值的数据对交通流的预测具有很大的影响。为了消除交通流数据绝对值对预测结果的影响，在进行分析之前，需要对数据做归一化处理，本研究采用了min-max归一化方法:

x′=(x-min(x))/(max(x)-min(x))，

(5)

x=x′×(max(x)-min(x))+min(x)。

(6)

其中:x是待归一化的数据；x′是归一化以后的数据。

步骤2) 结构化数据。先对给定的交通流数据同时间等相关数据进行分割组合，形成待预测的特征向量；再对这些特征向量进行拆分，形成训练数据集和测试数据集；最后把这些数据进行重组，形成结构化的训练数据，作为交通流的预测数据集。

步骤4) 进一步调优网络预训练结果。调优的过程采用的是有监督的训练过程，即对每条记录都有训练标号。这个过程需要首先利用前向传播算法，从输入得到对应的输出值，然后利用反向传播算法来更新网络权重和偏移量。

步骤5) 在预测部分，采用了经典的单层BP(back propagation)网络结构来进行交通流的预测，根据训练好的网络，对测试数据集进行预测，给出预测的数据结果。

2 结果与分析

本研究对提出的方法在实际应用的数据集上进行验证和分析。首先，给出后续需要用到的数据集以及相关的一些指标定义；然后，给出实验结果，每个实验结果都是在10次实验的基础上，再加5次交叉验证；最后，给出同相关研究算法进行比较的结果。

2.1 数据集及评价指标

为了评价本方法的有效性，本研究采用了美国Caltrans Performance Measurements Systems(PeMS)[29]数据集，该数据集在网上可以公开获取。Caltrans PeMS在高速路上放置了39 000多个独立探测器，这些探测器分布在加州城市区域的多条道路上，可以实时获取相关时间、车速、车流等多种数据，因而该数据被广泛用作智能交通领域的benchmark数据集。该数据集采集的是以5 min作为间隔的各类数据。本文从该数据集中获取2016年1月4日到3月31日共3个月的交通流数据，其中包含153个车辆监测点数据。

本研究对数据做了简单的异常剔除，并对缺失数据采用Mean缺失修复方法做了补足处理，这样可认为获取的数据都是正常数据。对获取的数据在相同条件下用不同模型进行训练和分析，并给出对比结果。在以往的算法模型中，通常会区分工作日和非工作日的车流，因为在工作日的车流数据同非工作日有明显的差异；但在本文中，没有单独区分工作日车流和非工作日车流，因为实际上非工作日车流在整个数据集中所占比例偏小，并不会对整个数据的预测起到重要的影响，且从实验结果来看，与区分工作日车流和非工作日车流进行预测的结果并没有明显的差异。在整个数据集中，总计约有12 097条记录，这个数据集在训练和预测过程中被主观按照7∶3的比例分为训练集和测试集，且这两个集合之间没有交叉数据，通过测试集数据检验了训练结果的有效性。

在整个训练和测试过程中，本研究采用了均方根误差(root mean square error，RMSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)、均方误差(mean square error,MSE)、平均绝对误差(mean absolute error,MAE)和R2检验指标来评价。设targeti,j是预测(i,j)位置的目标数据点，predi,j是该位置的预测数据值，D是所有待预测数据位置集合，N是总的数据数，则这些指标的定义如下：

(7)

作为时序数据的预测和分析，LSTM、GRU和SAEs这三种模型被认为是最好的时序数据处理的网络模型。将本文算法同这三种预测模型进行了预测结果的比较。

本文提出的预测分析模型在PyTorch平台架构上实现，用于对比实验的LSTM、GRU和SAEs的模型编程从Github公开渠道获得，它们都是采用PyTorch进行编程实现。本文的训练和测试结果都是采用了5次交叉有效性验证获得的。

2.2 实现结果

在本实验中，DBN预测模型基于PyTorch框架实现，采用了两个隐层，对应的隐层参数分别为128和64，预训练和调优参数分别为500和2000。在对比的LSTM、GRU预测算法中，采用了三层隐藏层数，分别为12、64、64的LSTM、GRU单元。SAEs算法采用了三层自编码器的结构，对应每层隐藏单元数分别为400、400、400，再分别叠加起来。在所有对比的算法中，对应的损失函数均采用了均方误差函数，优化函数为Adam优化器,并叠加了参数为0.2的Dropout。

图3展示了用本算法预测的从2016-03-08T09:30开始的24 h内整个数据集的结果，可以看出其能够较好地预测实际的交通流数据。

图4展示了本文提出的训练预测模型同LSTM、GRU和SAEs[5]三种模型在相同时间段内的预测结果。从图4可以看出：基于LSTM和GRU的模型在开始的时间段内预测误差相对较大；在21:00—5:00这段时间内所有模型的预测性能误差均比较小；在7:00—9:00时间段内SAEs的预测误差较大，GRU的预测误差也有点偏大。

表1显示了在该数据集上进行训练以后，在测试集上进行预测，得到的对应评价指标值(MSE、MAE、MAPE、R2和RMSE)。从表1可以看出，本文提出的基于DBN的预测模型在各种性能指标下都具有最优值。GRU模型的MSE、MAE、RMSE的值最大，而SAEs模型的MAPE值最大。R2作为回归模型的一个重要评价指标，通常最好的模型应该接近1，而该值越小则意味着该模型效果越差。 在这几个评价指标中，GRU模型的R2指标最小为0.9338，而DBN模型得到的R2为0.9690。

表1 不同模型的比较结果

综合来看，本文提出的DBN模型能够较好地预测该交通流数据，同LSTM、GRU和SAE模型相比，在预测精度上优势明显。

3 结论

本文提出一种基于DBN的神经网络模型，用来训练和预测交通流数据。从实验结果来看，本模型同现有的LSTM、GRU和SAEs模型相比，具有较好的预测性能：更小的误差，同时R2指标具有最佳值。这主要源于DBN模型出色的特征提取能力和良好的学习能力，因此该模型具有更好的泛化推广能力。