脉间-脉内捷变频雷达抗间歇采样干扰方法

刘智星 杜思予 吴耀君 沙明辉 邢孟道 全英汇*

①(西安电子科技大学电子工程学院 西安 710071)

②(北京无线电测量研究所 北京 100854)

③(西安电子科技大学前沿交叉研究院 西安 710071)

1 引言

随着电子技术的发展，数字射频存储 (Digital Radio Frequency Memory,DRFM) 技术在干扰机中得到了广泛的应用，其中，以间歇采样转发式干扰最具代表。间歇采样转发式干扰可以在一个脉冲内对雷达信号进行多次采样和转发，利用脉压雷达的匹配滤波特性，形成逼真的相参假目标串[1]，以掩护真实目标。

对于间歇采样转发式干扰，诸如脉间频率捷变[2,3]、波形捷变[4]等技术已无法有效对抗，对雷达造成了严重的威胁，引起了国内外学者的广泛关注。从奇异值分解和信息熵理论出发，文献[5]提出了一种基于奇异谱熵函数的间歇采样干扰抑制方法，对回波奇异谱进行熵检测，通过带通滤波实现干扰抑制，该方法可提高脉压后的目标检测概率和峰值旁瓣比。针对改进的间歇采样转发干扰，文献[6]通过给雷达发射信号增加一个频移使抵消信号与目标回波同相，进而使真实目标功率高于虚假目标功率，区分出目标与干扰，但该方法并没有抑制掉所有假目标。Wei等人[7]利用时频分析方法对干扰参数进行提取，然后设计脉内频率编码波形，通过时域带通滤波器在脉压的输出滤除假目标。此外，文献[8–10]也采用时频分析的方法构造带通滤波器来对抗间歇采样干扰。文献[11,12]均采用优化方法对雷达信号进行优化，并利用雷达信号与干扰信号的正交性在匹配滤波时抑制干扰信号。Zhou等人[13]基于重构和对消的思想，利用时频域信息和反卷积处理估计出的参数重构出干扰信号，并通过迭代对消实现干扰抑制。文献[14]通过在时域提取未被干扰的信号，建立稀疏目标模型，利用贝叶斯压缩感知对信号进行稀疏重构，该方法在干扰占空比较高的情况下，性能将有所下降。文献[15]根据目标信号与干扰信号在统计域的差异，构造了频移滤波器对间歇采样干扰形成的假目标进行抑制。此外，张建中等人[16–18]针对间歇采样转发干扰的抑制进行了深入的研究，利用分段信号之间的正交性，通过窄带滤波器组对干扰和目标进行分选，剔除干扰[16]。文献[18]则采用脉内频率步进的线性调频(Linear Frequency Modulation,LFM) 信号，利用短时傅里叶变换在时频域进行干扰抑制，再通过逆变换恢复出时域信号，最后利用分段脉压实现脉内积累。万鹏程等人[19]提出了一种基于分数阶傅里叶变换 (Fractional Fourier Transform,FrFT) 的干扰抑制方法，但目标与干扰在分数阶傅里叶域混叠，高干信比下重构信号包含大量干扰分量。在脉间频率捷变的基础之上，文献[20]提出了一种脉间频率捷变联合脉内频率编码的雷达波形，采用最大类间方差法 (Otsu) 自适应计算阈值剔除被干扰的子脉冲，但该方法脉内积累后存在较大的幅度损失，降低了雷达的检测性能。

本文根据间歇采样干扰的特点，在文献[19]的基础上，结合脉间-脉内捷变波形的“主动”抗干扰优势，利用脉内频率捷变提高雷达信号与干扰信号的区分度，提出了一种基于分数阶傅里叶变换的并行干扰抑制算法。首先，在时域对干扰进行提取并切片处理，然后在分数阶傅里叶域通过窄带滤波器提取目标信号，并进行分数阶傅里叶逆变换恢复出时域信号，最后利用分段脉压完成脉内积累。仿真实验表明，该方法在脉内积累后幅度损失较小，不会引起很高的干扰旁瓣且适用于较高干信比的情况。

2 间歇采样转发干扰

基于DRFM技术的干扰机能够在一个脉冲内精准、迅速地复制雷达发射波形，并快速转发形成与目标类似的干扰信号，在时域、频域覆盖真实目标，严重影响了目标的检测与跟踪。如图1所示，根据采样宽度、采样次数的不同，间歇采样转发干扰主要可以分为间歇采样直接转发干扰 (ISRJDF) 和间歇采样重复转发干扰(ISRJ-RF)两种基本样式。

假设干扰机截获到第n个发射脉冲信号x(t,n)，直接转发干扰的采样信号为r(t)，则间歇采样直接转发干扰信号可以表示为

其中，Aj表示干扰信号幅值，⊗表示卷积运算，τc和Tj分别为干扰机采样时延和干扰机采样宽度，Q=Tp/Tq表示当前脉冲内间歇采样直接转发干扰的采样次数，Tp表示雷达脉冲宽度，Tq表示间歇采样干扰重复周期。

如图1(b)所示，与间歇采样直接转发干扰不同，对于间歇采样重复转发干扰，当干扰机对截获的雷达信号进行采样后，会按照设定的转发次数不间断地重复转发。假设重复转发次数为K，重复转发干扰的采样信号为r′(t)，则间歇采样重复转发干扰可以表示为

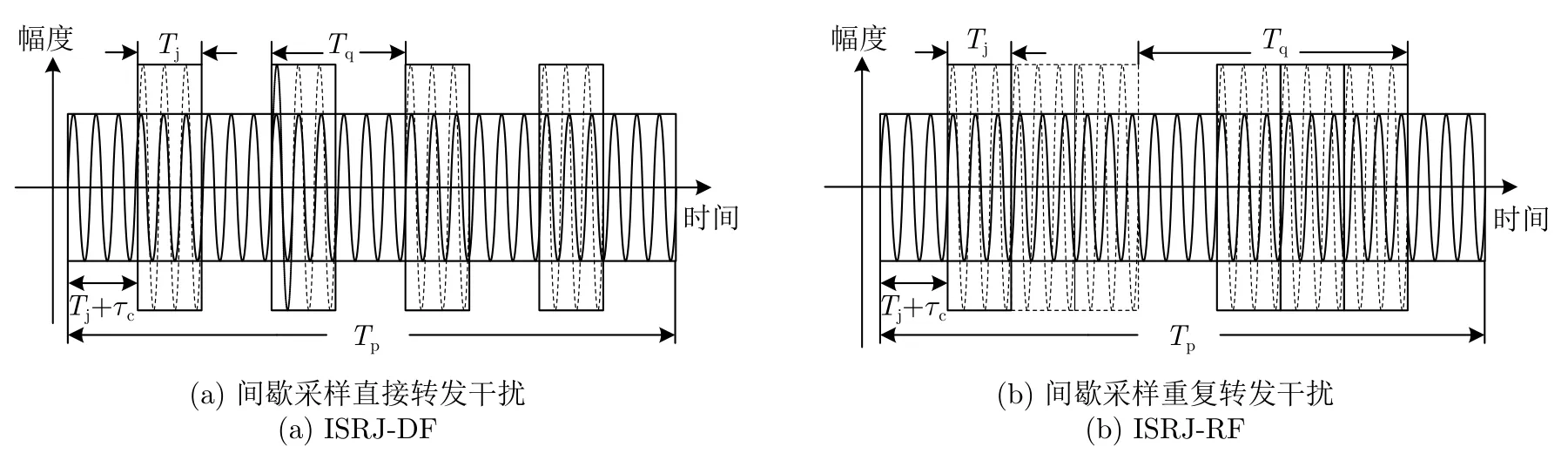
图1 间歇采样转发干扰示意图Fig.1 Schematic diagram of ISRJ

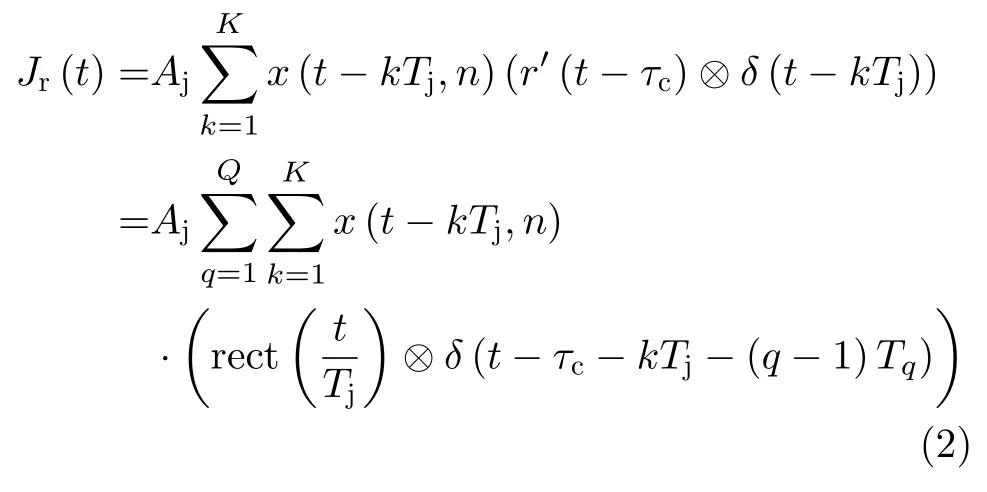
其中，K=⎿Tq/Tj」−1。当重复转发次数K=1时，式(2)与式(1)相同，即间歇采样直接转发干扰可以认为是间歇采样重复转发干扰的特例。

在间歇采样干扰场景下，雷达接收到的第n个脉冲回波信号s(t,n)可以表示为

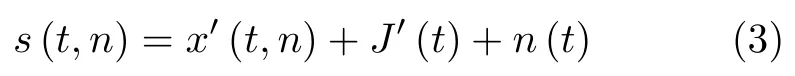
其中，x′(t,n)为第n个脉冲对应的目标回波，J′(t)表示雷达接收到的间歇采样转发干扰，n(t)为加性高斯白噪声。

3 脉间-脉内捷变频雷达信号模型

脉间频率捷变雷达能够“主动”规避干扰覆盖频段，难以被侦察机截获，因此能够有效对抗窄带瞄准式干扰和距离前拖式干扰等[21]。然而，间歇采样转发式干扰能够在脉冲内对雷达信号进行多次采样和转发，使得脉间频率捷变抗干扰方法失效。通过对2.2节间歇采样干扰生成机理分析可知，干扰具有时域不连续的特点。利用这一特点，基于子脉冲交替掩护思想，本文采用脉间-脉内频率捷变波形来对抗间歇采样转发干扰。

如图2所示，假设雷达发射N个脉冲，脉宽为Tp，带宽为B，每个脉冲包含M个子脉冲，子脉冲宽度为Ts=Tp/M，子脉冲带宽为Bs=B/M，每个子脉冲的波形调制为线性调频，则第n个脉冲内的第m个子脉冲可以表示为

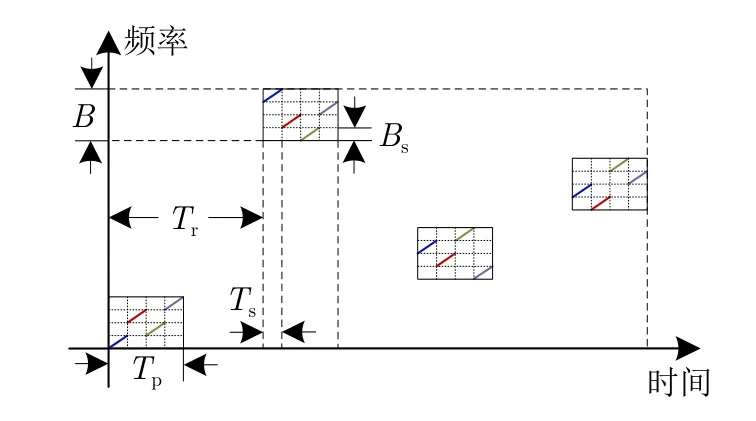
图2 脉间-脉内捷变频波形时频图Fig.2 Time-frequency diagram of inter-and-intra-pulse frequency agile waveform

其中，Tr为脉冲重复周期。

假设雷达观测场景中共有I个运动目标，第i个目标初始径向距离为Ri，径向速度为vi，则第n个脉冲回波的时延表示为τn,i=2(Ri −vi(n −1)·Tr)/c,c表示光速。雷达接收到的目标回波信号可以表示为

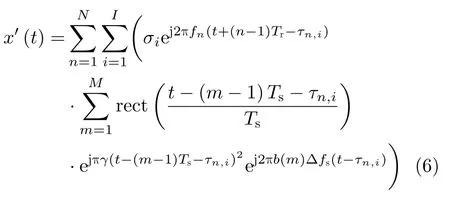
其中，σi表示第i个目标的散射系数。

4 脉间-脉内频率捷变必要性分析

当场景中存在单个点目标，雷达发射信号采用脉间-脉内捷变频波形，干扰机以子脉冲宽度Ts为采样时长对雷达发射信号进行同步采样，以间歇采样直接转发干扰为例，对第n个脉冲回波进行分析，则式(3)可以简化表示为

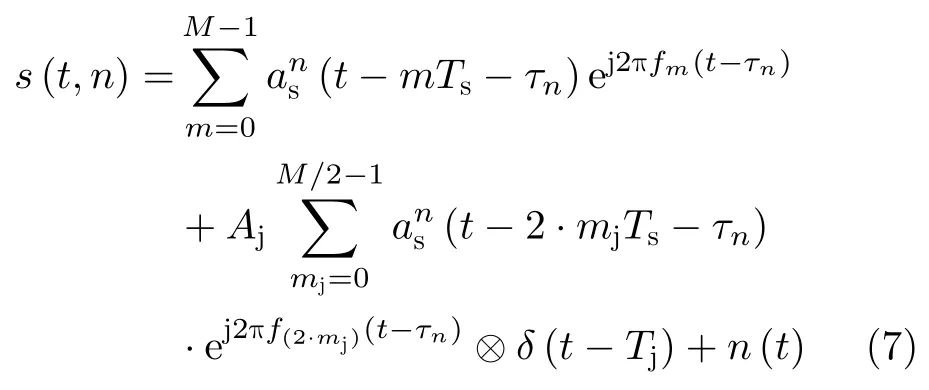
对于LFM信号，间歇采样转发干扰的时频分布如图3所示。可以看出，由于干扰幅度通常远大于目标幅度，干扰信号经短时傅里叶变换 (Short-Time Fourier Transform,STFT) 后会呈现出一条“亮带”，干扰信号在频率维存在较高旁瓣，使得目标信号与干扰旁瓣混叠，这给间歇采样干扰的抑制带来很大困难。如图4所示，当采用脉间-脉内捷变频信号时，由于脉内频率随机跳变，提升了干扰信号与目标信号在时频域上的区分度，避免了干扰旁瓣对目标信号的影响，为后续的抗干扰处理提供了便利。其次，随机跳频使得相邻频带脉压后的干扰残余项在距离维均匀分布，无法实现积累，从而避免了干扰带的形成[17]。

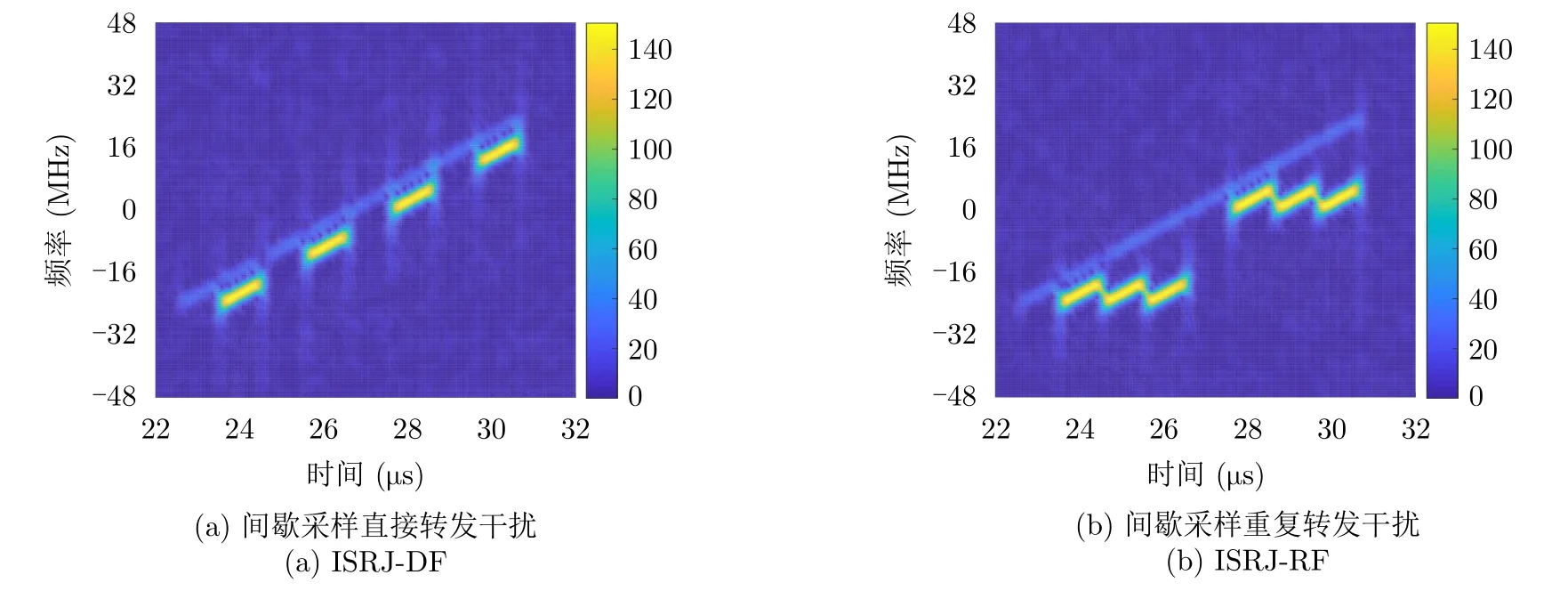
图3 LFM回波信号时频图Fig.3 Time-frequency diagram of LFM echo signal

图4 脉内捷变频回波信号时频图Fig.4 Time-frequency diagram of intra-pulse frequency agile echo signal

值得注意的是，为了保证脉间-脉内捷变频波形与间歇采样转发干扰的“匹配”，需要考虑间歇采样干扰的类型、采样宽度以及采样周期等参数，使子脉冲宽度和间歇采样干扰的采样宽度相同，同时尽可能增强干扰与目标信号之间的区分度。因此，在波形设计时，需要预先感知干扰，即对场景中的间歇采样干扰的参数进行估计，本文假设干扰参数已知。

基于上述分析可知，脉间-脉内捷变频波形可以显著降低干扰对目标信号的影响，但无法完全抑制干扰信号，因此，在波形设计的基础上，还需要对回波信号采取一定的抗干扰措施。从图4可以看出，通过设置阈值滤除“亮带”能够实现干扰抑制，但直接在时频域上将干扰剔除仍会保留与目标幅度相近的大量干扰信号旁瓣，严重影响后续目标检测。综合以上两个问题，结合脉间-脉内捷变频信号特点，针对典型的间歇采样干扰样式(间歇采样重复转发、间歇采样直接转发以及两种不同的间歇采样转发干扰样式组成的复合干扰)，本文提出了一种基于FrFT的间歇采样转发干扰抑制方法。

5 基于FrFT的间歇采样转发干扰抑制方法

5.1 分数阶域干扰抑制

分数阶傅里叶变换是一种广义的傅里叶变换方法[22]，表示为

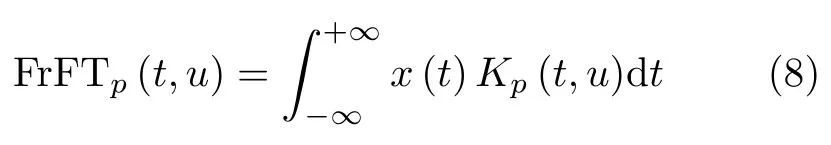
其中，p为FrFT阶数，旋转角度φ=pπ/2,Kp(t,u)为FrFT的变换核函数

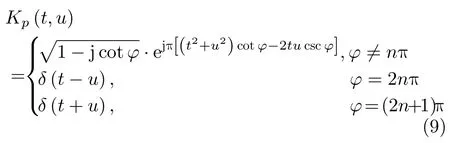
如图5所示，由于FrFT可以直观地理解为时频面以角度φ围绕原点逆时针旋转，随着旋转角φ的变化，LFM信号在分数阶域的频谱具有不同的聚集特性，且当旋转角度为φopt时，LFM信号在该“最佳”分数阶域出现谱峰。

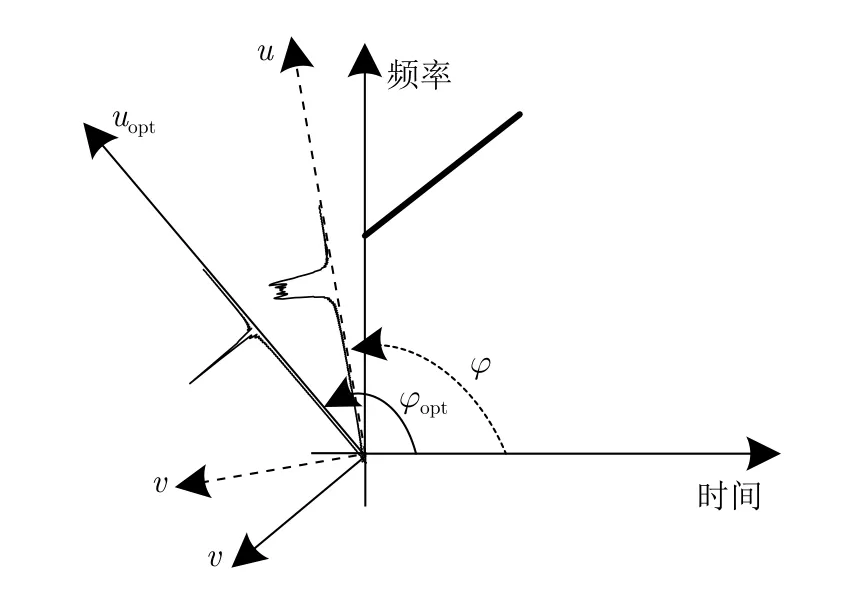
图5 LFM信号分数阶傅里叶域频谱特征Fig.5 Spectral characteristics in fractional Fourier domain of LFM signal

因此，本文综合考虑子脉冲频率捷变特点、间歇采样转发式干扰非连续特性以及LFM信号分数阶傅里叶域频谱聚集特征，提出了一种基于FrFT的间歇采样转发干扰抑制方法。如图6所示，在干扰抑制时，首先对被干扰的信号段进行提取，并以子脉冲宽度为单元对其进行切片，分散干扰能量的同时，使每个切片中尽可能只保留一个完整的子脉冲，以便后续干扰抑制处理。具体算法步骤如下：

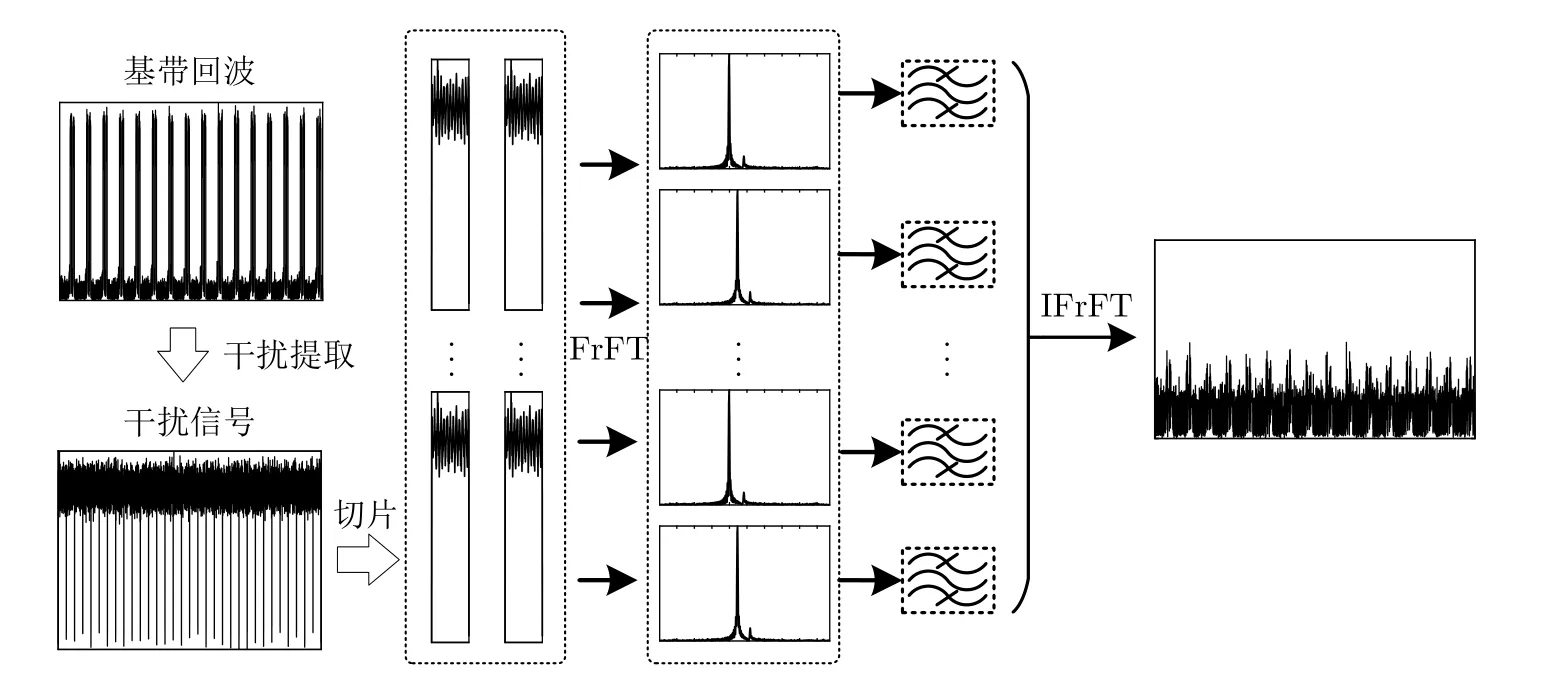
图6 分数阶傅里叶域并行干扰抑制流程图Fig.6 Flow chart of parallel interference suppression in fractional Fourier domain

步骤1 雷达接收到的第n个脉冲回波s(t,n)，对其进行下变频处理，得到基带回波信号，并在时域上提取被干扰的信号段sj(t)；

步骤2 以子脉冲脉宽Ts为单元，对sj(t)进行切片，得到G=⎿TG/Ts」个子段，其中，TG为被干扰信号段的总时宽，第g个切片时域表示为

步骤3 对切片所得的G个被干扰信号子段并行做FrFT，将时域数据变换到分数阶傅里叶域，其中第g个切片在分数阶域的表达式为[22]

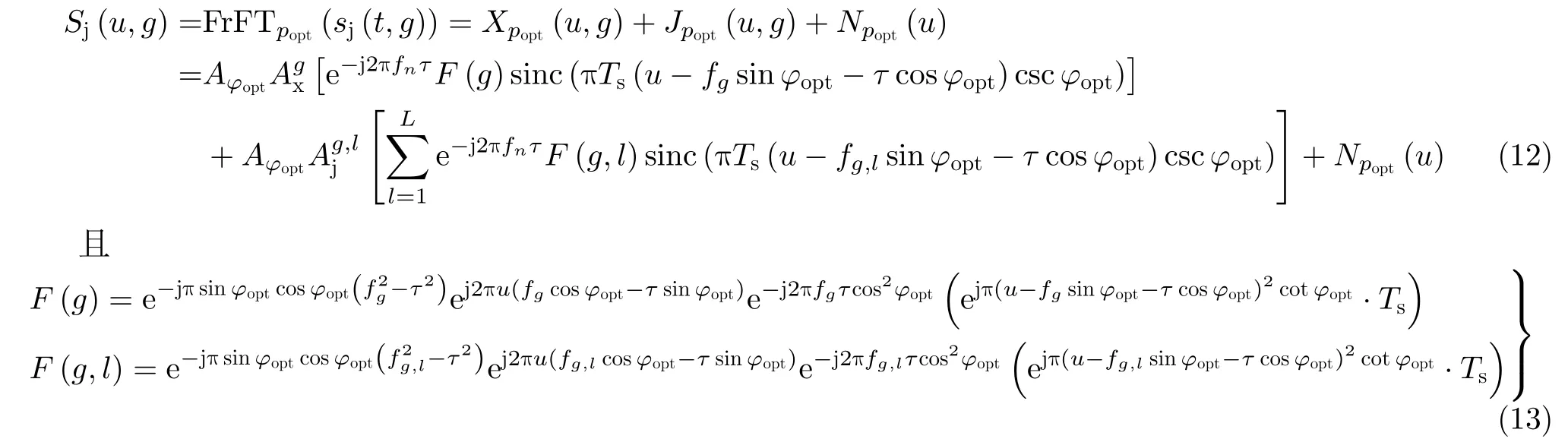
由式(12)可以看出LFM信号在“最佳”分数阶傅里叶域的频谱服从sinc函数分布。其中，分别对应第g个切片中目标回波分量、干扰分量和噪声分量的FrFT域变换形式；和分别表示第g个切片的目标幅度和第g个切片中第l个干扰的幅度；popt为FrFT最佳变换阶数，最佳旋转角度φopt=poptπ/2,fg=b(g)∆fs表示第g个切片中子脉冲的中心载频，fg,l=b(g,l)∆fs表示第g个切片中第l个干扰信号的中心载频。

步骤4 第g个子段FrFT中，sinc函数峰值点分别表示目标信号和干扰信号，对应分数阶傅里叶域位置分别为fgsinφopt+τcosφopt和fg,lsinφopt+τcosφopt，构造窄带滤波器组，对G个被干扰信号子段在分数阶傅里叶域进行滤波，保留目标回波，同时抑制干扰信号。

步骤5 将步骤4中滤波后的结果经IFrFT变换到时域，得到干扰抑制后的脉冲信号

5.2 分段脉压

由于本文采用的雷达发射信号为脉间-脉内频率捷变LFM信号，无法直接用一个匹配滤波器进行脉冲压缩。因此，本文通过构造M个子匹配滤波器来完成脉压处理。

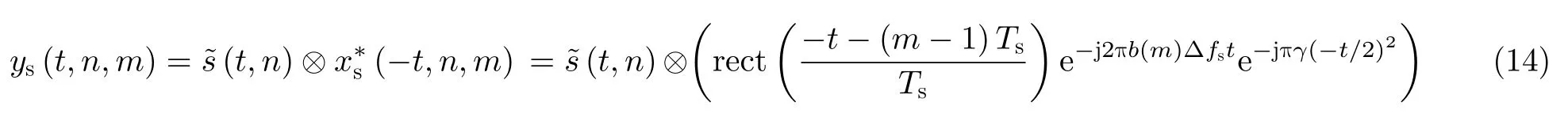
接下来对所有子脉冲进行脉内积累，则雷达回波经分段脉压后可以表示为

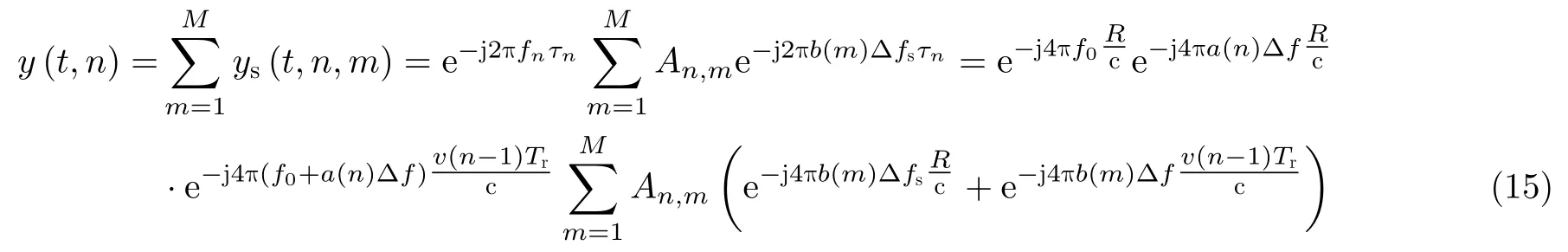
综上所述，本文将脉内频率捷变波形设计与切片式FrFT干扰抑制算法结合，首先利用脉内频率捷变提升目标与干扰在分数阶傅里叶域的区分度，便于干扰信号的识别与剔除；然后在分数阶域对被干扰的子脉冲利用窄带滤波提取目标回波，进而实现对干扰的抑制。由式(15)可以看出，在分段脉压过程中，所有的子脉冲都得到了积累，因此脉压损失较小，而文献[16,17,20]均在分段脉压过程中将被干扰的子段剔除。这种方式虽然能够抑制干扰，但在回波信号处理时会失去此部分的信号增益，导致信噪比降低，同时频带缺失会引入栅瓣，当被干扰子脉冲较多时，增益损失增加，栅瓣较高，脉冲压缩效果不理想，影响后续相参检测处理。

6 仿真实验

为验证本文所提方法的抗干扰性能，共设计2组仿真实验，采用MATLAB软件分别对间歇采样直接转发干扰、间歇采样重复转发干扰和多主瓣干扰进行仿真分析。雷达工作在Ku波段，脉内波形调制为线性调频，具体波形参数如表1所示。

表1 雷达波形参数设置Tab.1 Radar waveform parameter setting

6.1 仿真实验1

针对间歇采样直接转发干扰，假设场景中目标径向距离R=4100 m，径向速度v=32 m/s，干扰机与目标在同一距离，干扰采样宽度Tj=1 µs，采样周期Tq=4 µs，目标信噪比(Signal to Noise Ratio,SNR) 为 0 dB，信干比(Signal to Interference Ratio,SIR) 为–20 dB。从图7(a)可以看出，子脉冲2和子脉冲4存在干扰。采用本文所提方法对干扰进行抑制，如图7(b)所示，所提方法可以有效地抑制间歇采样直接转发干扰。图7(c)为采用本文所提方法和无干扰情况下脉压输出结果对比。图7(d)为分别采用本文所提方法、文献[20]所提干扰抑制方法以及文献[18]的时频域干扰抑制方法的脉压输出结果。可以看出，3种干扰抑制方法均能有效对抗间歇采样直接转发干扰。由于时频域干扰抑制后仍存在少量干扰残余，文献[18]的方法脉压后的旁瓣高于本文所提方法。而文献[20]是将被干扰的子脉冲直接剔除，其脉压输出后幅度损失较大。而本文所提方法是在分数阶傅里叶域通过窄带滤波分离目标和干扰信号，尽可能只保留目标信号。因此，干扰抑制后的脉压结果与无干扰情况下雷达脉压结果基本一致，幅度损失较小，且干扰残余较少，旁瓣较低。

针对间歇采样重复转发干扰，设置干扰采样宽度Tj=1 µs，采样周期Tq=4 µs，重复转发3次，其他参数设置同上。仿真结果如图8所示，从图8(a)和图8(b)可以看出，子脉冲2～4均存在与子脉冲1相同的干扰，采用本文所提方法，子脉冲2～4的干扰被抑制。从图8(c)和图8(d)可以看出，与文献[18]和文献[20]相比，本文所提方法可以有效对抗间歇采样重复转发干扰，且脉压后幅度损失较小，旁瓣较低。

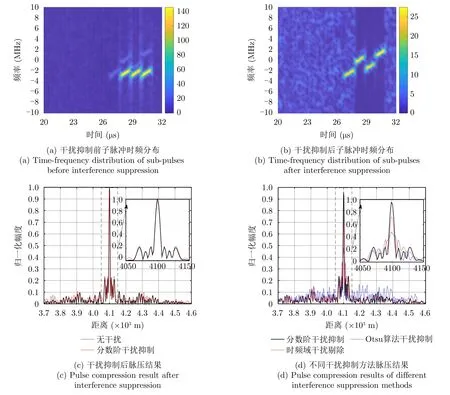
图8 间歇采样重复转发式干扰抑制结果Fig.8 ISRJ-RF suppression results

6.2 仿真实验2

针对两个主瓣干扰场景，假设雷达观测场景中存在两台干扰机(分别采用间歇采样直接转发干扰和间歇采样重复转发干扰)，参数设置与实验1相同。图9显示了脉间-脉内捷变频雷达在两个主瓣干扰条件下，经过抗干扰处理后的结果。从图9(a)可以看出，在多主瓣干扰下，子脉冲与干扰信号依然具有可分性。图9(c)为经过本文所提方法进行干扰抑制后的分段脉压输出，图9(d)为采取不同方法干扰抑制后的分段脉压输出；从图中可以看出，在多主瓣干扰下，干扰信号叠加，在频率维的旁瓣抬高，直接在时频域进行干扰剔除后，分段脉压输出的旁瓣严重影响目标检测；由于多种转发干扰叠加，一个脉冲内能够用于检测的未被干扰的子脉冲数减少，采用文献[20]所提Otsu算法进行干扰抑制后脉压输出幅度损失较大，对目标检测产生影响。对比图9(c)和图9(d)，本文所提方法能够有效对抗两个主瓣干扰，降低了脉压输出的干扰旁瓣所带来的影响，同时，保留了所有子脉冲回波的目标信息，减少了脉压输出的幅度损失。

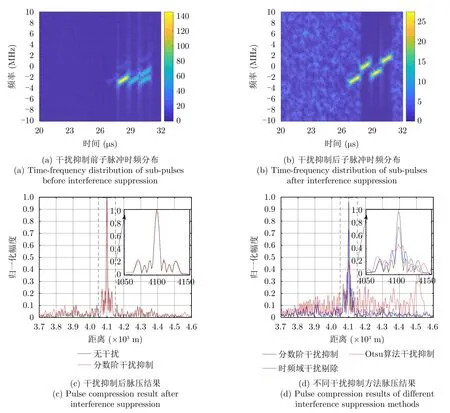
图9 仿真实验2结果Fig.9 Simulation 2 results

6.3 性能分析

本节针对影响所提算法性能的因素进行分析，包括干扰机非同步采样延迟τc对分段脉压积累增益损失的影响、子脉冲个数M对分段脉压栅瓣的影响以及信干比对干扰抑制算法性能的影响。

上述2组仿真实验均假设干扰机对雷达发射信号同步采样，即干扰机的采样延迟τc=0，针对干扰机非同步采样情况，对所提干扰抑制算法性能进行仿真分析。假设干扰机采用间歇采样直接转发式干扰，采样延迟τc服从(0,Ts/2]上均匀分布，其他参数设置同仿真实验1。图10(a)为τc=0.2 µs时，在分数阶傅里叶域对干扰进行抑制后的脉压结果，图10(b)表示经过100次独立的蒙特卡罗仿真实验，干扰抑制处理后的脉压幅值随采样延迟τc的变化曲线，其中采样延迟τc以0.05 µs为间隔在区间(0,Ts/2]上步进。

从图10(a)可以看出，当干扰信号与雷达信号不同步时，在不增加子脉冲数的前提下，本文所提算法依然能够有效抑制干扰。图10(b)显示出随着采样延迟τc增大，干扰抑制后脉压增益有所下降，当采样延迟τc等于子脉冲一半脉宽时，脉压增益下降约2.8 dB。

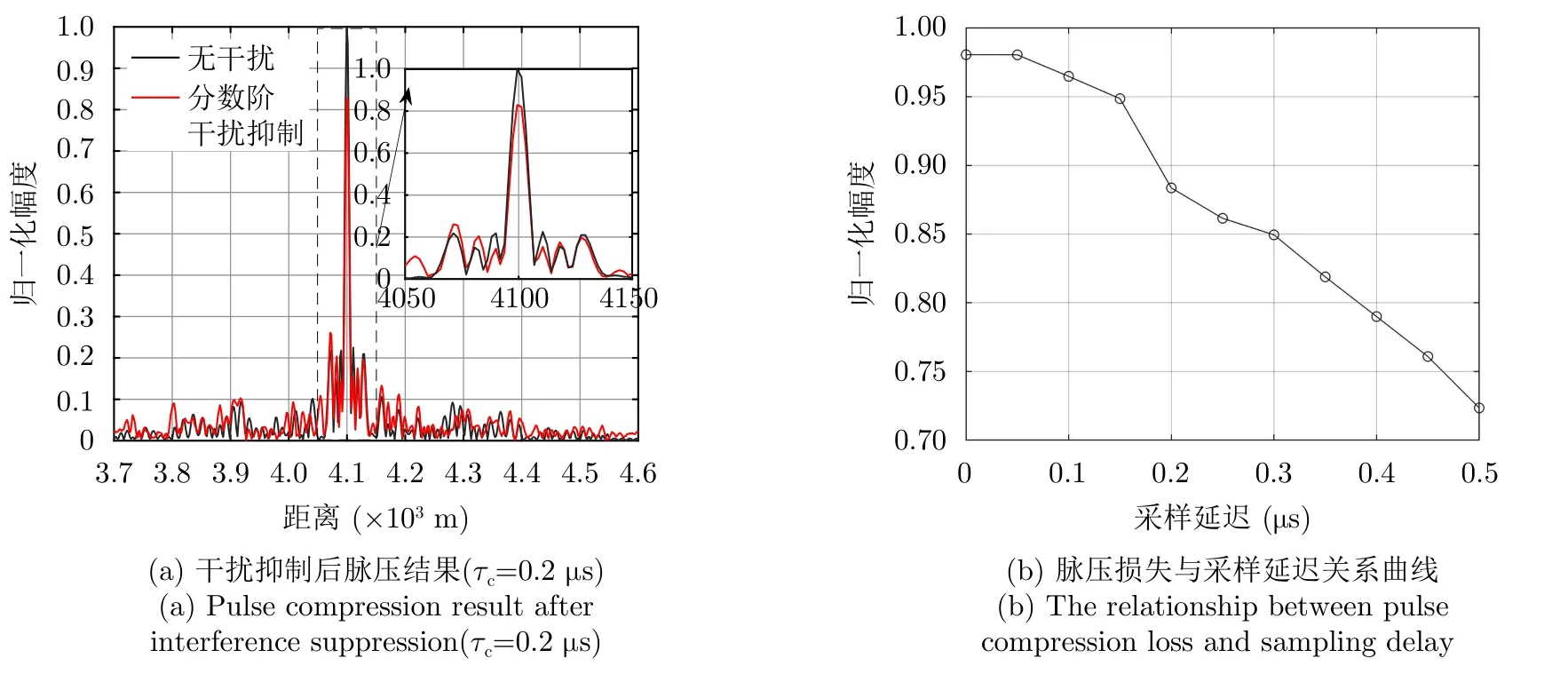
图10 干扰机非同步采样仿真结果Fig.10 Simulation results of asynchronous sampling by jammer

本文采用脉间-脉内捷变频信号以增强与干扰信号之间的区分度，但由于脉内子脉冲信号频率不连续，使得相邻子脉冲之间交叉项无法完全抵消，分段脉压处理后目标主瓣附近存在部分栅瓣。图11为无干扰条件下，采用表1所示雷达波形参数，当子脉冲个数M=4,10,20时的分段脉压输出结果。从图中可以看出，当子脉冲个数增加时，分段脉压带来的栅瓣在一定程度上有所降低，子脉冲从4个增加到20个，其分段脉压后最大栅瓣下降4 dB。图12表示采用不同的子脉冲数时，主副瓣比随信干比的变化关系曲线，其中信干比从–50～0 dB变化，其他仿真条件同仿真实验1，可以看到，随着信干比逐渐降低，主副瓣比在一定范围内波动，这表明副瓣仅为分段脉压引入的栅瓣，即低信干比条件下，本文所提方法仍可以有效抑制间歇采样转发干扰。

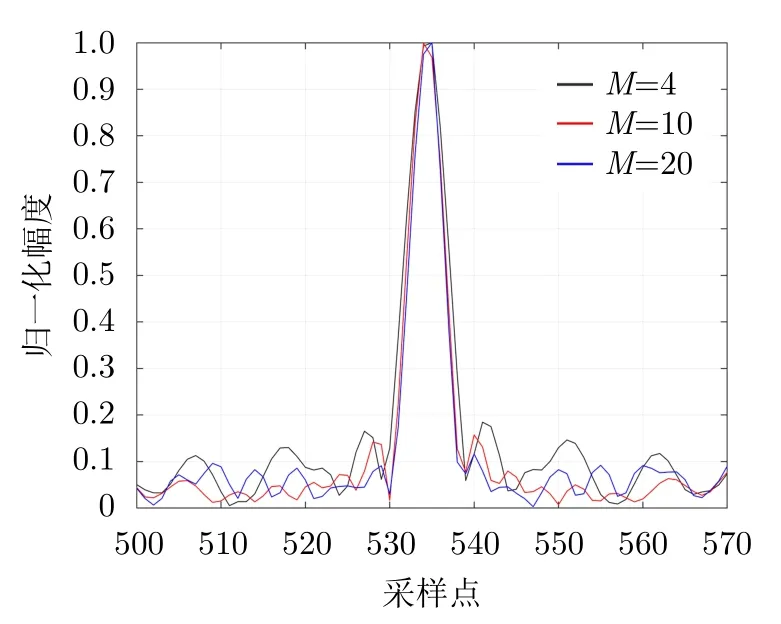
图11 不同子脉冲数分段脉压结果Fig.11 Pulse compression results of different sub-pulse numbers

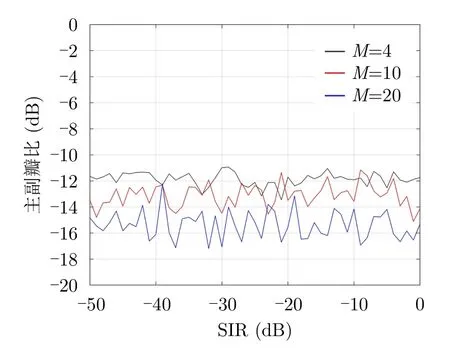
图12 主副瓣比随信干比变化关系曲线Fig.12 The curve of main-lobe to sidelobe ratio with SIR

7 结论

针对间歇采样转发干扰，本文结合脉间-脉内捷变频雷达波形优势，对受干扰的子脉冲在分数阶傅里叶域实现了干扰抑制。脉间-脉内捷变频波形的运用使雷达能够“主动”规避干扰频段，提升了雷达信号与干扰信号的区分度。对受干扰子脉冲进行提取和切片，在分数阶傅里叶域构造窄带滤波器组进行目标信号提取，从而达到抑制干扰的目的。最后通过分段脉压实现脉内积累。仿真结果表明，采用本文所提方法不仅可以有效对抗多主瓣干扰(不同间歇采样干扰样式组合)，且经过分段脉压后不会存在较大的幅度损失，有效提升了雷达的抗干扰能力。