一种相位域低积分旁瓣雷达波形优化方法

王鑫海 王超宇 张宁 陈伟

(中国船舶重工集团公司第七二四研究所 南京 211153)

1 引言

在雷达预警探测过程中，雷达波形起着非常重要的作用。对于脉冲压缩雷达，在相同功率和脉冲宽度的条件下，使用具有低副瓣水平的雷达波形，在测量目标与雷达距离时可获得更高的信噪比(Signal-to-Noise Ratio,SNR)增益[1]。通过分析雷达反射信号，可以提取与感兴趣目标相关的高价值信息。众所周知，雷达的性能一般由发射波形和接收处理方法两个重要因素决定[2]。本文主要研究了恒模波形设计方法。

为了获得最高发射功率，提高雷达对目标的探测性能，现代雷达的功率放大器通常工作在饱和状态。这就要求雷达波形的包络尽可能恒定。否则会导致发射波形失真，进而在接收端会导致匹配滤波器输出增益下降[3]。值得注意的是，为了能够提高脉冲压缩雷达的目标检测性能，理想的雷达波形应该具有逼近冲激形状的自相关函数[4]，这有助于雷达对小目标的探测。基于雷达、通信等系统对具有良好自相关性能波形的需求，早期研究学者通过解析构造、智能寻优等手段获得满足实际应用的波形序列，从二进制序列[5–11]逐渐延伸至多相码或恒模序列[12–17]。一些具有较好自相关特性的波形可以通过闭式表达式得到，如Frank序列[12]和Golomb序列[13]；一些基于智能寻优的波形序列优化方法有穷尽法[8]、遗传算法[9]、启发算法[11]和随机优化算法[13,14]等。这些算法计算量巨大，对长度大于等于103量级的序列优化是不实际的。使用传统的随机信号处理理论，自相关函数及其对应的功率谱密度(Power Spectral Density,PSD)构成了傅里叶变换对。在理想的条件下时域旁瓣为零的自相关函数意味着其对应的信号在频域中具有平坦的频谱，基于该结论，文献[18]和文献[19]分别提出了循环算法(Cyclic Algorithm-New,CAN)和周期性循环算法(Periodic CAN,PeCAN)两种迭代优化技术，可优化得到长度大于等于106量级且具有低自相关积分旁瓣的恒模非周期性和周期性序列。针对非凸优化问题，文献[20]和文献[21]分别利用基于MM (Majorisation-Minimisation)框架和随机优化技术实现了低自相关积分旁瓣电平(Integrated Sidelobe Level,ISL)波形优化。基于非线性约束优化框架，文献[22]提出了拉格朗日优化神经网络(Lagrange Programming Neural Network,LPNN)算法，获得了ISL性能水平低于–250 dB的波形序列。以上方案的共同缺点是计算复杂度高，尤其是LPNN的计算量异常庞大，不适合实际工程应用。为了提高优化效率，文献[23]利用交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)框架[24]对恒模波形进行高效的优化求解。该方法将复数域变量转换为实数变量，导致了优化变量维数加倍。为了处理恒模序列的优化问题，文献[25]利用共轭梯度法[26]对序列的相位进行优化求解，避免了直接处理恒模约束时出现的复杂计算过程。文献[27]提出了基于快速傅里叶变换的共轭梯度法对低ISL波形进行寻优，获得了最低ISL水平达–318 dB的周期性波形。文献[28]提出基于MM算法和投影梯度下降法(Projected Gradient Descent algorithm,PGD)的波形优化算法，获得了具有理想模糊函数的恒模波形序列。

为了获得具有类冲激自相关函数的恒模波形，本文提出了相位域坐标下降法(Phase-only Coordinate-Descent Method,PCDM)，将恒模约束优化问题转化为相位域无约束优化问题，规避非凸约束条件，简化了优化问题求解步骤。PCDM算法采用迭代更新的方式对变量进行优化求解，直至收敛。为了避免高维度变量梯度求解带来的较大复杂度，在每次迭代过程中，PCDM利用闭式解对波形序列进行更新，实现了优化变量的高效求解，且波形序列性能优于已有算法。

论文组织安排如下：第2节对低ISL的恒模波形优化问题进行详细描述；第3节提出了PCDM算法，推导了具体实现过程，并分析了计算复杂度；第4节通过数值仿真验证了所提出方法的有效性；第5节总结性归纳了本文所提算法的相关结论和未来可能的研究方向。

本文采用粗体小写字母表示矢量，用粗体大写字母表示矩阵；转置，共轭和共轭转置运算符分别用符号(·)T,(·)*和(·)H等表示；diag{A}定义为提取矩阵A对角线上元素，使之排列为一列矢量。矢量a的lp范数定义为‖a‖2；字母j作为虚数单位；对于复变量a，其实部和虚部分别表示为ℜ(a)和ℑ(a)；0M×N,1M×N和IN分别表示M×N的零矢量，M×N的全1矢量和N×N的单位矩阵。对于复数a,|a|和arg(a)分别表示a的模和相位参数。此外，缩写“s.t.”表示约束条件。

2 波形序列优化问题

本节针对具有低自相关旁瓣恒模波形优化问题的建模过程进行详细介绍。假设s=[s0,s1,...,sN−1]T表示均匀采样长度为N的雷达波形序列。在不失一般性条件下，将序列的幅值固定为1，即[15]

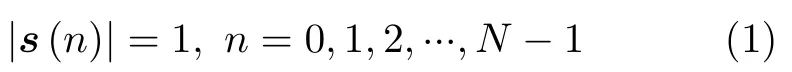
如果s是周期信号，则它的自相关函数定义为

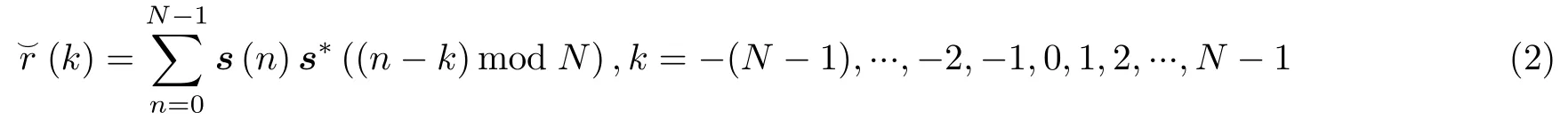
其中，mod为取模算子。类似地，非周期信号sa的自相关函数定义为

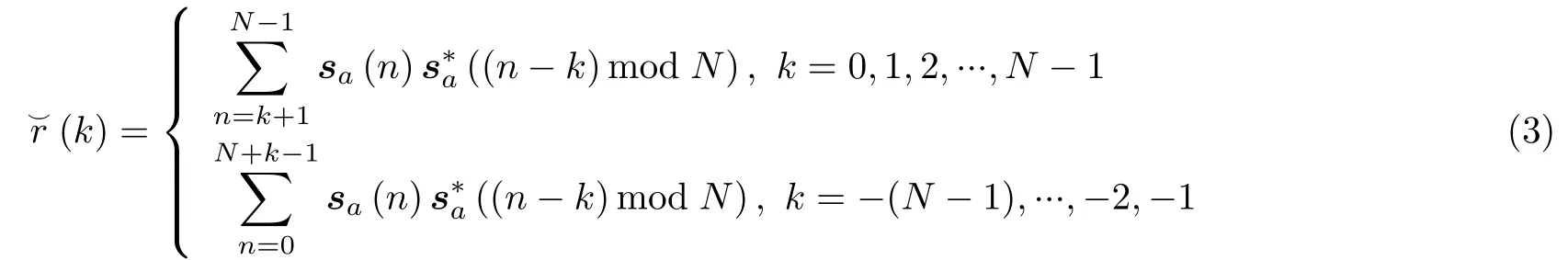
则关于复数恒模波形序列的最小化ISL优化问题可表示为

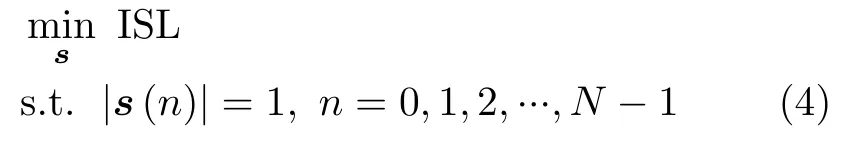
本文首先以周期波形为例对低ISL周期波形优化问题进行建模，相关结论可用于非周期波形的设计。以最小化ISL为目标函数的优化问题表示

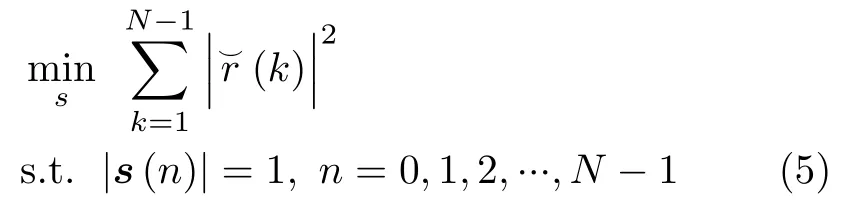
其中，目标函数即为波形序列自相关函数所有副瓣电平的平方和。

基于零自相关旁瓣波形序列具有平坦的功率谱这一结论，最小化ISL优化问题的目标函数可以进行频域表示。根据Parseval定理，波形的ISL时域形式可以等价地在频域中表示[18,19]，具体数学表示形式为

其中，u(k)是s(n)的离散傅里叶变换(Discrete Fourier Transform,DFT)，即

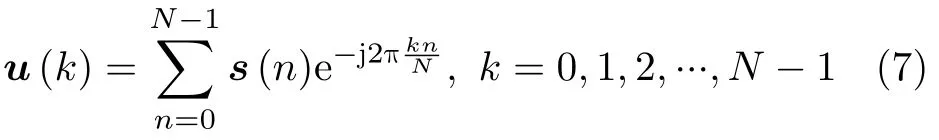
为了规避求解4次多项式最小化的问题，可将基于功率谱密度表示的目标函数等价为表示频谱幅度的形式，具体数学表达形式为[18]

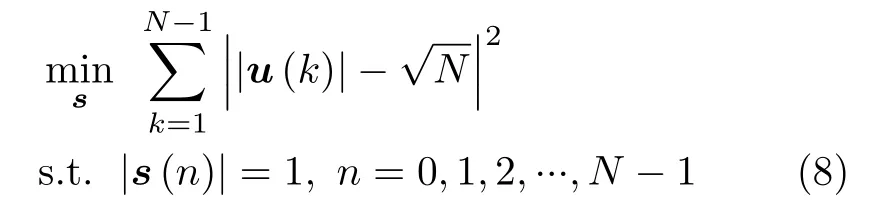
令离散傅里叶基矢量为

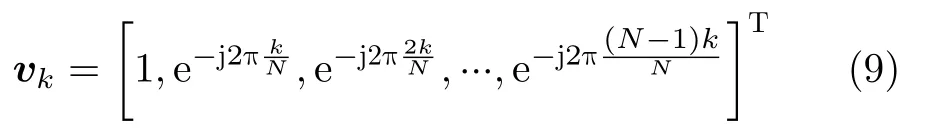
因此，u(k)矢量形式可表示为u(k)=。进一步地，若n点DFT基矩阵可为

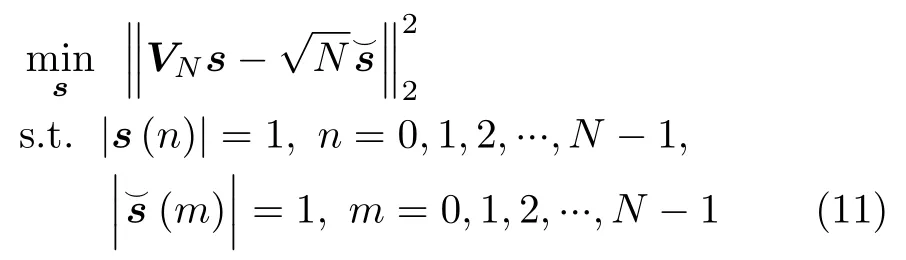
然后，式(11)更为紧凑的表达式为[23]

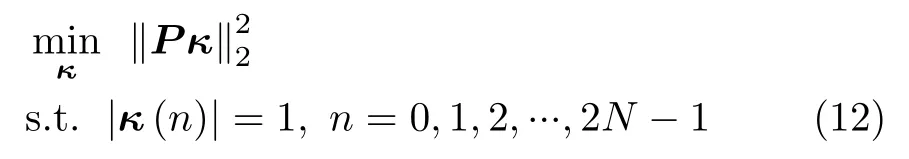
其中，P和κ可分别构造为

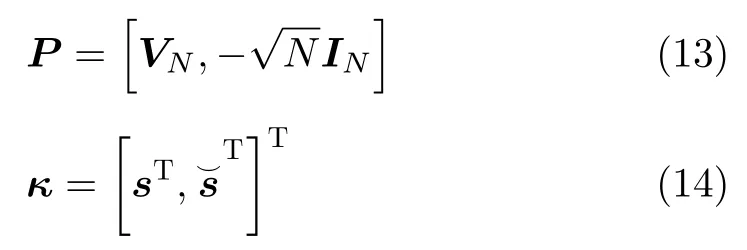
由于恒模约束条件为非凸集，故式(12)为非凸优化问题。

借鉴以上推导方法，非周期波形序列优化问题可表示为

3 相位域坐标下降法(Phase-only Coordinate-Descent Method,PCDM)

以周期波形优化问题(12)为例，通过观察式(12)可将其目标函数展开，则式(12)可转换为

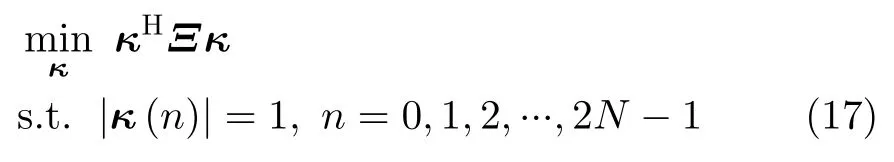
其中，Ξ=PHP。同理，优化问题(15)可转换为与式(17)结构相似的等价问题。

式(17)中的恒模约束为非凸约束，无法借助CVX[29],Sedumi[30]等凸优化工具直接求解。为了将式(17)转化为无约束优化问题，避免恒模约束所带来的复杂计算过程，本节提出了相位域坐标下降法求解恒模波形。PCDM算法将优化变量κ转换为其对应相位组成的相位变量，因此，可将恒模约束优化问题转化为相位域的无约束优化问题。本节借助坐标下降法思想分析了κ中各元素相位行为与目标函数的解析关系，从而以最小化目标函数为准则确定当前元素的相位表达式，即用其他元素表示当前元素的最优值。为了找到κ(i)与目标函数κHΞκ的关系，以周期波形优化问题(17)为例，从目标函数中提取第i个元素κ(i)作为自变量，经整理κHΞκ可展开为

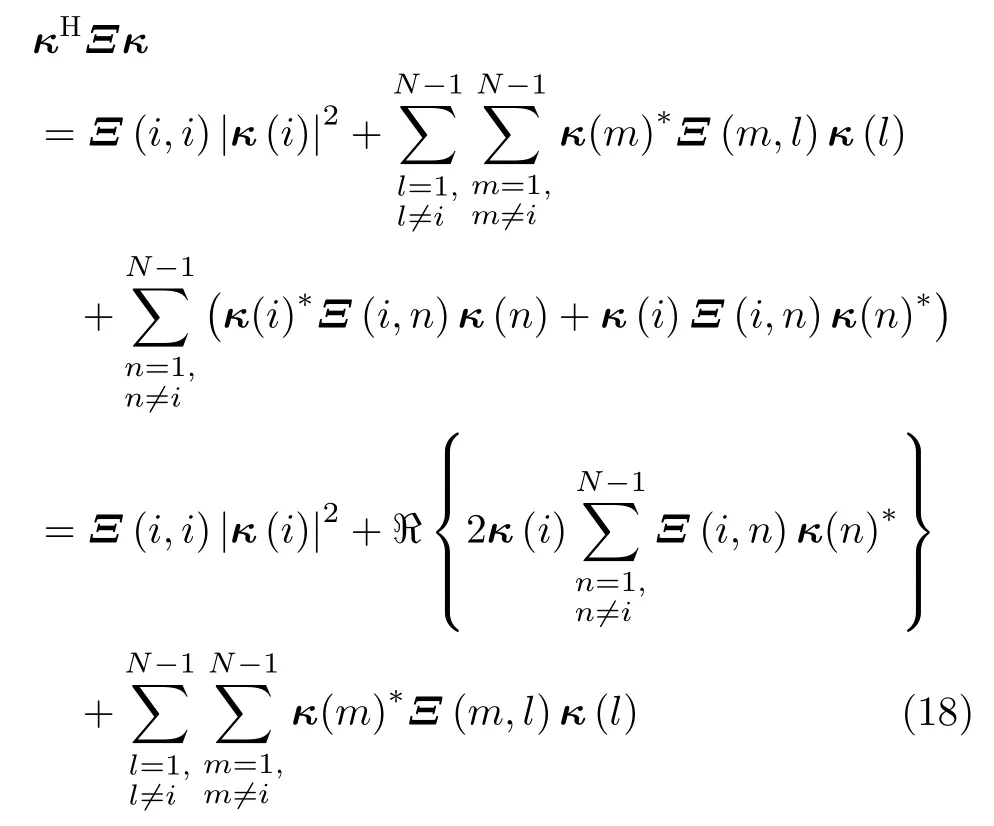
由式(18)可见，κ(i)模值已知，则第1项与κ(i)优化无关，第3项为常数，因此只有第2项决定了κ(i)与目标函数值的关系。此时针对κ(i)构造子优化问题为

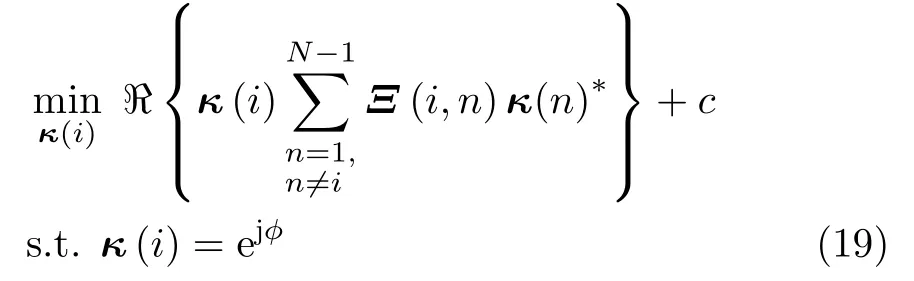
此时对κ(i)更新时，其余(2N–1)个元素是固定的，可对其进行单独求解，则子问题(19)中κ(i)最优解的表达式为

其中

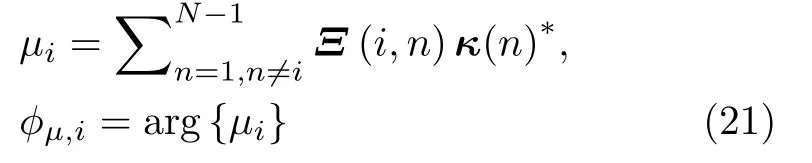
对于维度为2N的优化变量κ，优化问题(16)的一次迭代可以分解为2N个关于一维优化变量的子优化问题。一次迭代过程可对κ中所有元素更新，通过循环迭代的方式对κ的相位向量进行多次迭代寻优，直至满足终止条件，最终得到κ的优化结果κ†，从而得到最终的优化波形s†=κ†(0:N −1)。综上所述，PCDM算法对顺序优化κ(0),κ(1),···,κ(2N−1)的过程可逐一实现，直到满足收敛条件，相应的计算复杂度为完整的PCDM算法过程见表1(以求解式(17)为例)。

表1 PCDM算法Tab.1 PCDM algorithm

4 数值仿真

本节将PCDM算法与现有的基于ADMM低ISL波形设计算法[23]进行了比较。通过MATLAB仿真手段对两种算法优化后的波形自相关积分旁瓣电平进行比较，验证PCDM算法的有效性，并通过运行时间(由于计算机配置不同，运算时间统计结果可能与其他文献结果存在差异，本文意在通过统计不同算法在同一平台的运行时间，比较不同算法的运算效率)的对比，说明PCDM算法在降低计算复杂度上的优势。仿真参数设置：周期与非周期波形序列长度均为1 2 8；计算机配置为I n t e l(R)Core(TM) i5-7500 CPU @ 3.40 GHz，内存4 GB；对ADMM的数据统计结果由本文方法复现所得，虽与文献[23]中数据略有差异，但基本保持一致。

由于解决非凸优化问题时优化与初始输入有关，故本文分别对ADMM算法与PCDM算法做了600次随机试验，每次试验对两种算法输入相同初始变量，设置相同的收敛参数，如表2所示，最终得到的周期波形序列的自相关函数如图1所示，同时对ISL水平低于–250 dB的波形数量进行了统计，并计算了其在所有产生波形数量中的占比。从随机试验最终结果可知：ADMM算法的最优波形与PCDM算法得到的最优波形的ISL分别可达–285.2 dB和–320.2 dB；对于ISL小于–250 dB的序列占比，ADMM算法所得到的波形序列数量在总试验次数中所占比例可达73.83%，PCDM算法的波形序列数量在总试验次数中占比可达到82.20%；ADMM算法和PCDM算法所有序列的平均自相关函数如图2所示，ADMM算法优化序列的平均自相关积分旁瓣经统计约为–253.2 dB，PCDM算法所得到所有波形的自相关函数ISL平均值经统计为–256.9 dB。因此，基于大量试验的统计结果，PCDM算法均优于ADMM算法，且所获得最低波形ISL水平优于参考文献[27]。

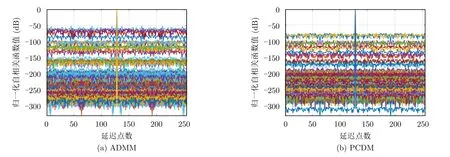
图1 ADMM算法与PCDM算法得到周期波形所对应的自相关函数Fig.1 Comparison of the autocorrelations of the periodic waveforms obtained by different methods:ADMM and PCDM

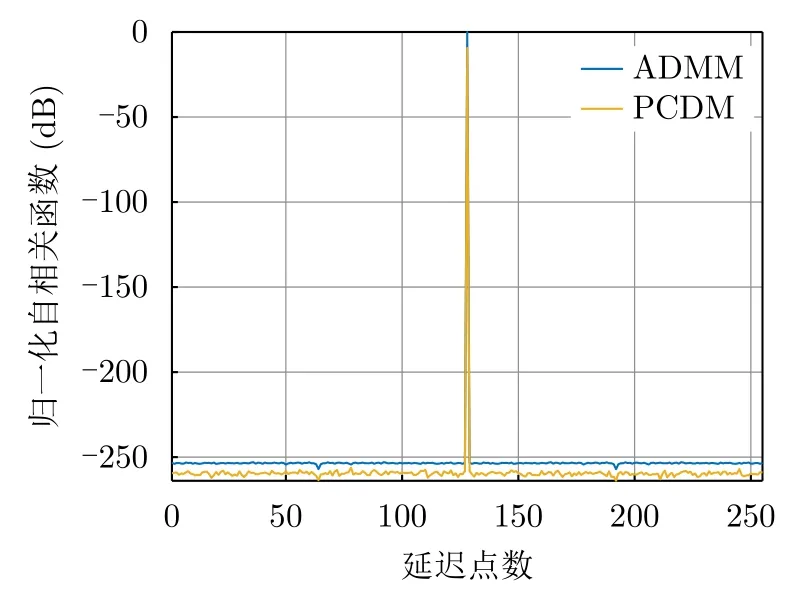
图2 ADMM算法与PCDM算法得到周期波形所对应的平均自相关函数Fig.2 Comparison of the average autocorrelations of the periodic waveforms obtained by ADMM and PCDM

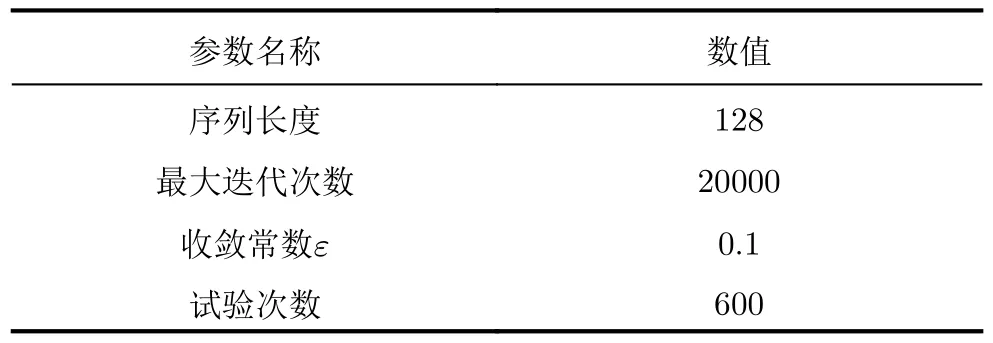
表2 周期波形优化两种算法所用参数Tab.2 Parameters used in two algorithms in periodic waveform optimization

为了验证PCDM算法收敛性能，图3给出了在相同初始值和迭代终止条件下，ADMM算法与PCDM算法在迭代优化周期波形过程中目标函数值的变化情况，在波形序列长度为128和1024两种情况下，PCDM收敛速度均比ADMM算法的收敛快，且具有更低的收敛值。

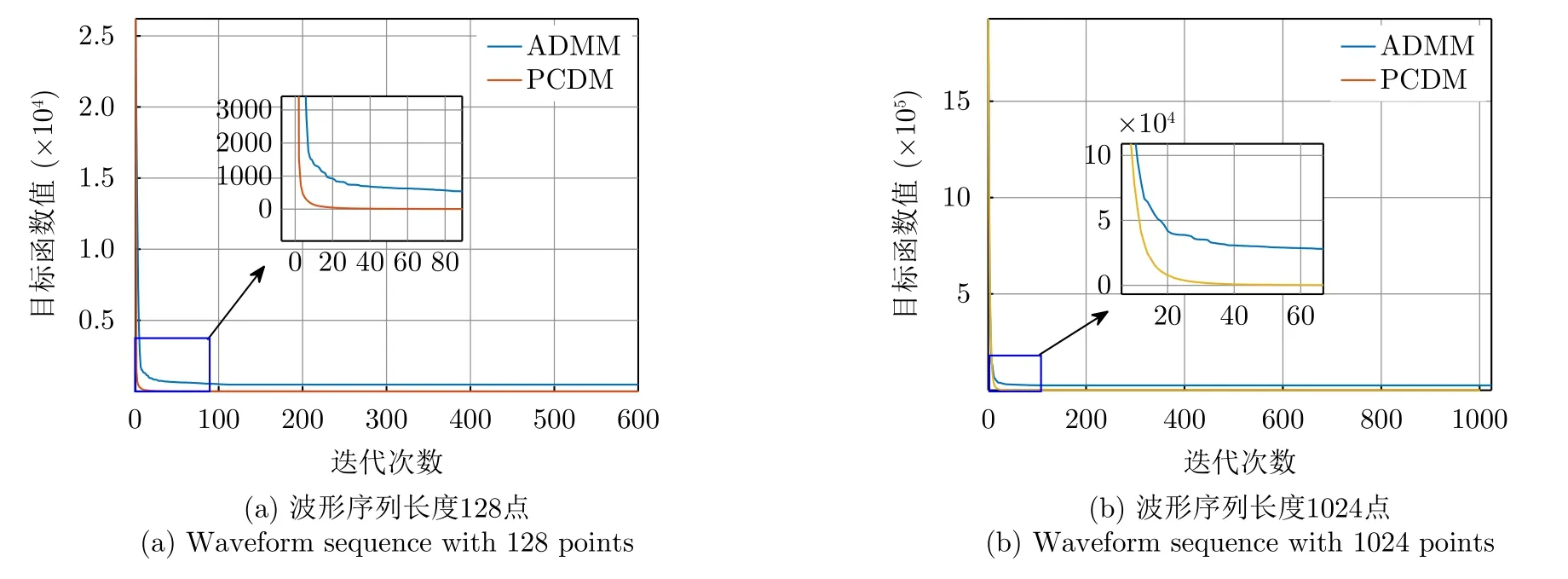
图3 ADMM算法与PCDM算法优化周期波形过程的收敛性能Fig.3 The convergence performance of optimizing the period waveform using the different methods:ADMM and PCDM

为了进一步评估算法运算效率，两种算法的计算时间如表3所示。结果表明，PCDM算法相比ADMM算法耗费时间少4.7206 s(波形序列长度为128时)和157.1160 s(序列长度为1024时)，PCDM算法的运算速度更快。

表3 对于周期波形优化ADMM算法与PCDM算法运算耗时比较Tab.3 Comparison of the computational time of ADMM and PCDM(Period)

对于非周期信号优化设计，ADMM算法与PCDM算法所得最优序列的自相关函数如图4所示。在相同初始值和迭代终止条件下，600次随机试验中，ADMM所得波形序列的最低ISL为–24.3 dB，PCDM所得波形序列的最低ISL为–26.89 dB。因此，PCDM算法结果优于ADMM算法。由于受波形序列恒模特性的影响，两种算法所得到的波形自相关函数最远离主瓣的位置始终保持在–42.1442 dB。图5给出了ADMM算法与PCDM算法所对应的600次试验下的平均自相关函数，ADMM算法所得的波形序列自相关副瓣起伏较大，最接近和最远离主瓣区域的电平较低，较远离主瓣区域的副瓣电平较高，而PCDM算法得到的最优波形对应的自相关函数副瓣相对比较平稳，更有利于雷达的目标检测等应用。

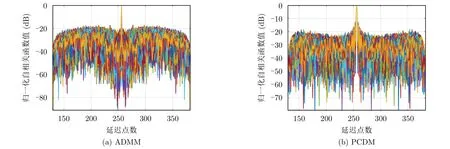
图4 ADMM算法与PCDM算法得到非周期波形所对应的自相关函数Fig.4 Comparison of the autocorrelations of the aperiod waveforms obtained by different methods:ADMM and PCDM

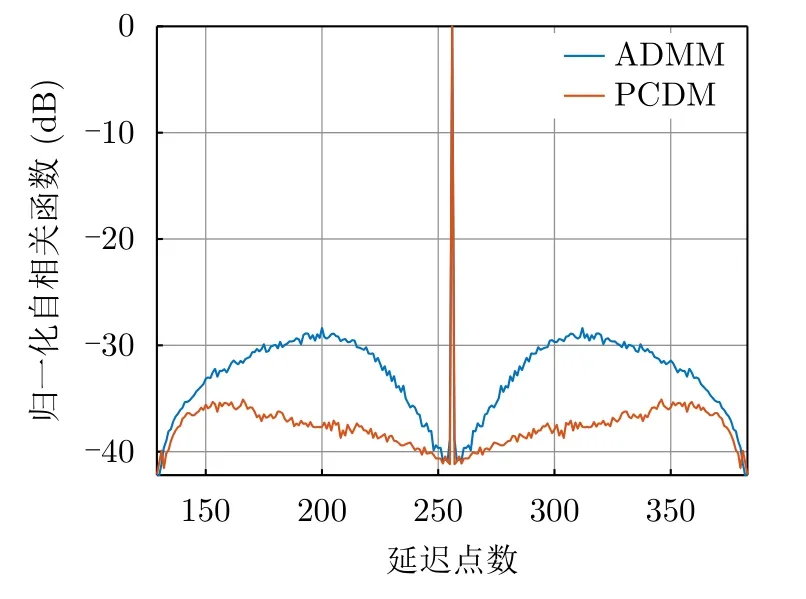
图5 ADMM算法与PCDM算法得到非周期波形所对应的平均自相关函数Fig.5 Comparison of the average autocorrelations of the aperiod waveforms obtained by ADMM and PCDM

图6给出了相同初始值和迭代终止条件下，ADMM算法与PCDM算法优化非周期函数的收敛曲线。从放大图可以看出，PCDM算法与ADMM算法的目标函数最终收敛值几乎相同，然而PCDM下降速率明显较快。

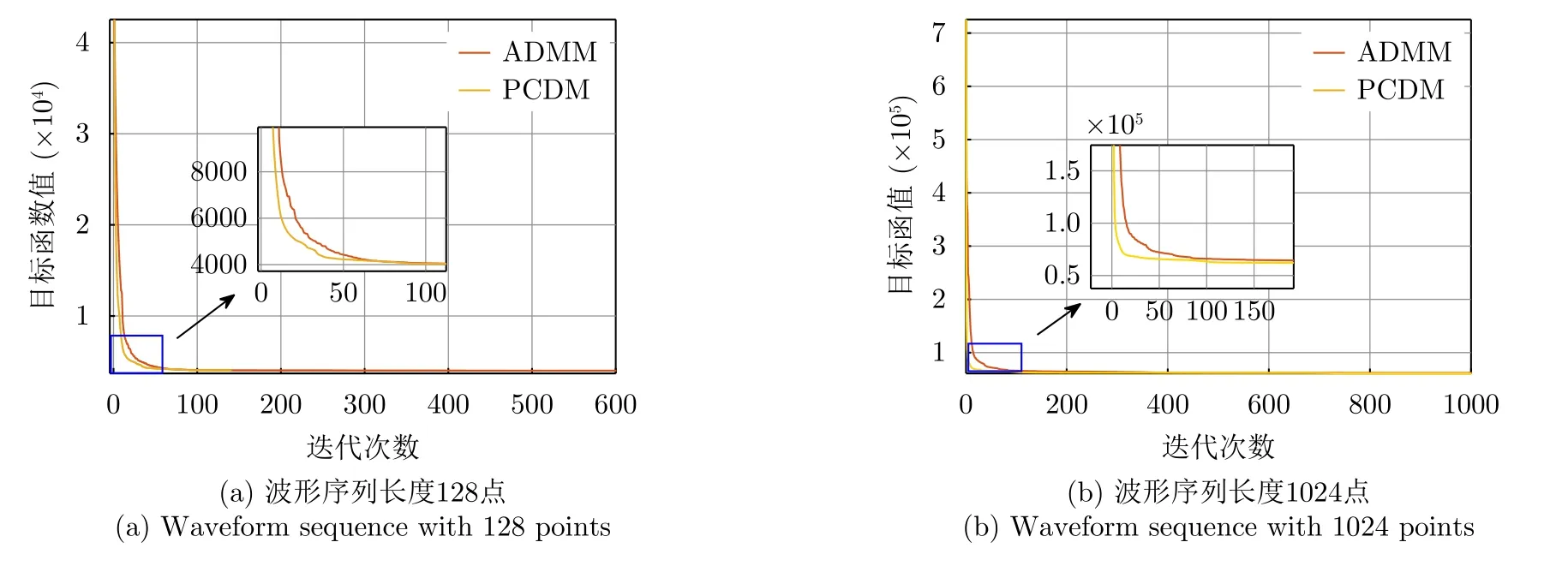
图6 ADMM算法与PCDM算法优化非周期波形过程的收敛性能Fig.6 The convergence performance of optimizing the aperiod waveform using the different methods:ADMM and PCDM

在优化非周期波形时，两种算法的运行时间统计如表4所示。结果表明，PCDM算法相比ADMM算法耗费时间少46.9838 s(序列长度为128时)和560.3848 s(序列长度为1024时)，PCDM算法运算速度更快。

表4 对非周期波形ADMM算法与PCDM算法运算耗时比较Tab.4 Comparison of the computational time of ADMM and PCDM (Aperiod)

通过以上比较可知，本文所提的PCDM算法相比于ADMM算法可以以更大概率获得低ISL波形，并且计算效率更高。一方面，ADMM算法求解时所考虑的可行集包含了波形幅度与相位两个维度，而PCDM算法仅以波形的相位域矢量集为可行域，寻优范围大大缩小，故使用PCDM算法更容易获得低ISL波形序列，且收敛速度更快；另一方面，坐标下降法在每一次迭代中采用闭式解更新变量，规避了求解高维向量梯度，故可进一步提升波形优化效率。

模糊函数是分析波形性质的基本工具。图7和图8分别给出了ADMM与PCDM算法所获得的周期信号和非周期信号的模糊函数图。通过比较图7(a)和图7(b)及图8(a)和图8(b)，可知ADMM与PCDM算法所得的波形在零多普勒切面处均有凹陷，这是由于两种算法所得波形具有多普勒敏感性。在零多普勒切面处，多普勒频率对波形自相关无影响，波形具有低自相关积分旁瓣；而在多普勒非零切面，由于多普勒频率的调制作用，改变了波形的自相关特性，抬高了波形的自相关积分旁瓣水平。图7(a)和图8(a)中零多普勒附近模糊函数幅度小于0.1的最小归一化多普勒宽度分别为0.26,0.14，图7(b)和图8(b)中零多普勒附近模糊函数幅度小于0.1的最小归一化多普勒宽度分别为0.38和0.19。相比于ADMM算法所得波形，PCDM算法所得波形对应的模糊函数小于0.1的最小归一化多普勒宽度增加了46.15%(周期波形)和35.71%(非周期波形)，这说明对于周期/非周期波形在零多普勒附近，PCDM算法所得波形对多普勒调制的容忍性更优。通过比较图7(a)和图8(a)、图7(b)和图8(b)，周期信号相比于非周期波形，模糊函数在零多普勒切面具有更低的自相关积分旁瓣。这是由于在求解优化问题过程中，周期波形序列中的所有元素均在参与自相关函数的计算，而非周期波形序列中参与自相关函数计算过程中元素数量随着偏移量绝对值的增加而逐渐减少，导致周期波形相对于非周期波形具有更多的自由度，故可以获得更低的目标函数值，即更低的自相关积分旁瓣。

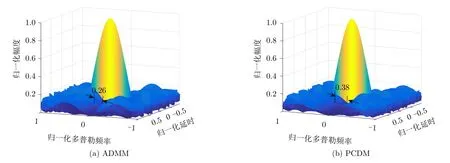
图7 ADMM与PCDM算法最优周期波形的模糊函数Fig.7 The ambiguity function of the periodic waveform obtained by the different methods:ADMM and PCDM

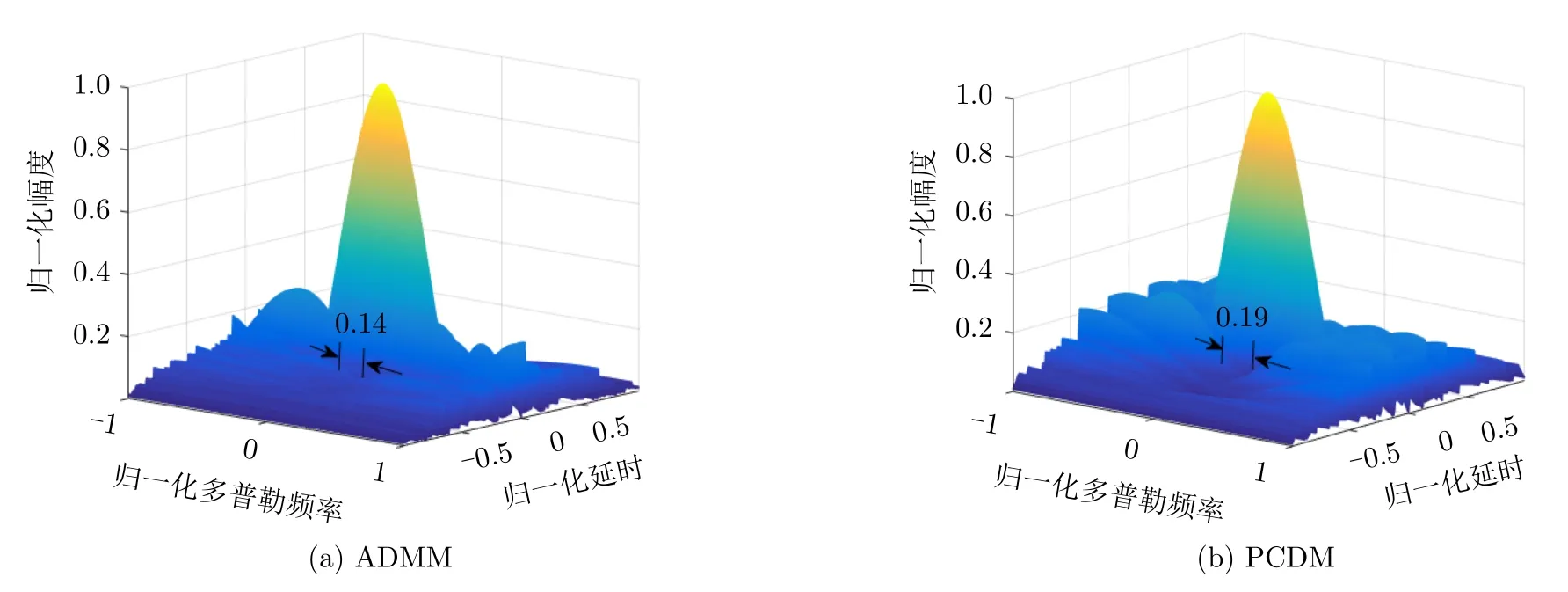
图8 ADMM与PCDM算法最优非周期波形的模糊函数Fig.8 The ambiguity function of the aperiodic waveform obtained by the different methods:ADMM and PCDM

5 结论

针对恒模约束下低自相关积分旁瓣波形设计问题的非凸性所带来的计算复杂度高的问题，本文提出了相位域低ISL恒模波形的优化设计算法—PCDM算法。PCDM算法将带约束的优化问题转换为无约束优化问题，并通过计算闭式解达到快速迭代优化波形的目的，即将恒模序列对应的相位矢量作为优化变量，将原优化问题转化为相位域内的无约束优化问题，减小计算难度。仿真结果表明，PCDM算法优化波形得到的自相关性能优于现有的基于ADMM算法的最优解的自相关性能。与ADMM算法相比，PCDM算法计算复杂度更低。未来研究重点将聚焦在控制波形自相关形状方面的波形快速设计问题，并针对新体制雷达对波形提出的新需求，开展进一步探索。