短基线收发分置频域协同波形设计方法

余显祥 路晴辉 杨婧 沙明辉 崔国龙* 孔令讲

①(电子科技大学信息与通信工程学院 成都 611731)

②(北京无线电测量研究所 北京 100854)

1 引言

电子新技术的快速发展使得各种复杂有源干扰不断涌现，严重制约了雷达探测威力。如何发展具有高探测性能和高抗干扰能力于一体的新型雷达体制与技术变得尤其重要[1]。在雷达干扰和抗干扰的长期博弈中，雷达抗干扰措施愈加丰富，主要可以分为主动抗干扰和被动抗干扰两类[2]。其中，主动抗干扰是指雷达主动发射某种信号欺骗敌方的干扰导引，使得敌方不能及时发现和准确识别真正用于探测的雷达信号；被动抗干扰是指在已经存在干扰信号的情况下，雷达采用先进的信号处理方式等手段降低干扰的影响。本文将围绕主动抗干扰方法展开研究。

雷达主动抗干扰方法可以通过单部雷达或者多节点协同实现。针对不同的场景和特定任务需求，单部雷达主动抗干扰方法可以在时域、频域、极化域等多域设计掩护信号和真正雷达信号的发射参数[3–7]。例如，文献[3]提出“虚假掩护信号+被掩护信号”、“虚假掩护信号+被掩护信号+虚假掩护信号”的时域设计准则，通过在不同的时序发射虚假掩护信号和被掩护信号，使得被掩护信号受到的干扰时间缩短。文献[4]利用高功率掩护信号对低功率探测信号的增益压制作用，减弱有源转发干扰中的探测信号功率，实现雷达抗有源转发干扰。文献[5]通过在探测脉冲前设计一个宽脉冲掩护信号或者脉宽相同、频率不同的掩护信号，有效对抗短存储模式下的应答式干扰。然而，未来复杂的电磁环境将对雷达的目标检测、低截获和抗干扰性能具有更高的要求，单部雷达发射的低截获、抗干扰波形将很难应对强对抗、快转发等复杂作战场景。分布式多雷达可以构成全方位、立体化、多层次的体系，使传统的“一对一”有源压制干扰和欺骗干扰性能大大降低[8]。文献[9]利用地面雷达和弹载雷达信号层面的协同，以双站雷达有源跟踪时的发射信号作为参考信号，根据两雷达与接收信号之间的相似度进行干扰类型的判别。文献[10]利用雷达有源诱饵辐射使敌方雷达判定为真目标的假回波，防止己方雷达被敌方雷达跟踪和雷达制导武器击中。相比于单部雷达，多节点协同可提供更高的抗干扰自由度且抗干扰性能更好。因此，开展多节点协同主动抗干扰技术研究具有重要的价值。

本文提出一种适用于近中程目标探测场景的短基线(目标相对发射节点位于远场)多节点频域协同抗干扰波形设计方法，为未来智能化雷达抗干扰波形设计研究提供全新的思路。具体而言，分别设计发射节点的宽带掩护信号和收/发节点的窄带探测信号，使其满足在频域具有正交性，此外，宽带和窄带信号通过有线电缆控制同时同方向协同发射，实现宽带信号对窄带探测信号的掩护，从而降低窄带探测信号所在频谱被干扰的概率。同时，窄带波形满足良好自相关特性以提升目标检测性能。

2 信号模型

如图1所示，当环境中存在多种强对抗、快转发的干扰时，单一的应对某种干扰的发射波形不满足应用需求。通过分析短基线收发分置系统在可用频段范围内的受干扰程度大小，选择合适的发射信号频点，采取频域协同波形设计策略优化发射波形，最终实现主动抗干扰。其中，频域协同波形设计策略具体是指两个短基线节点通过有线电缆控制时序统一，实现同时同方向协同发射，其中一个发射节点发射宽带掩护信号，另一个收/发节点发射窄带探测信号，并在收/发节点的信号处理过程中实现回波信号的窄带接收。宽带掩护信号将窄带探测信号掩护在其频谱中，使得截获接收机无法从接收到的宽带信号中精确识别出窄带探测信号，进而不能发射瞄准探测信号频率的压制干扰信号，最终实现雷达低截获和抗干扰性能的提升。

图1 频域协同波形示意图Fig.1 Schematic diagram of frequency domain cooperative waveform

具体地，假设收/发节点发射脉间频率捷变的N个窄带脉冲信号：

fz ∈{f1,f2,...,fZ}表示脉间跳频频点(可跳变的频点共Z个)，此外，收/发节点发射的窄带脉冲信号呈现出周期性变化，其中，脉冲数n和 跳频频点z满足：

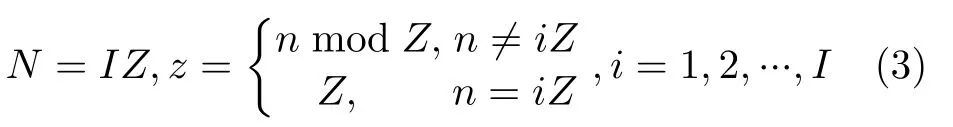
其中，mod表示取余。

由于收/发节点发射脉间频率捷变的脉冲信号，宽带信号为掩护窄带探测信号需要针对不同的窄带脉冲信号设计相对应的掩护信号，并保证协同波形在频域表现为平坦分布。发射节点发射的宽带脉冲信号表示为

因此，两部短基线节点发射的频域协同信号S(t)可以表示为

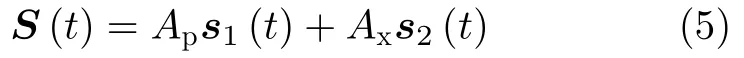
其中，Ap表示窄带信号幅度，Ax表示宽带信号幅度。

如图2所示，本文首先假设宽带掩护信号的功率谱密度(Power Spectral Density,PSD)(如图2中(b)所示)可以近似为图2中(a)的矩形形式，其中平均幅度为Afw；如图2中(d)所示的窄带探测信号PSD近似为图2中(c)的矩形形式，其幅度为Afn。为了使得频域协同波形S(t)的PSD相对平坦分布，需满足：

图2 频域协同波形功率配置原理示意图Fig.2 Schematic diagram of frequency domain cooperative waveform power configuration

根据帕斯瓦尔定理以及上述假设，频域协同两信号的幅度和带宽应满足如下关系：

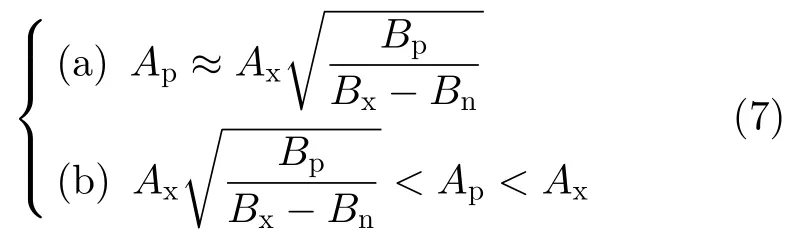
其中，条件(a)是为了保证窄带信号s1(t)的PSD幅度峰值与宽带信号s2(t)的PSD幅度平均值相近，从而保证信号S(t)的PSD相对平坦，使得敌方雷达不易从频域分离出窄带探测信号；条件(b)的不等式右侧从功率的角度保证了宽带信号对窄带信号的掩护，同时不等式左侧提升了窄带信号的目标探测能力。

本文所提出的频域协同波形设计方法尽管未考虑利用宽带信号进行探测，但其仍具有一定的实际应用价值。例如，由于窄带探测信号幅度小于宽带掩护信号幅度且窄带探测信号需要实现双程传播，因此，近中程(近程一般在50 km以内、中程一般在50～200 km以内)目标探测并不需要高功率需求时，可以牺牲宽带信号功率以掩护窄带雷达进行隐蔽探测。

另外，相比单雷达波形频域协同方法，所提方法主要具备以下优势：

(1) 波形产生易实现：采用两个节点分别发射恒模信号，相比于单节点发射两个信号，非线性放大器工作在临近饱和状态，避免了波形的非线性失真。

(2) 抗截获性能高：本文提出的方法为两个节点同时发射频域协同的波形，且窄带探测信号在特定频点跳变，使得窄带探测信号被截获和干扰的概率进一步降低。

(3) 抗摧毁能力强：若采用单部雷达进行频域协同，信号一旦被敌方截获，将面临被干扰或者被打击的危险。若采用短基线收发分置系统，宽带发射节点尽管面临被摧毁的危险，但仍降低了另外一个收/发节点被打击的可能。

3 频域协同波形设计方法

在本节中，根据上述信号模型，将分别针对频域协同波形中的窄带信号和宽带信号进行优化设计。

3.1 窄带探测信号设计方法

3.1.1 问题模型

假设收/发节点的基带信号p(t)可以离散化表示为

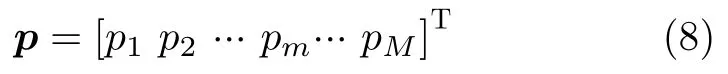
其中，pm=ejφm，则序列p的非周期自相关函数[11]表示为

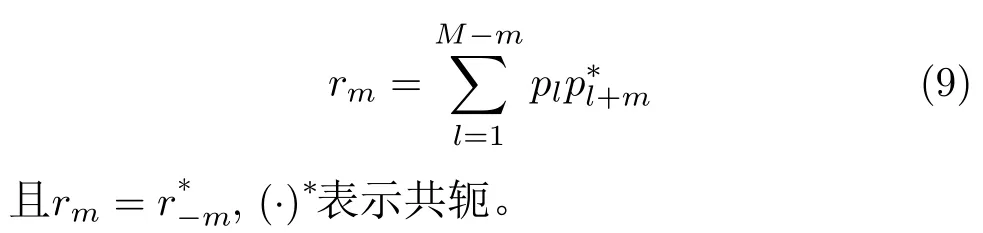
针对窄带探测信号的设计，本文将重点考虑最小化感兴趣区域自相关峰值旁瓣电平，抑制强目标返回的旁瓣能量，提高多目标情况下弱目标的检测性能[12]，则具体问题模型表示为

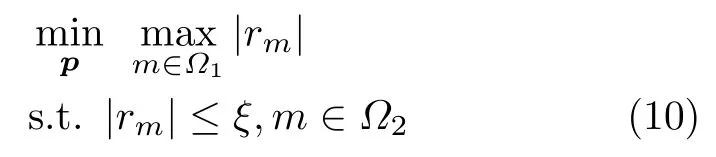
其中，|·|表示绝对值，Ω1,Ω2分别表示局部自相关函数峰值抑制区域和其他自相关函数区域，ξ表示Ω2区域约束的上界电平。

根据峰值幅度等价变换原理[13]，优化问题(10)目标函数可以表示为lq-范数问题：

其中，q ≥2表示lq-范数，

因此，在考虑恒模约束的情况下，该问题模型可以表示为

3.1.2 问题求解

上述优化问题Pp是一个在多项式时间内求解困难的lq-范数问题，并包含非凸约束，因此，本文提出一种MM-PMM算法，以迭代求解该优化问题。其实质是将原问题拆分为3个易于求解的子优化问题并行迭代计算，并利用MM (Majorization-Minimization)算法的近似原理将lq-范数问题转换为二次函数优化问题[14,15]。

考虑到一个序列的自相关和PSD是一对傅里叶变换对(FFT{f(t)⊗g(t)}=F(w1)G(w2)，其中⊗表示卷积)的关系[16]，则自相关函数可以用快速傅里叶变换(Fast Fourier Transform,FFT)和逆快速傅里叶变换(Inverse Fast Fourier Transform,IFFT)的方法表示为

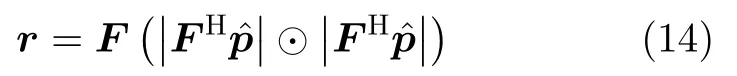
其中，⊙表示对应元素相乘，F=[f0f1...fL−1]。则问题Pp改写为

上述优化问题的近端增广拉格朗日函数[17]可以表示为

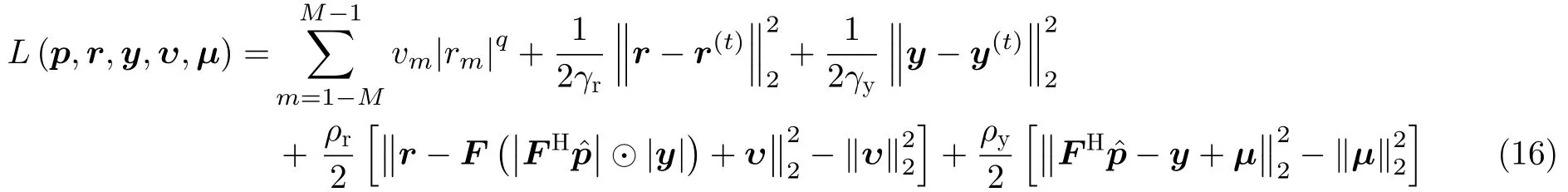
其中，γr,γy为近端参数，ρr,ρy为惩罚参数，υ,µ为扩展对偶变量，r(t),y(t)表示第t次迭代的结果。

设第t次迭代得到{p(t),r(t),y(t),υ(t),µ(t)}，则(t+1)次迭代通过以下步骤进行更新：

(1) 更新p(t+1)：

与p有 关的子优化问题化简为

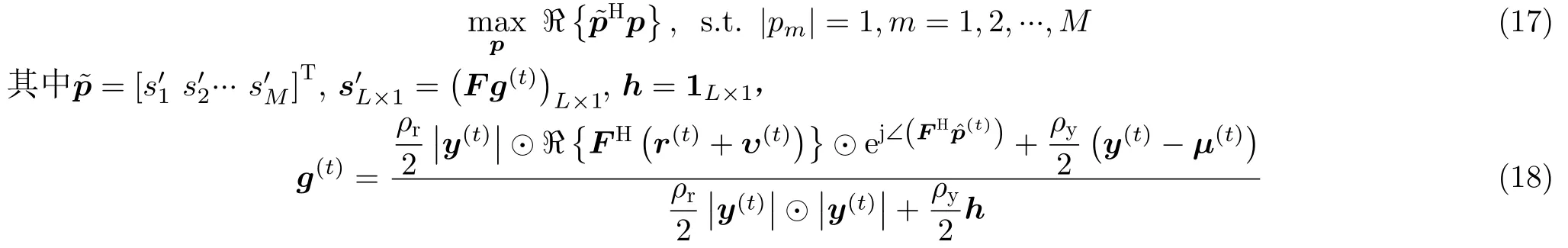
上述优化问题(17)的闭式解为

(2) 更新r(t+1)：

(3) 更新y(t+1)：

关于y的子优化问题可以化简为

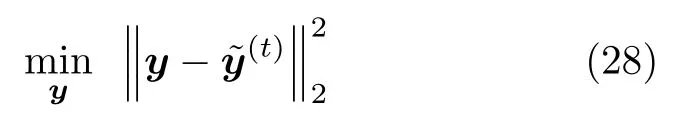
其中，

该算法的求解过程中主要用到FFT,IFFT和向量乘法。更新p(t+1)步骤中式(18)的计算复杂度为O(3LlogL+4L)；更新r(t+1)步骤中计算复杂度为O(2LlogL+3L)；更新y(t+1)步骤中计算复杂度为O(2LlogL+4L)；更新υ(t+1),µ(t+1)的计算复杂度分别为O(2LlogL+L)和O(LlogL)。因此，在MM-PMM算法一次迭代过程中的计算复杂度为O(10LlogL+12L+I(L))。

除了本文提出的MM-PMM算法，坐标下降(Coordinate Descent,CD)等算法[18]也是求解这类问题的常见方法。根据式(13)和式(20)可知，根据MM原理，原优化问题Pp将近似为关于p的4次问题，采用CD算法求解的计算复杂度为O值得注意的是，本文提出的算法引入辅助变量r和y，避免了求解关于p的4次问题，计算复杂度低于CD算法。

3.2 宽带掩护信号设计方法

假设发射节点发射的宽带基带信号xz(t)可以离散化表示为

其L(L ≥K)点傅里叶变换频谱可以表示为

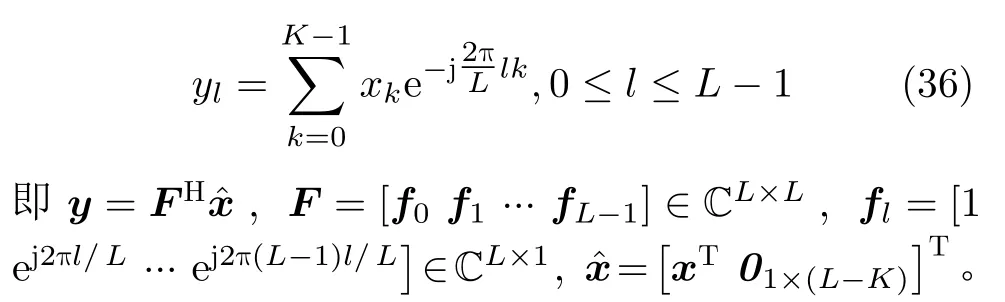
为了在接收信号处理时能够在频域分离出窄带信号，设计如图3所示的和窄带探测信号重叠部分的宽带信号频谱包络形状，使得该区域的频谱幅度逼近设定的包络值。这类问题的求解在通过优化发射信号解决频谱拥挤问题中较为常见[19–21]，例如，文献[19]建立恒模约束下的波形频谱与期望频谱形状加权匹配的加权最小二乘匹配问题，并提出间接优化方法和直接优化方法两种算法求解该问题。

图3 宽带掩护信号频域特性Fig.3 Frequency domain characteristics of wideband cover signal

针对上述频谱需求，该问题模型的目标函数可以表示为

其中，Ω表示宽带信号的阻带区域集合，εl表示包络的形状，θl表示任意相位。

考虑到发射信号恒模约束的限制，该问题模型可以表示为

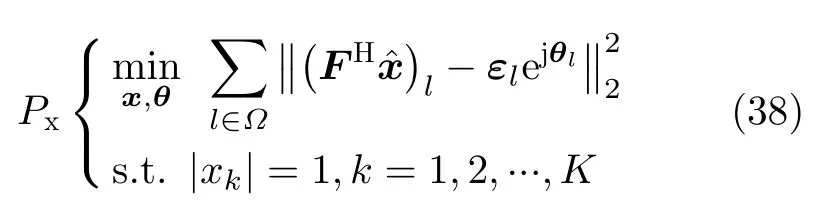
该优化问题Px是恒模约束下的SHAPE算法问题模型[21]，只优化脉内频谱形状的特殊情况，可采用相同的SHAPE算法求解。

4 频域协同波形信号处理方法

雷达发射脉间频率捷变的信号，由于每个脉冲的频率不同，难以在慢时间域进行相参积累[22,23]，为此，本文研究一种基于频率捷变的相参与非相参联合积累方法，其处理流程如图4所示。首先，根据已知的脉冲跳变频率对每个脉冲进行下变频得到基带信号；接着，用已知窄带探测信号对基带回波信号进行匹配滤波，将窄带探测信号从频域分离出来，并提高目标信噪比；然后，对同一频率的多个PRI数据采用FFT实现脉冲间能量相参积累；再对不同频率做非相参积累；最终有效地实现载频变化的脉间频率捷变波形慢时间域积累，输出(距离多普勒)R-D平面。

图4 频域协同波形信号处理方法Fig.4 Frequency domain cooperative waveform signal processing method

4.1 下变频

收/发节点的接收端接收到的第n个周期回波信号可以表示为

其中，回波时延τ=2(R −vt)/c,c=3×108m/s，R表示目标和收/发节点间的初始距离，v表示目标的径向速度，和分别为窄带和宽带接收信号相对于发射信号幅度变化因子，N(t)表示加性高斯白噪声，J(t)表示干扰信号。

在信号处理过程中，本文主要针对窄带回波信号s1,n,z(t −τ)部分进行公式推导和说明。由于第n个周期窄带信号频率fz已知，所以用信号sz(t)=对该周期的回波信号进行混频，得到下变频的基带信号y′(t)。其中，基带回波信号中的窄带信号可以表示为

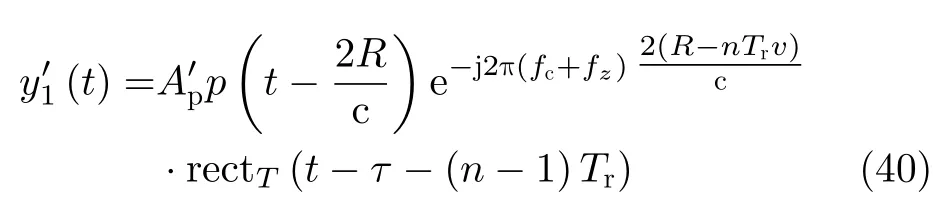
4.2 匹配滤波

基带回波信号和收/发节点发射的基带信号p(t)进行匹配滤波，既减少宽带信号对信号处理的影响，又提高目标信噪比。匹配滤波处理后的窄带回波信号(t)为

其中，⊗表示卷积。

4.3 基于频率捷变的相参与非相参联合积累方法

假设在一个相参处理间隔(Coherent Processing Interval,CPI)内运动目标位于同一个距离分辨单元内，同一频率(fc+fz)的脉冲个数为I，则同一频率的I个PRI数据进行相参积累后得到

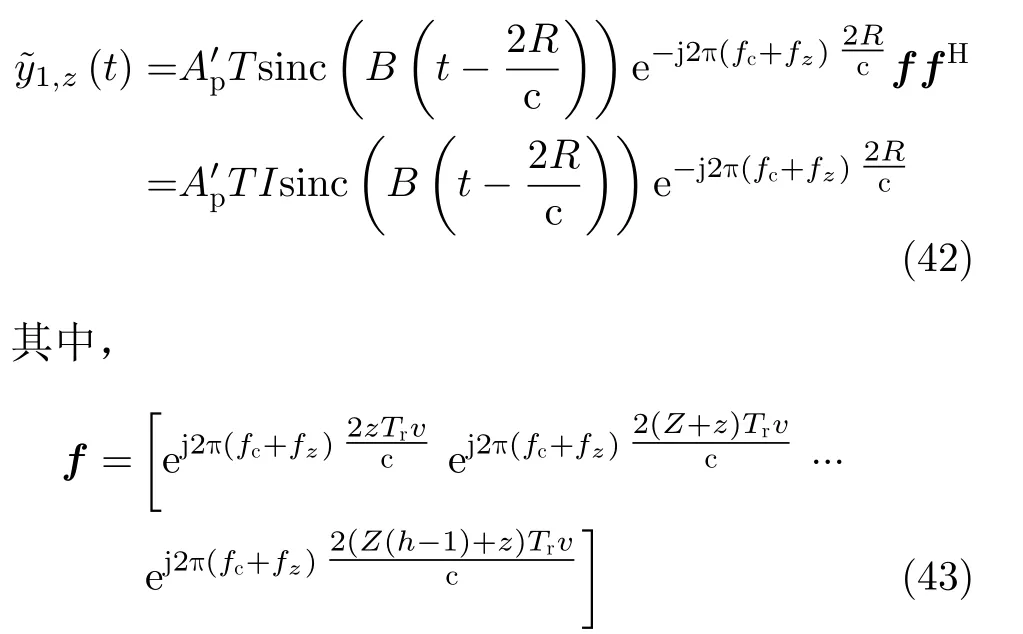
接着，对Z个不同频率做非相参积累，得到

5 仿真实验

5.1 MM-PMM算法性能分析

本小节首先对设计窄带雷达信号的MM-PMM算法性能进行分析。考虑设计恒模波形序列：Ω1=[1 10],ξ=−25 dB(归一化),ςr=ςy=10−4,ρr=5×10−4,ρy=10,γr=γy=10,tmax=2×104,q=20。所设计的波形序列长度分别为M=64,128,256,512。

图5展示了MM-PMM算法设计的窄带雷达信号的局部自相关Ω1区域归一化旁瓣电平随迭代次数变化的曲线。可以看到，对于不同长度的波形序列优化，MM-PMM算法都可以使得Ω1区域归一化自相关旁瓣电平总体保持下降的趋势直到收敛。并且随着波形序列长度的增加，算法优化的自由度升高，得到的Ω1区域归一化旁瓣电平更低。

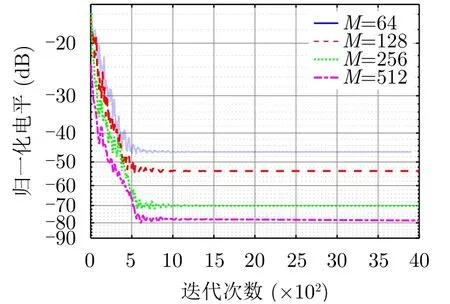
图5 Ω11区域归一化自相关旁瓣电平在不同M下随迭代次数变化的曲线Fig.5 The normalized autocorrelation sidelobe level of Ω1 versus iteration for different M values

接着，考虑到MM-PMM算法中惩罚参数ρr,ρy对收敛性的影响较大，因此针对上述仿真中M=256的情况设置如表1所示不同的惩罚参数分析其对算法收敛性的影响。

表1 惩罚参数设置Tab.1 Simulation parameters of penalty parameters

图6为不同惩罚参数下算法迭代过程中的趋势，当残差∆Rr和∆Ry同时满足退出条件时算法收敛并退出迭代。其中当参数设置为情况1(即ρr=5×10−5和ρy=1)时，算法不收敛，其余3种情况算法收敛。图7反映的是不同惩罚因子设置条件下目标函数的优化程度。从图6和图7中可知，在收敛的情况下，惩罚参数越小，算法迭代次数越多，收敛速度越慢，对目标函数的优化效果越好。根据式(16)可得，当惩罚参数较小时，原目标函数在迭代求解过程中优化比重越大，因此最终的优化效果更好[24]。因此，本文提出的算法应通过上述结论人为调节选择合适的参数。

图6 不同惩罚参数下收敛性分析Fig.6 Convergence analysis under different penalty parameters

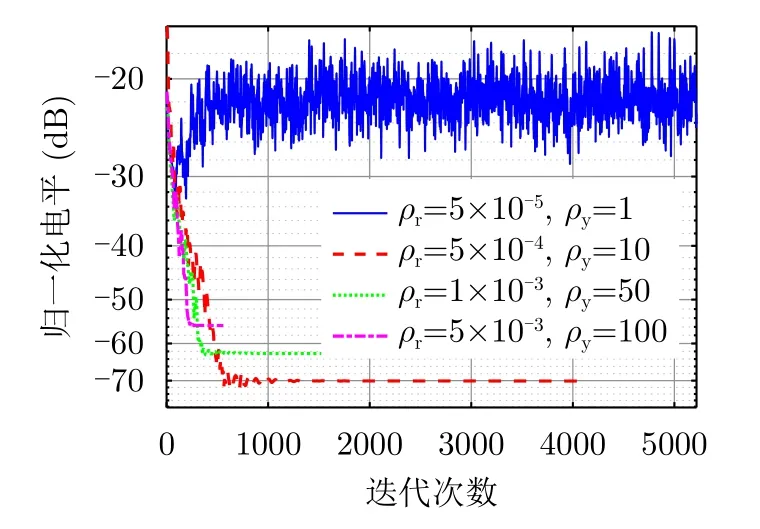
图7 Ω1区域归一化自相关旁瓣电平在不同惩罚因子下随迭代次数变化的曲线Fig.7 The normalized autocorrelation sidelobe level of Ω1 versus iteration for different penalty factor values

5.2 频域协同波形抗干扰性能分析

5.2.1 频域协同发射波形对设计

本节针对设计的频域协同波形进行信号处理分析。假设发射波形参数如表2所示。

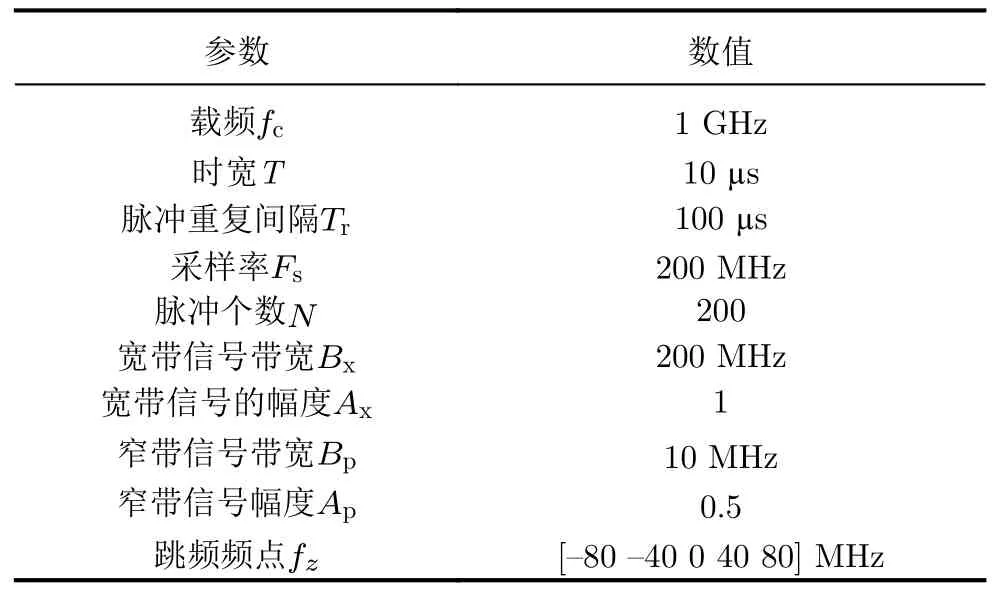
表2 频域协同波形仿真参数Tab.2 Simulation parameters of frequency domain cooperative waveform

根据以上仿真参数设置，设计码字个数为M=BpT=100的窄带雷达信号，考虑全域低旁瓣Ω1=[1 99],ξ=−30 dB(归一化),ςr=ςy=10−4,γr=γy=10,tmax=1×104,q=20。图8 所示为MM-PMM算法优化的窄带雷达信号。图8(a)反映的是恒模序列的时域波形，图8(b)反映的是自相关特性。从图8(b)可以看出自相关旁瓣区域归一化电平达到–30 dB，具有良好的目标检测性能。

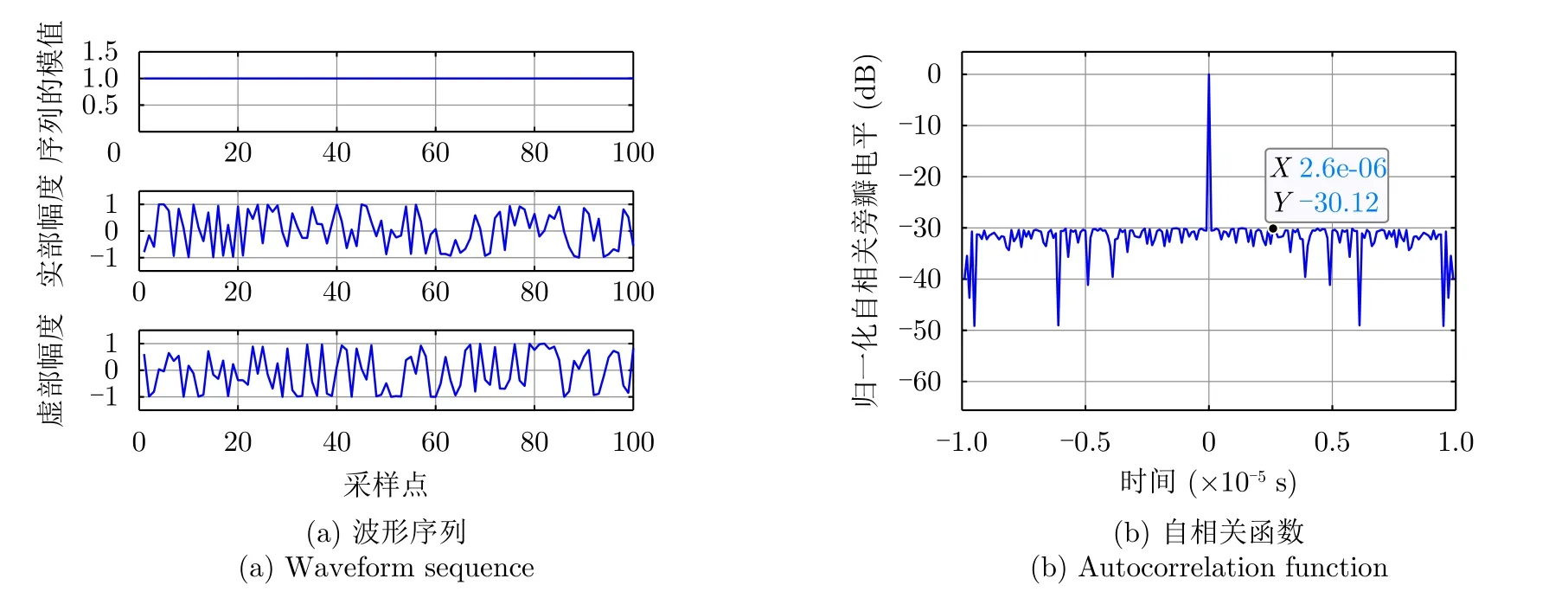
图8 窄带探测信号性质Fig.8 The narrowband detection signal properties

根据跳频频点的参数设置设计5个宽带信号，每个宽带信号的阻带区域Ω分别为[–90–70] MHz,[–50–30] MHz,[–10 10] MHz,[30 50] MHz和[70 90] MHz。阻带区域归一化电平设置为εl=−70 dB。图9反映的即为设计的5个宽带掩护信号的归一化PSD。图10(a)展示了脉间跳频的窄带探测信号和宽带掩护信号的对应关系。从图10(b)可以看出频域协同波形形成的发射信号S(t)PSD在整个带宽B=200 MHz内相对平坦，具有低截获特性。发射节点发射的宽带信号有效掩护窄带探测信号。

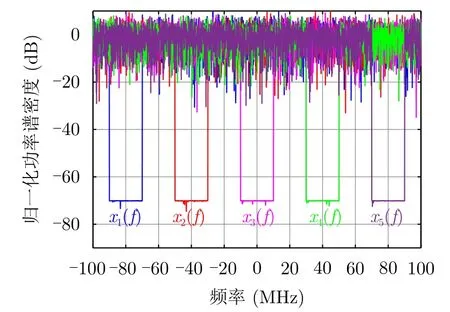
图9 宽带掩护信号功率谱密度Fig.9 The power spectral density of wideband cover signal

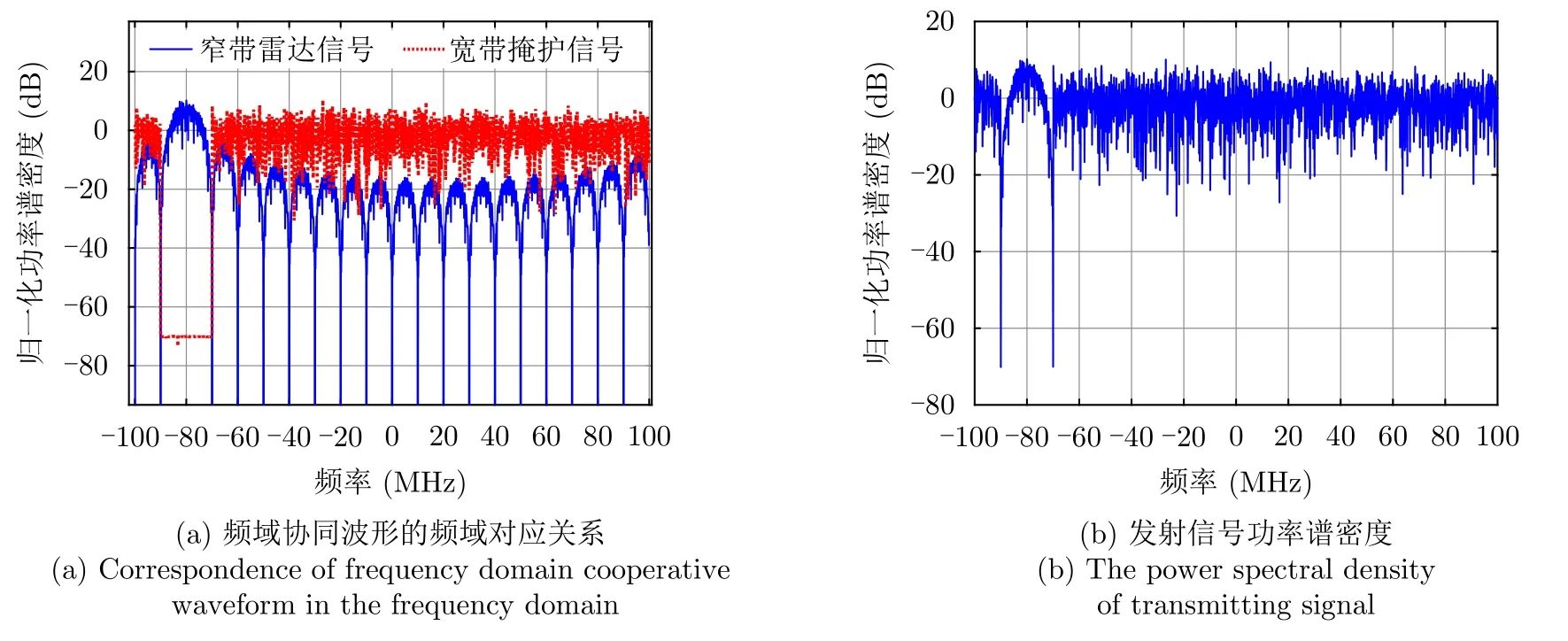
图10 频域协同发射信号功率谱密度Fig.10 The power spectral density of frequency domain cooperative waveform pair

5.2.2 抗噪声调频干扰性能分析

考虑如下形式的噪声调频干扰信号[25]JNFM(t)：

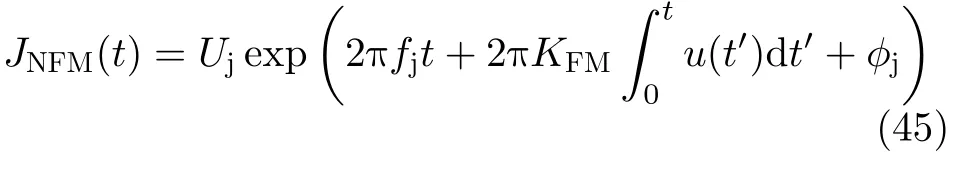
其中，调制噪声u(t)是均值为0、方差为σ2、带宽为∆F的带限高斯白噪声，ϕj为[0,2π)均匀分布的随机变量，且与u(t)相互独立，Uj,fj和KFM分别为干扰信号幅度、载频和调频斜率。

当干扰机截获到频域协同信号时，干扰机从信号中识别出真实雷达窄带信号的频率和带宽较为困难，将发射fj=fc、等效带宽∆B=Bx=200 MHz的宽带噪声调频压制干扰信号；当只发射窄带跳频雷达信号(没有宽带掩护信号)时，干扰机易于识别出雷达信号频率和带宽，将发射与跳频脉冲对应频率fj=fc+fz,∆B=Bp=10 MHz的窄带噪声调频压制干扰信号。为验证频域波形抗噪声调频干扰的性能，仿真对比上述两种情况，其他场景参数如表3所示。

表3 抗干扰场景参数Tab.3 Simulation parameters of anti-interference scenes

图11所示在噪声调频干扰下分别为窄带雷达跳频信号和频域协同信号回波信号处理R-D图。从图中可以看出，经过信号处理后，频域协同信号回波中可以检测到两个目标，但是窄带雷达跳频回波信号经过信号处理后R-D图中旁瓣较高，不易检测出两个目标。这是因为发射频域协同波形时，敌方截获机无法从我方发射信号中提取到有效的窄带跳频信号，只能发射宽带噪声调频信号对我方雷达进行干扰。因此，在我方收/发节点的接收端信号处理过程中，宽带干扰信号能量分散在整个带宽内，对我方收/发节点目标检测影响较小。

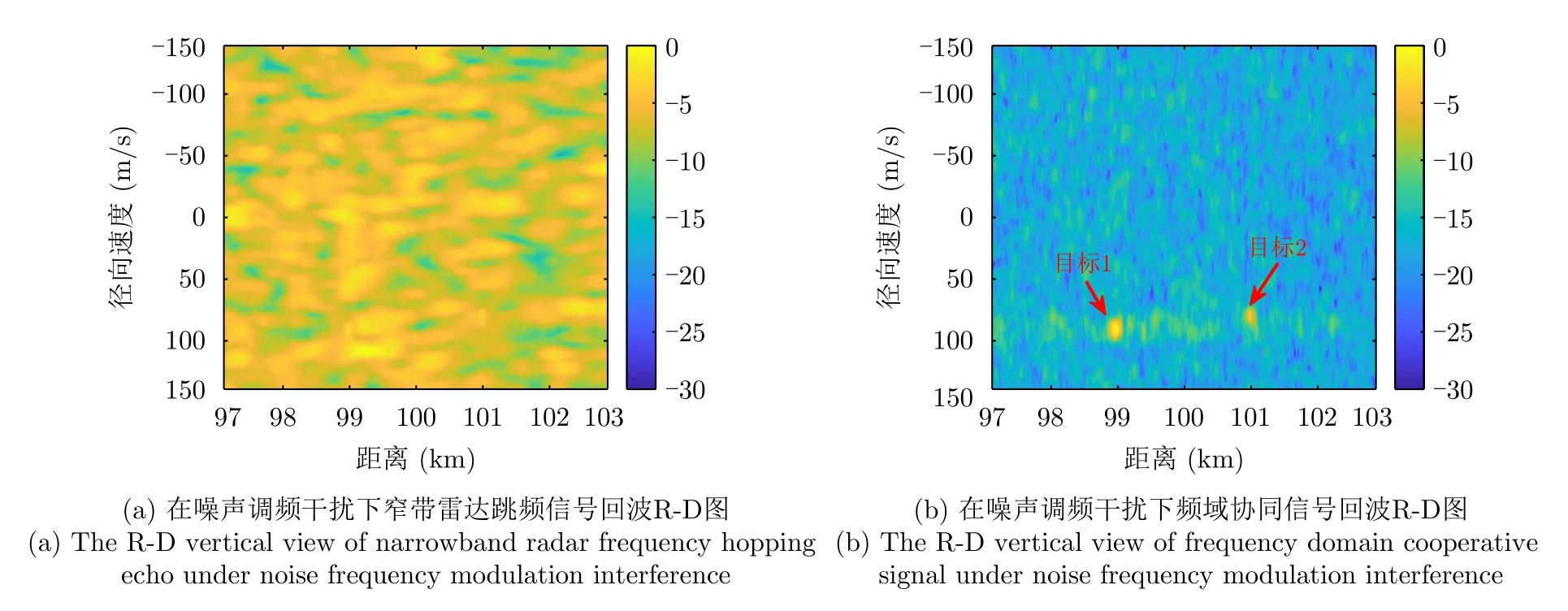
图11 抗噪声调频干扰R-D图对比Fig.11 The R-D diagram comparison of anti-noise frequency modulation interference effect

5.2.3 抗噪声调频和灵巧组合干扰性能分析

考虑如下形式的组合干扰信号：

其中，JNFM(t)表示噪声调频干扰，JSNJ1(t),JSNJ2(t)表示两个参数不同的灵巧噪声信号[26]。本文所采用的灵巧噪声信号通过窄带噪声乘积调制雷达发射信号并增加随机相位产生，其具体表达式可以写为

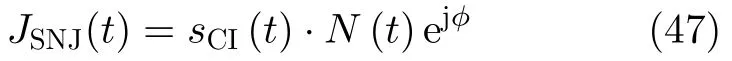
其中，ϕ为随机相位，N(t)为噪声信号，本节仿真中采用噪声调频信号N(t)=JNFM(t)，sCI(t)表示根据雷达发射信号得到的切片-重构信号，具体表达式为

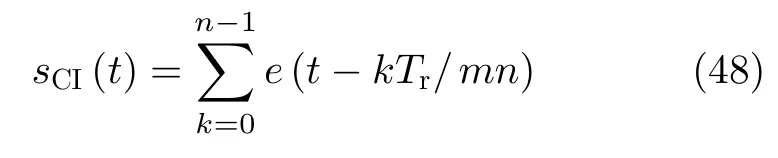
图12 切片转发信号产生原理Fig.12 Generation principle of chopping-interleaving

为验证频域波形抗组合干扰的性能，对比窄带雷达跳频信号，其他场景参数如表4所示。

表4 抗干扰场景参数Tab.4 Simulation parameters of anti-interference scenes

图13所示在噪声调频和灵巧组合干扰下分别为窄带雷达跳频信号和频域协同信号回波信号处理R-D图。从图13(a)中可以看出窄带雷达跳频信号回波经信号处理后不易检测出真实目标，而频域协同信号回波经信号处理后能够在组合干扰的影响下从图13(b)R-D中检测出真实的目标信息。因此，本文提出的频域协同波形方法能够抗3种不同干扰的组合干扰。

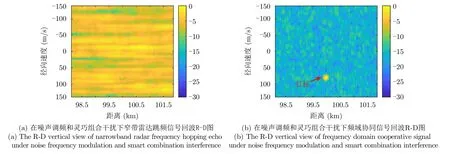
图13 抗噪声调频和灵巧组合干扰R-D图对比Fig.13 The R-D diagram comparison of anti-noise frequency modulation and smart combination interference effect

6 结束语

针对现有单部雷达波形设计方法很难满足日益复杂的电磁环境以及多节点协同作战中雷达抗干扰性能不佳的问题，本文提出一种基于两部短基线节点的频域协同波形设计方法。其中，针对窄带探测信号，本文提出一种基于MM-PMM算法的局部自相关电平优化波形设计方法，同时考虑恒模约束；针对宽带掩护信号，考虑设计对应的避开窄带探测信号频段的宽带频谱置零信号，实现两者的频域协同，从而提升雷达低截获和抗干扰能力。仿真结果表明，针对多种抗干扰的应用场景，本文提出的频域协同波形的方法能够在隐蔽真实雷达带宽的情况下提升目标的检测性能。

为了进一步完善多节点频域协同波形设计，在后续研究过程中，我们一方面将考虑对掩护信号能量的利用，提升信号的利用率；另一方面将考虑时频域联合协同波形设计，在隐蔽雷达探测信号的同时进一步提升目标检测性能。