机载雷达脉间波形参数伪随机跳变技术

崔国龙 樊涛 孔昱凯 余显祥 沙明辉 孔令讲

①(电子科技大学信息与通信工程学院 成都 611731)

②(北京无线电测量研究所 北京 100854)

1 引言

传统机载脉冲多普勒(Pulse Doppler,PD)雷达在相参处理间隔(Coherent Processing Interval,CPI)内发射脉间参数固定的脉冲串信号，在下视探测回波中通常混有分布范围广且强度大的距离(速度)模糊的地(海)杂波，严重影响了微弱目标探测性能。另外，由于机载雷达脉间波形参数确定且周期重复，易被敌方截获分选和识别，进而面临被干扰与打击的风险，降低了电子对抗环境下机载雷达的生存概率[1]。因此，强杂波与干扰一直是机载雷达探测面临的主要挑战。

目前，机载雷达抗杂波与干扰手段主要聚焦于接收处理端，典型技术包括动目标指示、空时二维自适应处理和时频域对消等方法[1,2]。然而，该类技术并未充分释放机载雷达发射端“主动”对抗的能力，难以应对复杂电磁环境下的强杂波与强干扰。机载雷达波形设计技术通过优化理论重新配置发射波形相位、时序、频率等多域参数，扩大杂波/干扰与目标在多域上的差异性，提升杂波与干扰抑制能力。因其发挥了机载雷达发射端“主动”特性，已受到国内外学者的大量关注。

现有机载雷达波形设计主要分为脉内波形和脉间波形两类。其中，脉内波形设计主要通过对子脉冲幅度与相位的设计，实现对波形的自(互)相关函数旁瓣或者模糊函数旁瓣能量的重新分配，以提升微弱目标探测能力；脉间波形设计是指优化配置脉冲间发射时序、载频、幅度和相位等脉间参数，实现对慢时间模糊函数[3]、慢时间自/互相关函数[4]以及多普勒域旁瓣能量[5]的重新分配，以提高机载雷达杂波/干扰抑制与动目标检测的能力。因其与模糊杂波和干扰(特别是慢转发干扰)存在强耦合特性，脉间波形捷变相比脉内波形设计具有更多的抗模糊杂波和干扰的自由度，也是机载雷达设计重要考虑的因素。

传统机载雷达脉间波形参数大多采用固定模式，包括高重频、中重频和低重频等[2]，其存在最大无模糊距离与最大无模糊速度间相互耦合、目标真实信息难测量、折叠杂波难抑制和抗分选识别能力差等缺点。近年来，得益于任意波形产生器等技术的大力发展，机载脉间波形参数捷变受到了广泛关注，其主要通过对脉间初相、脉冲重复间隔(Pulse Repetition Interval,PRI)等脉间参数伪随机跳变，应对传统机载雷达脉间参数重复单一、灵活性差所导致的模糊杂波与干扰问题[6–11]。例如，文献[12–19]通过优化设计雷达脉间波形初相，在保证目标信号相参积累的前提下最小化干扰处理增益，有效地抑制了速度或距离欺骗干扰。也有相关研究通过联合设计脉间幅相[20,21]、脉间频相[22]或脉内脉间相位[23]等多维参数，进一步提升了雷达抗干扰反杂波能力。此外，文献[24–29]还充分发挥了发射和接收联合处理的优势，通过联合设计脉间幅相等参数和接收滤波器，扩大目标与杂波间多维的差异，从而实现对杂波/模糊杂波的有效抑制。为了解决中高重频体制距离速度模糊难以兼顾的技术瓶颈，文献[30]提出了一种非均匀PRI波形(脉冲间的发射间隔在一个CPI内非均匀跳变)，该波形无距离速度模糊，且具备杂波谱重塑和抗截获分选的能力[31]。

综上可知，面向复杂地理与电子对抗环境，机载雷达波形设计在抗杂波与反干扰展现出重要的潜力，其设计理论也经历：(1)从脉内波形向脉间波形设计技术发展；(2)从参数固定向参数随机跳变发展；(3)从单/低维度向多域高维度波形设计发展。故本文仍聚焦于机载雷达脉间波形设计技术，着重分析阐述了脉间波形在抗杂波/干扰方面的优势，主要包含：(1)无模糊测速测距能力：脉间波形的PRI和初相等参数伪随机跳变，以及非均匀相参处理，实现对目标距离和速度的无模糊测量。(2)杂波功率谱重构能力：脉间波形的PRI、初相和幅度等调制参数的优化设计，控制杂波谱形状，解决强折叠杂波对弱目标探测的影响。(3)抗分选与抗干扰能力：脉间波形参数伪随机改变，增加波形的复杂度与不确定性，增大敌方截获机分选识别的难度，同时提升了慢转发干扰抑制能力。具体而言，本文通过脉间PRI和初相等参数伪随机跳变，提出了一种基于距离门对齐的非均匀相参处理方法，保证了目标的相参积累能力，有效解决了现有相参方法存在多普勒旁瓣高[32]、信噪比依赖较强[33,34]等问题。在此基础上，研究分析了其反杂波和抗干扰能力。

本文结构安排如下：第2节主要介绍机载雷达脉间波形参数伪随机跳变回波的信号模型；第3节给出一种面向脉间波形参数伪随机跳变信号的非参数化相参处理方法并分析了其抗干扰优势；第4节重点分析脉间波形参数伪随机跳变信号的杂波特性和抗杂波方法；第5节总结全文。

2 机载雷达脉间波形参数伪随机跳变回波模型

如图1所示，假设载机的高度为H且沿着x轴方向以速度V匀速飞行，机载相控阵雷达波束主瓣方位角和俯仰角指向(θ0,φ0)。图2(b)展示了机载相控阵雷达在一个相参处理间隔tCPI内发射M个脉间波形参数伪随机跳变的相参脉冲串，即每个脉冲的基带信号s(t)相同，但相比于传统波形脉冲初始相位和PRI等脉间参数均匀无变化(如图2(a)所示)，其脉冲初始相位不同，且PRI是非均匀的，具体的基带波形数学表达式为

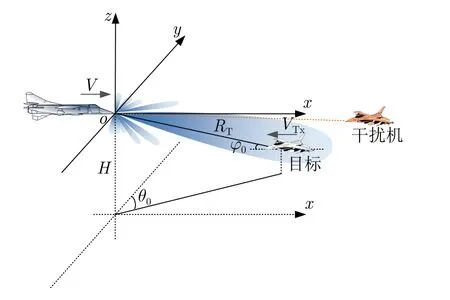
图1 机载雷达探测场景示意图Fig.1 Schematic diagram of airborne radar detection scene

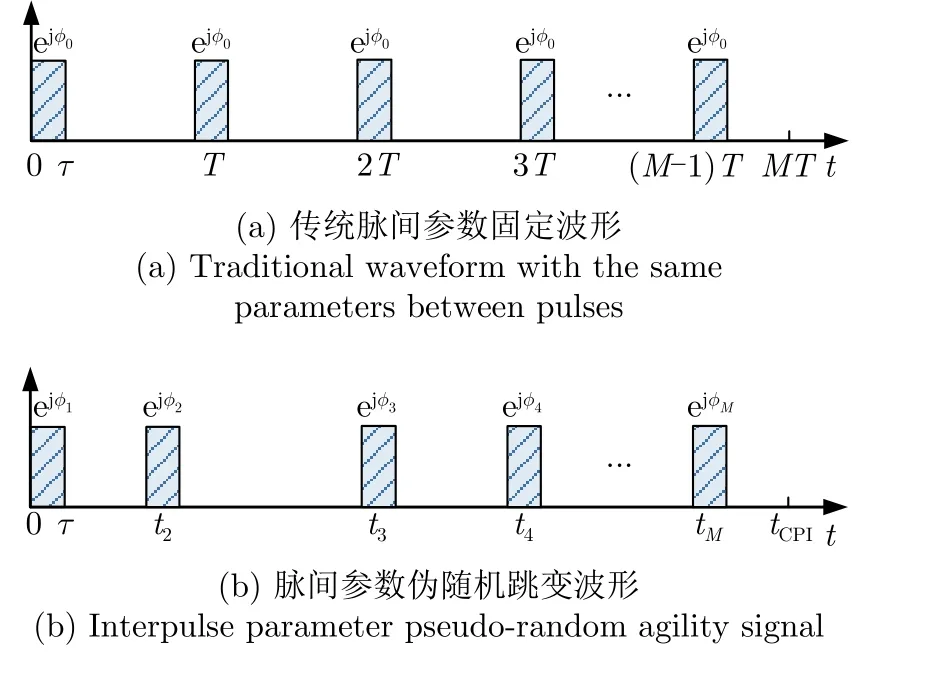
图2 发射波形示意图Fig.2 Diagrams of the transmitted waveforms

其中，ϕm和tm分别为第m个脉冲的初相和发射时刻，τ为基带脉冲宽度。不失一般性，令t1=0,tCPI=MT

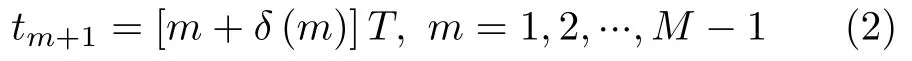
其中，T是固定重频波形的PRI，δ(m)是 (−µ,µ)上的均匀分布，即δ(m)∼U(−µ,µ),µ∈[0,0.5−τ/T]；需要说明的是，当µ=0时，式(2)退化为固定重频波形发射时刻的表达式。s(t)可以为线性调频、频率编码或相位编码等任意调制波形。u(t)是矩形窗函数

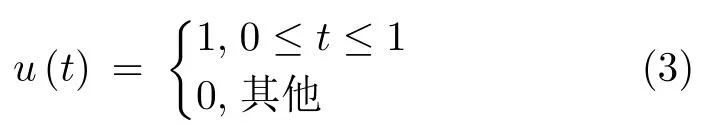
假设在机载雷达主瓣波束照射范围内，存在一个径向距离为RT，径向速度为VT的匀速飞行点目标，其回波可写为

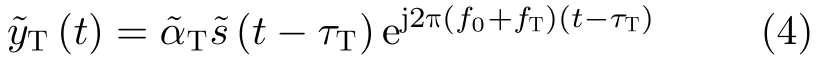
其中，f0是雷达载频，是与相对距离、天线增益和发射功率有关的常复数幅度因子，τT=2RT/c表示双程传播时延，c为光速，fT=2VT/λ是目标的多普勒频移，λ为波长。经过下变频处理后，目标回波可以重写为

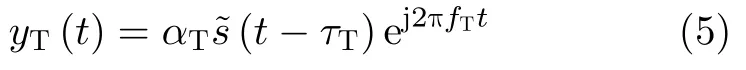
其中，αT包含了，目标RCS以及雷达方程中所引入的其他常数项。

假设机载雷达主瓣波束内存在一个干扰机，如图1所示。该干扰机完全截获到雷达基带调制波形s(t)，并以固定脉冲间隔TJ，不断地向机载雷达实施Q个距离速度联合欺骗假目标干扰，则经过下变频后基带干扰回波为

最终，机载雷达回波可以表示为

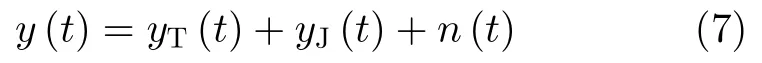
其中，n(t)为零均值、方差为的加性高斯白噪声。

3 脉间波形参数伪随机跳变相参处理技术

脉间发射时刻的伪随机捷变特性使得传统脉冲多普勒处理技术已不再适用。本文基于距离门对齐思想，提出了一种脉间波形参数伪随机跳变的相参处理方法，处理流程框图如图3所示。

图3 脉间波形参数伪随机跳变信号相参处理流程Fig.3 Coherent processing flow of interpulse parameter pseudo-random agility signal

首先，基于每个脉冲的发射时刻，对y(t)执行距离门对齐操作以保证各个脉冲的目标回波在慢时间维度同步并对齐；然后，基于脉间调制的初始相位参数，对慢时间脉间初相进行补偿，保证目标回波在慢时间维度的初相对齐；最后，通过脉间相参处理，实现对参数伪随机跳变波形回波能量的积累。

3.1 距离门对齐处理

距离门对齐主要对雷达回波按照发射脉冲串的时序关系，进行时移重新排列回波信号，实现目标脉冲回波出现在对应的距离门(时延)处[35]。具体而言，根据脉冲的发射时刻，依次将y(t)往左平移tm,m=2,3,...,M，并对移出0时刻的信号做截断处理，形成M路脉冲回波信号，即

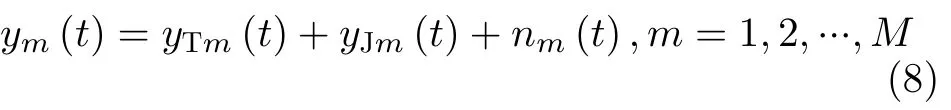
其中，yTm(t)=yT(t+tm),yJm(t)=yJ(t+tm),nm(t)=n(t+tm),m=1,2,...,M。具体地，对齐后的目标信号和干扰信号可以表示为

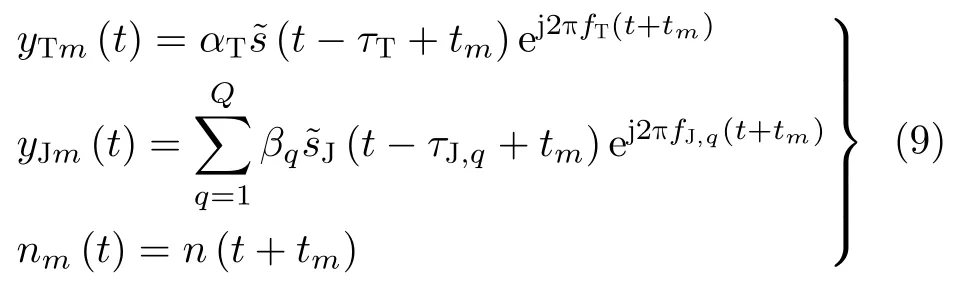
为了直观理解距离门对齐处理技术，图4展示了点目标回波执行距离门对齐处理的示意图，即yT(t)按照发射时序依次向左时移使得目标各个脉冲的回波均位于时延τT处。

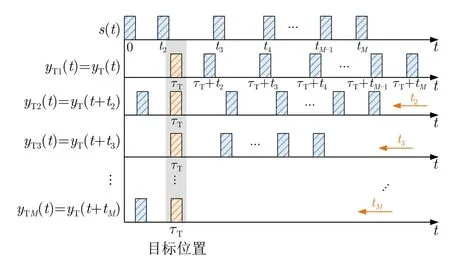
图4 点目标距离门对齐示意图Fig.4 Schematic diagram of point target range alignment

固定重频信号经过距离门对齐处理后，会在各个脉冲时间内均形成对齐的目标回波，因而其无模糊距离受限于PRI持续时间，即c·PRI/2；而脉间参数伪随机跳变波形仅在目标真实时延处形成对齐回波，在其他脉冲时间内无法对齐，因而其最大无模糊距离可认为仅与tCPI有关，即

对于机载雷达而言，相参处理间隔tCPI通常较大，有tCPI≫τT。因此，可以认为脉间参数伪随机跳变波形具备无模糊测距能力。

3.2 脉间初相补偿处理

为了消除脉间波形初始相位跳变的影响，通常需要补偿脉冲回波的初相。在进行距离门对齐后，针对第m路回波数据中所有第m个脉冲的回波，其初始相位已知。因此，可直接进行初相补偿，即

3.3 脉间相参积累处理

利用脉内调制信号s进行匹配滤波，可实现脉内信号的相参积累。由于脉间PRI参数的非均匀特性，可以利用NUDFT技术实现脉间相参积累。然而，传统基于NUDFT技术的相参处理，导致较高的多普勒旁瓣电平。因此，本文提出了一种加权NUDFT技术，以提升多普勒旁瓣抑制的自由度。其主要思想是在NUDFT滤波矩阵基础上增加一个额外的复加权滤波器(w ⊙Γ(l)),l=1,2,...,L，其中Γ(l)表示中心频率为fl的NUDFT滤波器。需要指出的是，当w=[1,1,...,1]T时，该技术退化为基于NUDFT相参积累方法。传统基于FFT技术的相参积累方法计算复杂度为O(Mlog2M)，而加权NUDFT技术主要计算复杂度为O(M2+M)，可在不大幅增加计算复杂度的条件下提升多普勒旁瓣电平抑制能力。

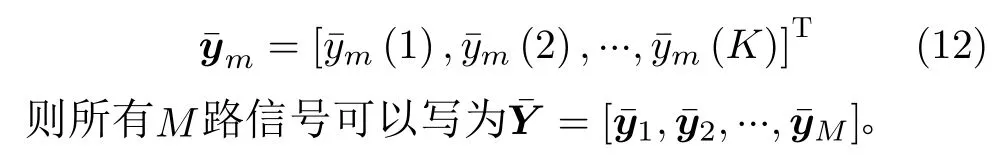
此外，脉内调制信号的离散形式表示为

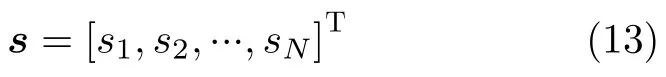
对第k个距离单元的信号执行脉压和NUDFT处理后，第(k,l)个距离-多普勒单元信号的表达式为

对于一组指定的k和fl，g(k,fl)依赖s,w以及p(隐含在中)。因此，在实际中，可以通过设计一组合适的s,w和p，重塑g(k,fl)的形状，提升杂波和干扰抑制能力。

相比于传统固定PRI信号的最大无模糊速度受PRI大小限制，脉间参数伪随机跳变波形的最大不模糊速度与脉冲发射的时间间隔tm −tm−1,m=2,3,...,M有关，文献[36]已经推导出了脉间PRI捷变波形的最大不模糊速度计算公式，表明了脉间参数伪随机跳变波形具备无模糊测速能力。

3.4 点目标相参特性分析

本节利用数值实验对点目标相参积累性能进行了仿真验证。假设机载雷达发射脉冲数M=512，脉内波形s为带宽和脉宽分别为B=5 MHz和τ=2 µs的线性调频信号，脉间发射时刻由µ=0.4,T=20 µs随机产生，脉间初相p为随机相位编码，脉间相参处理端权系数w=[1,1,...,1]T。假设目标相对机载雷达的距离和速度分别是R=120 km和V=500 m/s，定义信噪比SNR为

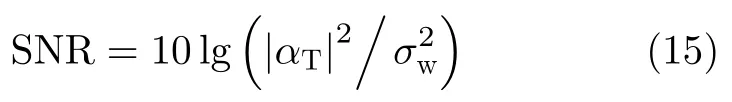
仿真中设置SNR=0 dB。为排除干扰回波对目标相参积累特性的影响，该仿真中考虑无干扰，即βq=0,q=1,2,...,Q。

图5(a)展示了距离门对齐处理后的距离-脉冲二维图。可以看出，在目标真实位置时延τT=2R/c=800 µs处，各脉冲回波实现对齐；在其他时延处，出现了大量的非期望脉冲回波，不利于弱目标的检测。图5(b)给出了目标时延处慢时间回波经过初相补偿处理后的相位曲线，从仿真结果可以看出相位由随机调制变为线性调制，消除了脉间初相跳变对相参处理的影响。

图6给出了脉内波形参数相同情况下，基于NUDFT积累技术的机载雷达脉间参数伪随机跳变波形、低重频(1.25 kHz)、中重频(20 kHz)和高重频(100 kHz)的单目标相参处理结果。通过对比R-D平面可以得出，低、中和高重频距离和速度模糊难以兼顾，难以直接获取目标真实的距离和速度信息；而脉间参数伪随机跳变波形处理后，在目标真实距离120 km和速度500 m/s处相参积累形成检测尖峰。图6(e)和图6(f)分别是脉间参数伪随机跳变波形处理平面在目标速度和距离处的切片图。可以看出，目标速度维的旁瓣基底高于距离维10 dB左右，这是由于脉间PRI随机跳变所导致的多普勒谱泄露。

为了降低NUDFT处理导致的高旁瓣电平，以最大化多普勒维的峰值旁瓣电平为设计准则，在相参处理增益不变的约束下，通过降低主瓣分辨率，优化设计接收加权w，降低旁瓣电平[35]。具体地，假设波形脉间参数与图5保持一致，利用所设计的接收权值处理后，目标速度维结果如图7所示。可以看出，加权NUDFT技术相比传统NUDFT的相参积累方法，其旁瓣电平下降了近–15 dB，且具有“平缓”的旁瓣特性。其次，加权NUDFT技术的主瓣宽度有所展宽。

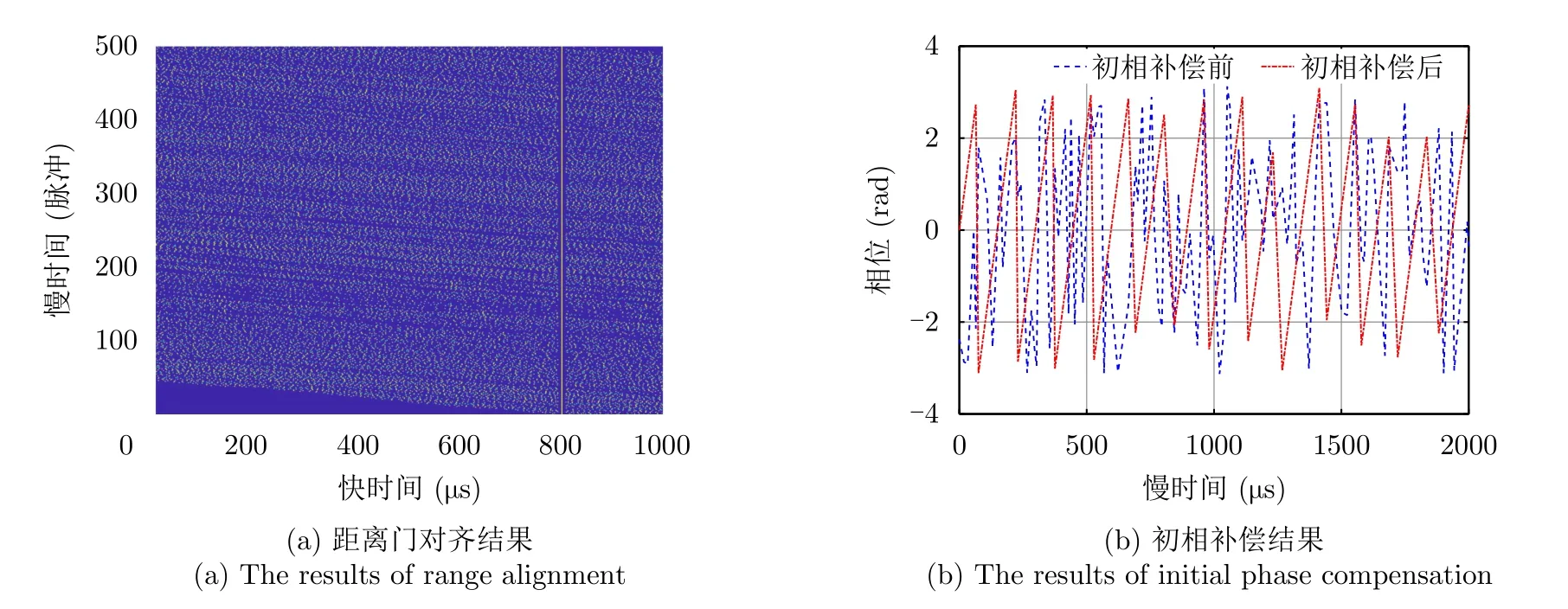
图5 距离门对齐和初相补偿处理结果Fig.5 The results of range alignment and initial phase compensation

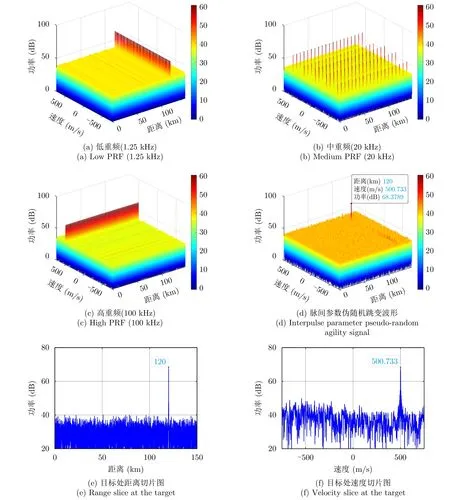
图6 相参积累结果Fig.6 The results of coherent processing

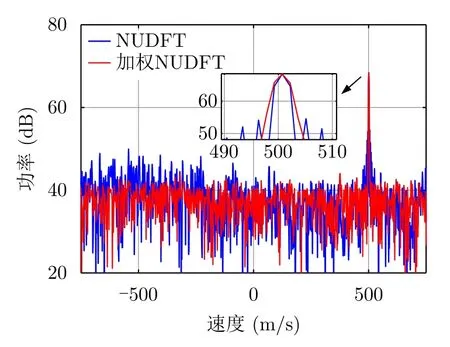
图7 目标速度维结果Fig.7 Target velocity dimension results

3.5 抗干扰性能分析

脉间参数伪随机跳变波形及其相参处理技术具备天然的抗欺骗干扰能力，如图8所示。脉间PRI的伪随机跳变，导致干扰信号的时序关系难以与发射信号脉间时序关系保持一致，在接收端通过时序对其进行相参处理，目标可以获得处理增益，而干扰时序与波形发射时序无法准确对齐，难以获得处理增益，在积累后形成“白化”的效果。

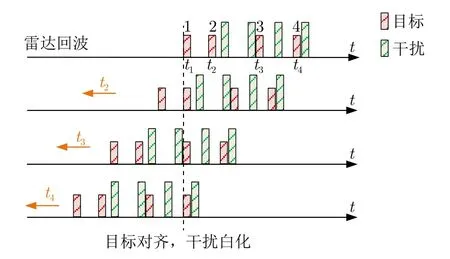
图8 欺骗干扰白化示意图Fig.8 Schematic diagram of deception interference with whitening

定义第q个欺骗干扰的干信比：

假设干扰机以固定脉冲间隔TJ=10 µs，在距离110～130 km和速度400～600 m/s范围内，随机调制了Q=30个假目标，JSRq=3 dB,q=1,2,...,Q。

图9展示了高重频和脉间参数伪随机跳变波形的干扰处理结果，可以看出，传统固定重频易被干扰机识别重频规律，从而在R-D平面内形成密集假目标干扰，影响机载雷达的正常工作；而脉间参数伪随机跳变波形因其脉间PRI和初相的不确定性，使干扰能量被白化至整个距离-速度平面内，无法形成有效的欺骗干扰，同时能保证真实目标能量被有效积累。

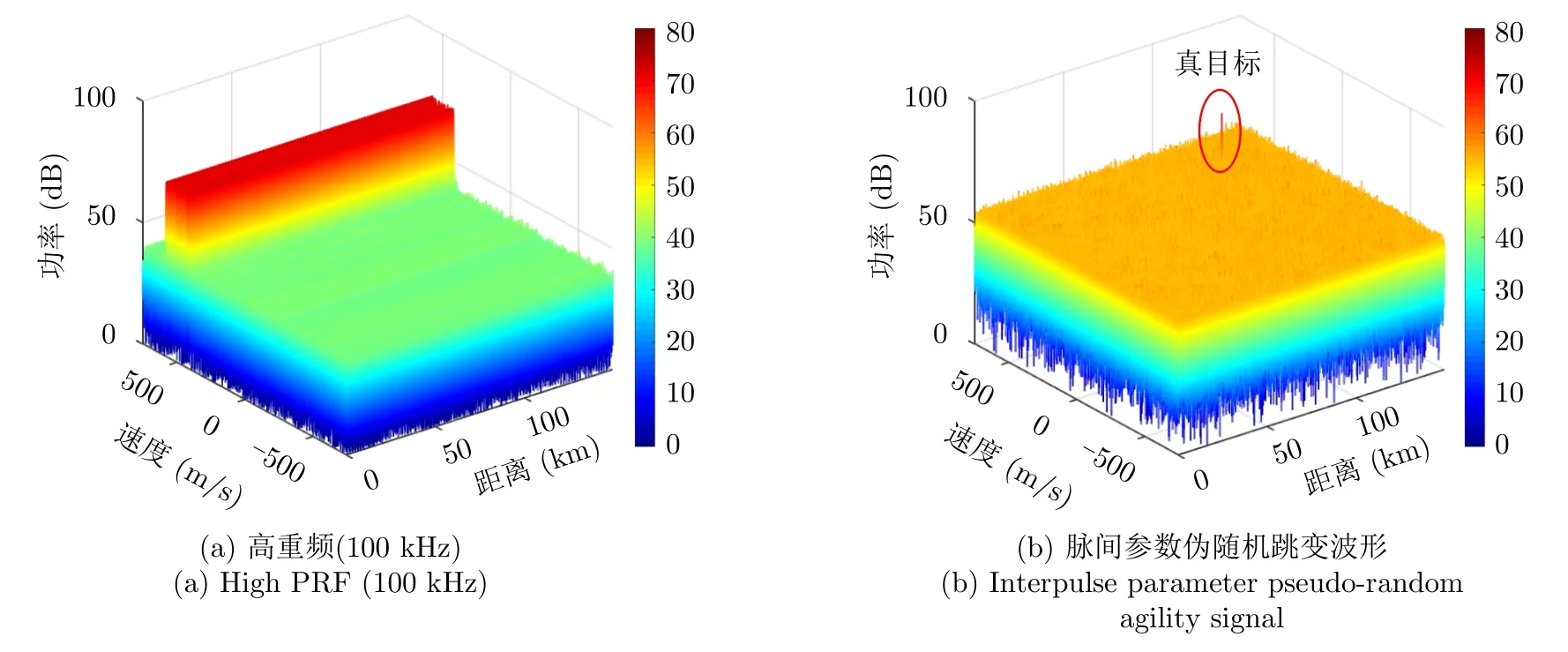
图9 抗干扰效果Fig.9 Anti-interference effect

4 脉间PRI伪随机跳变反杂波技术

脉间PRI随机跳变波形具备无模糊测速测距能力，可重构杂波功率谱形状，使得模糊杂波能量扩散到整个距离-多普勒平面，在反杂波方面展现出一定的潜力。下面，本文将从脉间PRI伪随机跳变波形依赖的机载雷达杂波回波模型出发，分析机载雷达杂波谱特性，并提出一种基于发射和接收滤波器联合优化设计的速度模糊杂波抑制方法，可有效抑制感兴趣区域内的杂波能量。

4.1 脉间PRI跳变下杂波回波模型

将观测地面按照等距离-多普勒环划分为∆R×∆f大小的杂波单元，如图10所示。假设杂波块内的后向散射系数、天线增益、俯仰角、擦地角等都为一常数，且杂波块间的后向散射系数相互独立，不会相互影响，其中∆R表示距离分辨率，∆R′是∆R在地面上的投影。

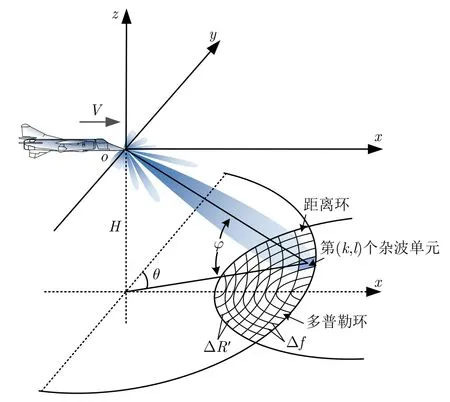
图10 机载雷达杂波单元划分示意图Fig.10 Schematic diagram of airborne radar clutter unit division

假设单位杂波单元面积dA(R,f)对应的方位角和俯仰角分别为θ和φ，则从地面单位杂波面积dA(R,f)反射的平均能量可由式(17)—式(20)计算得到[37]。

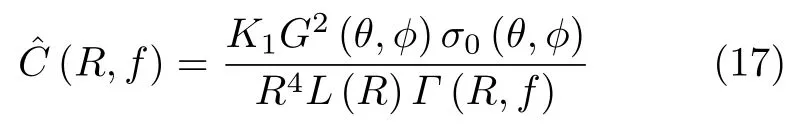
其中，

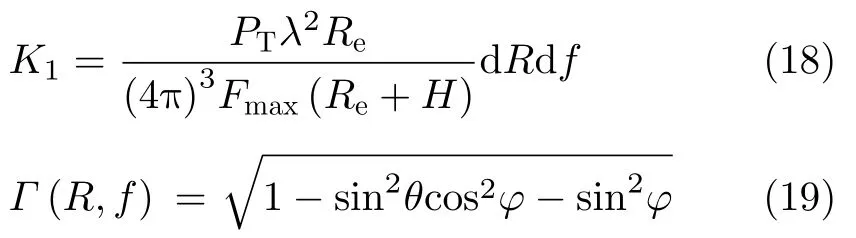
PT是雷达发射功率，L(R)=10αR/5000为损耗因子，其中α是单程损耗系数，G(θ,ϕ)为天线增益，σ0(θ,ϕ)表征地面散射特性，Re为地球半径。Fmax为杂波最大的多普勒频率，其值与载机速度有关，即

将杂波回波建模为多个杂波单元块回波的叠加，可以表示为

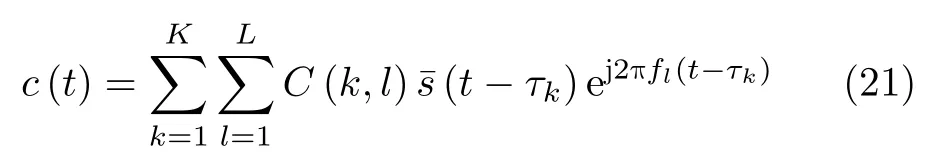
其中，τk和fl分别是第(k,l)个杂波单元的双程时延和多普勒频率，

假设机载雷达发射M=128个脉冲，脉内波形s为随机相位编码信号，脉间发射时序由µ=0.32，T=0.8 ms随机产生，设置w=[1,1,...,1]T，其他参数如表1所示。

表1 杂波仿真参数Tab.1 Clutter simulation parameters

图11给出了低重频(1.25 kHz)和PRI伪随机跳变波形的杂波谱分布图，可以看出，机载雷达发射低重频时主瓣杂波、高度线杂波以及旁瓣杂波均存在严重的速度混叠，不利于目标的检测；而脉间PRI伪随机跳变波形具备无距离速度模糊特性，如图11(b)所示，机载雷达杂波谱无混叠，呈现出典型的高度线杂波、主瓣杂波和旁瓣杂波特性，且具有较大的杂波清晰区，但旁瓣基底较高，不利于弱目标的检测与跟踪。

图11 机载雷达杂波谱Fig.11 Clutter spectrum of airborne radar

4.2 发射-接收联合设计反杂波方法

本节将基于杂波先验知识，联合设计脉内调制波形s和权值滤波器w，抑制感兴趣区域内强杂波能量，从而实现感兴趣区域的目标检测。相关应用场景主要包括如下：

(1) 机载雷达告警-确认模式。假设在告警阶段以高门限检测到一个疑似目标，则在确认阶段可充分利用告警阶段得到的目标和杂波的先验知识波形与接收滤波器的认知设计，并通过高门限检测器确认目标是否真实存在。

(2) 机载雷达单目标跟踪模式。在目标跟踪阶段，单目标进入强杂波区时容易被杂波淹没，从而导致航迹断裂。同时被跟踪目标下一帧的距离和速度信息可初步预测得到，因此我们可以利用其距离-速度的先验信息和误差范围，建立最大化感兴趣区域信干噪比优化问题，从而抑制感兴趣区域内杂波旁瓣能量，确保目标航迹的连续性。

4.2.1 发射-接收联合优化建模

首先R-D平面内局部感兴趣区域定义为

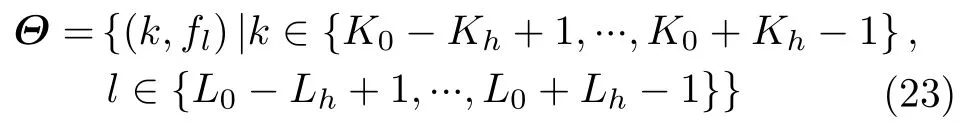
其中，(K0,L0)表示感兴趣区域内的中心距离-多普勒单元，且感兴趣区域大小为NKL=(2Kh −1)(2Lh −1)。

假设感兴趣区域内不存在距离模糊杂波(机载雷达工作于低重频)，距离门对齐处理后，第k个距离单元内的杂波快慢时间数据可表示为[39]

其中，G(s)∈CN×(2N−1)表示脉冲回波混叠矩阵，反映了相邻杂波单元相互串扰的关系，具体可表示为

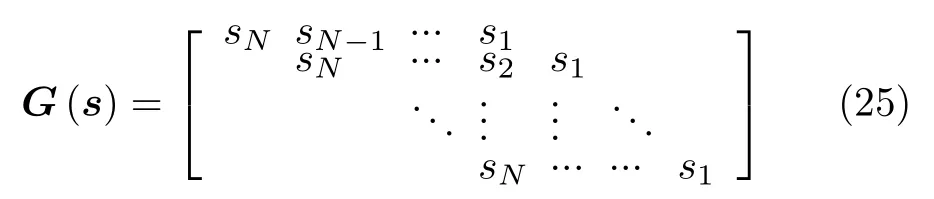
Ck表示第k −(N −1)到第k+(N −1)个距离单元内所有杂波单元复幅度系数的集合，可以表示为

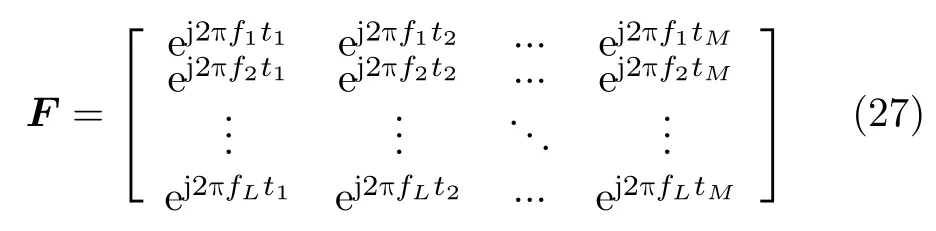
为便于评估感兴趣区域内杂波旁瓣能量大小，定义杂波加权旁瓣电平为

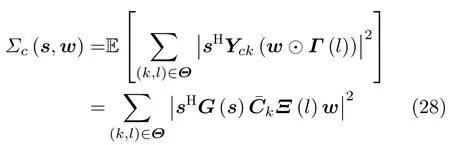
其中，E [·]是期望算子，可由文献[39]附录A计算得到。并定义感兴趣区域内信干噪比(Signal to Interference plus Noise Ratio,SINR)，通过优化设计s和w提升感兴趣区域内潜在目标的检测能力，具体数学表达式是

其中，分子表示位于感兴趣区域Θ内任意点目标的能量，分母表示噪声项和平均杂波加权旁瓣电平之和。与具有类似的物理含义，表示了第个距离单元附近所有目标复幅度系数的集合。在单目标情况下，该矩阵仅有第个元素值为非零。经过代数等价变换，式(29)可以等价表示为

通过在恒模(Constant Modulus Constraint,CMC)和目标峰值增益控制约束下，设计波形与滤波器以最大化SINR，可以有效提升目标探测性能。因此，发射-接收联合优化设计问题可以写为

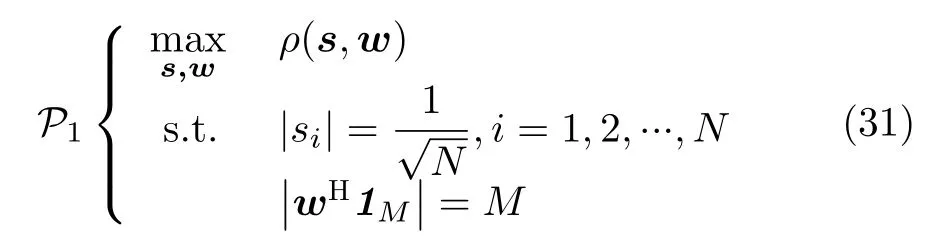
4.2.2 发射-接收联合优化问题求解

P1是一个NP-Hard且非凸的优化问题，无法在一个多项式时间内找到一个最优解。为此，本文通过顺序迭代求解s和w，研究了一种序列贪婪优化(Sequential Greedy Optimization,SGO)算法。其主要思想是首先固定w，求解s；然后固定s，求解w，依次轮换迭代求解直到一定的收敛条件满足。假定s(n−1)和w(n−1)分别表示SGO算法在第(n −1)次迭代的解，则在第n次迭代需求解以下两个优化子问题：

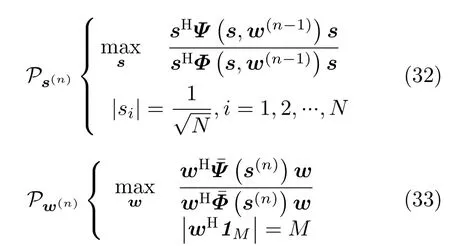
针对子问题Ps(n)，利用基础代数变换，将其等价表示为

最终，通过不断迭代求解s和w，得到P1的次优解sopt和wopt。

4.2.3 仿真分析

假定SGO算法初始化的波形与滤波器分别表示为s(0)和w(0)，则相应的感兴趣区域内的信干噪比与杂噪比分别可表示为

假定感兴趣区域中心点为(K0,L0)=(1228,500)，相应的距离和速度分别设置为46 km和328.5 m/s，CNR0=−60 dB。不失一般性假设一个点目标位于感兴趣区域中心点处，相应的SINR0=−30 dB。另外，为了分析波形约束对SINR性能影响，除了考虑CMC约束，本文还考虑了只有能量约束(Energy Constraint,EC)的情况。

图12展示了不同大小感兴趣区域下的SGO算法收敛曲线，其中(s,w)表示归一化的SINR，相应第n次迭代的值可以计算为

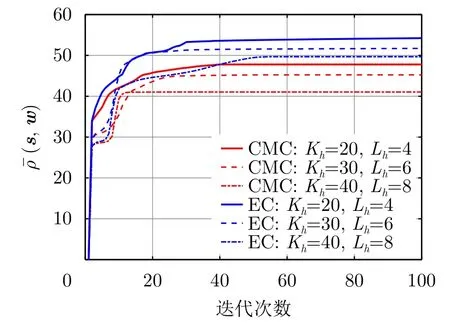
图12 SGO算法收敛曲线Fig.12 Convergence curve of SGO algorithm

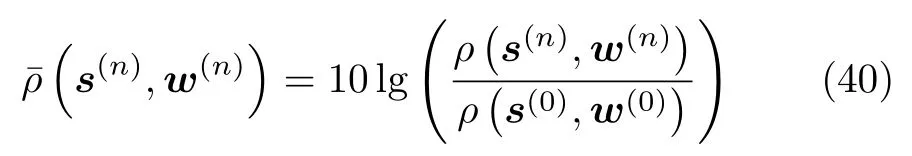
图13给出了CMC约束下，Kh=40,Lh=8时，所设计波形sopt和初始波形s(0)模糊函数的对比结果。可以明显地观察到，sopt是通过牺牲零多普勒处距离主瓣宽度和距离旁瓣电平提升局部区域杂波抑制能力。因此，所设计的波形适应于局部距离多普勒感兴趣区域目标检测，但很难兼顾整个距离多普勒平面内所有目标的检测。若期望所设计波形兼具感兴趣区域外目标的探测能力，未来或设计具有良好互相关电平特性的波形[11]。

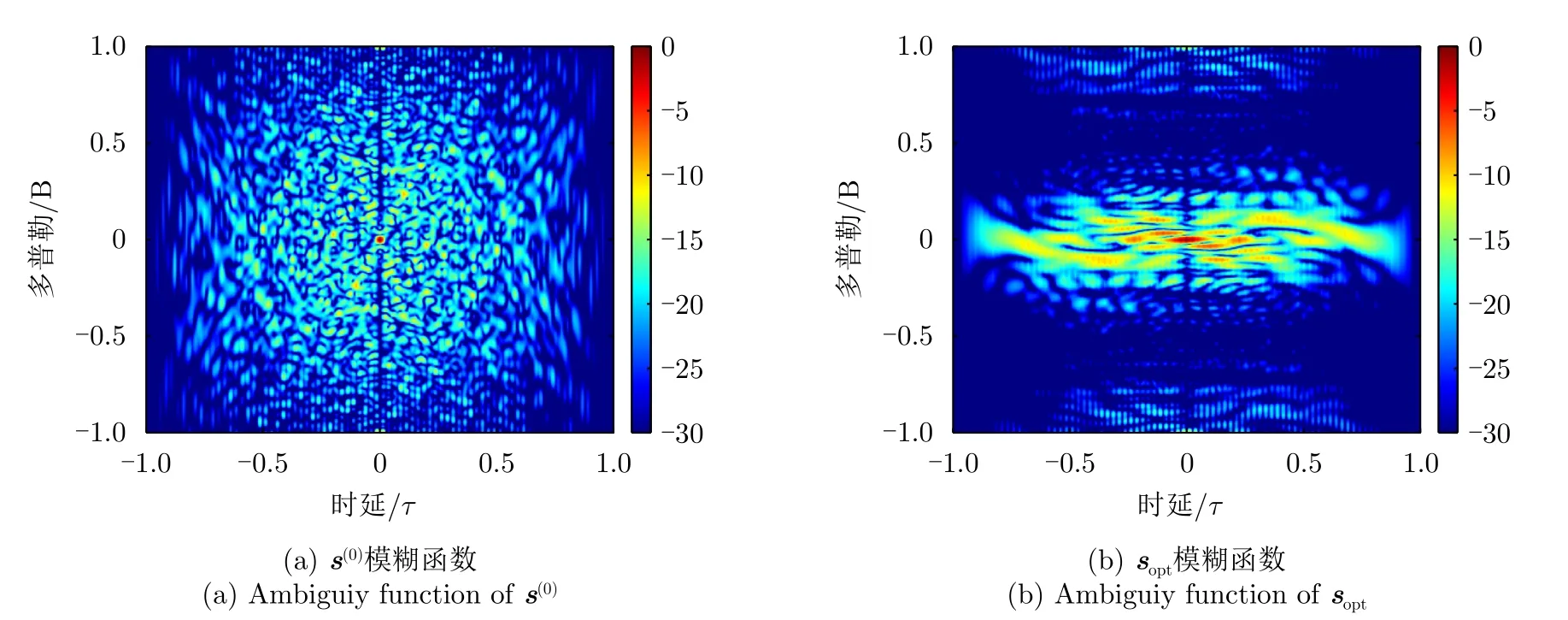
图13 模糊函数比较Fig.13 Contrast of ambiguity function

下面分析在真实目标距离速度偏离感兴趣区域中心的条件下，所设计发射波形和NUDFT加权系数的杂波抑制能力。首先假定目标距离与速度的真实值分别为46.02 km和331.5 m/s，利用跟踪算法得到的距离与速度预测估计值是46.2 km和331.5 m/s。假定载机和杂波相关参数与上节仿真一样，采用在Kh=40,Lh=8条件下，利用SGO设计得到的sopt和wopt作为发射波形和NUDFT的加权系数。图14给出了采用(s(0),w(0))和 (sopt,wopt)处理后的R-D平面及目标处的切片图。结果表明，使用未优化的(s(0),w(0))时，感兴趣区域内的目标完全被杂波淹没，无法检测；而使用(sopt,wopt)，目标在感兴趣区域内清晰可见。此外，观察目标距离和速度切片图可知，目标真实距离和速度附近形成了检测尖峰，SINR相比于未优化时改善了近40 dB，与优化后的改善因子值相符。因此，所提方法在杂波知识和目标先验信息辅助的条件下，能够有效得提升感兴趣区域内的信干噪比，从而提升机载雷达杂波环境下的适应能力。

图14 机载雷达杂波抑制结果Fig.14 The results of airborne radar clutter suppression

5 结束语

本文针对传统机载雷达脉间波形参数重复单一、灵活性差且易被敌方干扰等问题，聚焦于脉间PRI和初相等参数非均匀调制，研究了脉间波形参数伪随机跳变技术，提出了一种基于距离门对齐的非均匀参数相参处理方法，有效保证了目标的相参积累能力，并分析了白化欺骗干扰的能力。在此基础上，建立了基于脉间PRI捷变的机载雷达回波模型，分析了脉间PRI捷变下机载雷达杂波谱特性，并提出了一种基于认知的发射和接收滤波器联合优化设计反杂波方法，有效地提升了感兴趣局部RD区域内的信干噪比。仿真结果表明脉间参数伪随机跳变极大地提升了机载雷达抗干扰和反杂波的自由度，保障了机载雷达在复杂电磁环境下的适应能力，但同时脉间波形参数伪随跳变技术也存在一定的挑战，主要体现在计算量较大、系统设计较为复杂，是未来需要进一步研究和解决的问题。