一种快速抗间歇采样转发干扰波形和滤波器联合设计算法

周凯 何峰 粟毅

(国防科技大学电子科学学院 长沙 410073)

1 引言

随着射频存储转发技术的发展，基于采样转发的相参干扰能够对雷达同时形成压制和欺骗干扰效果[1–4]。间歇采样转发干扰是典型的基于存储转发的相干干扰，其给雷达系统带来严峻挑战[5–9]。为了提高雷达的抗干扰工作性能，抗间歇采样转发干扰技术已经成为目前的研究热点。

目前抗间歇采样转发干扰技术包括接收端信号处理、发射端波形设计和联合波形与滤波器设计方法。时频分析是抑制间歇采样转发干扰的主要接收端信号处理方法[10–12]。文献[10]根据干扰信号和目标回波之间的时频差异实现了对3类典型间歇采样转发干扰的辨识。在此基础上，其提出了一种基于时频域滤波器设计的干扰抑制方法。文献[11]则重点研究了间歇采样转发干扰的识别方法。文献[13]估计了间歇采样转发干扰的关键参数，然后通过干扰信号重构有效抑制了间歇采样转发干扰。然而，现有基于时频处理的方法要求干扰信号和雷达回波在时频域可分辨[11]。当干扰信号产生的假目标和真实目标之间距离不可分时，此类方法的抗干扰性能将显著下降。

第2类方法主要通过设计稀疏多普勒特性波形或脉内正交波形，从而达到抑制间歇采样转发干扰的目的[14–16]。然而，上述方法仅仅考虑了发射端的波形设计，而未在开展波形设计时考虑接收端的滤波器的设计问题。上述方法往往需要在接收端通过分段滤波和滑窗抽取检测等信号处理方法进行干扰识别和抑制。因此，文献[17]提出了一种联合波形和滤波器设计抑制方法，能够在保证脉冲压缩低旁瓣性能的同时有效抑制间歇采样转发干扰。但是其优化算法存在脉冲压缩峰值增益不可控、计算复杂度高和运行时间长等问题。

文献[18]提出一种改进的抗间歇采样转发干扰模型，能有效控制脉冲压缩峰值增益。然而，目标函数近似导致算法收敛速度较慢，且矩阵的乘法计算导致了计算复杂度较高。

为解决上述问题，本文提出一种基于加速主分量最小化的抗间歇采样转发干扰联合波形和滤波器设计算法。本文首先基于罚函数和帕累托最优化原理建立了抗间歇采样转发干扰联合设计的数学优化模型。在此基础上，基于主分量最小化原理推导了迭代过程中波形和滤波器的解析表达式，并通过推导求解过程中矩阵迹的解析表达式，有效避免了矩阵乘法运算，降低了算法计算复杂度。同时，提出了一种基于平方迭代加速方法，进一步加快了算法运行速度。最后，仿真对抗间歇采样转发干扰联合设计数学模型关键参数进行了分析，验证了本文所提算法的可行性。仿真结果表明，在设计波形和滤波器性能基本一致的情况下，本文所提算法比传统方法具有更快的运行速度。并且，本文所提出的方法可解决传统时频处理方法干扰假目标和真实目标距离不可分辨时的抗干扰性能显著恶化问题。

2 联合设计问题模型

本节阐述抗间歇采样转发干扰联合波形和非匹配滤波器设计的问题模型，然后推导得出联合设计的数学模型。

2.1 低脉冲压缩积分旁瓣代价函数

雷达发射波形为相位编码信号，其数学表达式为x=[x1x2...xN]T，其中xn=,ϕn ∈(0,2π]。非匹配滤波器为，其中N表示雷达波形和非匹配滤波器长度。为建立波形和非匹配滤波卷积的矩阵表达式，定义矩阵[17–19]：

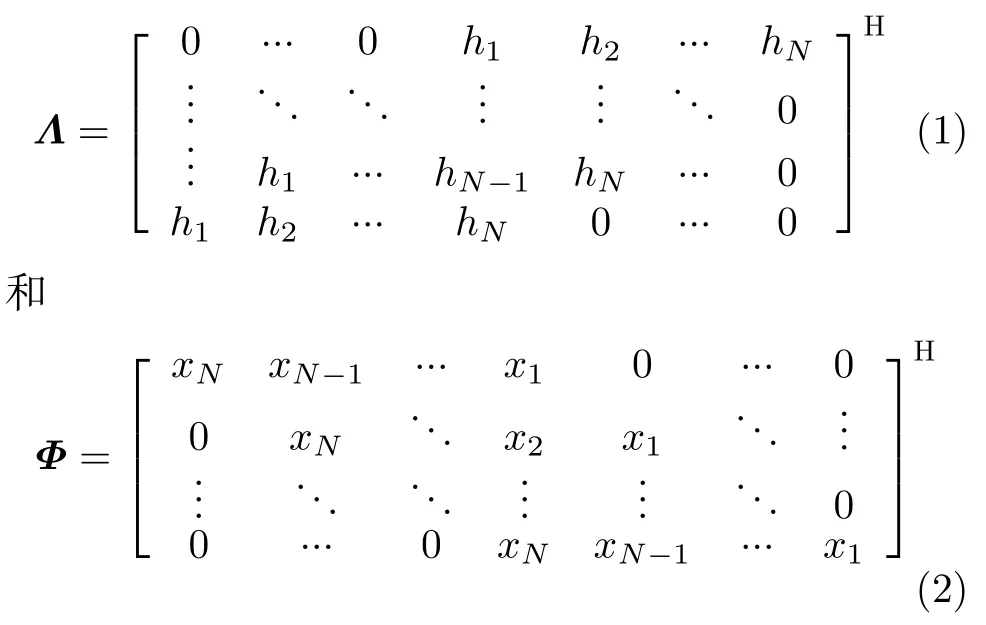
则积分旁瓣能量为xHΛHW Λx或者hHΦHW Φh。其中，矩阵W表示维度为2N–1的对角方阵，除了第N个对角元素等于0之外，其余对角元素为1，且对角元素之外的元素均为0。此外，为约束脉冲压缩峰值，引入目标函数其中bmax表示预设脉冲压缩峰值。基于罚函数方法，抑制积分旁瓣的代价函数为

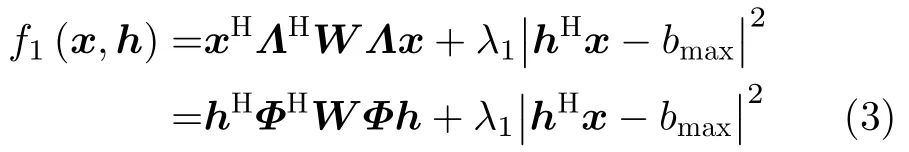
2.2 抑制间歇采样转发干扰代价函数

间歇采样转发干扰是利用数字射频存储技术和数字信号合成技术对雷达发射信号通过间断采样转发，从而对雷达实现干扰。对大时间带宽积脉冲雷达而言，截获到脉冲信号后，高保真度地采样其中一小段信号进行转发，再采样下一段并进行转发，如此收发分时、采样和转发交替工作直至大时宽信号结束。间歇采样信号为矩形包络脉冲串：

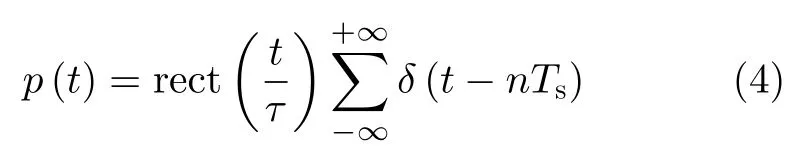
其中，τ表示间歇采样脉冲宽度，Ts表示间歇采样重复周期。间歇采样转发干扰信号为采样信号和雷达发射信号的乘积，即xjam(t)=x(t)p(t)，其中x(t)表示雷达发射信号，xjam(t)表示雷达间歇采样转发干扰信号。间歇采样转发干扰则可以表示为xjam=x ⊙p。其中，p=[p1,p2,...,pN]T表示间歇采样信号的离散序列，⊙表示哈达玛积。同理，构建矩阵

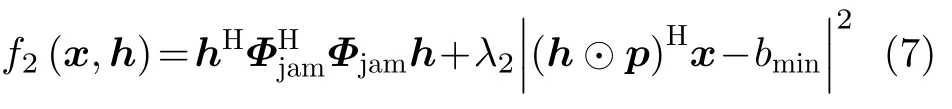
其中，惩罚参数λ2的目的与式(3)类似，其目的是控制目标函数的数值，进而控制设计发射波形对应的间歇采样转发干扰信号非匹配滤波器输出峰值(h ⊙p)Hx。因此，为抑制间歇采样转发干扰峰值，惩罚参数λ2应该取较大的数值[20,21]。利用帕累托优化框架，同时优化上述两个目标函数，则波形恒模和非匹配滤波器能量约束下的联合设计优化问题为

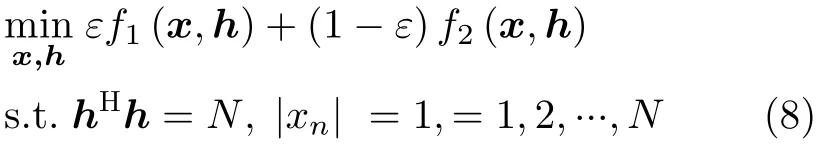
其中，ε表示帕累托权值。由于式(8)约束了接收滤波器能量和波形能量，且最小化目标函数f1(x,h)可实现对波形脉冲压缩峰值hHx的约束，所以本文可有效控制雷达波形的脉冲压缩信号处理增益损耗。此外，占空比决定了算法中设计波形对应的干扰片段的长度，最小化目标函数意味着设计波形中与干扰信号对应的多段信号经过非匹配滤波后将无法获得信号处理增益，进而会导致信号非匹配处理增益损耗。因此，间歇采样转发干扰的占空比越大，则算法设计得到的信号处理增益损耗将会更大，反之亦然。因此，预设信号处理增益峰值bmax时，应充分考虑占空比数值。占空比越大，则预设的bmax应设置较小，以确保能够获得较好的脉冲压缩和抗干扰性能。

3 基于主分量最小化的交替联合设计算法

本节采用基于主分量最小化原理方法分别求取波形和滤波器的最优解，并进一步提出一种加速的交替优化设计方法。

3.1 非匹配滤波器优化

问题(9)是二次约束二次规划问题，由于约束条件是非凸集合，因此难以直接求解。为了求解该问题，先利用主分量最小化原理简化问题。根据主分量最小化方法原理，假设z(l)是第l次迭代得到的最优解，求目标函数的主分量函数u(z,z(l))，使其对任意z∈Ω满足通过优化主分量函数，可得第l+1次的最优解为z(l+1)=进而可得g(z(l+1))≤g(z(l))。相关证明过程可参考文献[21]。

引理1若对任意z ∈Ω满足，则优化问题

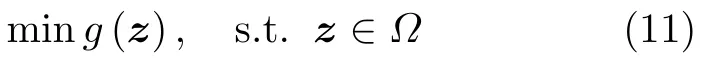
可通过迭代优化其主分量最小化问题获得原非凸问题的最优解：

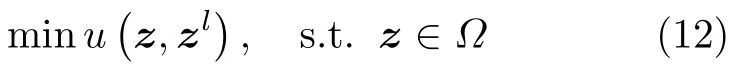
进一步，根据文献[20]中引理1和文献[21]引理1，对任意半正定矩阵L，均有L ≺tr(L)IN。在给定z0情况下，zHLz的主分量最小化函数为

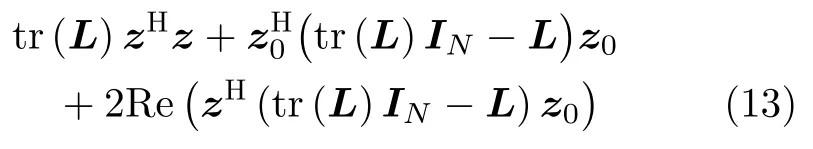
由于文中R(l)满足半正定特性，故hHR(l)h的主分量函数为

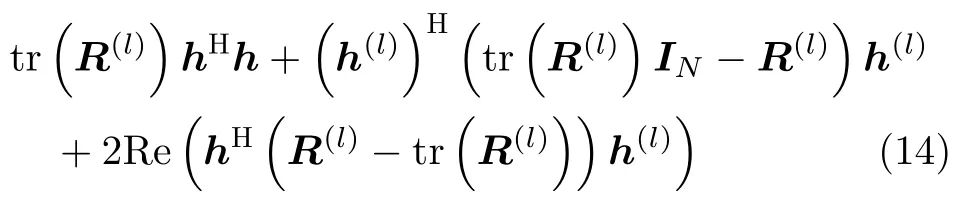
因此，忽略无关常数项和系数后，问题(9)可简化为

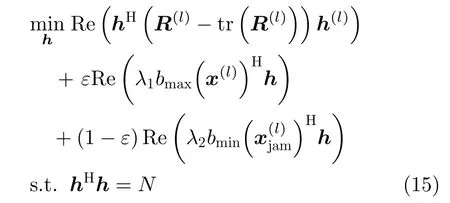
由于式(15)为二次约束的线性规划问题，易得非匹配滤波器表达式为

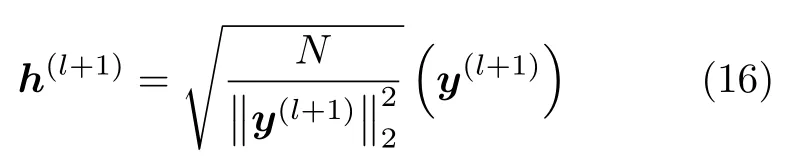
其中

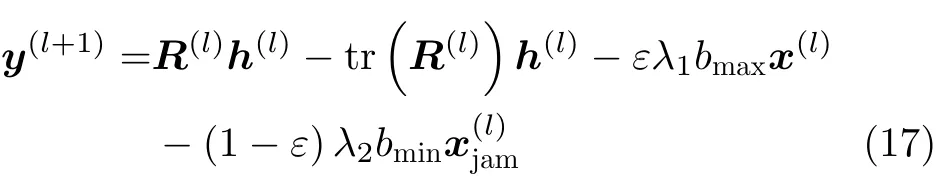
3.2 波形优化

然后，给定非匹配滤波器h(l+1)，将和f2的表达式代入式(8)，波形设计优化问题为

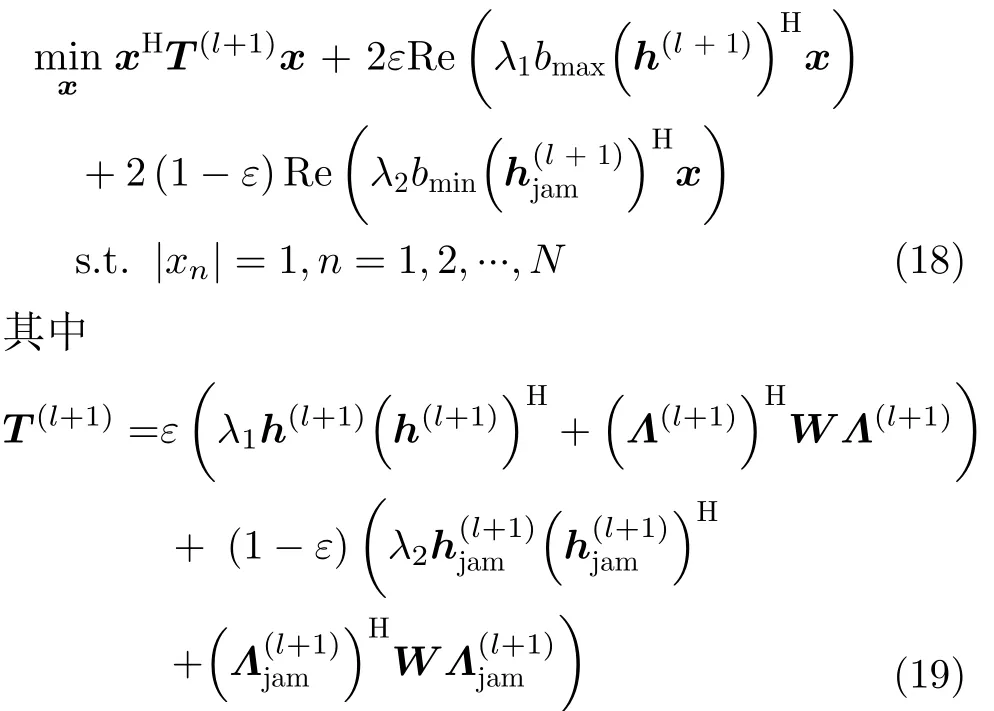
其中，hjam=h ⊙p。因为矩阵T(l+1)为半正定矩阵，所以xHT(l+1)x的主分量函数为

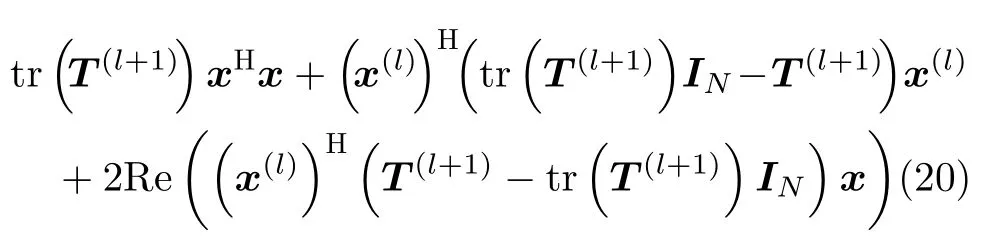
根据引理1，问题(18)可以简化为

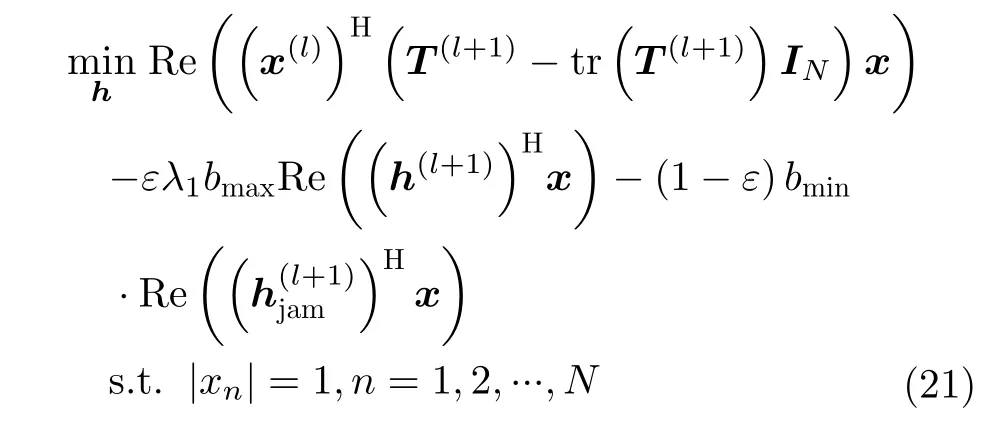
式(21)为恒模约束线性规划问题，很容易得出其解析表达式为

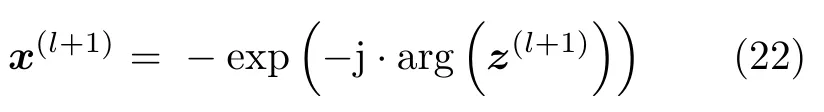
其中

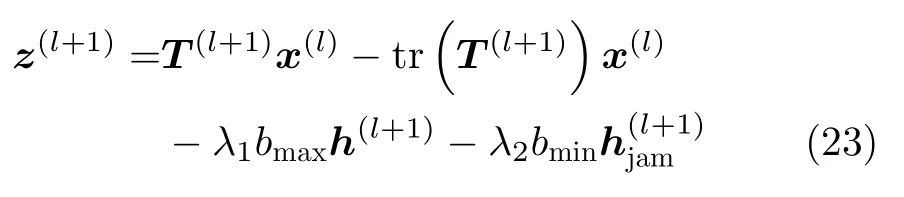
3.3 算法收敛分析

利用主分量最小化方法优化非凸问题的收敛性分析已经有较多的参考文献[20,22–27]。归纳而言，为了证明算法的收敛性能，通常需要证明算法满足以下3个条件：

(1)算法单调递减；

(3) 目标函数的Kurdyka-Lojasiewicz特性[25]。

上述3个条件中，前两个条件是为了保证设计过程中得到的每个子序列均是目标函数的驻点。而第3个条件则是为了证明算法生成的序列是柯西序列，进而证明算法最终收敛。

因此可以证明优化问题中的目标函数是单调递减的。第二，相对误差条件的证明过程是一个标准推导过程，详细的推导可以参考文献[20]的附录B。第三，由于文中的目标函数f(x,h)是可转换为关于波形、滤波器实部和虚部的实函数，因此，其相应的目标函数也可转换为实函数。而另外，所有的实函数均是满足Kurdyka-Lojasiewicz特性的[25]。且由于算法满足单调递减、相对误差条件，故本文所提算法收敛性能得以证明。

3.4 计算复杂度分析

根据式(17)和式(23)可知，更新波形和滤波器的计算复杂度主要集中在其第1项矩阵向量乘积和第2项矩阵迹的计算表达式。其中，将矩阵R(l)表达式代入R(l)h(l)可知，本文式(17)的计算主要涉及矩阵和向量的乘法，因而可避免矩阵与矩阵之间的乘法运算。同理，式(23)的第1项计算复杂度同样也仅来自矩阵和向量之间的乘法。因此，计(算本)文式(17)和式(23)第1项的计算复杂度均为O此外，若直接计算式(17)和式(23)第2项的迹，则需要完全计算出矩阵R(l)和T(l+1)的表达式，其中涉及矩阵之间的乘法，其计算复杂度为O(N3)。因此，若直接计算矩阵R(l)和T(l+1)，算法的计算复杂度将为为了避免计算矩阵R(l)和T(l+1)的迹引入的复杂度，本文进一步推导上述矩阵R(l)和T(l+1)的解析表达式。首先提出下述引理。

引理2由于波形和滤波器均满足能量约束，因此矩阵R(l)和T(l+1)的迹满足

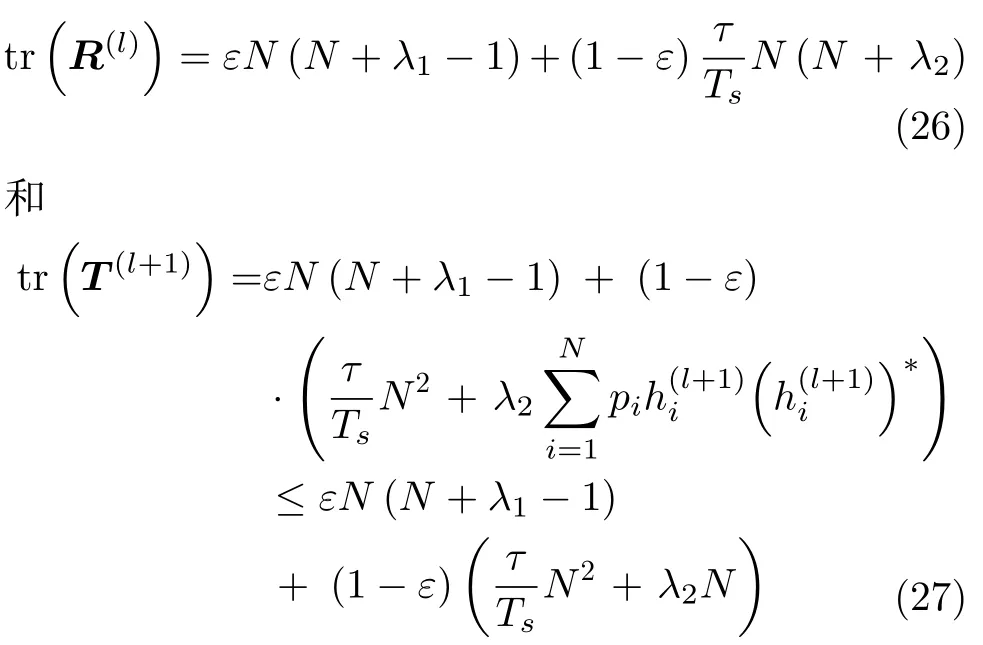
证明：首先，根据矩阵R(l)的定义和矩阵迹的计算引理tr(A+B)=tr(A)+tr(B)和tr(AB)=tr(BA)，可得

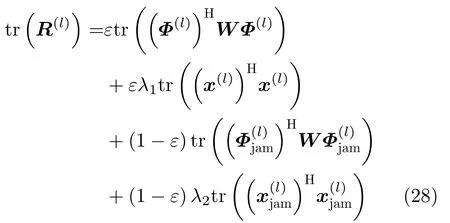
分别合并式(33)的前两项和后两项即可以得到式(26)所述的表达式。矩阵T(l+1)前3项的迹推导过程与矩阵R(l)的迹计算过程一样，且计算结果相等，此处不再赘述。其最后一项中，由于下式满足

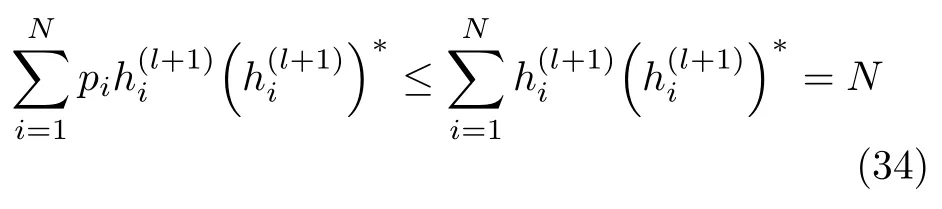
结合式(32)和上文推导矩阵R(l)的结果，则容易得到式(2 7)的表达式。定义两个变量α=εN(N+λ1−1)+(1−ε)(τ/Ts)N(N+1)和β=εN·(N+λ1−1)+(1−ε)(τ/Ts)N+(1−ε)N2。由于R(l)和T(l+1)是半正定矩阵，故可得到下述关系式R(l)≺αIN和T(l+1)≺βIN。因此，根据主分量最小化原理，利用α和β分别替换矩阵R(l)和T(l+1)的迹仍可保证算法迭代过程中的目标函数是单调下降的。

通过推导矩阵R(l)和T(l+1)的迹，有效避免了计算上述两个矩阵引起的矩阵乘法运算。因此，本文所提算法的计算复杂度仅源于式(17)和式(23)第1项的矩阵和向量乘法运算。因此，算法的计算复杂度为O(N2)。

3.5 算法加速

在主分量最小化函数方法中，由于使用了主分量函数近似等价目标函数，目标函数收敛速度将会大幅度下降。文献[28]提出了平方迭代方法，其通过联合利用最速下降法和两点步长梯度方法可以实现对EM (Expectation-Maximization)算法加速。EM算法基本思路是先根据第l次迭代结果求取联合条件概率期望的极大似然函数，然后根据上述函数更新第l+1次的优化解。另外，主分量最小化方法首先根据第l次迭代结果求目标函数的主分量最大化函数，然后基于此求第l+1次迭代解析表达式[28]。因此，主分量最大化算法和EM算法工作流程基本是一致的。受此启发，本文将平方迭代方法应用于本文基于主分量最小化的联合波形和滤波器设计方法。除此之外，平方迭代方法仅要求EM算法的更新策略，即波形和滤波器迭代更新表达式，故可直接在算法中进行应用。

分别利用α和β替换式(16)和式(22)中的迹表达式，定义如下两个映射函数：

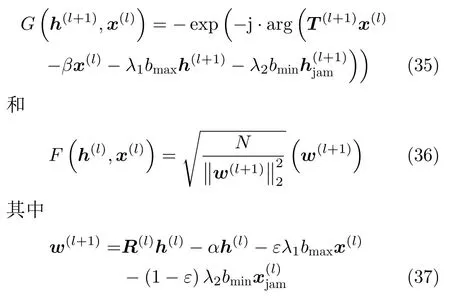
利用平方迭代加速方法对算法进行加速，抗间歇采样转发干扰联合优化设计算法如表1所示。在本文所提方法中，分别对波形和滤波器迭代过程中应用平方迭代加速方法。其中，滤波器的更新加速对应表1的步骤4—步骤12，而波形的更新加速对应表1的步骤14—步骤22。其中，平方迭代加速方法的基本原理已在文献[22,29]中详细介绍，此处不再赘述。由于在加速过程并未引入额外的矩阵乘法等运算，故加速算法的计算复杂度仍为O(N2)。

表1 快速抗间歇采样转发干扰波形和滤波器联合设计算法Tab.1 Fast algorithm for joint waveform and filter design against interrupted sampling repeater jamming

4 仿真

为了验证本文所提算法的有效性，本节开展7个仿真实验。首先对联合设计模型中关键参数进行仿真分析。通过对比传统方法，分析了本文所提方法运行速度的性能。同时，为了评估联合设计的抗干扰性能，将本文所提方法与传统抗间歇采样转发干扰进行了对比分析。最后，对本文所提方法的干扰参数敏感性进行了分析。所有的仿真实验均在同一个硬件和软件平台开展(PC with 4.20 GHz Intel Core i7-7700K CPU and 64GB RAM using Windows 7)。

4.1 算法性能分析

仿真1：假设波形和非匹配滤波器长度为512，波形非匹配滤波输出归一化峰值增益损耗为–1 dB，干扰信号非匹配滤波输出归一化峰值为–30 dB。算法截止运行阈值ζ=1e−7。间歇采样信号占空比0.25，间歇采样周期重复Ts=T/2。首先分析帕累托权值对算法性能的影响，帕累托权值ε=[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]。不同帕累托权值条件下的波形和非匹配滤波器初始序列分别为同一随机相位编码序列。

图1为波形非匹配脉冲压缩积分旁瓣比和峰值损耗，以及干扰信号非匹配滤波输出积分能量和峰值随着帕累托权值的变化曲线图。如图1(a)和图1(c)所示，随着帕累托权值的增加，积分旁瓣比呈现下降趋势，而峰值损耗值逐渐增加。由目标函数的定义可知，当帕累托权值增加时，目标函数中提高脉冲压缩性能的权重增加。因此，在优化过程中能够使得目标函数f1(x,h)的数值更小，即积分旁瓣和峰值损耗目标函数的数值将会逐渐减小。其中，脉压峰值目标函数减小会使得设计波形和滤波器的脉压峰值和预期设定值之间的误差值逐渐降低，所以设计波形和滤波器的脉压峰值将逐渐靠近预期设定值，进而符合逐渐上升趋势。此外，权值为0.3和0.8时积分旁瓣比水平值分别要小于权值为0.4和0.9时对应的数值，这可能与算法的迭代次数相关，即权值为0.3和0.8时迭代次数少于权值为0.4和0.9时对应的迭代次数，进而导致其积分旁瓣值偏大。同时，图1(b)和图1(d)中干扰信号的积分能量比、干扰峰值随着帕累托权值的增加，干扰信号非匹配滤波输出峰值干扰增加。其原因是帕累托权值增加使得抑制干扰的代价函数权重降低，进而导致干扰信号非匹配滤波输出峰值增加。

由图1仿真分析可知，随着帕累托权值的增加，雷达波形脉冲压缩性能与抗间歇采样转发干扰的性能变化趋势是相反的。也就是说，很难同时获得高脉冲压缩性能和抗间歇采样转发干扰性能。实际上，参数的选择可以根据场景中间歇采样转发干扰的功率强度决定。在干扰强度较大的情况下，可以设置较小的权值以使得联合设计的波形和滤波器能够获得更优的抗干扰性能。而当干扰强度较小时，则设置较大的权值，使得联合设计的波形和滤波器能够在维持更好的脉冲压缩性能的同时获得抗间歇采样转发干扰性能。为了平衡设计波形的抗干扰性能和脉冲压缩性能，本文将帕累托权值设置为0.5。

图2为帕累托值为0.5时本文所提方法设计的波形实部和幅度图，其满足恒模约束。图3为设计的波形及其对应的干扰信号经过非匹配滤波输出后的结果图。图3(a)为波形非匹配滤波脉冲压缩结果图，其归一化峰值增益损耗为–1.03 dB，积分旁瓣比为–12.46 dB。图3(b)为干扰信号非匹配滤波输出结果图，其归一化峰值干扰为–28.43 dB，积分能量比为–14.22 dB。因此，其达到了同时抑制波形脉冲压缩积分旁瓣和间歇采样转发干扰的目的。

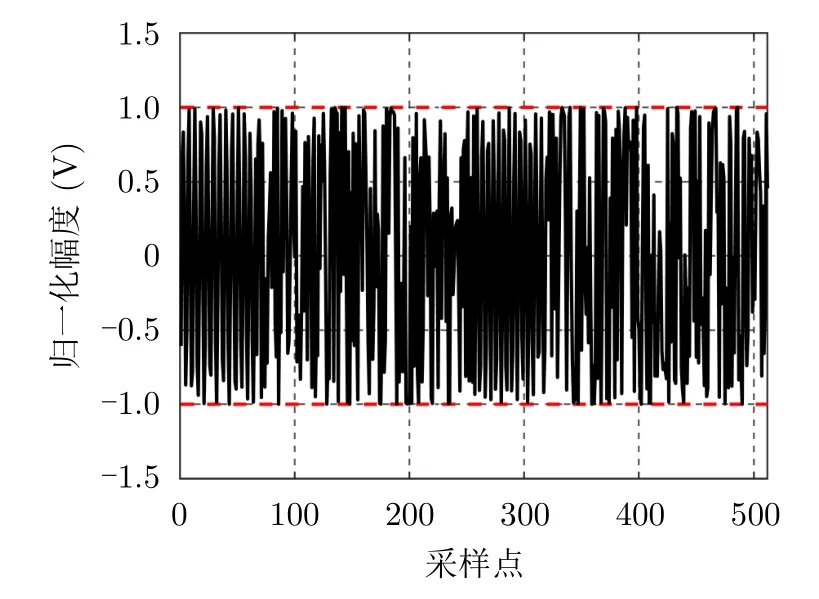
图2 波形实部幅度图Fig.2 The amplitude of the real part of waveform

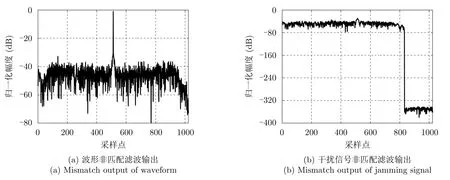
图3 波形和干扰信号非匹配滤波输出(N=512)Fig.3 Mismatch output of the waveform and jamming signal (N=512)

仿真2：分析峰值增益损耗对波形非匹配滤波输出积分旁瓣性能和干扰信号积分能量性能的影响。峰值增益损耗[–0.8,–1.0,–1.3,–1.6,–2.0]，其余参数与上述一致。由于波形中间歇采样部分的信号段被抑制，所以波形的非匹配滤波输出存在峰值增益损耗。图4为雷达波形非匹配滤波输出积分旁瓣比和干扰信号积分能量随着峰值增益损耗变化曲线，可以发现，随着峰值增益损耗绝对值的减小，积分旁瓣比和干扰信号积分能量逐渐增加。因此，为了有效抑制间歇采样转发干扰，并且提高波形脉冲压缩积分旁瓣水平，峰值增益损耗不应太小。

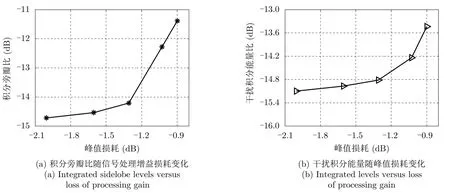
图4 积分旁瓣比和积分能量比随峰值增益损耗变化Fig.4 Integrated sidelobe levels and integrated levels versus loss of processing gain

仿真3：对比分析本文所提算法和传统方法的运行时间。假设波形和非匹配滤波器长度为128，干扰信号非匹配滤波输出归一化峰值为–30 dB。间歇采样信号占空比0.25，间歇采样周期重复Ts=Tp/4。算法截止运行阈值ζ=1e−7，帕累托权值ε=0.5。首先利用文献[17]所提出的方法设计一组波形和非匹配滤波器，其性能如表2所示。为了公平比较，本文所提算法和文献[18]方法的波形非匹配滤波输出归一化峰值增益损耗为LPG=–1.7 dB，权值λ1=λ2=256，且其余参数设置与文献[17]算法一致。除此之外，所有对比方法的波形和非匹配滤波器初始序列均一致。图5为两种方法目标函数随运行时间变化曲线，可以发现本文所提方法速度远快于本文的对比方法。

图5 运行时间对比图Fig.5 Comparison of running time

表2 算法性能对比Tab.2 Performance comparison of tested algorithms

表2为两种算法设计波形和非匹配滤波器的性能对比，可以发现在相同峰值增益损耗情况下，本文所提方法的波形非匹配滤波脉冲压缩积分旁瓣比和干扰信号非匹配滤波输出积分能量值均低于文献[17]方法。但是本文设计方法干扰信号非匹配滤波输出峰值大于文献[17]方法，这是因为本文设计方法的干扰峰值是通过最小化目标函数控制的，其值只能无限趋向于零，而难以精确控制为零。并且，可以发现在脉压性能和抗干扰性能接近的情况下，本文所提算法的速度显著提升。

仿真4：为了评估本文分析提出的理论计算复杂度，开展了一组仿真。假设设计波形长度为[32,64,128,256,512,1024]，对每个长度波形开展10组仿真，并记录每次运行时间。其中算法的截止条件仍为ζ=1e−7。图6为不同波形长度下的平均运行时间图。不同信号长度波形设计的算法平均运行时间分别为2.23,10.11,43.57,125.91,506.61和2027.12 s。可以发现，信号长度每增加一倍，算法运行时间增加3倍。这说明，随着信号长度增加，算法的运行时间按照平方次数增加，进而说明本文所提方法计算复杂度为O(N2)。

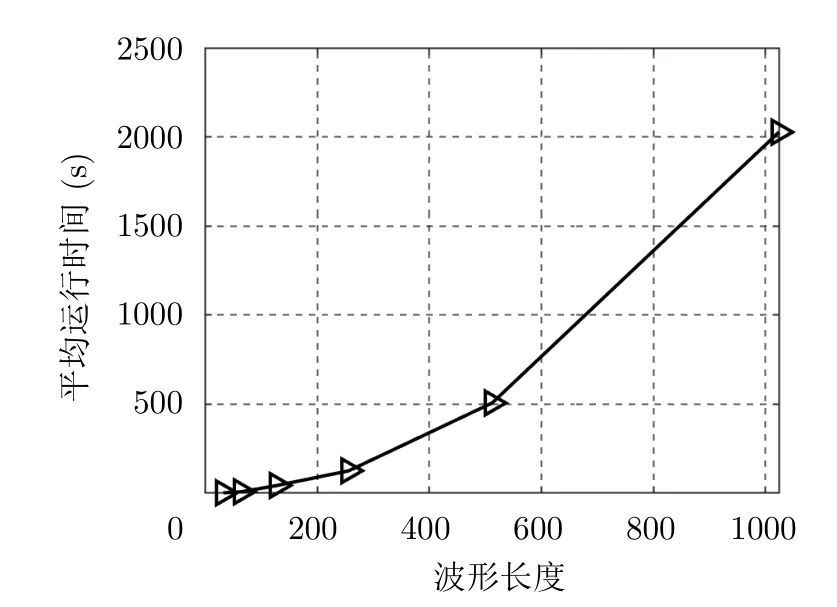
图6 不同波形长度下的运行时间图Fig.6 Running time versus different code length

4.2 抗干扰性能评估

仿真5：评估本文所提方法抗干扰性能。仿真场景参数如表3所示。以SPL文献中相关结果作为参考，设置本文方法相关参数，其中峰值增益损耗为–1.6 dB。图7为本文设计的波形和干扰信号非匹配滤波输出结果。表4为两种方法设计的仿真结果性能对比表。可以看出，设计的波形非匹配滤波脉冲压缩峰值增益损耗一样，而本文所提方法的积分旁瓣比和积分能量比性能均优于文献[17]方法。

表3 仿真参数Tab.3 Simulation parameters

表4 两组波形和非匹配滤波器性能对比Tab.4 The mismatch output performance of designed waveform via tested algorithms

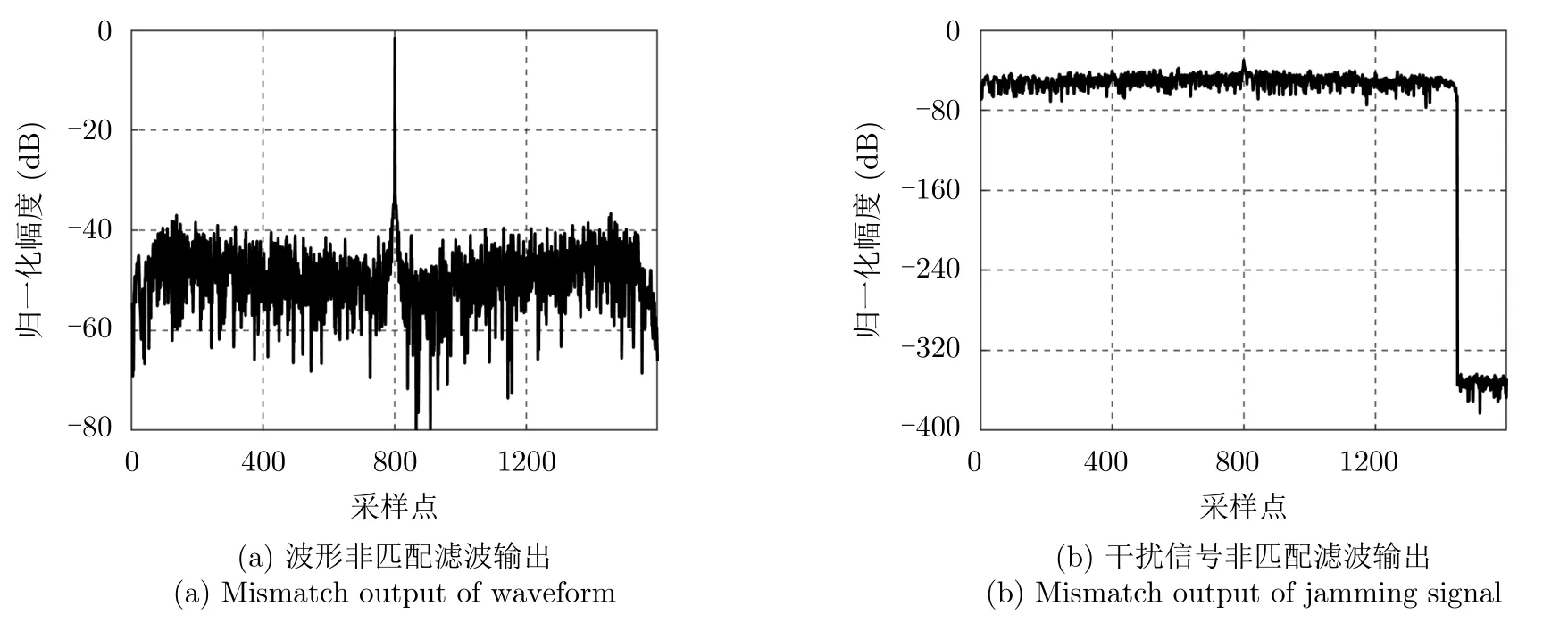
图7 波形和干扰信号非匹配滤波输出(N=800)Fig.7 Mismatch output of waveform and jamming signal (N=800)

仿真6：为评估本文的抗干扰性能，将本文方法和文献[10]、文献[13]、文献[17]得到的抗干扰结果进行了对比分析。仿真参数如表3所示，干扰机的转发模式为重复转发干扰，转发次数为2次。信噪比为0 dB，信干比为–20 dB。图8为抗干扰得到的仿真结果，其中所有结果均通过发射信号能量进行归一化。图8(a)—图8(d)分别为文献[13]、文献[10]、文献[17]和所提方法得到的仿真结果。表5为抗干扰仿真结果性能对比。可以发现，本文和文献[17]提出的方法信号处理增益存在损耗，这是由非匹配滤波器引起的。相较于文献[13]和文献[17]提出的方法，本文所提出的方法的干扰峰值是最低的，并且干扰导致的假目标的数量也是最少的。但是，相较于文献[10]提出的方法，本文的干扰峰值显著偏高，并且其旁瓣的值也显著低于其他3类对比方法。这是因为在干扰和目标距离可分辨情况下，通过干扰识别出目标所在距离单元后，文献[10]提出的方法可在时频域实现对干扰能量的完全抑制。

表5 抗干扰性能对比Tab.5 Performance comparison of jamming suppression

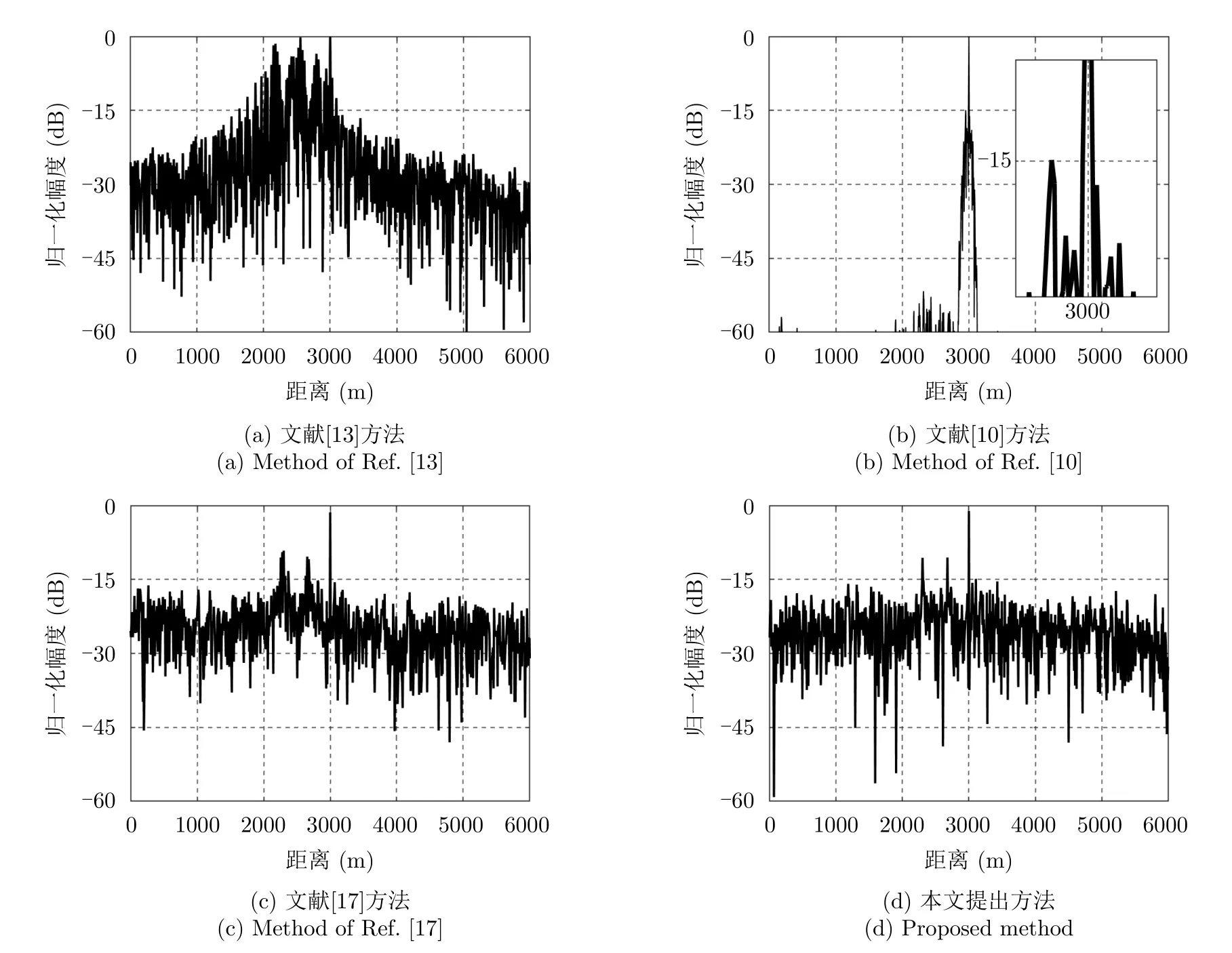
图8 抗间歇采样转发干扰评估Fig.8 Evaluation of interrupted sampling repeater jamming suppression

其次，进一步分析干扰机位置变化对本文方法和文献[10]抗干扰性能，以验证本文所提方法的优越性。假设干扰机的位置从2000 m到3000 m逐渐增加，增加的间距为20 m。其余的仿真参数与表2一致。同时每个位置开展100次蒙特卡罗仿真，并记录其干扰峰值。图9为本文方法和文献[10]抗干扰性能随着干扰机位置变化的结果图。可以发现，当干扰机和目标位置不可分离时，文献[10]所提方法的抗干扰性能将显著下降。这是因为，当干扰目标和实际目标处于临近距离单元时，时频域滤波将难以有效实现对干扰信号的抑制。这说明，当干扰目标和实际目标可分离时，文献[10]提出的方法抗干扰性能优于本文所提方法。但是，本文所提方法仅需要估计干扰机的占空比和周期参数，设计发射波形和非匹配滤波器后即可实现干扰信号非匹配输出峰值和积分能量抑制。相较于文献[10]所提方法，本文所提方法在信号处理过程中仅需要利用非匹滤波进行脉压即可得到抗干扰一维距离像，而无需根据脉压后的时频特性差异对干扰和目标回波进行辨识与抑制，故本文所提方法抗干扰性能不受干扰目标和真实目标之间的相对距离影响。当目标和干扰目标不可分离时，本文提出方法的性能显著优于文献[10]提出的方法。因此，相较于文献[10]提出的方法，本文所提出的方法抗干扰性能不受干扰目标和真实目标相对距离影响，普适性更强。

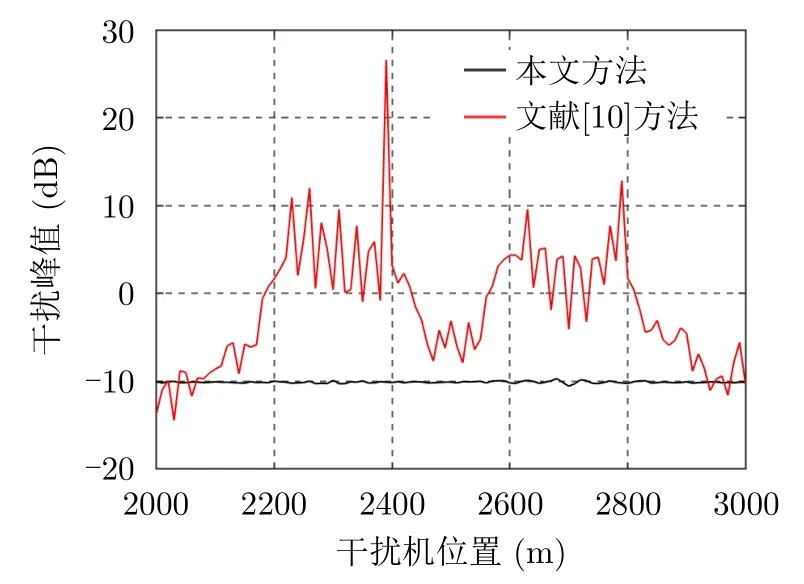
图9 干扰机位置对抗干扰性能的影响Fig.9 Jamming suppression performance versus location of jammer

4.3 干扰参数敏感性分析

仿真7：为了评估干扰采样占空比和重复周期两个关键参数对抗干扰性能的影响，开展了一组参数敏感性分析实验。间歇采样重复周期和占空比的估计误差变化范围为±10%，误差间隔1%取一个周期和占空比数值。在每个误差数值处分别开展100次蒙特卡罗仿真实验，并记录脉冲压缩后的归一化干扰峰值。本仿真中，设置信干比为–15 dB，信噪比为0 dB，干扰机位置为(0,2200,0) m，其余仿真参数如表2所示。由图9可知，由于干扰机的位置为导致干扰目标和真实目标之间不可分离，因此文献[10]所提方法此时无法有效抑制干扰。此外，我们与文献[13]所示方法进行了进一步对比，且忽略其干扰信号重构过程中的干扰信号幅度误差。需要说明的是，由于假设其干扰重构幅度是无误差的，因此在间歇采样重复周期和占空比精确也无误差时，其抗干扰性能会比图8(a)对应的结果更好。

图10为干扰峰值随着重复周期和占空比的估计误差变化图。由图10(a)可知，文献[13]所提的方法对间歇采样转发重复周期十分敏感。这是因为，间歇采样转发重复周期的误差均会导致重构干扰信号与实际干扰信号之间存在显著差异，进而导致抗干扰性能的下降。本文所提的抗干扰性能受间歇采样转发重复周期的影响较大，当相对误差变化大于1.5%时，干扰输出峰值大于–5 dB。由图10(b)可知，当相对误差为负数，即实际干扰占空比小于联合设计过程中设置的占空比，本文所提方法抗干扰性能几乎不受影响，而文献[13]所提方法的抗干扰性能则会逐渐降低。当实际干扰占空比大于参数估计得到占空比时，本文所提方法抗干扰性能恶化速度快于文献[13]所提的方法。当相对误差大于5%时，本文所提方法的干扰峰值大于–5 dB。因此，相较于文献[13]所提的方法，本文所提方法与其间歇采样周期敏感性基本一致。而两种方法对占空比的敏感性则视估计误差而定。如果估计的占空比值大于实际干扰机占空比，即估计误差为负数时，本文所提方法对占空比的敏感性低于文献[13]所提的方法；反之，则本文所提方法对占空比参数更敏感。

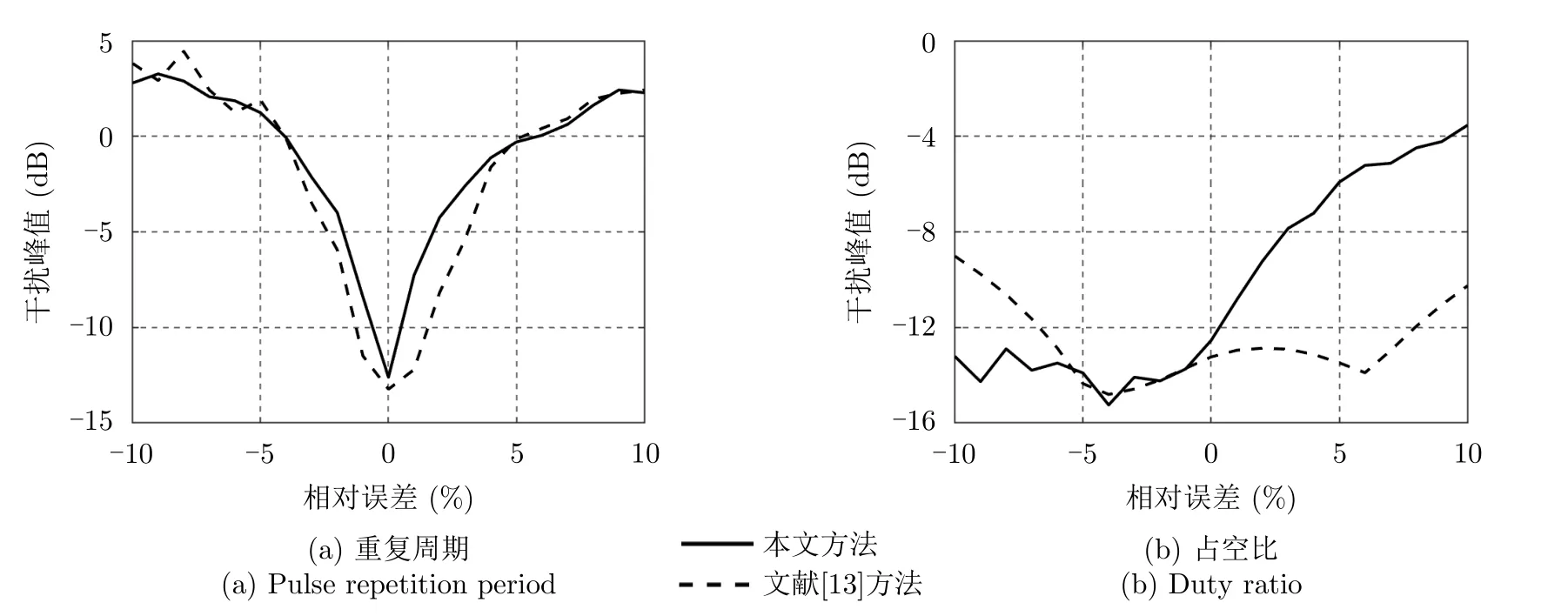
图10 干扰峰值随着重复周期和占空比的估计误差变化图Fig.10 Jamming peak versus the relative error of pulse repetition period and duty ratio

5 结论

本文研究了抗间歇采样转发干扰的快速波形和滤波器联合设计算法。相较于传统方法，本文设计的波形和滤波器可以实现抑制间歇采样转发干扰。本文所提出的设计算法计算复杂度为O(N2)，显著优于传统方法。仿真结果验证了本文所提加速算法的有效性，其算法运行速度显著优于传统方法。此外，相较于传统的时频信号处理方法，本文所提方法能够在干扰目标和真实目标距离不可分离时仍达到抑制干扰的目的。本文所提算法是在间歇采样信号周期和占空比先验知识抑制情况下开展的波形和滤波器联合设计，并且本文所提方法对干扰采样周期十分敏感。因此，干扰信号周期和占空比参数的精确估计是下一步研究的重点。