优化初中数学教学 培养学生核心素养

李继江

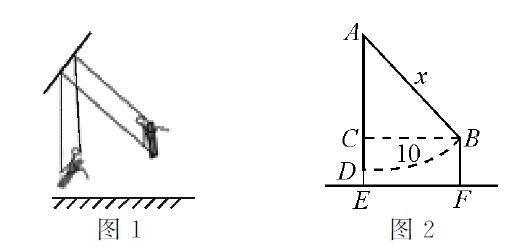
摘要：本文中主要从“让数学问题走进生活，加强数学问题规律研究，引导数学问题模型化，将数学问题实际操作化”这四个方面优化教学积极引导学生在探究过程中“再发现”，培养学生的探究意识、推理意识，以及数学应用意识，提升实践能力和数学核心素养.

关键词：核心素养；初中数学；优化策略；研究；视角

数学核心素养并不是确切指某种理论知识，也不是掌握某种数学方法，而是学生在成长过程中需要具备的个人素质.在数学教学中如何培养学生的核心素养呢？这就要求教师在核心素养视角下加强数学问题研究，从根本上提升学生的综合能力，真正发展学生运用数学知识与方法发现、提出、分析和解决问题的能力，从而在学习过程中形成数学学科的核心素养.下面就如何优化教学策略以提高学生核心素养谈谈自己的做法.

1 让数学问题走进生活，激发学生学习兴趣

苏科版教材中“数学活动”有这样的一个示例：算“24”是一种常见的扑克牌游戏.我们约定一副扑克牌中的黑色数字为正数，红色数字为负数，J表示11，Q表示12，K表示13，A为1，2张JOKER均为0.将一副扑克牌平均分给每个人，每人每次出4张牌.4张牌的点数都是1～13中的某个数.

游戏中，小强抽到以下4张牌：方片2，黑桃5，梅花J，红桃Q.请你用这四张牌表示的数写出运算结果为24的算式（写出1个）．

有理数的混合运算就自然而然地融入到了数学游戏之中，在教学中，学生的学习兴趣也就自然增加了.这样的情境下，打扑克游戏已经不是纯粹地玩，而是一种益智活动.持续开展数学游戏活动，学生会在玩中发现更多更奇妙的游戏规则，也会发现或者提出更多有意义的数学问题.

再如一些教材中出现的“七巧板”活动.七巧板起源于我国先秦时期，古算书《周髀算经》中有关于正方形的分割术．据清代陆以湉《冷庐杂识》记载，七巧板是由宋代黄伯思设计的“宴几”图演变而来的，原为文人的一种室内游戏，后在民间逐步演变为拼图版玩具．教材借助折叠七巧板活动，不但引导学生通过动手实践，认识七巧板的多种几何形状，更加激发了学生的学习或研究兴趣，从简单的图形，到形象逼真的图象，再到富有内涵的几何标志，等等，不断地激发着数学爱好者层层深入，获得更多更丰富的内容.

2016年第七届世界历史文化名城博览会在南京举办．以“多元，开放，创造”为定位，其会徽是运用“七巧板”元素组合而成的“一件云锦嫁衣”图案，由国际著名平面设计大师、荷兰艾因霍芬设计学院院长托马斯设计完成．

随着数学知识的深入学习，对图形的简单认识逐渐过渡到数学计算.例如，某市人民正在积极开展创建“全国文明城市”的运动，聪明的学生用七巧板拼成一副孔子像，并通过相关数据计算孔子像的高度．

让数学问题走进生活，可以逐步培养学生从数学角度观察现实世界的意识和习惯，从而不断地激发学生的好奇心和探究兴趣.

2 加强数学问题规律研究，调动学生的探究意识苏科版八年级上册数学教材中“数学活动——探寻勾股数”中，从简单的图形入手，探寻勾股数的存在规律，意在调动学生的探究意识.在了解基本勾股数之后，继续深入探寻“勾股数”：直角三角形三边长是整数时我们称之为“勾股数”，那么勾股数有多少？勾股数有规律吗？在引导学生探究的过程中，明确勾股数的基本特点，即“两个数的平方和（或差）等于第三个数的平方”，从而确定了勾股数满足的形式：（）2+（）2＝（）2；或（）2-（）2＝（）2.我们已经知道（x+y）2-（x-y）2＝4xy，如果等式右边的4xy也能转化为某正整数平方的形式，就能满足勾股数的形式了.通过再次探究，假设x＝m2，y＝n2，m，n为任意正整数且m＞n，则恰好能实现这一要求，即有（m2-n2）2+（2mn）2＝（m2+n2）2，从而得出了勾股数满足的条件.

结合本例我们发现，如果深入探究生活中的小问题或者数学情境，发现其中涵含的数学规律，学生讲道理、有条理的思维品质也会逐步养成.

在学习了“用字母表示数”这一节后，教材补充了“阅读”内容，这部分内容表述如下：人们通过长期观察发现，如果早晨天空中有棉絮状的高积云，那么午后常有雷雨降临，于是有了“朝有破絮云，午后雷雨临”的谚语.紧跟着提出了数学问题：三角形有3个顶点，如果在它的内部再画n个点，并以这（n+3）个点为顶点画三角形，那么最多可以剪得多少个这样的三角形？如何解决此类的问题？引导学生学会探究归纳：为了解决这个问题，我们可以从n＝1，n＝2，n＝3等具体、简单的情形入手，探索最多可以剪得的三角形个数的变化规律．

此类问题的解决，在一步步引导学生观察、比较中深入发展下去，并借助计算、推理发现其存在的规律，不知不觉中让学生构建了数学逻辑体系，并培养了良好的科学态度与理性精神.

3 引导数学问题模型化，培养学生模型观念

将数学问题简约化，其实就是将模型观念融入数学问题之中，借助对数学模型的运用解决实际问题，并能有清晰的认识.

教材在“一元二次方程”后的“数学活动”中提出这样的问题：在一块长33 m，宽24 m的矩形绿地内，要围出一个花圃，使花圃的面积是矩形面积的一半，你能给出设计方案吗？再进一步引发学生思考：花圃可以有多种设计方案，例如，在绿地中间可以开辟一个矩形的花圃，使四周的绿地等宽，绿地的面积与花圃的面积相等，你能计算出绿地的宽吗？通过对数学问题情境的分析，可以建立一元二次方程模型解答，从而将复杂问题简单化.基本问题得到解决后，再引导学生进一步探索：请你再设计两种不同的方案，并交流你设计的方案有哪些特点.通过提出的问题，充分考查学生的思维开放性、应用数学的意识及探索能力，不但涉及学生的画图设计能力，还有动手操作的能力.

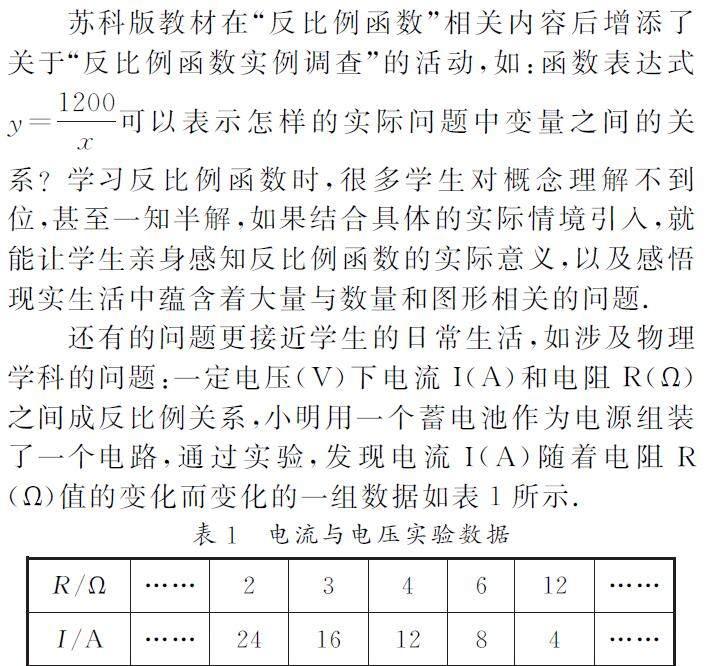
当然这类问题在古代数学文化中也屡见不鲜.明朝数学家程大位在数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千“问题：平地秋千未起，踏板一尺离地．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索有几？如果我们仅仅是针对著作中表述的问题去理解分析，可能对学生来说，难上加难，然而，将难懂的古文言文字转化为现代汉语来理解问题则简单易懂.译文：如图1，有一架秋千，当它静止时，踏板离地1尺，将它往前推送10尺（水平距离）时，秋千的踏板就和人一样高，这个人的身高为5尺，秋千的绳索始终拉得很直，试问绳索有多长？（注古代5尺为1步）结合图形，文字内容更加生动形象，如图2所示，将描述性问题转化为数学模型来解答，真正让学生感受到数学语言的魅力.

数学模型如下：如图2，秋千绳索AD静止的时候，踏板离地高一尺（DE＝1尺），将它往前推进两步（CB＝10尺），此时踏板升高离地五尺（BF＝5尺），已知AE⊥EF于点E，BF⊥EF于点F，BC⊥AE于点C，AD＝AB．请解答下列问题：（1）四边形ECBF是哪种特殊的四边形？请证明你的结论；（2）求AB的长．

4 将数学问题实际操作化，增强学生的应用意识

数学中的有些问题，我们只有通过具体操作后，才能更好地理解把握，才能更好地进行应用.因此很多问题需要我们在实践中落实，让问题实践化，更容易调动学生的积极性，增强他们的应用意识.

苏科版教材在“反比例函数”相关内容后增添了关于“反比例函数实例调查”的活动，如：函数表达式y=1200x可以表示怎样的实际问题中变量之间的关系？学习反比例函数时，很多学生对概念理解不到位，甚至一知半解，如果结合具体的实际情境引入，就能让学生亲身感知反比例函数的实际意义，以及感悟现实生活中蕴含着大量与数量和图形相关的问题.

还有的问题更接近学生的日常生活，如涉及物理学科的问题：一定电压（V）下电流I（A）和电阻R（Ω）之间成反比例关系，小明用一个蓄电池作为电源组装了一个电路，通过实验，发现电流I（A）随着电阻R（Ω）值的变化而变化的一组数据如表1所示．

根据上述表述进一步提出问题：求这个蓄电池的电压值；请在坐标系中，通过描点画出电流I和电阻R之间的关系图象，并直接写出I和R之间的函数关系式；若该电路的最小电阻值为1.5 Ω，请求出该电路能通过的最大电流．

诸如上述教材中都可能涉及到的相关材料，都是在引导学生关注生活中与数学相关的信息，激发学生的社会参与意识，并主动参与到数学活动中，感受数学的实际应用价值，体会数学的奥妙.

总之，教师只要充分利用教材典型材料，将其融入生活中，及时归纳总结，并引导学生不断用数学语言进行问题交流，了解并领会数学的价值，欣赏数学的美，建立学好数学的信心，真正形成数学思想，形成质疑问难、勇于探索的科学精神.