利用卫星跟踪卫星观测数据确定时变重力场球谐解的发展趋势
周 浩,罗志才,周泽兵,杨 帆,郭 向,李耀宗,郑李均,郑舒允
1 华中科技大学 精密重力测量国家重大科技基础设施,武汉 430074
2 华中科技大学物理学院 地球物理研究所 基本物理量测量教育部重点实验室,武汉 430074
0 引 言
时变重力场综合反映了地球内部及表层物质的迁移特性,可为全球或区域水资源管理、自然灾害监测与防治等应用提供重要的基础信息,是发展当前大地测量学、地球物理学、海洋学、冰川学等学科急需的基础观测信息之一(Tapley et al., 2004; 陈俊勇等, 2005; 许厚泽等, 2012; 宁津生等, 2013).
自21世纪以来,CHAMP、GRACE、GOCE和GRACE Follow-On等重力卫星相继成功实施,为实现全球重力场观测提供了重要保障,并为时变重力信号的获取提供了全新途径. CHAMP卫星采用高低卫星跟踪卫星模式,可获取地球重力场的长波信息;GOCE卫星采用重力梯度测量模式,对地球重力场的中短波信息较为敏感,但受限于星载重力梯度仪的测量带宽限制,对地球重力场长波信息恢复得较差;GRACE和GRACE Follow-On卫星采用低低卫星跟踪卫星模式,对地球重力场的中长波信息最为敏感,为获取高精度高分辨率的时变信息提供了可能(Reigber et al., 2002; Drinkwater et al., 2003; Tapley et al., 2004; Pail et al., 2011;Kornfeld et al., 2019). 自GRACE成功发射以来,时变重力场的应用范围得到了极大推广,为全球变化与地表过程、人类活动及其生态效应、水循环与生态水文过程、干旱环境系统与全球环境变化等地球科学研究提供了大量的观测信息,为人类了解地球内部构造及浅层物质迁移开启了新纪元.
高精度高分辨率的时变重力场模型是开展相关科学研究的重要保障,如何利用卫星重力观测信息获取高精度高分辨率的时变重力场模型,是当前大地测量领域亟待解决的关键科学问题之一. 随着重力卫星观测数据的累积、对观测数据的认知更为深入以及观测方法的逐步更新,近年来相关领域关于时变重力场精细建模的研究成果不断涌现. 本文将综述基于卫星跟踪卫星观测数据实现时变重力场球谐解精细建模的主要进展,并展望下一代重力卫星确定时变重力场模型面临的新挑战.
1 低低卫星跟踪卫星确定时变重力场
1.1 低低卫星跟踪卫星观测的基本原理
所谓低低卫星跟踪卫星观测技术,即通过精确测量距离数百千米的两颗低轨卫星之间的距离及其变化量,从而获取高精度地球重力场静态及时变观测信息(Wolff, 1969). GRACE和GRACE Follow-On卫星均采用低低卫星跟踪卫星观测技术,也是目前获取地球中长波静态及时变信息最为有效的观测手段(Tapley et al., 2004; Kornfeld et al., 2019).
若将地球视为均质刚性球体,则两颗卫星在万有引力作用下呈匀速圆周运动;由于地球是一个物质分布不均匀的弹性体,两颗卫星在空间不同位置受力各不相同,使得卫星之间的相对距离时刻发生变化. 如图1所示,当首部卫星接近高山时,卫星受力更大,双星距离逐步增加;当首部卫星飞离高山时受到拖拽力,而尾部卫星到达高山附近受到牵引力,双星距离逐步减小;双星均飞离高山时,双星距离逐步恢复. 总体而言,当卫星飞过正质量异常时,双星距离经历先增加再减小的过程. 通过精密测量两颗卫星之间的距离,可实现地球质量异常分布特征的精细探测,即地球重力场的精确测量.通过多期重复观测,可精确测定地球重力场随时间的变化特征,即时变重力场的精确测量.

图1 重力卫星经过质量块时速度(红色箭头)与受力(蓝色箭头)的变化示意图Fig. 1 Variation of velocity (red arrow) and force (blue arrow) of gravity satellites when they pass through a mass block
由低低卫星跟踪卫星观测的基本原理可知,实现时变重力场精确测量的关键是星间距离的精确测量. GRACE卫星主要采用微波测距系统KBR(Kband ranging system),在距离220 km双星之间的测量精度可达到μm级(Tapley et al., 2004).GRACE Follow-On卫星除了搭载KBR,还首次搭载了激光测距系统LRI(laser ranging interferometer),其测量精度可达到nm级(Abich et al.,2019). 同时,为了有效剔除非保守力对卫星的影响,卫星搭载了高精度的静电悬浮加速度计.GRACE和GRACE Follow-On卫星搭载加速度计的灵敏轴方向的测量精度水平为10-10m/s2,而华中科技大学为天琴一号卫星设计的加速度计精度水平达到10-12m/s2,且在国际上首次实现在轨评估精度达到10-11m/s2,为我国重力卫星建设提供了重要技术保障(Luo et al., 2020).
1.2 时变重力场球谐解的建模方法
利用重力卫星高精度载荷可获取海量的观测数据,为时变重力场观测提供了重要数据保障. 如何利用海量观测数据实现时变重力场精细建模,是大地测量学领域的热点和难点问题. 自低低卫星跟踪卫星概念提出以来,国内外学者围绕时变重力场球谐解建模方法开展了一系列研究,主要的建模方法包括解析法、半解析法和数值法. 其中,解析法和半解析法主要用于重力卫星一体化任务设计,而数值法能够充分利用观测信息的特征,在实测数据解算中得到了广泛应用. 数值法本质上是关于求解重力场位系数的最小二乘估计方法,常用的数值法有动力法(Reigber, 1989)、短弧法(Mayer-Gürr, 2006)、天体力学法(Beutler et al., 2010)、加速度法(Ditmar et al., 2004)、能量法(Bjerhammar, 1967)等. 其中,天体力学法与动力学法极为相似,仅仅只是对加速度计数据处理存在一些差异,因此通常不作为独立方法进行评价. Baur等(2014)为了精细比对不同方法的差异,集合多家重力场建模中心反演结果进行了比对研究(如图2). 结果表明,由于能量法仅采用单一标量参与解算,其解算精度比其他方法更低;其余方法反演重力场的精度水平几乎一致,证实各种方法理论上均能够实现重力场的精细建模.
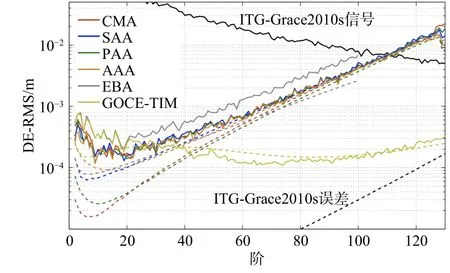
图2 不同重力场反演方法的结果比对. CMA:天体力学法;SAA:短弧法;PAA:点加速度法;AAA:平均加速度法;EBA:能量守恒法;GOCE-TIM:GOCE-时域法(修改自Baur et al., 2014)Fig. 2 Degree errors RMS w.r.t. ITG-Grace2010s of spherical harmonic coefficients (log 10 representation). Results based on GOCE kinematic orbit analysis using the celestial mechanics approach (CMA), short arc approach(SAA), point-wise acceleration approach (PAA), averaged acceleration approach (AAA), and enerage balance approach (EBA) (modified from Baur et al.,2014)
在国际上,GRACE重力卫星官方数据处理机构美国得克萨斯大学空间科学中心CSR(Center for Space Research, Bettadpur, 2018)、美国宇航局喷气推进实验室JPL(Jet Propulsion Laboratory,Yuan, 2018)和德国地学研究中心GFZ(Geo-ForschungsZentrum Potsdam, Dahle et al., 2018)均采用动力法建立时变重力场模型. 除此之外,格拉茨技术大学大地测量研究所ITSG(Institute of Geodesy, Graz University of Technology, Kvas et al.,2019)和法国空间研究中心空间大地测量研究所GRGS(Groupe de Recherche de Geodesie Spatiale,Lemoine et al., 2019)也主要采用了动力法,而伯尔尼大学天文研究所AIUB(Astronomical Institute,University of Bern, Lasser et al., 2020b)主要采用了天体力学法,波恩大学理论大地测量研究所ITG(Institute of Theoretical Geodesy, Mayer-Guerr et al., 2010)主要采用了短弧法,代尔夫特地球观测与空间系统研究所DEOS(Delft Institute of Earth Observation and Space System, Liu et al., 2010)主要采用了加速度法. 基于上述研究方法,各个机构先后发布了GRACE时变重力场模型序列.
自GRACE卫星成功发射以来,我国大量学者对重力卫星建模方法开展了一系列的跟踪研究,为推进我国重力卫星事业提供了重要的技术支撑. 徐天河(2004)、王正涛(2005)、周旭华(2005)、肖云(2006)、张兴福(2007)、郑伟(2007)、邹贤才(2007)、王庆宾(2009)、游为(2011)等先后利用模拟观测数据开展了大量开创性研究,为卫星重力场建模理论与方法的构建提供了重要基础. 在此基础上,冉将军(2013)、苏勇(2015)、王长青(2015)、周浩(2015)、陈秋杰(2017)、郭南男(2017)、郭向(2017)、杨帆(2017)、梁磊(2019)等先后利用实测数据研究时变重力场建模的理论与方法,先后建立了多个时变重力场模型,为拓展时变重力场应用及推进我国自主重力卫星研制积累了宝贵经验.
从卫星的观测原理和时变重力场模型的建模方法可知,时变重力场球谐解建模主要与观测数据精度、摄动力模型精度和建模方法等因素密切相关.因此,下文将主要从上述三个方面出发,论述现阶段时变重力场球谐解建模的主要研究进展.
1.3 关键载荷观测数据的精细处理
重力卫星数据采用分级管理方式,分为L0、L1A、L1B、L2和L3数据. L0为原始观测数据;L1A为对L0数据进行非破坏性处理的结果,主要包括转换科学单位、添加时间标记和质量控制标示等过程;L1B对L1A数据进行了时标改正、滤波、重采样等一系列不可逆的处理,是重力场反演的输入数据;L2和L3是科学数据产品,包括重力场模型、格网等效水高等产品(Case, 2010). 在时变重力场解算过程中,常用的数据主要包括轨道数据GNV1B、加速度计数据ACC1B、星间距离测距数据KBR1B和卫星姿态数据SCA1B(Case, 2010).值得注意的是,由于卫星官方提供的轨道数据为动力学轨道GNV1B,其轨道过于平滑且包含了先验信息,可能会削弱时变信号的恢复能力(杨帆等,2017),推荐使用几何轨道数据参与解算.
重力卫星成功发射之后,由于卫星仪器本身存在一系列系统误差,且部分随机误差呈现与在轨环境相关的观测特性,除了需要通过在轨标定完成系统误差消除之外,还需要通过一系列的数据精细处理技术,以提高观测数据的精度水平(Wu et al.,2006). 自GRACE卫星成功发射以来,官方数据处理机构根据对载荷性能的深入认知,逐步修正观测数据中的未知噪声,先后发布了从V00~V03的四代观测数据. 在V01观测数据中,重点对遥测数据处理方法进行了改进;在V02观测数据中,重点改进了卫星质心标定方法、KBR相位中心标定方法、轨道解算方法和钟差解算方法;在V03观测数据中,重点对卫星姿态观测数据进行了重新处理,并对星间测距数据进行了进一步优化(Horwath et al., 2011; Inácio et al., 2015; PODAAC,2018). 如图3所示,采用精化后的星象仪观测数据,天线相位中心改正量显著减小. 每次数据精度的提升,都会推进时变重力场建模精度的提升.
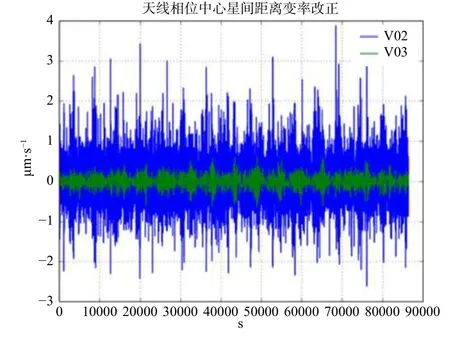
图3 不同版本星象仪数据计算的天线相位中心改正量(修改自Harvey and Sakumura, 2019)Fig. 3 Including angular acceleration measurements in V03 attitude solutions and eliminating the weighting error dramatically reduces antenna phase center correction noise, as evident in phase center range rate correction(modified from Harvey and Sakumura, 2019)
虽然经过多年GRACE卫星数据处理,国内外学者对于重力卫星数据处理积累了丰富的研究经验,但是GRACE Follow-On卫星发射之后,由于载荷特性、观测性能等方面的差异,重力卫星数据处理也面临全新的挑战. 例如,由于GRACE Follow-On卫星的一个加速度计无法工作,如何移植加速度计观测数据是当前的紧迫课题(Kim et al., 2015;Bandikova et al., 2019);为了提升时变重力场精度,如何充分融合多种类型的卫星姿态观测信息(Bandikova and Flury, 20144),并充分利用高精度激光测距数据信息(Abich et al., 2019; Kornfeld et al., 2019; Wegener et al., 2019; Yan et al., 2021),也是当前的热点研究问题.
1.4 摄动力模型的精化
由于重力卫星观测值中包含了卫星受到的所有力,包含保守力和非保守力. 在时变重力场建模过程中,非保守力可以利用星载加速度计精确测量,而保守力则需要利用先验模型进行扣除. 主要的保守力包括N体摄动、海洋潮汐、大气潮汐、固体潮汐、固体极潮、海洋极潮、大气海洋高频潮汐,以及相对论效应等. 由图4可知,在各类摄动力模型中,月球对卫星的引力量级最大,达到了10-6m/s2量级;以加速度计的10-10m/s2观测精度为阈值,除了其他行星对卫星的摄动力外,其他保守力摄动均需在建模中考虑(Lasser et al., 2020a).
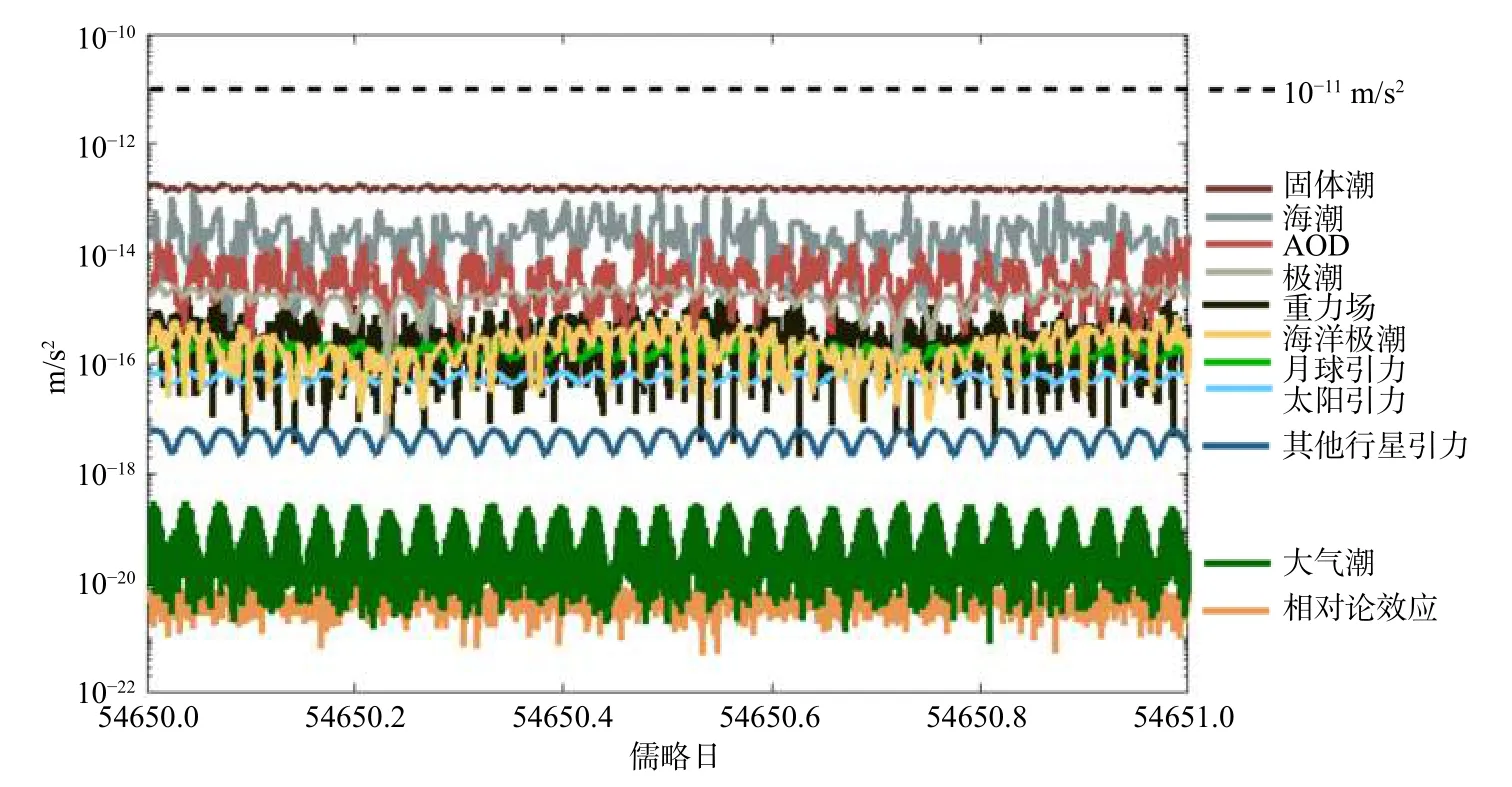
图4 各类摄动力模型的量级水平(修改自Lasser et al., 2020a)Fig. 4 Norm of the benchmark accelerations (modified from Lasser et al., 2020a)
高精度摄动力模型是实现时变重力场建模的重要前提,随着摄动力模型的精化,重力场建模的精度水平逐步提升. 例如,Reis和Desai(2017)更新了极潮的计算方法,各个机构采用该模型计算的C21项和S21项与SLR观测结果一致性显著提升(Save, 2018; Chen et al., 2021). 为了保障时变重力场精细建模,国际地球重力场联合组织COST-G发布了一天的保守力摄动数据(Lasser et al.,2020a),且各个机构与该数据的比对误差均小于10-10m/s2,为时变重力场建模提供了重要参考. 对于下一代重力卫星而言,随着载荷精度水平的提升,保守力摄动模型误差将是制约时变重力场建模的主要误差来源(Flechtner et al., 2016; Zhou et al.,2016),特别是海潮模型误差和大气海洋高频潮汐模型(即AOD模型)误差. 为此,国内外学者致力于发展高精度的保守力模型,如海潮模型产品已更新至FES2014(Lyard et al., 2021)和EOT20(Hart-Davis et al., 2021),AOD产品已更新至AOD RL06版本(Dobslaw et al., 2017). AOD RL06产品的截断阶次达到180阶,时间分辨率可达到3小时;而Yang等(2021)也采用欧空局最新发布的再分析数据,研制了分辨率为1小时的大气去混频产品.
1.5 时变重力场球谐解建模方法的改进
除了数据集和摄动力模型的优化,重力场建模方法的改进也是推进时变重力场精度提升的主要原因之一. 为了提升时变重力场球谐解的解算精度,各国学者致力于改进现有时变重力场建模方法.CSR、GFZ和JPL在历年的重力场解算过程中,不断改进各类参数设置对重力场建模精度的影响(Bettadpur, 2018; Dahle et al., 2018; Yuan, 2018).ITSG发现仅仅考虑加速度计对角线参数对低阶项解算有影响,而采用满阵的加速度计校准矩阵可显著减小系统误差,使得解算的C2,0系数项与SLR数据处理结果更为一致(Klinger and Mayer-Gürr,2016). AIUB和GRGS分别在发布原有重力场的基础上,更新了数据预处理策略,并顾及了部分系统误差的影响,先后发布了最新的时变重力场模型AIUB RL02(Lasser et al., 2020b)和CNES GRGS RL04(Lemoine et al., 2019).
随着对时变重力场建模过程的深入认识,我国学者也在建模方法改进方面有了突破性进展. 邹贤才等(2015, 2016b)发展了动力学法的同解法,可实现卫星轨道和重力场的同时求解. 陈秋杰等(2013)和Chen等(2015, 2016, 2019)创建了改进的短弧法,先后将轨道误差、星间距离变率误差、加速度计误差和星象仪误差等观测误差与重力场模型一并求解,并突破短弧法弧长较小的缺陷(如图5),最终发布了最新的时变重力场模型Tongji-Grace2018. Zhou等(2018, 2019, 2020a)重点对星间距离变率低频噪声处理方法和轨道耦合效应进行了改进(如图6),最终发布了最新的时变重力场模型HUST-Grace2019. Guo等(2018)利用依频率定权的方法有效顾及观测值有色噪声,显著提升了结果的精度水平(如图7),最终发布了最新的时变重力场模型WHU RL02.
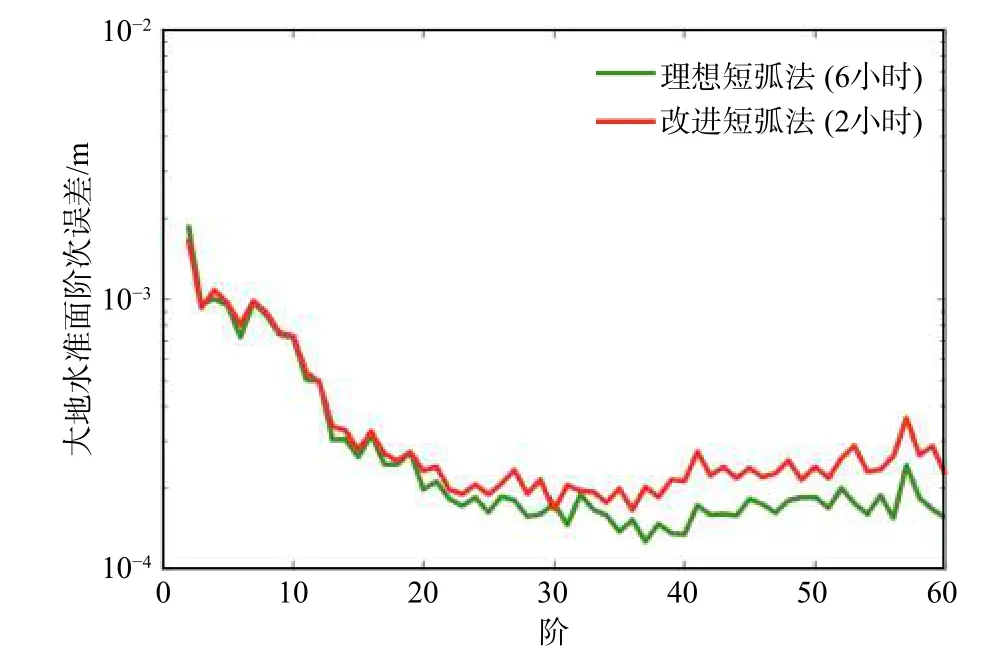
图5 改进短弧法的反演结果(修改自Chen et al., 2019)Fig. 5 Gravity field solutions in terms of geoid degree variances determined by using the modified (2-hr arcs)and optimized(6-hr arcs) short-arc approaches(modified from Chen et al., 2019)
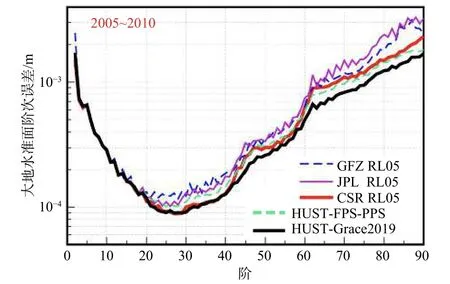
图6 改进动力法反演结果精度(修改自Zhou et al., 2019)Fig. 6 The geoid height per degree of GFZ RL05, JPL RL05,CSR RL05, HUST-FPS-PPS, and HUST-Grace2019.FPS = filtered processing strategy; PPS = pure predetermined strategy (modified from Zhou et al., 2019)
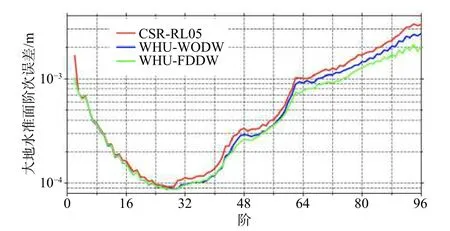
图7 顾及频域相关加权的反演结果(修改自Guo et al.,2018)Fig. 7 Geoid height differences per degree for different gravity field solutions derived from frequency-dependent data weighting (FDDW) scheme and the standard leastsquares adjustment without a data weighting (WODW)(modified from Guo et al., 2018)
随着观测数据的优化、摄动力模型的精化和解算方法的改进,时变重力场球谐解建模的精度也逐步提升. Save(2018)比较了得克萨斯大学空间科学中心CSR(Center for Space Research)发布的不同代重力场模型的精度水平(如图8),结果表明相对于发布的第一代产品RL01,最新发布的第六代产品RL06的精度水平提升了约20倍.
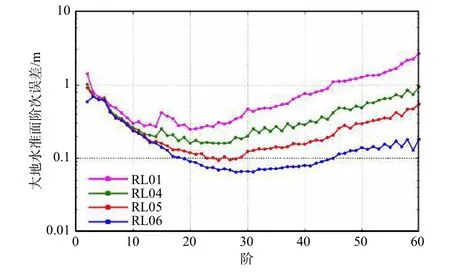
图8 不同版本CSR发布产品的精度水平(修改自Save,2018)Fig. 8 GRACE reprocessing history at CSR from RL01 to RL06 (modified from Save, 2018)
截止目前,国内外最新的时变重力场球谐解模型主要包括CSR RL06、GFZ RL06、JPL RL06、AIUB RL02、 HUST-Grace2020、IGG RL01、ITSGGrace2018、LUH-Grace2018、SWJTU Grace RL01、Tongji-Grace2018、WHU RL02以及XISM&SSTC GRACE01等. 图9给出了各个机构模型的大地水准面阶次误差,以综合分析不同模型的精度水平,结果表明:各家机构反演的时变重力场模型在低阶次部分较为一致,表明均反演出了长波段的时变信号;中高阶次部分精度各异,主要与各个机构采用的观测数据、摄动力模型和解算方法密切相关. 总体而言,我国各个机构解算的模型精度与国际机构解算精度水平相当,为推进我国自主重力卫星计划奠定了重要的理论基础和技术支撑.
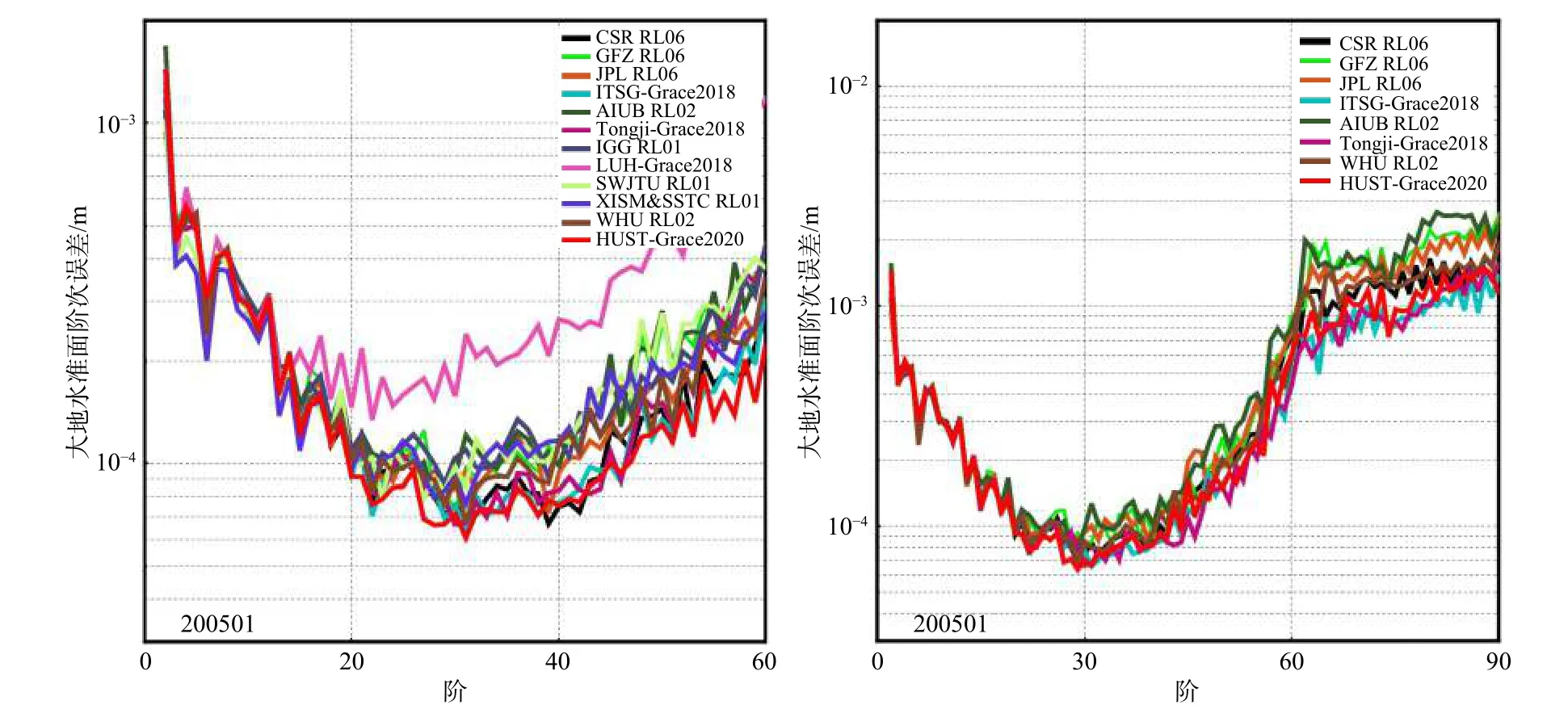
图9 不同机构发布最新版本时变重力场模型的精度(左图:90阶;右图:60阶)Fig. 9 Comparison of the newest temporal gravity field model from different institutions (left: degree 90, right: degree 60)
由于随机误差和未知噪声影响了时变重力场模型解算精度,各个机构解算模型存在一定差异. 为了联合各个机构的解算优势,瑞士伯尔尼大学正在推进时变重力场模型综合服务COST-G(the Combination Service for Time-variable Gravity field solutions),旨在实现多个机构模型的联合解算(Jäggi et al., 2019; Meyer et al., 2019). COST-G组织的欧方成员主要包括AIUB、ITSG、GFZ以及LUH,中方的武汉大学、中国科学院精密测量科学与技术创新研究院、南方科技大学和华中科技大学也作为核心成员参与其中,力求进一步提升全球时变重力场的精度水平.
2 高低卫星跟踪卫星确定时变重力场
受限于卫星轨道高度、定轨精度、非保守力模型精度等因素的综合影响,早期利用高低卫星跟踪卫星模式仅能够反演部分低阶次位系数的变化,难以获取高精度的地球重力场时变信息. 随着低轨卫星发射、定轨精度的提升以及高精度在轨加速度计的搭载,多颗低轨卫星也具备了时变重力场监测的能力. 例如,通过充分优化电离层改正、相位中心改正等定轨过程中的系统误差(Bock et al., 2011;Jäggi et al., 2015)、顾及轨道观测历元之间的相关特性(Jäggi et al., 2011),可利用高精度GOCE卫星轨道实现时变重力场建模(Jäggi et al., 2015).Bezděk等(2014)建立了改进的加速度法,并分别利用CHAMP、GRACE和GOCE卫星的几何轨道数据实现了时变重力场建模(如图10). 罗志才等(2015)通过充分考虑不同轨道方向观测值的频谱贡献,实现了顾及多方向观测值权比反演地球重力场的动力法. Guo等(2017, 2020)先后提出了基于历元差分观测值的重力场反演新方法,有效克服了观测值中的系统误差和非稳态噪声,显著改善了时变重力场反演精度.
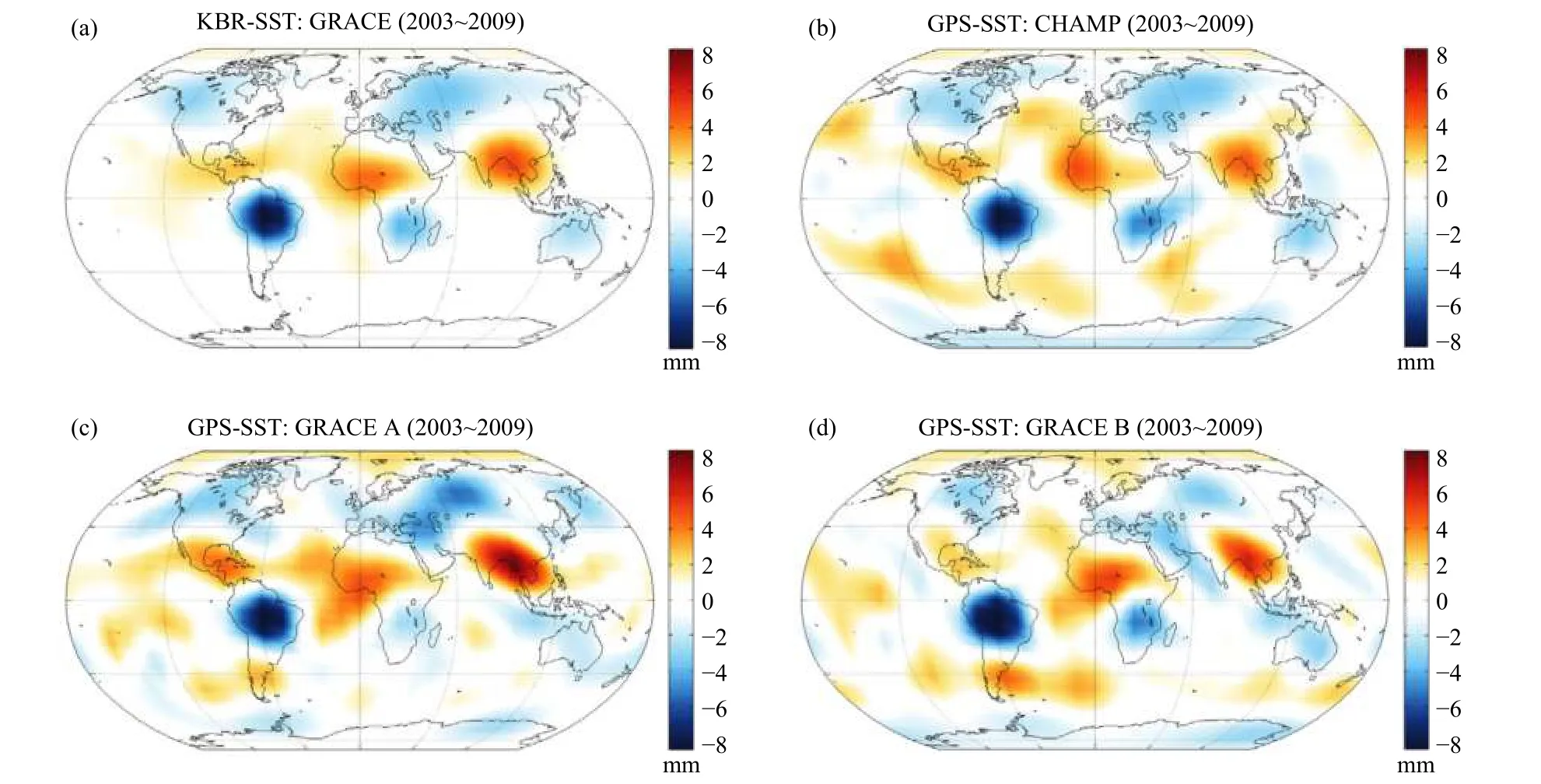
图10 高低跟踪数据反演时变重力场的空域结果(修改自Bezděk et al., 2014)Fig. 10 Average seasonal geopotential variation computed from: (a) GRACE KBR data (CSR RL04); (b)~(d) GPS positions of CHAMP, GRACE A/B satellites (modified from Bezděk et al., 2014)
由于卫星定轨精度仅为cm级,而星间测量精度可达到μm级甚至nm级,利用低低卫星跟踪卫星模式反演的时变重力场精度显著优于高低卫星跟踪卫星模式. 然而,低低卫星跟踪卫星模式具备专用性,不一定长时间存在在轨飞行卫星,如GRACE和GRACE Follow-On卫星之间存在约1年的观测空白期. 在这种情况下,利用高低卫星跟踪卫星确定时变重力场模型,仍然可以实现大型流域的时变信号探测(如图11). Lück等(2018)利用Swarm卫星轨道数据分析了海洋区域质量变化特性,并探讨了利用该数据填补GRACE和GRACE Follow-On卫星空白期的可行性,证实高低卫星跟踪卫星数据可为实现连续时变重力信号监测提供重要的技术保障. 特别地,通过类似于Swarm卫星等组网飞行模式,理论上可进一步提升高低卫星跟踪卫星探测时变信号的能力(Wang et al., 2011; Zhou et al., 2020b).
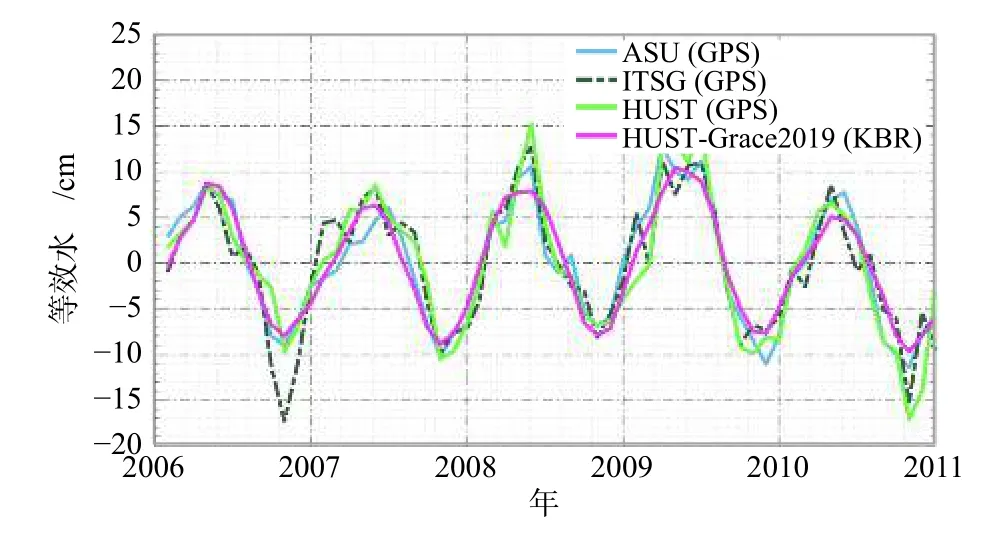
图11 高低跟踪数据反演时变重力场的时域结果(修改自Zhou et al., 2020b)Fig. 11 Terrestrial water storage variations in terms of EWH over Amazon River Basin derived from GRACE KBR monthly field, compared to the same quantities computed from GPS monthly fields. The maps are based on KBR/GPS monthly gravity fields from January 2006 to December 2010, limited to maximum spherical harmonic degree 15 with a Gaussian filter of 1 300 km radius (modified from Zhou et al., 2020b)
3 下一代重力卫星计划
受限于现有卫星编队模式、载荷噪声水平和背景力模型精度,现有时变重力场模型的精度和分辨率均有限(Flechtner et al., 2016; Zhou et al., 2016).为了进一步拓展时变重力场的应用,国内外学者致力于推进下一代重力卫星计划(姜卫平等, 2014;郑伟等, 2014, 2017; Pail et al., 2015; Zhao et al.,2021).
基于现有南北跟踪方式的轨道构型探测时变重力场时,不可避免地存在南北条带误差等系统性误差. 为了削弱这部分误差的影响,国内外学者也致力于研究全新的卫星编队构型. Lemoine等(2020)设计了基于中轨和低轨星间链路组合方式的MARVEL计划,同时实现地球重力场的精确测量和参考框架的精确构建;Panet等(2012)以钟摆轨道构型为基础,提出了e.motion计划;Wiese等(2012)提出了四星轮转编队,可显著提升重力场观测精度;Cesare等(2010)以GRACE构型为基础,提出了基于10 km基线长度的TAS-I计划;Zheng等(2015)给出了改进的GRACE任务计划,并分析了对应的核心载荷指标需求;Lévèque等(2021a)提出了GRICE计划,重点探讨了冷原子技术在下一代重力卫星计划中的应用前景. 除此之外,Elsaka等(2014)系统对比了7种不同的卫星构型探测时变重力场信号的能力,结果表明采用Bender构型反演时变重力场的精度最高(如图12). Bender构型包含了一组飞行在极地轨道上的卫星和一组飞行在倾斜轨道上的卫星,可在保障全球观测的同时,最大限度的引入东西向观测信息,从而提升时变重力场的监测能力(Wiese et al.,2012). 鉴于Bender构型的诸多优点,美国宇航局NASA(2018)正联合德国地学中心GFZ以该构型为基础,大力推进GRACE-I计划(Flechtner,2020),欧空局也一直致力于推进e.motion2计划(Gruber et al., 2016). 我国已于2021年成功发射重力卫星,将实现重力场完全自主观测;同时,正在推进以Bender构型为基础的天琴二号卫星,为引力波探测提供技术支撑的同时,积极谋划我国下一代重力卫星计划. 上述提及的重力卫星计划均以低低卫星跟踪卫星观测模式为基础,预期可为发展高精度高分辨率时变重力场提供新的机遇.
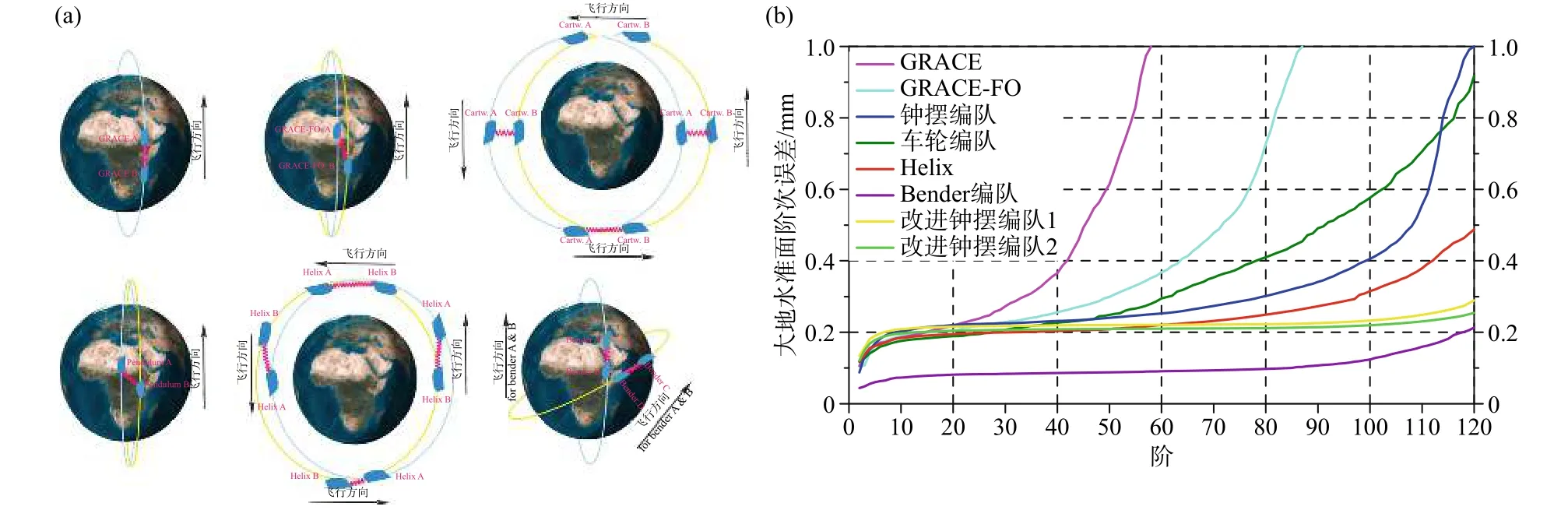
图12 不同的卫星轨道构型及其确定时变重力场的精度水平(修改自Elsaka et al., 2014)Fig. 12 The investigated FGM configurations, GRACE-reference, alternative GRACE Follow-on, Cartwheel, Pendulum, Helix and inline Bender (left), and the gravity solutions from the studied FGM scenarios in terms of cumulative errors of geoid heights(modified from Elsaka et al., 2014)
由于Bender卫星构型包含了四颗重力卫星,若由单一机构承担的经费压力较大;若由两家独立机构开展潜在合作,则需要保障观测系统的独立性. 对于一组极轨轨道,通过GRACE和GRACE Follow-On卫星已经证实了其观测能力;一组独立的倾斜轨道卫星会存在明显的极空白特性,即两极地区没有观测值覆盖,其获取观测时变信号的能力有待进一步验证. 鉴于此,Zhou等(2021)采用闭合仿真模拟方式详细研究了基于独立倾斜轨道观测数据确定地球重力场的可行性. 结果表明:倾斜轨道可实现观测区域内时变信号的精确监测,并提升观测区域内小流域、冰盖和地震区域时变信号的观测能力,预期可支撑两个机构或者单个机构备份式开展Bender构型的下一代重力卫星计划(如图13).
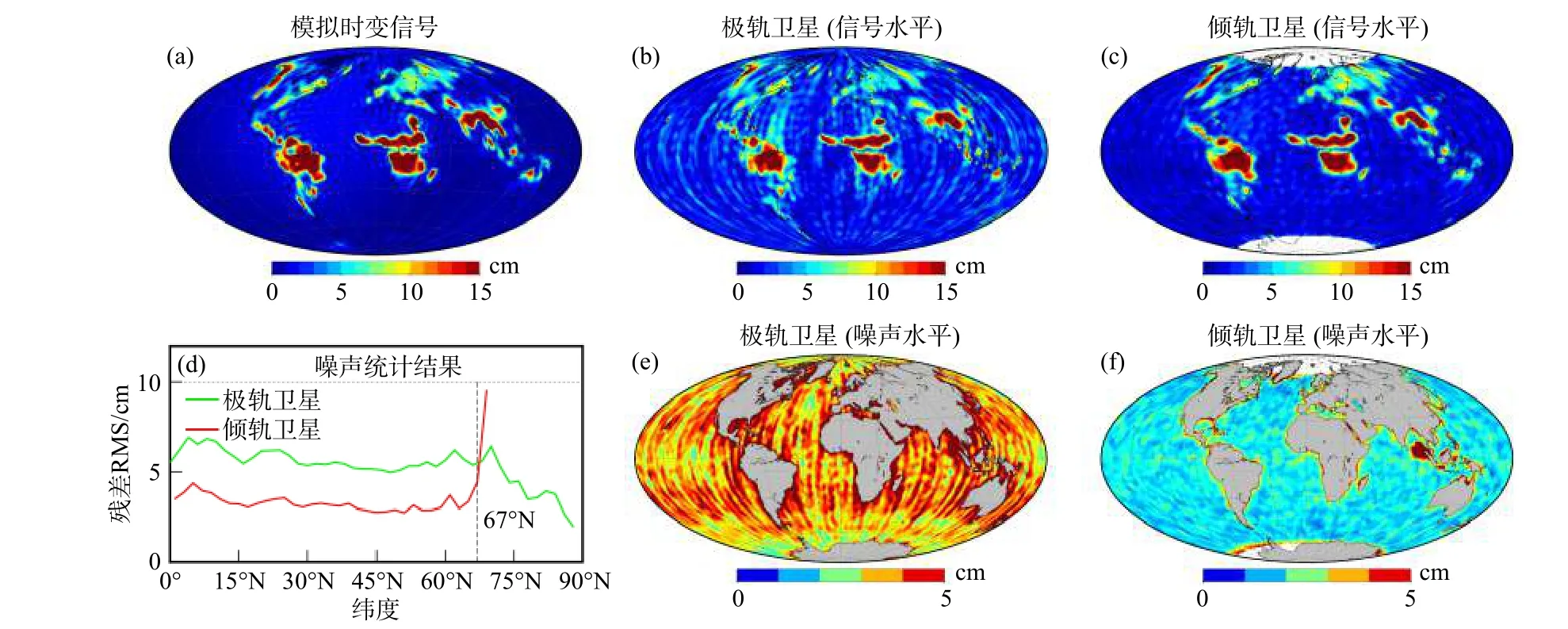
图13 独立倾斜轨道确定时变重力场的能力分析(修改自Zhou et al., 2021)Fig. 13 Annual amplitude (top) and RMS residuals (bottom) derived from ESM HIS model, polar satellite formation and inclined satellite formation (modified from Zhou et al., 2021)
除了低低卫星跟踪卫星模式之外,随着观测技术的发展,国内外学者也正在积极探讨其他观测模式下时变信号的探测能力. Wu等(2019)、Müller和Wu(2020)、Lévèque等(2021b)以及Schröder等(2021)先后探讨了在光钟观测能力提升的前提下,利用多种在轨飞行模式下搭载光钟探测时变重力场的能力. 结果表明,下一代光钟有望进一步提升时变重力场的观测精度.
4 总结与展望
时变重力场综合反映了地球系统的物质运移过程,在地球科学领域得到了广泛应用. 随着重力观测数据的累积与精化、背景力模型的优化以及解算方法的改进等,全球时变重力场的精度水平得到了明显提升. 尽管如此,现有时变重力场模型的精度和分辨率水平仍有进一步提升空间,主要体现在以下三个方面:
(1)重力卫星是一个复杂的观测系统,各类载荷受观测环境的影响较大,且载荷之间的相互耦合效应仍然是一大难题. 如何进一步提升原始观测数据的处理水平,是实现观测数据精化必须解决的关键科学问题.
(2)背景力模型的模型化误差难以量化,其对现有重力场建模精度的影响难以精确评估. 特别地,海洋潮汐模型、大气海洋去混频模型等先验模型的误差仍然较大,是制约下一代重力卫星计划发展的重要障碍,如何进一步提升背景力模型的精度,将是发展下一代重力卫星计划面临的紧迫课题.
(3)重力场建模方法虽然存在差异,但其本质上是一个最小二乘估计问题. 如何充分考虑建模过程中的系统误差和随机误差,是提升时变重力场建模精度亟待解决的科学问题.
利用重力卫星观测数据建立时变重力场过程中,不可避免地会面临卫星构型、观测噪声、背景力模型误差以及解算误差等综合影响,如何进一步克服上述问题仍然是当前的重要研究课题. 除了提升模型解算精度,国内外学者也在尝试利用新的解算形式,以期提升局部区域或者全球时变解的精度水平. 例如,为了水文、冰川、地震等领域学者使用方便,国际上先后发布了多种Mascon解算产品(Watkins et al., 2015; Save et al., 2016),且多个应用场景证实Mascon产品在局部地表质量监测中的优势(Luthcke et al., 2008, 2013; Zhang et al.,2020). 国内的李琼(2014)、苏勇(2015)、邹贤才等(2016a)等也先后利用卫星观测数据计算了全球或者区域Mascon解算产品,展现了该产品在全球或局部地区地表物质迁移的表征能力. 张岚和孙文科(2022)对重力卫星GRACE Mascon产品的计算方法、现有产品和应用情况进行了综合性论述. 由于Mascon解与约束条件的添加方式密切相关,各家机构发布的Mascon产品之间仍存在明显差异. 如何进一步统一Mascon解的解算过程并科学评估Mascon解的精度水平,是发展Mascon产品面临的重要问题.

