面向绝对重力测量的振动补偿技术发展

文 艺，伍 康*

1 清华大学 精密测试技术及仪器国家重点实验室，北京 100084

2 清华大学 精密仪器系，北京 100084

0 引 言

绝对重力测量在计量学、地球科学、资源勘探、军事等科学研究与工程技术领域都有着广泛的应用（Marson and Faller, 1986; Faller, 2003, 2005; 刘冬至等, 2007; Robinson and Kibble, 2007; 张为民等,2008），同时也为相对重力测量提供重力基准. 测量绝对重力值的仪器被称为绝对重力仪，目前国际上主流的是基于经典光学和原子干涉法两种测量原理的绝对重力仪（Timmen et al., 1993; Niebauer et al., 1995; Peters et al., 2001; 胡华等, 2012; Hu et al.,2013），测量精度可达微伽（1μGal = 1×10-8m/s2）量级.

无论是激光干涉还是原子干涉绝对重力仪，都需要为干涉测量提供一个稳定的惯性参考点. 实际测量中作为参考点的参考棱镜或平面镜容易受到振动噪声的影响，从而导致振动噪声耦合入干涉测量的落体运动轨迹中，影响重力加速度的精确测量.振动噪声的来源主要有两大类：环境噪声和仪器噪声（要佳敏和伍康，2019）. 环境噪声与周围环境、地点有关，频率分布范围广，其中低于0.05 Hz的环境振动噪声主要来自风湍流引起的气压波动，其强度较小，对绝对重力测量的影响可以忽略不计；0.05～1 Hz 的环境振动主要来源于地球脉动噪声，图1给出了不同地点的地脉动噪声竖直分量功率谱密度和全球新高低噪声模型（Trnkoczy et al.,2012），其中频率在0.3 Hz左右的地脉动噪声强度最大，该类噪声无法避免，是典型重力台站环境下的主要干扰噪声；1 Hz 以上的振动主要来自周围环境和人类活动，可以通过选择在远离人类活动频繁的区域、偏僻安静的地点进行测量来减少这部分噪声的影响（Haubrich and McCamy, 1969; Sorrells and Douze, 1974; Cessaro, 1994）. 仪器噪声则主要由重力测量期间，仪器自身传动机构所产生的噪声，如激光干涉绝对重力仪中的反冲振动（Rothleitner et al., 2009; Niebauer et al., 2011），该类噪声频率相对较高，且相位重复性高，导致重力测量结果产生系统偏差. 从噪声源的频率、相位和强度三方面分析，振动噪声对重力测量的影响的波动范围从微伽量级到几十毫伽量级，因此振动噪声的处理技术是目前限制绝对重力测量精度的主要瓶颈.

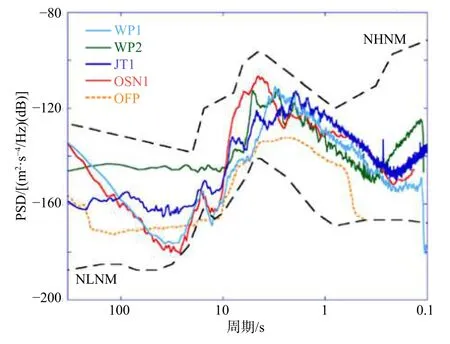
图1 地脉动噪声模型的加速度功率谱密度Fig. 1 Acceleration power spectra of seismic ambient noise

目前，绝对重力测量领域常用的两种处理振动噪声的方法为：垂直隔振和振动补偿. 前者通过具有超低本征频率（通常小于0.1 Hz）的垂直隔振系统来衰减竖直方向上参考棱镜所受的振动噪声, 后者则通过传感器探测参考棱镜所受的振动噪声，并利用探测结果对落体轨迹进行修正.

1 振动补偿应用背景

超低频垂直隔振技术发展历史悠久，自1934年发展至今，已经可以实现微伽量级的隔振效果，满足高精度绝对重力测量的需求，但是由于隔振系统的抗干扰能力较差，多用于台站、实验室等安静环境中进行地面静态绝对重力测量. 振动补偿的思想最早于20世纪末期被提出，现有的振动补偿系统能实现毫伽至几十微伽的补偿效果，效果尚不如隔振，但由于振动补偿系统结构简单，抗干扰能力更好，可应用于野外等更加复杂的地面静态测量环境以及船载等动态测量环境.

振动补偿技术的发展，使测量精度优于毫伽量级的小型化高机动性绝对重力仪的实现成为可能.由于绝对重力仪消除了相对重力仪的测值漂移效应，无需经常回到基站进行标定，在野外流动重力观测和海洋/航空重力测量中的应用需求日益增加，在现代国防领域、资源勘探领域、地球科学领域有着广阔的应用前景.

2 振动补偿研究现状

多年来，国内外多个课题组对振动补偿技术进行了大量研究，从实验室等静态测量环境下的振动补偿研究逐渐发展到船载等动态测量环境下的振动补偿研究，下文将分两部分进行详细介绍.

2.1 静态重力测量中的振动补偿技术

中国计量科学研究院早在1980年代就开始探索新的处理地面振动噪声的方法，郭有光等（1988）研制的NIM-II型激光干涉式绝对重力仪利用地震计探测干涉仪中参考棱镜的运动，如图2所示，并提出振动划线的方法来进行振动补偿（Wu, 2011;龙剑锋等, 2012）. 该方法中地震计的测量数据并非直接用于下落轨迹的修正，而是用于对下落轨迹测量数据进行挑选. 通过对地震计的测量数据进行平行线扫描，选取落体下落轨迹上受到的振动影响为线性的时间、位移数据对，依据直线二次微分为零的数学原理，对选取的时间位移数据对进行二次拟合得到绝对重力加速度值，振动干扰量就会被抑制和消除，从而实现振动误差的抑制. 实际实验样机在国家重力基准点的测量结果显示补偿后测量精度提高了一倍（龙剑锋等，2012），说明该方法对消除振动干扰有效，但该方法补偿后对系统偏差无明显改善作用，且在不同地基条件下补偿精度水平不一，有待进一步分析改进.

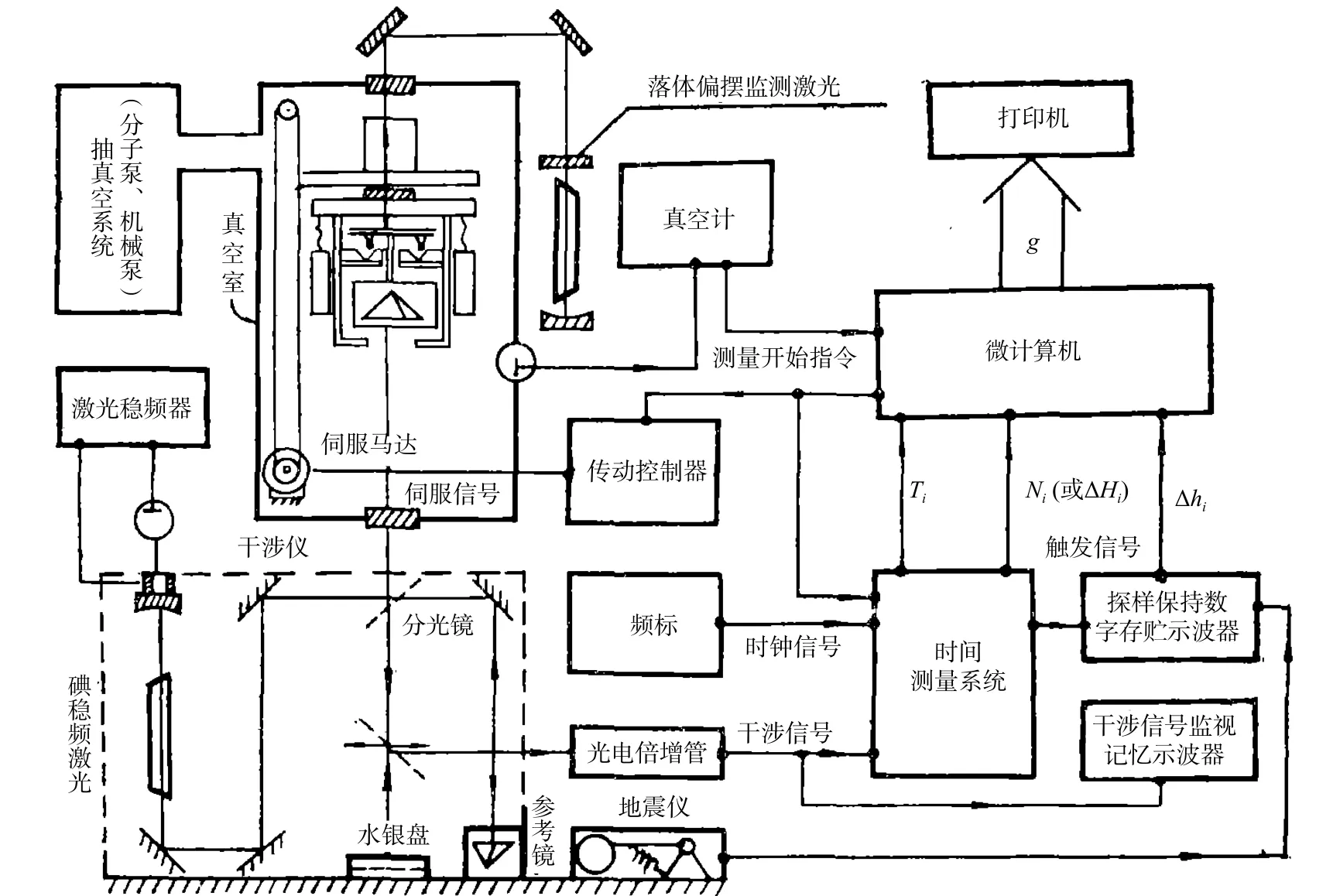
图2 NIM-II型绝对重力仪方框图（郭有光等，1988）Fig. 2 Block diagram of NIM-II absolute gravimeter （Guo et al., 1988）

Canuteson等（1997）在利用绝对重力仪对地震计STS-2进行传递函数标定的研究中，发现利用地震计进行地面噪声修正的可能性. 整个实验系统结构如图3所示，采用Fabry-Perot光纤干涉仪，将光纤固连在地震计的外壳上，地震计和干涉仪分别同时测量地面振动噪声以及下落棱镜相对地震计的下落轨迹. 对地震计输出信号直接利用其标称传递函数反推出相应的振动位移，再通过后处理修正原始下落轨迹得到补偿后的测量结果. 实验室环境下的测试结果表明，单次测量的下落轨迹拟合残差标准差从补偿前的19 nm降低至4 nm，33次测量结果的标准差从补偿前的922 μGal降低至312 μGal（Canuteson et al., 1997）. 该系统验证了地震计振动补偿的有效性，利用地震计传递函数求解干涉测量参考点的振动噪声也成为一种经典的振动补偿方法. 然而由于地震计传递函数易受环境变化和仪器自身漂移影响而改变，该方法需要定期校正传递函数，补偿过程复杂. 此外，该方法没有考虑地震计传递函数以外的其它环节的传递函数，因此补偿效果不是很理想.

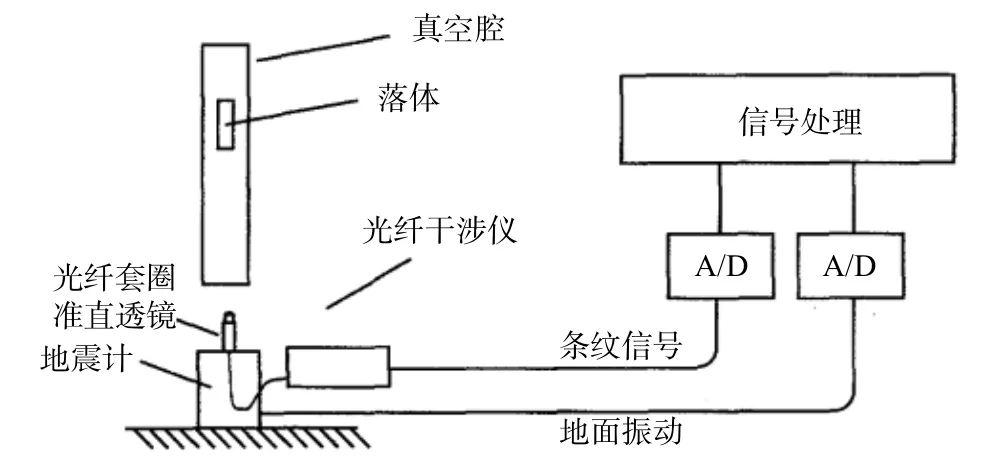
图3 基于绝对重力仪的地震计标定系统（修改自Canuteson et al., 1997）Fig. 3 Scheme of seismometer calibration system using a modified absolute gravimeter （modified from Canuteson et al., 1997）

Brown等（2001）提出了面向动态重力测量的振动补偿方法. 将激光干涉式绝对重力仪FG5的隔振系统替换为振动补偿系统，如图4所示，使用低噪声地震计Lennartz LE-3D作为传感器放置在参考棱镜附近并测量下落过程中的振动噪声，Brown等人假设地震计的输出信号相比参考棱镜的运动信号仅相差一个时延，时延通过遍历法以修正后拟合残差标准差最小为优化目标得到. 实验室环境下的静态测量结果表明，该振动补偿系统将离散度从补偿前的 ± 500 μGal降低至 ± 65 μGal，测量精度提高了约7倍，取得了一定的补偿效果（Brown et al.,2001）. 同时该方法将地震计输出信号和参考棱镜运动信号间的传递函数简化为一个纯时延环节，时延参数在测量中实时求解，可以实现实时的振动补偿. 然而该方法未考虑输出信号和参考棱镜运动信号的幅值关系，补偿效果仍存在提升空间.

图4 Brown提出的面向动态绝对重力测量的样机FgLS（Brown et al., 2001）Fig. 4 The FgLS Prototype Dynamic System proposed by Brown （Brown et al., 2001）

Brown提出的基于地震计振动补偿技术的初代样机逐步发展成型为商用小型化绝对重力仪FG5-L. Baumann（2003）采用FG5-L系统进行实验室环境下的振动补偿测试，系统结构如图5所示，采用周期为5 s的Lennartz LE-3D地震计作为振动传感器. 引入地震计测量噪声的下落轨迹拟合公式如式（1）所示：

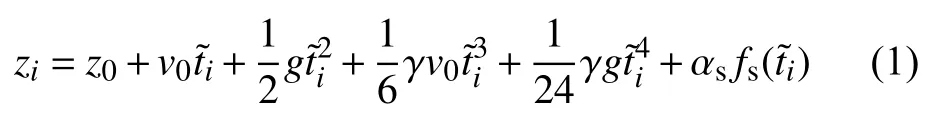
图5 绝对重力仪FG5-L（修改自Baumann, 2003）Fig. 5 Absolute Gravimeter FG5-L （modified from Baumann,2003）

式中，fs对应传感器的测量信号，αs对应传感器测量信号的标度因子. 传感器测量信号与下落测量轨迹的同步通过相关性分析实现，标度因子通过最小二乘法拟合得到. 实验结果表明，单次测量的下落轨迹拟合残差幅值从补偿前的±50 nm降低至±3 nm，补偿后的单次测量标准差为400 μGal，测量精度提高了约8倍（Baumann, 2003）.

2016年，Wang等（2017）对传感器输出信号和参考棱镜真实运动之间的关系进行了理论分析，将其分解成多个传递函数，如图6所示. 其中Ga为地面振动到参考棱镜运动的传递函数，Gb为地面振动X0到传感器输入的传递函数，Gc为传感器的传递函数.

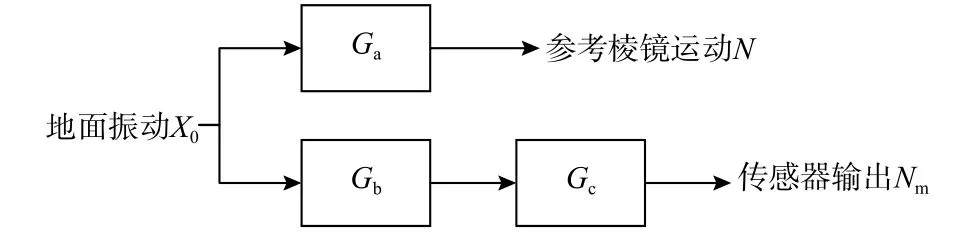
图6 传感器输出与参考棱镜运动的关系Fig. 6 Relationship between the output of sensor and the motion of reference retro-reflector

考虑到地震计传递函数在其带宽内的平坦响应、参考棱镜和传感器相邻放置的安装方式，以及实际中受环境影响出现的增益漂移情况，Wang等（2017）将两者之间的传递函数简化为增益延时环节，即：

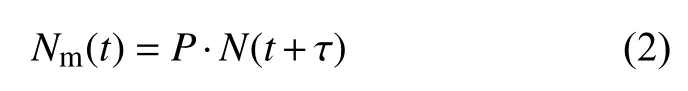
并通过理论分析与仿真，验证了传感器测量信号的拟合残差与下落测量轨迹的拟合残差具有高度相关性，以此为依据对两者进行相关分析来求解延时τ；再采用遍历法求解增益P，使得修正后轨迹信号的拟合残差的标准差最小. 采用Guralp公司的CMG-3ESP 型三分向宽频带地震计在实验室环境下进行振动补偿实验（图7），实验结果表明单次测量标准差由补偿前的5 141 μGal降低至242 μGal，且修正后的均值更接近真实值，验证了振动补偿方法的良好效果（Wang et al., 2017）. 在此基础上，Qian等（2018）提出了采用二维黄金分割法求解增益P和延时τ，本质上是一种遍历法. 该方法通过同时对增益—延时对（P,τ）进行遍历使得修正后轨迹信号的拟合残差的标准差最小（Qian et al.,2018）. 与Wang等（2017）提出的方法相比，黄金分割法可以实现相同的振动补偿效果，但大大减小了计算量，缩短了振动补偿时间.

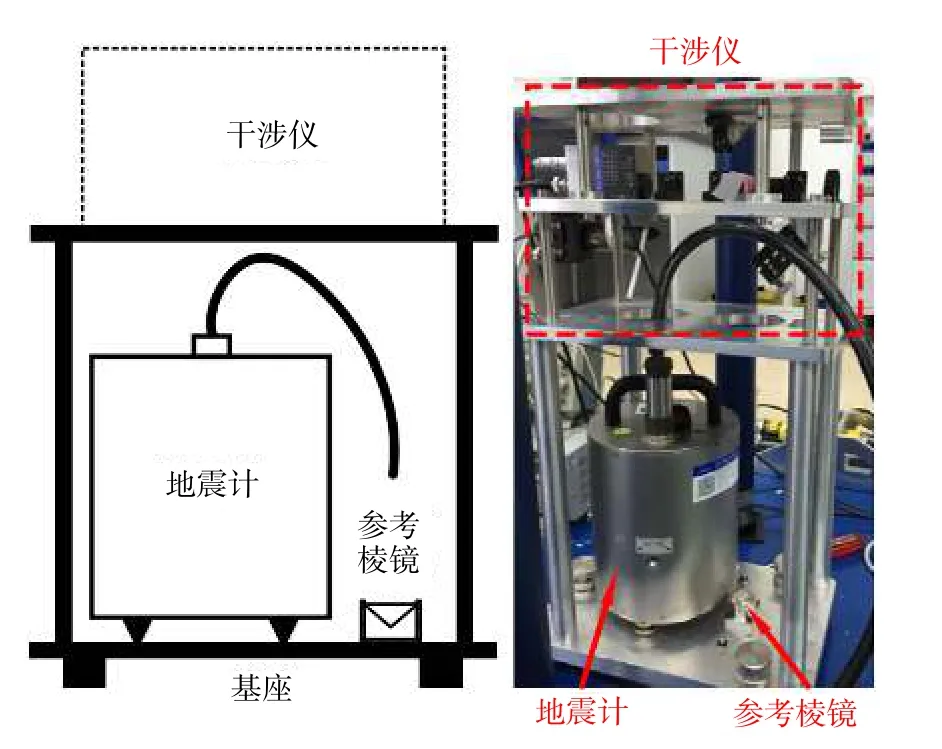
图7 王观等采用的振动补偿系统示意图和实物图（修改自Wang et al., 2017）Fig. 7 Schematic and physical diagram of vibration correction system adopted by Wang （modified from Wang et al.,2017）

之后，Wen等（2019）进一步理论分析了Wang等（2017）采用时延增益简化模型进行振动补偿的局限性，并针对地震计带宽较窄的问题提出了两种优化地震计振动补偿性能的方法. 第一种方法是利用基于卡尔曼滤波的多传感器数据融合方法，融合地震计和加速度计的测量数据，来获得兼有高精度和宽频带的振动信号，如图8所示，将地震计和加速度计同时放置在参考棱镜附近组成多传感器振动补偿系统，实验室安静环境下的测试结果表明，采用融合振动补偿方法可以将补偿性能提升13%（Wen et al., 2019）. 第二种方法是在采用单个地震计进行振动补偿的基础上，对地震计测量数据进行IIR后处理校正，再将校正后的数据代入进行振动补偿，该算法从数字上拓宽了地震计的带宽，可以得到更接近真实地面振动的测量数据（图9）.在安静环境和嘈杂环境下对该优化算法进行了实验验证，实验结果表明优化补偿算法在安静环境下将补偿性能提升26%，在嘈杂环境下将补偿性能提升56%（Wen et al., 2021）. 为提高振动补偿系统的动态性能，文艺等（2021）采用JN06D型加速度计代替地震计进行振动补偿，如图10所示. 实验证明，在高振动强度的万向悬架环境下，加速度计振动补偿可以将系统偏差修正1 000 mGal以上，将单次测量标准差改善13倍（图10）.

图8 文艺等采用的多传感器振动补偿系统示意图和实物图（修改自Wen et al., 2019）Fig. 8 Schematic and physical diagram of multi-sensor vibration correction system adopted by Wen （modified from Wen et al., 2019）

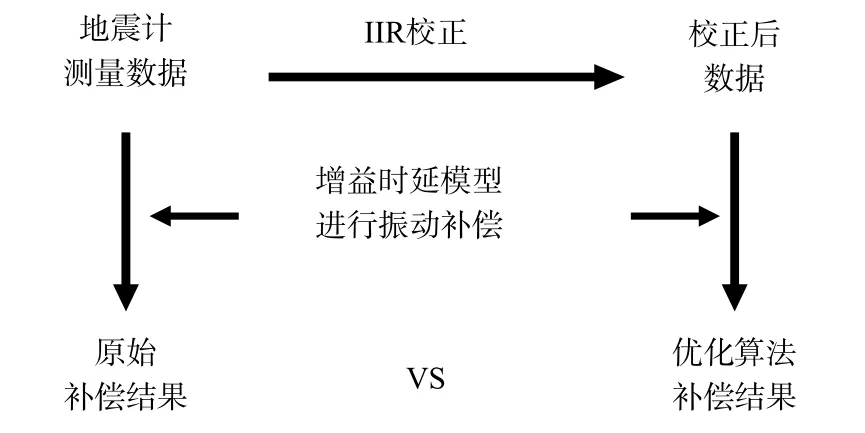
图9 基于IIR后校正的振动补偿算法流程Fig. 9 Scheme of the vibration correction algorithm based on IIR filter

图10 采用加速度计在万向悬架上作振动补偿实验（文艺等，2021）Fig. 10 Vibration correction experiment on a gimbal suspension using accelerometer （Wen et al., 2021）

此外，随着原子干涉技术的发展，许多原子干涉式绝对重力仪也采用类似的振动补偿方法处理振动噪声，通过商用传感器测量放置在其上方的反射镜的运动，计算振动噪声对干涉测量参考点相位的影响，其中以法国巴黎天文台（LNE-SYRTE）机构的研究成果为代表. Le Gouët（2008）、Le Gouët等（2008）、Merlet等（2009, 2010）将地震计Guralp T40放置在被动隔振平台Minus-K上，实现振动补偿与被动隔振的组合，如图11所示. 地震计的振动补偿有两种实现方式：一种是后处理补偿，对地震计采集信号进行滤波处理得到真实的反射镜运动信号，再最终进行相位修正，如图12a所示；另一种是实时补偿，通过闭环控制调整激光相位，使激光相位与平面镜造成的相位之和为零，如图12b所示（Le Gouët, 2008）. 在后处理补偿中，研究了两种滤波器：一种是采用递归IIR滤波器和非因果低通滤波器相结合，可以较好地补偿地震计传递函数，实验结果表明滤波后补偿的振动抑制效率与地震计数据直接补偿相比提升25%，提升效果受限的可能原因是水平运动的交叉耦合（Le Gouët et al., 2008）；另一种是纯时延校正，将地震计输出信号进行时移来补偿地震计传递函数引起的相移，时延校正补偿得到的振动抑制效率曲线与前一种方法不一样，但两种方法计算得到的相移与干涉仪跃迁概率间的相关系数相似. 此外，实验结果表明在外界振动较大时振动补偿效果更明显，振动补偿使得原子重力仪可以在超出其线性范围的情况下工作，并保持较高的测量灵敏度（Merlet et al., 2009），这体现了振动补偿技术在复杂环境下的应用潜力.2014年，该课题组Merlet利用Titan加速度计进行实时振动补偿，获得了约60倍的振动抑制效率（Lautier et al., 2014）.

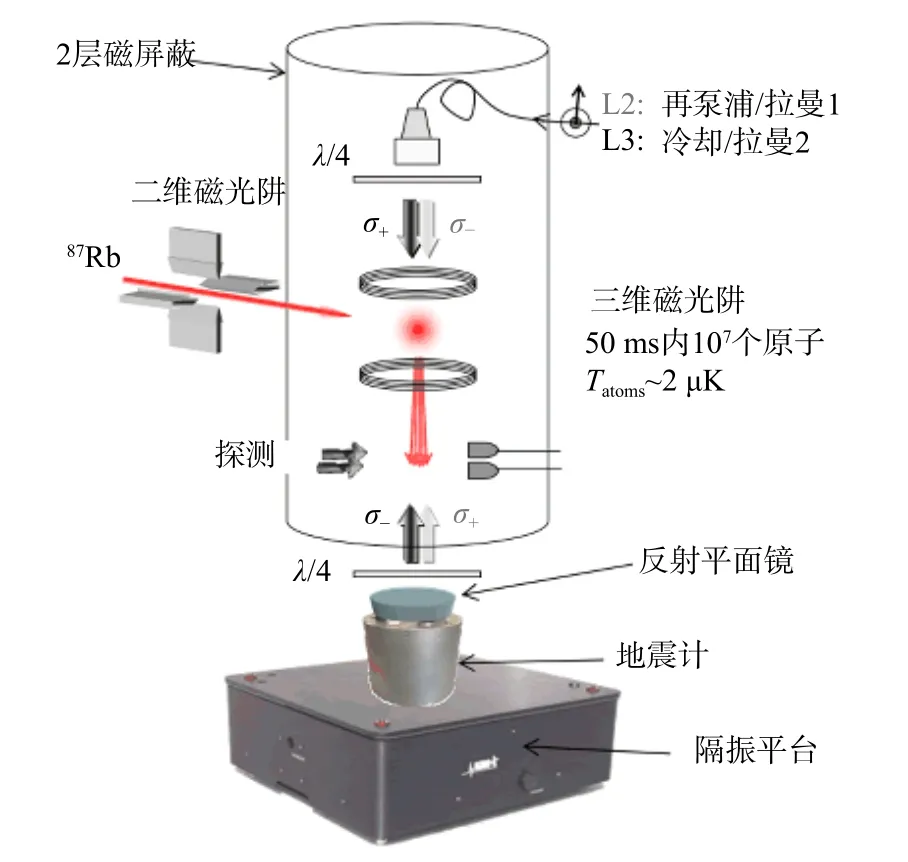
图11 地震计与被动隔振平台组合的振动补偿系统（修改自Le Gouët et al., 2008）Fig. 11 Vibration correction system of combination of seismometer and passive vibration isolation platform（modified from Le Gouët et al., 2008）

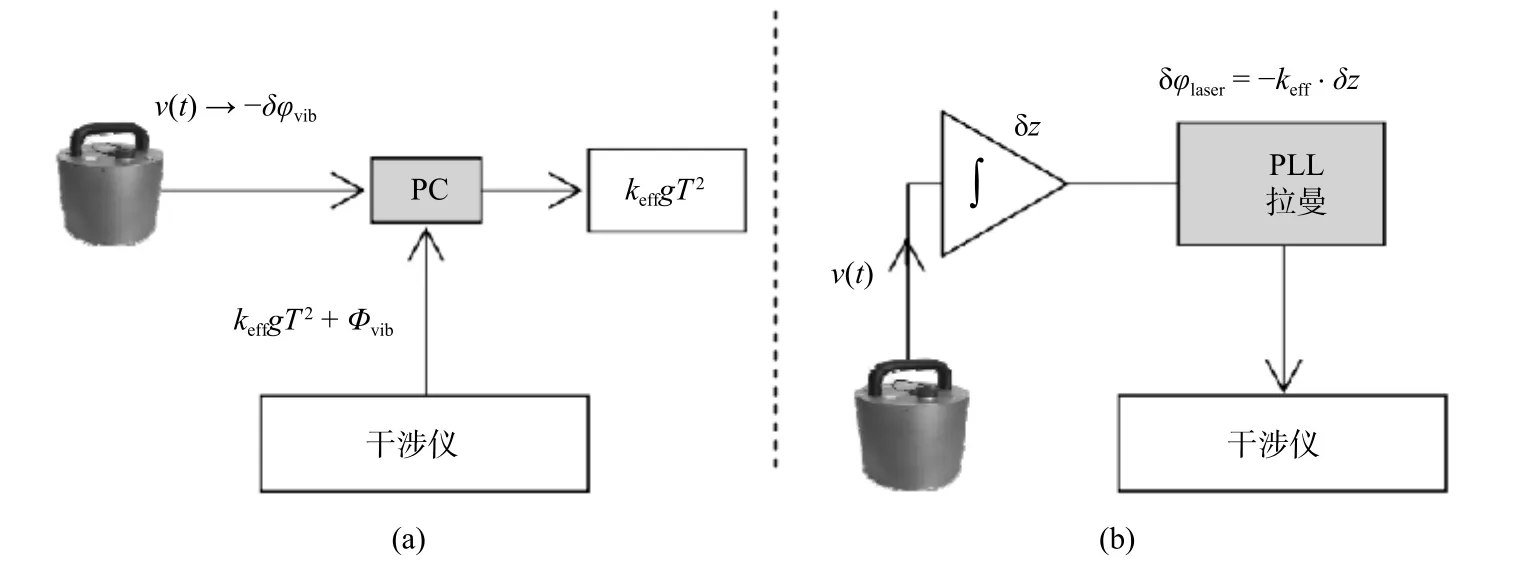
图12 （a）后处理振动补偿系统和（b）实时振动补偿系统示意图（修改自Le Gouët, 2008）Fig. 12 Diagrams of （a） the posteriori vibration correction set-up and （b） the real-time vibration correction set-up （modified from Le Gouët, 2008）

国内方面，浙江大学在原子干涉重力测量的振动补偿方面也进行了大量的研究. 许翱鹏等（2015）研究了振动补偿方法在恶劣振动环境下的噪声抑制效果，同样采用滤波修正法将传感器的输出信号转换为参考棱镜的运动信号，补偿流程如图13所示.进一步研究了滤波器的设计，通过给补偿系统施加激励，测量地震计输出到拉曼反射镜运动之间的传递函数，并提出两种滤波器设计方案：一种是直接设计一个与测量得到的传递函数相反的数字滤波器，由于传递函数过于复杂最终未能实现；另一种是对采集到的波形进行FFT，获得振动的频谱，将频谱经过测量得到的传递函数修正再用IFFT反演回时域波形，该方案最终通过购买商用计算软件实现，实现框图如图14所示. 实验结果显示振动补偿法的结果比补偿前有量级上的提高，但比被动隔振效果差了约一倍. 而在外界振动较大时振动补偿的结果更好，可以将大于4π的振动噪声引起的相位补偿回来，同时对每一个振动频率都有很好的优化（许翱鹏，2016）.

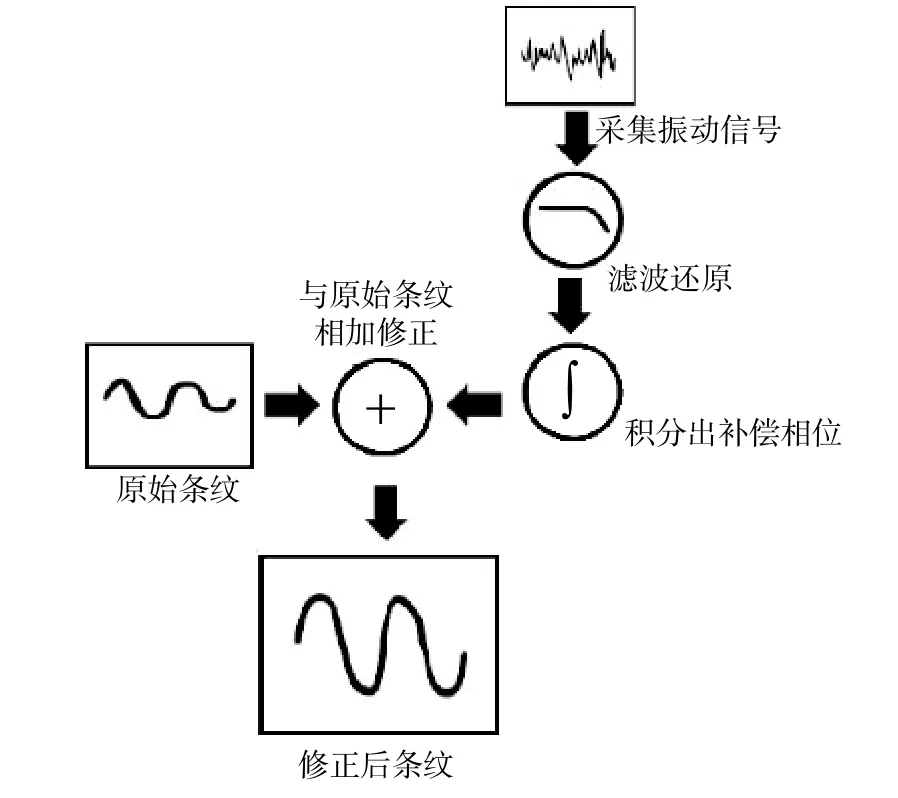
图13 许翱鹏等采用的振动补偿方案 （许翱鹏等，2015）Fig. 13 Vibration correction method adopted by Xu （Xu et al.,2015）

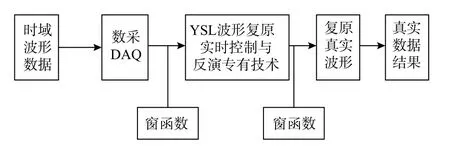
图14 传递函数控制反演的YSL方法（许翱鹏，2016）Fig. 14 YSL method of transfer function control inversion （Xu,2016）

由于传感器输出到干涉测量参考点运动之间的真实传递函数复杂、且难以标定， Araya等（2013）提出了一种将参考棱镜直接作为传感器敏感元件的振动补偿系统，系统结构如图15所示，参考棱镜由弹簧支撑，检测其相对地面的运动，反馈控制使参考棱镜跟踪地面振动，反馈电压可以直接反映参考棱镜的运动. 参考棱镜运动与反馈电压之间的灵敏度采用统计法进行标定，连续测量多次重力加速度用不同的灵敏度进行振动补偿，补偿后重力加速度的标准差最小时即可确定灵敏度. 此方法结合TAG-1型激光干涉式绝对重力仪，在日本东京大学地震研究所的雾岛火山观测站（KVO）进行连续测量，一天的测量不确定度为0.8 μGal （Araya et al., 2013）. 但是该系统带宽较低，只有DC～4 Hz，针对更复杂的振动环境，其补偿性能仍有待提高.

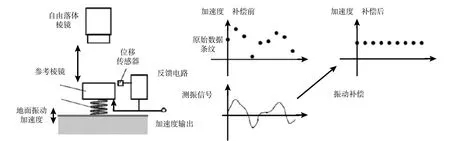
图15 Araya提出的振动补偿方法（修改自Araya et al., 2013）Fig. 15 Vibration correction method proposed by Araya （modified from Araya et al., 2013）

Guo等（2021）研制了一套基于内置棱镜式地震计的振动补偿系统，如图16所示. 参考棱镜作为地震计的敏感元件，固定在惯性质量块（机械摆体）上. 地震计采用电容换能器检测机械摆体相对地面的位移并输出差分电容；电容检测电路将差分电容转换为电压信号，作为系统的误差信号；该误差信号输入至反馈控制环节中，使得音圈电机驱动机械摆体跟踪地面振动. 反馈电压可以反映地面振动以及参考棱镜的运动. 该系统的带宽达到71 Hz，在实验室环境下连续测量25 小时，可以实现良好的潮汐跟踪，并达到10 μGal的测量不确定度（Guo et al., 2021）.

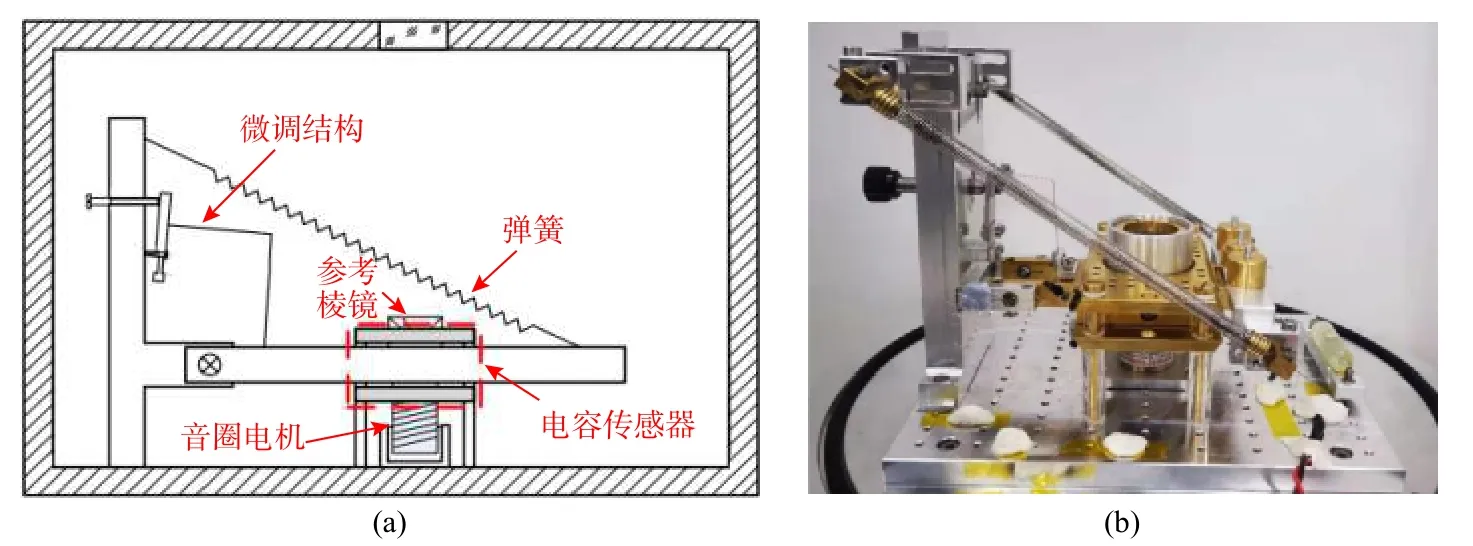
图16 内置棱镜式地震计.（a）结构简图；（b）实物图（修改自Guo et al., 2021）Fig. 16 （a） Schematic of the mechanical structure, and （b） photograph of the vertical seismometer with a built-in retroreflector（modified from Guo et al., 2021）

静态绝对重力测量中的振动补偿技术进展，汇总在表1 中.

表1 静态绝对重力测量中的振动补偿进展汇总Table 1 Overview of vibration correction technology in static absolute gravimetry

2.2 动态重力测量中的振动补偿技术

为实现面向移动平台测量环境的小型化高机动性绝对重力仪，采用动态性能更好的加速度计代替地震计作为振动传感器. Baumann等（2003）利用激光干涉式绝对重力仪搭建航空绝对重力测量系统，采用加速度计Episensor进行振动补偿，针对更加复杂的振动环境，改进补偿所用的下落轨迹拟合公式，如式（3）所示，额外引入了4个扰动，fj为第j个扰动信号的频率，与下落轨迹拟合残差的频谱中幅值最大的4个频率相对应：

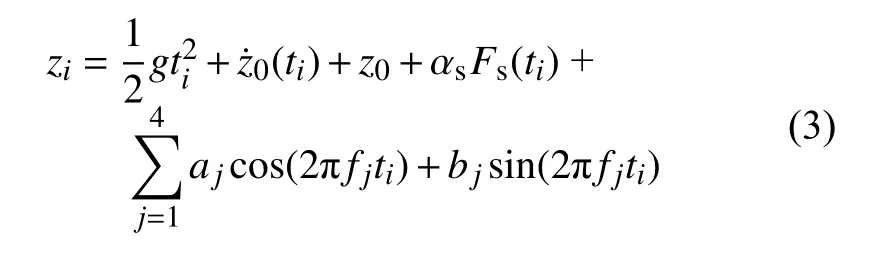
补偿过程分两步，首先针对单次下落数据利用改进后的拟合公式进行振动补偿，再对整个测量过程中拟合得到的重力加速度值，利用加速度数据进行整体补偿. 实验结果表明，该系统在实验室环境下的测量标准差为2.3 mGal，车载定点测量标准差为3.5 mGal，车载动态测量标准差为16 mGal，机载动态测量标准差为9.7 mGal（Baumann, 2003,2012）. 图17为采用加速度计Episensor振动补偿的机载绝对重力仪.

图17 采用加速度计Episensor振动补偿的机载绝对重力仪（修改自Baumann, 2003）Fig. 17 Airborne absolute gravimeter using accelerometer Episensor for vibration correction （modified from Baumann, 2003）

2018年，法国航空航天实验室利用原子干涉式绝对重力仪和两轴陀螺稳定平台，搭建了船载和机载绝对重力测量系统，系统结构如图18所示，拉曼反射镜放置在加速度计上，利用Q-Flex加速度计帮助锁定原子干涉仪的输出值，实现动态环境下的绝对重力测量. 实验结果表明该系统可实现优于1 mGal的船载测量精度和1.7～3.9 mGal的机载测量精度（Bidel et al., 2018, 2020）.

图18 船载原子绝对重力仪的振动补偿系统（修改自Bidel et al., 2018）Fig. 18 Vibration correction system of ship-borne cold atom gravimeter （modified from Bidel et al., 2018）

2021年，浙江工业大学则采用课题组较为成熟的小型化原子重力仪，利用加速度计采集拉曼反射镜的振动加速度来帮助还原原子干涉条纹，从而拟合得到精确重力加速度，如图19所示. 该系统可实现野外船载系泊状态下16.6 mGal/Hz-1/2的测量灵敏度和0.13 mGal的测量精度（程冰等，2021）.

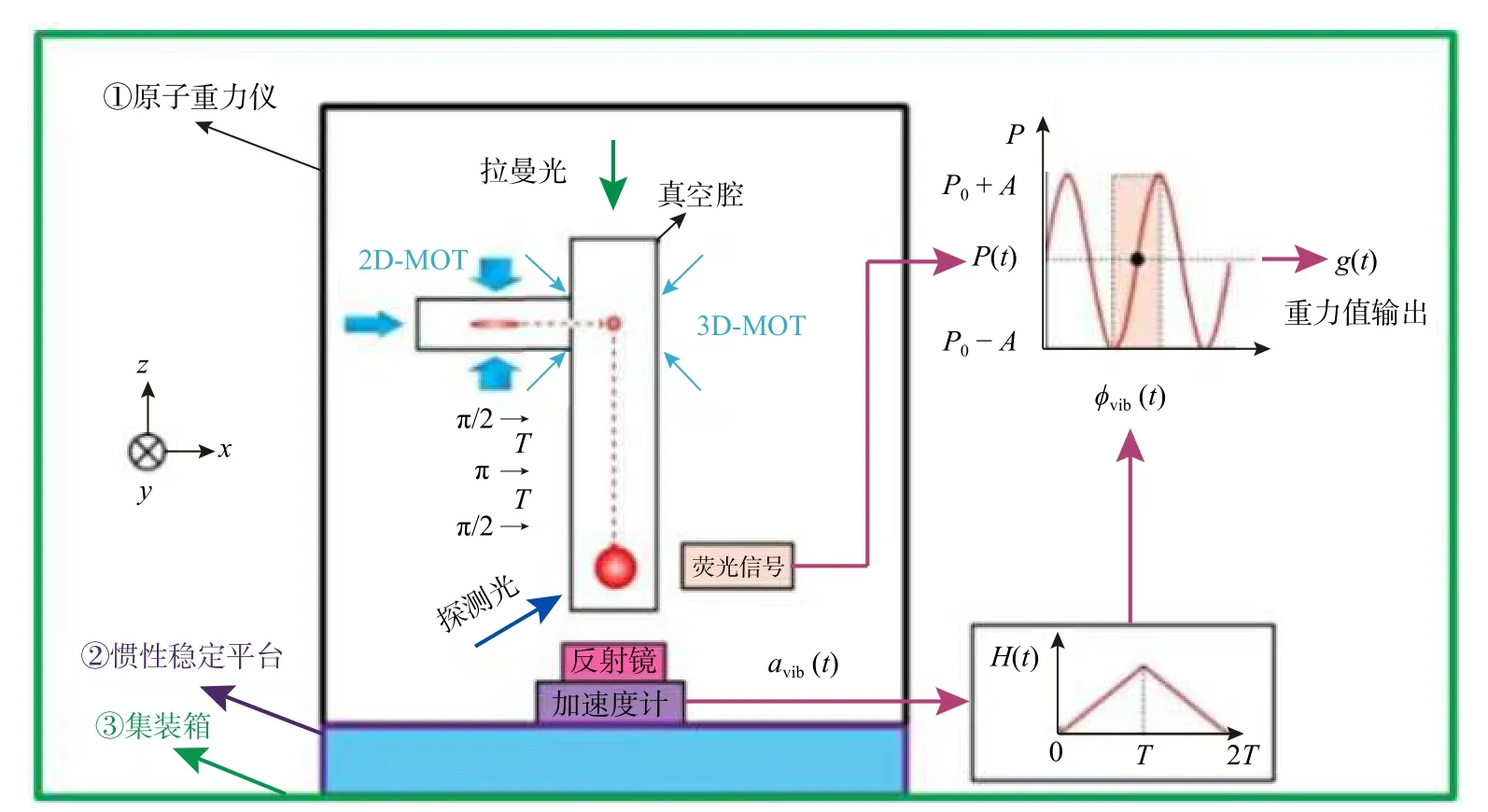
图19 船载系泊状态下的绝对重力测量系统原理图（程冰等，2021）Fig. 19 The schematic diagram of absolute gravity measurement system under mooring state of a ship （Cheng et al., 2021）

动态绝对重力测量中的振动补偿技术进展汇总在表2中.

表2 动态绝对重力测量中的振动补偿进展汇总Table 2 Overview of vibration correction technology in dynamic absolute gravimetry

3 振动补偿发展趋势

图20展示了近几十年振动补偿的发展情况，可以看到振动补偿技术正朝着适应高动态测量环境的方向发展. 随着小型化绝对重力仪在野外定点观测以及海洋/航空重力测量的广泛应用，未来将进一步对振动补偿系统的补偿精度、补偿速率以及动态性能提出更高的要求.

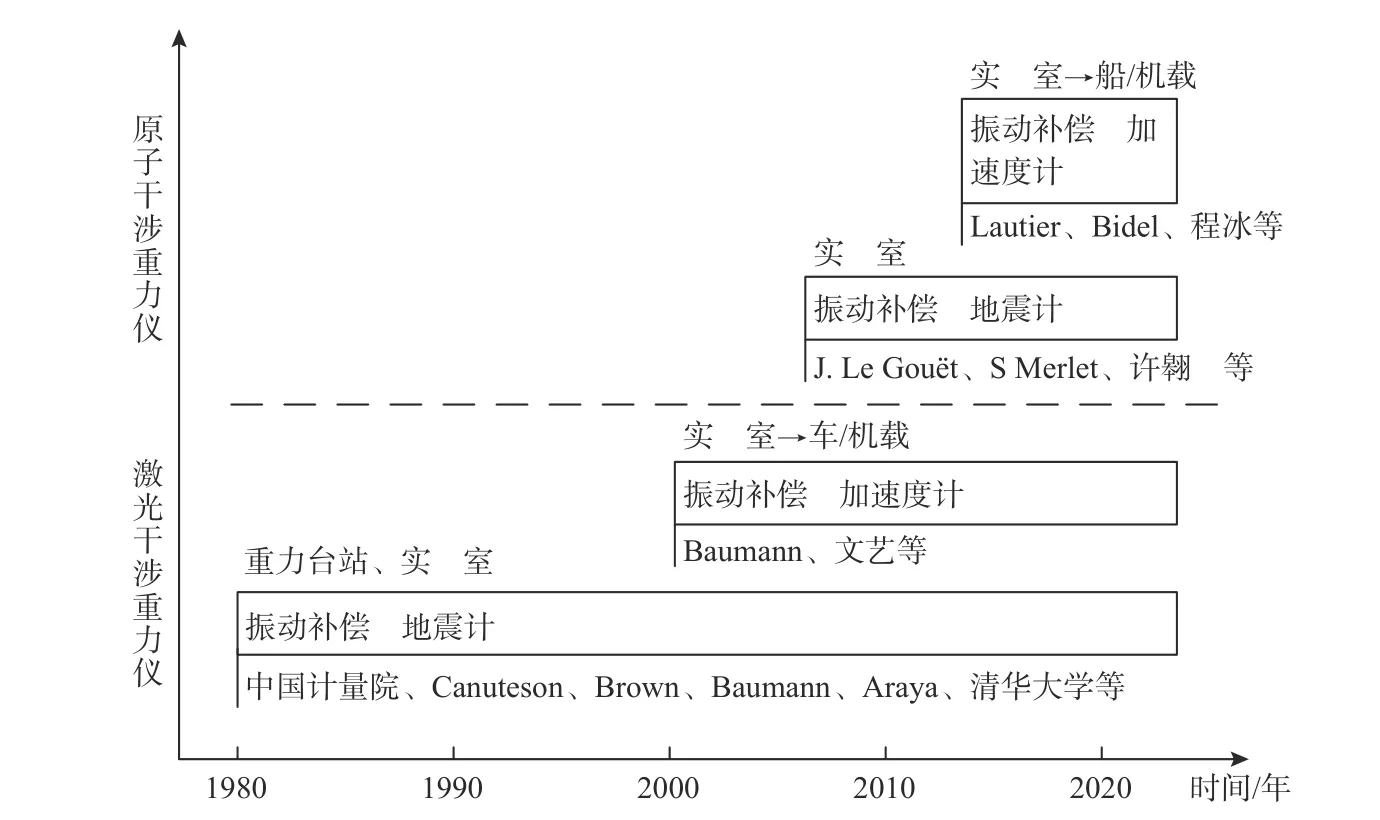
图20 应用于绝对重力测量的振动补偿技术发展情况Fig. 20 Development of vibration correction technology for absolute gravity measurement

一方面，要实现高精度的补偿效果，需要从传感器输出准确地还原出参考棱镜/反射镜的真实运动，这取决于两个关键因素：一个是尽可能准确地求解出传感器输出和参考棱镜/反射镜运动间的传递函数；另一个是传感器的性能需要确保输出信号足够准确. 对于外置传感器探测参考棱镜/反射镜运动的方式，可以通过在已有简化模型的基础上增加参数，以获得更接近真实传递函数的模型或者设计更加合理的滤波器来校正传感器信号，同时对传感器的选型（包括分辨率、带宽、测量范围等性能的选取）也非常重要；对于传感器将参考棱镜/反射镜作为敏感元件来直接获取其运动信号的方式，则需要进一步提高传感器的性能，包括分辨率、带宽、测量范围等（文艺等，2021）.

另一方面，补偿精度的提高往往伴随着补偿算法和传感器结构的复杂化，这有可能增加补偿所需的时间并降低补偿系统的抗干扰能力，从而限制在动态重力测量中的应用. 因此补偿精度和补偿速度、抗干扰能力之间的平衡将成为一个不可避免的问题. 对于不同应用场景中，补偿算法和传感器的选取将也将成为需要关注的关键问题.

总体而言，目前的振动补偿技术正从采用地震计进行较高精度的地面静态测量逐渐向采用加速度计进行动态测量发展，我国也在振动补偿领域取得了显著进展，包括清华大学、浙江工业大学、中国计量科学研究院等单位在内的多家研究机构提出了多种适用于激光干涉式绝对重力仪和原子干涉式绝对重力仪的振动补偿算法，补偿效果达到世界领先水平，有望在今后为实现小型化绝对重力仪的广泛应用提供有力的技术支撑.